基于尺度不变特征点匹配的太阳磁场图像配准与定位方法*

杨 盼，曾曙光，刘 锁，郑 胜，林钢华，何慧灵

(1. 三峡大学理学院，湖北 宜昌 443000；2. 中国科学院太阳活动重点实验室，北京 100012)

太阳磁场在太阳活动中扮演了极为关键的角色。为了预测耀斑和日冕物质抛射等太阳爆发活动，须监测从太阳光球到日冕的磁场和流场结构及其演化过程[1]。目前，国内外已经建有多个太阳磁场观测设备。如国内怀柔太阳观测基地(Huairou Solar Observing Station, HSOS)的35 cm太阳磁场望远镜(Solar Magnetic Field Telescope, SMFT)[2]、国外太阳动力天文台(Solar Dynamics Observatory, SDO)的日震及磁场成像仪(Helioseismic and Magnetic Imager, HMI)[3]等。不同太阳观测站间存在观测时间、观测范围、观测设备等差异，为了方便科学研究，提高太阳物理数据的使用效率，有必要找到不同观测站间太阳图像自动配准的方法。另外，当两观测设备的观测范围不同时，还需要实现 “小图像” 在 “大图像” 中的自动定位。例如，怀柔太阳观测基地的太阳磁场望远镜得到的是局部太阳磁场图像，然而，太阳动力学天文台的日震及磁场成像仪得到的是全日面太阳磁场图像。前者的观测范围远远小于后者，这就需要找到一种能够将局部太阳图像在全日面图像中快速定位的方法。

目前已有一些关于太阳图像配准方面的研究工作，如文[4]提出了基于修正矩的亚像素太阳图像配准算法，文[5]采用基于信息熵与尺度不变特征变换(Scale invariant feature Transform, SIFT)算法对太阳图像进行了配准。这些都是针对同一观测站的序列图像进行的，其成像设备位置固定，图像内容在短时间内变化较小，位移、旋转和仿射变换较少。不同太阳观测站的太阳图像由于在观测时间、观测范围、观测设备等方面存在较大差异，需要适应力更强的图像配准方法进行配准。已有的图像配准方法很多，如基于灰度的配准方法[6-7]、基于特征的配准方法[8-9]等等。基于灰度的配准方法具有精度高的优点，但计算复杂度高，且对目标的旋转、形变、遮挡以及灰度变化等很敏感。基于尺度不变特征点匹配的图像配准方法[10-11]计算量小，对灰度的变化、图像形变及遮掩等有较好的适应能力。太阳磁场图像含有许多内部结构，特征点较明显，本文提出了基于尺度不变特征点匹配的太阳磁场图像配准与定位方法，开展了怀柔太阳观测基地的局部太阳磁场图像在太阳动力天文台日震及磁场成像仪的全日面太阳磁场图像中自动配准与定位的研究，并做了检测实验证明方法的有效性。

1 算法原理

尺度不变特征点匹配算法对局部太阳图像在全日面太阳中自动配准与定位，主要包括尺度不变特征提取算法的特征点检测、特征点初步匹配、特征点精确匹配、图像变换矩阵求解4个步骤。

1.1 尺度不变特征变换特征点检测

1.1.1 尺度空间极值检测

尺度空间理论是检测不变特征的基础。文[12]证明了高斯卷积核是实现尺度变换的唯一变换核。

一幅二维图像在不同尺度下的尺度空间可以表示为图像与高斯核卷积：

L(x,y,σ)=G(x,y,σ)*I(x,y)，

(1)

其中，(x,y)为图像点的像素坐标；I(x,y)为图像灰度值；G(x,y,σ)为高斯核函数。

(2)

其中，σ为尺度空间因子，它是高斯正态分布的方差，反映了图像被平滑的程度；L(x,y,σ)为图像的尺度空间。

为高效地在尺度空间检测稳定的极值，文[10]使用尺度空间中高斯差分算子(Difference of Gaussian, DoG)的极值作为判断依据。高斯差分算子定义如下：

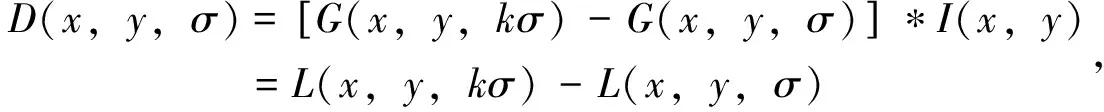
(3)

其中，k为相邻两个尺度空间的比例因子。

高斯差分算子局部极值的检测是将每个像素的高斯差分算子值跟同一尺度的周围邻域8个像素和相邻尺度对应位置的周围邻域9 × 2个像素总共26个像素进行比较。仅当被检测点的高斯差分算子值大于26个像素点或小于26个像素点时，才将其判断为极值点并保存，以进行后续计算。

1.1.2 确定关键点位置及尺度

通过拟合三维二次函数以精确确定关键点的位置和尺度，从而可得到原图像尺度不变特征提取算法的候选点集合。其中，对比度低的点对噪声比较敏感，而位于边缘上的点难以准确定位。为了确保尺度不变特征提取算法特征点的稳定性，须从尺度不变特征提取算法候选点集合将这两类点剔除。

1.1.3 关键点方向确定

通过确定关键点的方向，可以使特征描述符以与方向相关的方式构造，从而使算子具有旋转不变性。关键点的方向利用邻域像素的梯度分布特性确定。对每个高斯图像，每个点L(x,y)的梯度方向θ(x,y)可以由下式计算[10]：

(4)

1.1.4 特征向量生成

为了确保描述符的旋转不变性，首先需旋转坐标，保持坐标方向与极值点方向一致；然后将平面内可能分布的360°梯度方向划为8个方向范围，每个方向范围各包含45°。在子区域为4 × 4的情况下，共计有4 × 4 × 8=128个数据，即生成128维描述符。方向与信息联合不仅增强了抗噪性，还消除了尺度变化、旋转和变形的影响[5,10]。

1.2 特征点初步匹配

完成特征点检测后，可利用寻找同名点的方法对两幅图像特征点进行粗匹配[5,10]。以欧式距离d作为图像间的相似性度量以确定同名点。欧式距离二维表示为

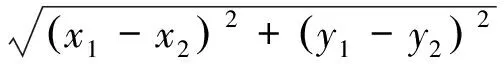
(5)

首先在待配准图像中找出两个与参考图像中对应某极值点的欧氏距离最短的点；然后以两个值中小的值作为分子，大的值作为分母，若该分数值在给定的阈值范围内，那么建立对应点的同名点关系，称为匹配点。阈值的选取将直接影响同名点的数量。阈值越大，获得的匹配点越多，可能的误匹配也越多；阈值过小时，匹配点会很少。大量实验表明，阈值在0.4～0.6之间最佳[5]。

1.3 特征点精确匹配及变换矩阵求解

在完成特征点粗匹配后，可利用随机抽样一致性算法[9]消除错误的匹配点，从而提高配准精度。随机抽样一致性算法，可以在一组包含 “外点” 的数据集中，采用不断迭代的方法，寻找最优参数模型，不符合最优模型的点，被定义为 “外点”。该算法最早由文[9]提出，在图像配准以及拼接上得到广泛应用。

一般地，两幅图像间的变换可以由变换矩阵表示[13]：

(6)

其中，(x′,y′)和(x,y)分别为两幅图像中对应点的像素坐标；hi(i=0, 1, 2, ..., 7)为变换矩阵的8个未知系数。

随机抽样一致性算法可对特征点进行精确匹配并求变换矩阵。首先随机选择4组对应点组成一个随机样本并计算变换矩阵H，对假设的每组对应计算距离d，计算与H一致的内点数，选择有最多内点数的H，在数目相等时，选择内点标准方差最小的那个解[13]。最后根据图像间变换矩阵H，可以计算出局部太阳图像的4个顶点及中心点在全日面图像中的像素坐标，从而完成局部太阳图像在全日面太阳图像中的配准与定位。

2 算法设计及实验分析

2.1 算法设计

基于尺度不变特征匹配的太阳磁场图像配准与定位方法流程如下：

(1)对图像进行预处理，包括降采样、黑白反相、对比度增强等，对图像降采样到1 024 × 1 024左右；

(2)通过尺度不变特征提取算法提取图像特征点；

(3)采用寻找同名点的方法对两幅图像特征点进行粗匹配；

(4)利用随机抽样一致性算法去除错误的匹配点，并估计两幅图像之间的最佳变换矩阵H；

(5)根据仿射变换矩阵，实现局部太阳图像在全日面太阳图像中的初步定位；

(6)利用初步定位的图像区域和怀柔局部图像进行精确配准。

算法的具体流程如图1。

图1 太阳图像配准与定位流程图
Fig.1 Flow chart of solar image registration and positioning

2.2 实验结果与分析

2.2.1 不同观测站太阳磁场图像的配准与定位

以怀柔太阳观测基地的局部太阳磁场图像在SDO/HMI的全日面太阳磁场图像中的自动匹配与定位展开实验。图2给出了原始的全日面太阳图像及局部太阳图像。其中，图2(a)给出日震及磁场成像仪[3]得到的全日面太阳磁场图像，拍摄时间2012年11月12日05时48分00秒。图2(b)给出35 cm太阳磁场望远镜[2]得到的局部太阳磁场图像，拍摄时间2012年11月12日05时55分34秒。两者的拍摄时间非常接近。值得指出的是，两者的观测范围和分辨率有很大差异。怀柔太阳观测基地的局部太阳图像仅仅是全日面太阳图像中很小的一部分。全日面图像的尺度是4 096 × 4 096，怀柔站局部图像的尺度830 × 992。

图2 原始的太阳磁场图像
Fig.2 Original solar magnetic field image (Full-disk solar magnetic field image in (a) and local solar magnetic field image (in(b)))

图2中两幅图像的对比度不够。在进行后续的图像配准前，有必要通过对比度增强等对两幅图像进行预处理。另外，由于日震及磁场成像仪的全日面图像分辨率太高，为了提高配准速度，先做降采样处理，将尺度从4 096 × 4 096降低到1 024 × 1 024。最后，部分日震及磁场成像仪的全日面太阳磁场图像的正负极性与怀柔观测站的相反，因此要做黑白反相处理。经过降采样、黑白反相及对比度增强处理后的全日面太阳磁场图像如图3(a)。经过对比度增强后的局部太阳图像如图3(b)。对比图2(b)和图3(b)可以发现，预处理后的太阳图像比原始图像更加清晰，这有利于后续的特征提取与图像配准。

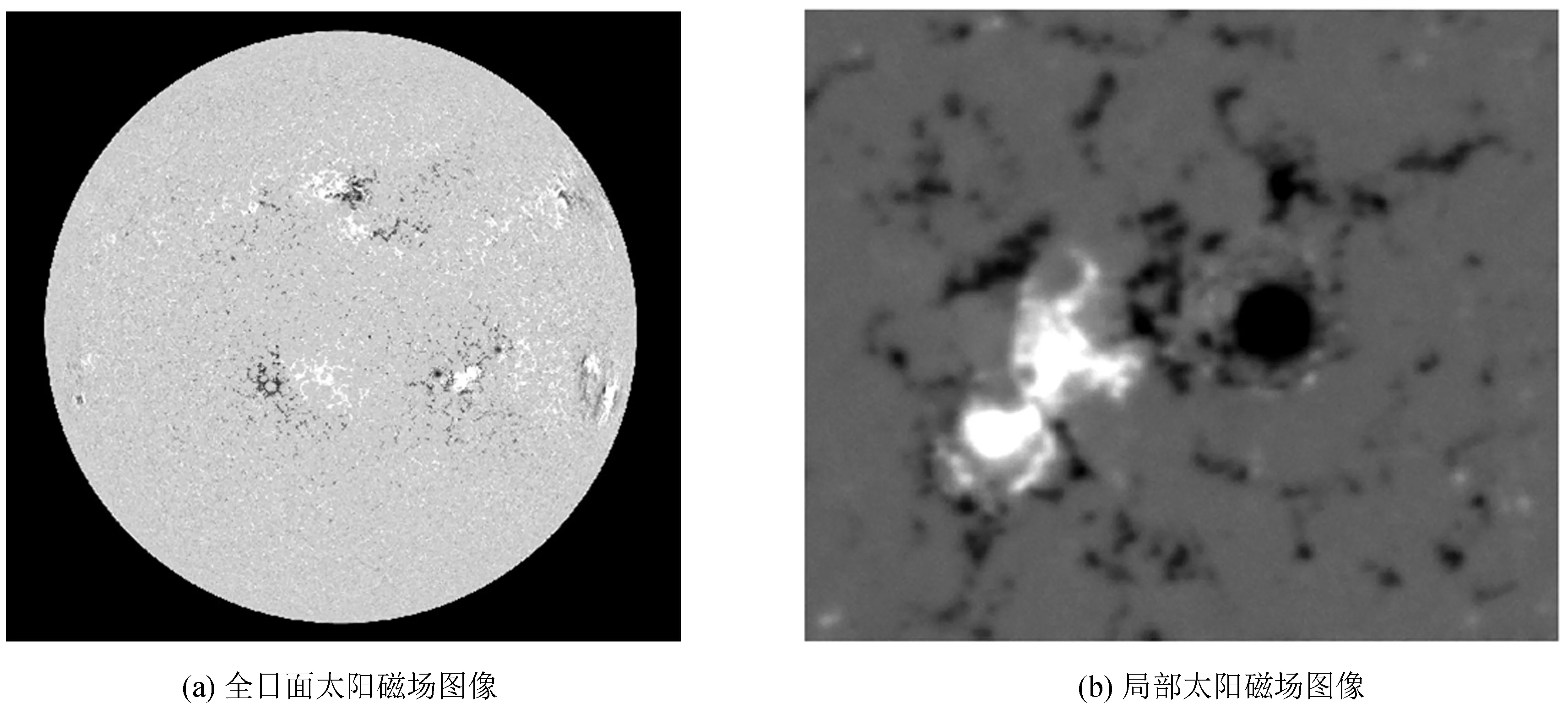
图3 经过预处理后的太阳磁场图像
Fig.3 Full-disk solar magnetic field image (in(a)) and local solar magnetic field image (in(b)) after pre-treatment

随后，采用尺度不变特征提取算法提取图像特征点。图4给出了经过预处理后的局部太阳图像的尺度不变特征检测结果。一共检测到了204个尺度不变特征点。由图4可见，这些特征点较好地代表了局部太阳图像的特征。

在对图3中的两幅图像进行尺度不变特征检测后，需要将两幅图的特征点配准。图3中的全日面图像一共检测到了3 447个尺度不变特征点，局部太阳图像一共检测到了204个尺度不变特征点。接下来，采用寻找同名点的方法以及随机抽样一致性算法找出两幅图中相互配准的特征点对。如图5，一共找到了20个相互配准的特征点对(图中用红色直线连接)。根据这些配准特征点对，可初步估计两幅图像之间的变换矩阵H1[13]，具体如(7)式：

(7)

根据变换矩阵H1可以计算局部图像的4个顶点及中心点在全日面图像中的像素位置，从而完成了局部图像在全日面图像中的粗定位(图5)。

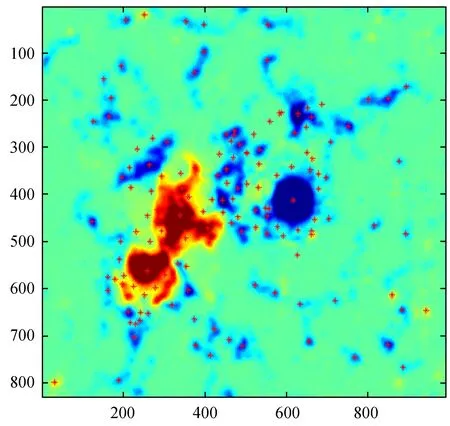
图4 经过预处理后的局部太阳图像的尺度不变特征检测

Fig.4 Scale-invariant feature detection of localized solar image after pre-treatment

图5 局部图像在全日面图像中的配准与定位
Fig.5 Registration and positioning of local image in full-disk solar image

对日震及磁场成像仪全日面图像进行降采样处理可以大大提高计算速度，但同时也会降低匹配与定位精度。为此，将日震及磁场成像仪全日面原始图像中绿色四边形对应的最小外接矩形区域(见图5)与怀柔局部太阳图像做精确匹配，即可确定局部太阳图像在全日面图像中的精确范围。精确匹配后的结果如图6，一共找到了25个相互配准的特征点对(图中用红色直线连接)。根据这些配准特征点对，可估计两幅图像之间的最佳变换矩阵H2，具体如(8)式：

(8)

由变换矩阵H2可以看出，两图像间主要存在缩放、旋转、平移等几何变换，不存在透射变换，且可以计算局部图像的4个顶点在全日面图像中的精确位置分别为(2 909, 2 704)、(2 371, 2 484)、(2 560, 2 045)、(3 097, 2 265)(图6中用绿色四边形标出)，从而完成了局部图像在全日面图像中的精确定位。另外，还可以计算局部太阳图像相对于全日面图像的旋转角度约为157.9°(顺时针)；水平方向放大比例为1.71，垂直方向放大比例为1.74。

图6 局部图像在全日面图像中的精确配准与定位
Fig.6 Accurate registration and positioning of local image in full-disk solar image

图7给出了局部放大后的全日面太阳图像(图7(a))与经过变换矩阵H变换后的局部太阳图像(图7(b))。由图可见，两图的形状、角度等基本一致，但细节方面略有差异。两图形状、角度等基本一致证明了本文算法的准确性。两图细节方面略有差异是因为两者是由不同观测站得到的，在观测时间、望远镜参数等方面存在差异所致。但这些细微的差异不会影响局部太阳图像在全日面图像中的配准与定位。

图7 全日面太阳磁场图像与经过变换后的局部太阳磁场图像
Fig.7 Full-disk solar magnetic field image (in(a)) and transformed local solar magnetic field image (in(b))

2.2.2 不同时间段的匹配结果

为了验证算法的有效性，对71组不同时段的太阳图像进行配准，并给出相应的配准点对数与正确配准点对数，结果如图8。其中，红色实线圆圈为实际的配准点对数，绿色虚线点为正确配准的点对数，蓝色虚线五角星为配准的正确率(即正确配准的点对数与实际配准的点对数之比)，全日面图像分辨率均为1 024 × 1 024。由图8可以看出，大部分情况下正确配准的点对数与实际的配准点对数相等，即配准准确率为100%；少数情况下正确配准的点对数小于实际的配准点对数，即存在一定的错误配准。出现错误配准的原因在于：怀柔局部太阳图像和日震及磁场成像仪全日面太阳图像，一个是地面拍摄的，一个是空间拍摄的。在大气湍流等干扰下，怀柔局部太阳图像会变得模糊，尺度不变特征变换算法能检测到的特征点减少，进而导致配准点对数和配准准确率的下降。图9给出了局部太阳图像较模糊时的配准情况，当怀柔局部太阳图像较为模糊时，配准点对数与配准准确率较低。

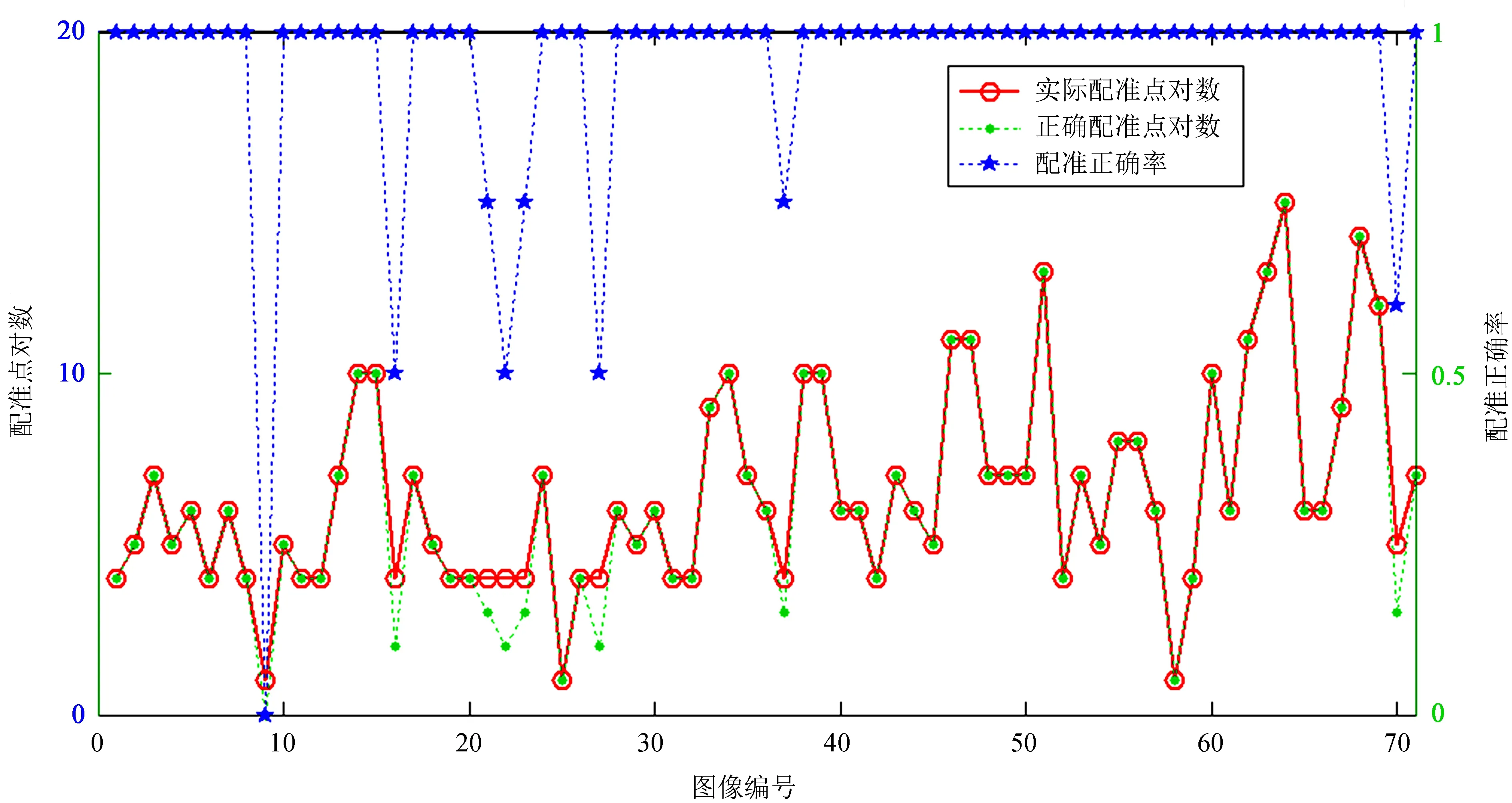
图8 不同时间太阳磁场图像的配准情况
Fig.8 The registration of the solar magnetic field image at different time

图9 局部太阳磁场图像较模糊时的配准情况
Fig.9 Registration results of a blurry local solar magnetic field image

2.2.3 仿射变换对太阳磁场图像配准结果的影响

不同观测站的太阳磁场图像间除了常见的缩放、旋转和平移变换，很多情况下还存在比较明显的仿射变换。本节研究仿射变换对太阳磁场图像配准结果的影响，通过定量分析并计算配准实验的误差。从原始日震及磁场成像仪全日面图像中(图2(a))抠出一块矩形子图像。然后，将矩形子图像进行一定的仿射变换，最后，将仿射变换后的子图像与降采样后的全日面图像(图3(a))做配准，将变换矩阵计算得到的子图像在全日面图像中的位置与子图像在全日面图像中的已知位置相减，即可准确地计算配准误差。配准误差η定义为

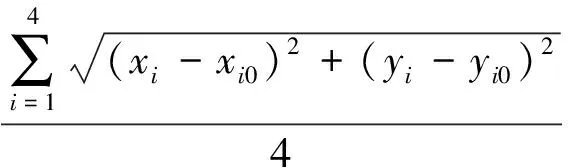
(9)

其中，(xi0,yi0)和(xi,yi)分别为子图像的4个顶点在全日面图像中的已知位置和经过变换矩阵预测的位置。

仿射变换包含平移、旋转、缩放、错切等变换。图10给出了缩放为0.6倍的情况下，配准误差(单位：像素)随错切系数和旋转角度的变化情况。由图10可以看出，当错切系数较小时，配准误差较小，而当错切系数增大到一定程度如超过0.3后，配准误差将迅速增大；旋转角度对配准结果影响较小。图11给出了旋转角度为45°的情况下，配准误差随错切系数和缩放系数的变化情况。由图11可以看出，放大2倍以内，对配准误差的影响较小，超出此范围后配准误差将明显增大。这是因为缩小变换需要丢弃一些图像信息，而放大变换则需要插值来增大图像。当缩小导致丢弃的信息太多或放大插值的信息太多时对特征点的检测与配准造成影响。综上所述，本文采用的尺度不变特征变换配准算法对旋转、缩放、错切变换等均具有一定的鲁棒性。为了更好地反映仿射变换对配准精度的影响，本节的结果都是通过初步定位得到的，通过精确定位可以大大减小配准误差。

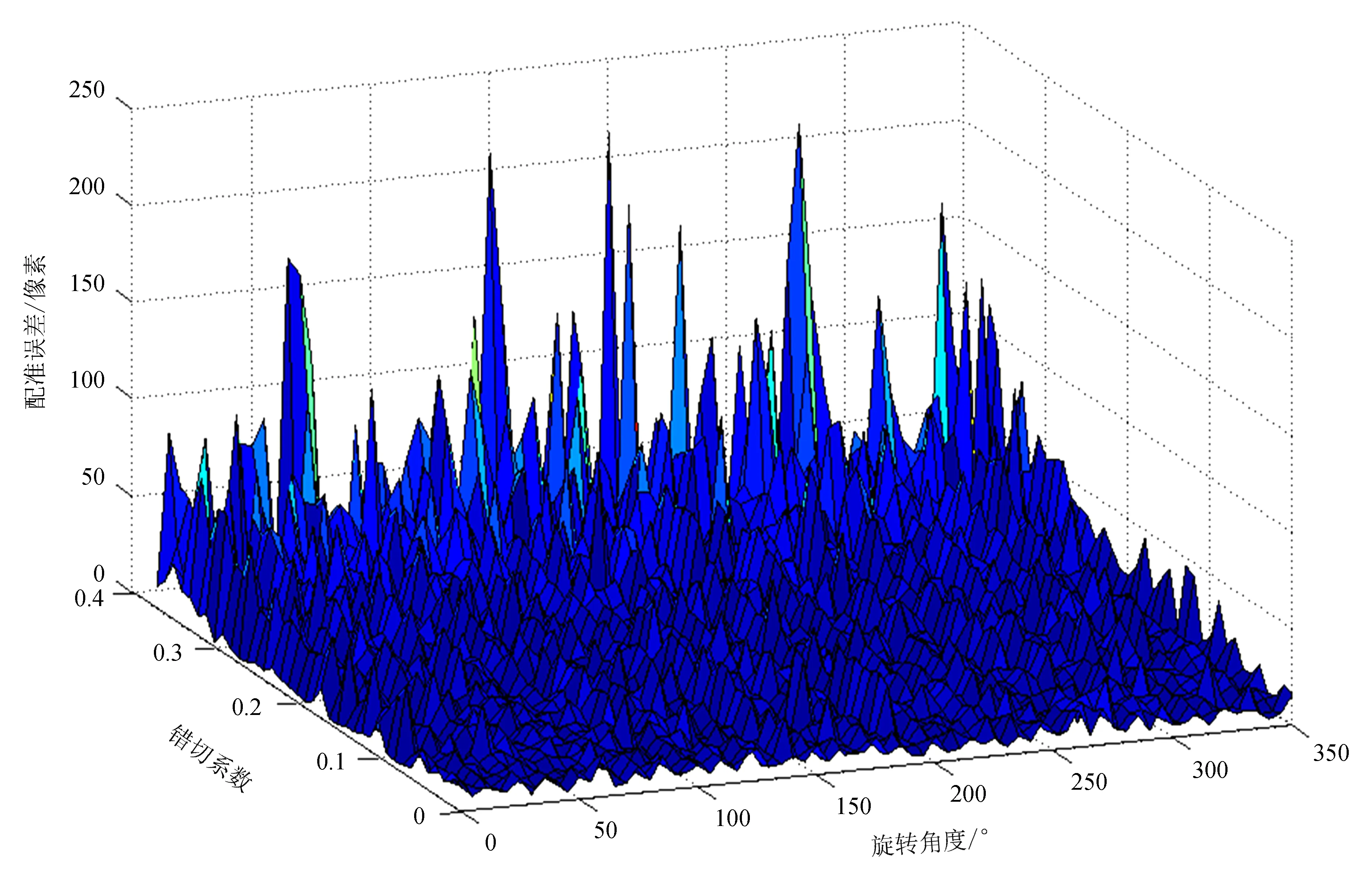
图10 配准误差随错切系数和旋转角度的变化
Fig.10 The change of registration error varies with the shear factor and the rotation angle

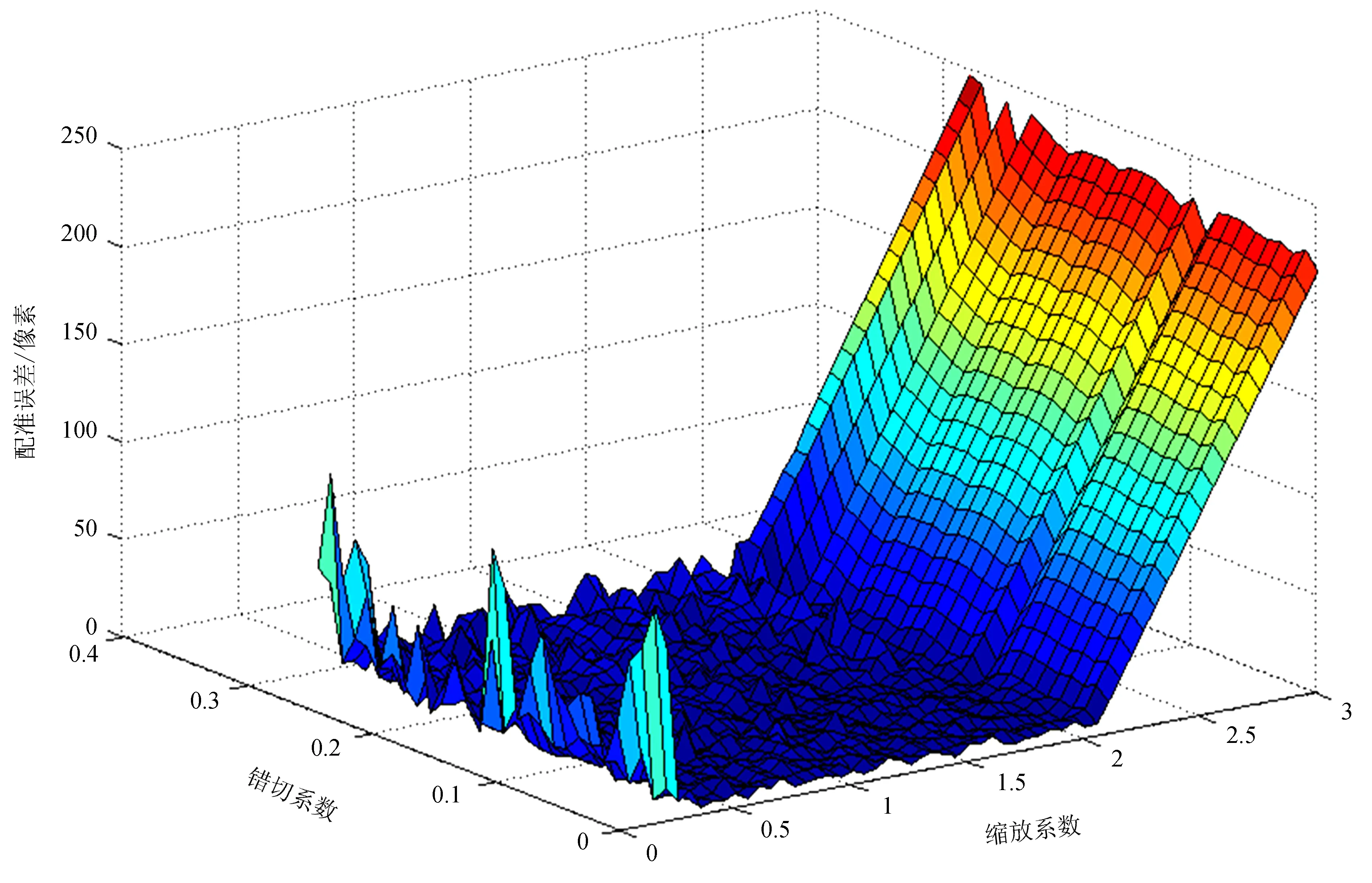
图11 配准误差随错切系数和缩放系数的变化
Fig.11 The change of registration error varies with the shear factor and zoom factor

3 结 论

采用基于尺度不变特征点匹配的方法对怀柔观测站的局部太阳磁场图像在太阳动力天文台日震及磁场成像仪的全日面图像中的配准与定位问题进行了研究，结果表明，该算法对光照、旋转、尺度缩放等有很强的鲁棒性，对不同观测站得到的具有不同观测条件、不同观测尺度等的太阳磁场图像的配准有效且提高了太阳物理数据的使用效率。

[1] 刘忠, 邓元勇, 季海生, 等. 中国地基大太阳望远镜[J]. 中国科学: 物理学 力学 天文学, 2012, 42(12): 1282-1291.

Liu Zhong, Deng Yuanyong, Ji Haisheng, et al. China Large Earth-based Solar Telescope[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2012, 42(12): 1282-1291.

[2] 艾国祥, 胡岳风. 太阳磁场望远镜的工作原理[J]. 天文学报, 1986(2): 91-98.

Ai Guoxiang, Hu Yuefeng. On principle of solor magnetic field telescope[J]. Acta Astronomica Sinica, 1986(2): 91-98.

[3] Schou J, Scherrer P H, Bush R I, et al. Design and ground calibration of the Helioseismic and Magnetic Imager(HMI) Instrument on the Solar Dynamics Observatory (SDO) [J]. Solar Physics, 2012, 275(1-2): 229-259.

[4] 陈洁. 太阳图像的亚像素配准算法的研究与应用[D]. 昆明: 昆明理工大学, 2013.

[5] 岳昕, 尚振宏, 强振平, 等. 基于信息熵与SIFT算法的天文图像配准[J]. 计算机科学, 2015, 42(6): 57-60.

Yue Xin, Shang Zhenhong, Qiang Zhenping, et al. Astronomical image registration combining information entropy and SIFT algorithm[J]. Computer Science, 2015, 42(6): 57-60.

[6] Goshtasby A, Stockman G C, Page C V. A region-based approach to digital image registration with subpixel accuracy[J]. IEEE Transactions on Geoscience & Remote Sensing, 1986, GE-24(3): 390-399.

[7] Pratt W K. Correlation techniques of image registration[J]. IEEE Transactions on Aerospace & Electronic Systems, 1974, AES-10(3): 353-358.

[8] Bouchiha R, Besbes K. Automatic remote-sensing image registration using SURF[C]// The 3rd International Conference on Machine Vision. 2013: 406-410.

[9] Fischler M A, Bolles R C. Random sample consensus: a paradigm for model fitting with a pplications to image analysis and automated cartography[J]. Readings in Computer Vision, 1987, 24(6): 726-740.

[10]Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[11]Lowe D G. Object recognition from local scale-invariant features[C]// The Proceedings of the Seventh IEEE International Conference on Computer Vision. 1999.

[12]Koenderink J J. The structure of images[J]. Biological Cybernetics, 1984, 50(5): 363-370.

[13]赵小川. 现代数字图像处理技术提高及应用案例详解[M]. 北京: 北京航空航天大学出版社, 2012.