足迹不同部位测量值与身高之间的相关性

史力民 朱玉婷 班茂森

（1 中国刑事警察学院痕迹检验技术系 辽宁 沈阳 110035；2 公安部物证鉴定中心 北京 100038）

现已开展了诸多关于利用足迹测量值估算身高的研究[1]。利用现场足迹分析身高，缩小侦查范围，为侦查提供线索和方向，是足迹检验技术在侦查破案中的重要作用之一。实际工作中常用“身高=赤足足迹长×7”[2]公式来推算身高，然而该公式有一定误差，鉴于足长与身高之间的相关性强弱与地理位置有关，生活在南方或北方的青年人足长与身高的比例不同[3]，为减少地区差异带来的影响，本文选取70名河南籍青年人，通过测量其左右足且多个足迹的不同长度与宽度，利用SPSS软件进行统计分析，比较不同测量值与身高之间的相关系数，并得出对应的回归方程，比较误差范围与比率，对利用赤足足迹长进行身高分析，得出新的评估方法，为利用赤足残缺足迹进行身高分析提供依据。

1 实验部分

1.1 收集样本

实验受试者是70名河南人，其中58名男性，12名女性，年龄集中在18～25岁之间。所有受试者均健康且脚无明显畸形。对每个受试者测量身高，并捺印赤足足迹。

1.1.1 身高的测量

身高值是头顶部与地板的垂直距离（在弗兰克福水平面上头的最高点）[4]。被测量人需光脚垂直站立，并且头上不带任何饰物。要求被测量人靠着墙垂直站立，并且手悬空下垂，双脚平行或稍微分展，并且头部必须在弗兰克福水平面。身高测量时无压力施加，为接触测量。以厘米为计量，精确到小数点后一位的标准方法记录身高值。

1.1.2 足迹的捺印

根据Cummins和Midlo所说方法[5]，让沾有油墨的足通过行走将足迹遗留在纸张上来收集足迹。脚离开取样纸前，用铅笔尖在纸上依据解剖学中脚骨的形态结构标志，标记出脚的各个标记点：拇趾前缘最突出点；跖内缘最突出点；跖外缘最突出点；跟内缘最突出点；跟外缘最突出点；跟后缘最突出点。

1.2 选取数据

每个受试者左右足分别测量共7个值（图1）。并根据Robbins[6]和Krishan[7]的方法，以足迹中心线为纵轴，以垂直于纵轴的后跟切线确定为基线。每个足迹分别测量以下值：L1拇趾前缘到跖内缘的距离；L2拇趾前缘到跖外缘的距离；L3跖内缘到跟后缘的距离；L4跖外缘到跟后缘的距离；L5赤足足迹长；L6足跖宽；L7足跟宽。

图1

1.3 测量数据

用数码分规对样本进行测量。每个受试者左右足分别测量7个值，并将身高（S）和这14个值录入表格，以备后期的软件处理。

2 数据分析

2.1 数据预处理

用SPSS统计分析软件对足迹测量值进行分析，先进行预处理，剔除异常数据，利用有效数据，求出身高、左右足上分别7个测量值的极大值、极小值、均值、标准差和方差，得出表1。可以看出，本次参加实验的受试者，身高分布在160.5～186.6cm之间，分布广泛，离散程度大。从左右足共14个测量值的标准差和方差可以看出，左右足长（LL5、RL5）的离散程度最大，其次为右左足跖内缘到跟后缘的距离（RL3、LL3），其他测量值的方差则相对较小。

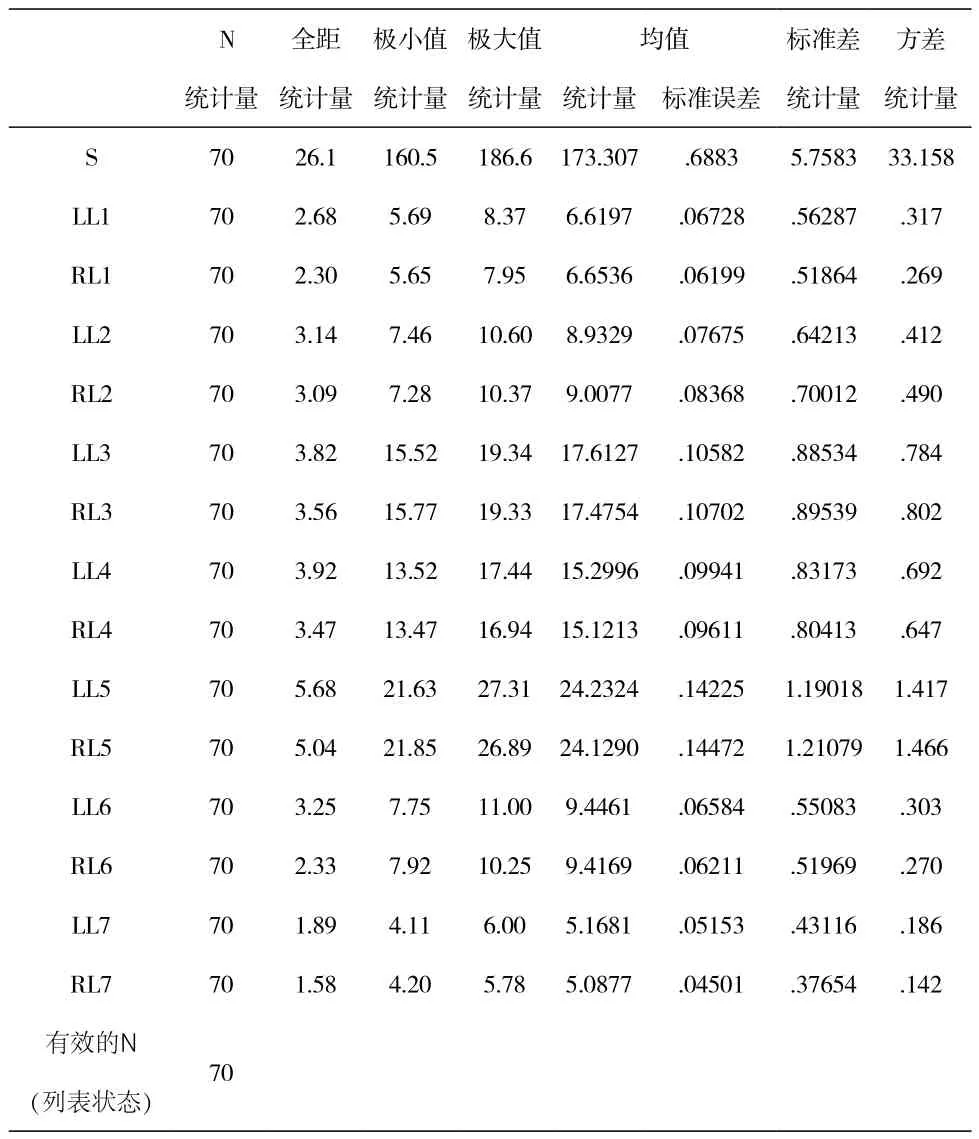
表1 描述统计量 （cm）

为比较左右双足相关测量值之间是否存在差异，对14个测量值进行配对样本T检验，得出表2。可以看出，在拇趾前缘到跖内缘的距离（L1）与拇趾前缘到跖外缘的距离（L2）上，左足稍微小于右足，除此之外其他测量值均是右足相对稍大。跖外缘到跟后缘的距离（L4）在左右足上的差异最大，跖内缘到跟后缘的距离（L3）与足长（L5）在左右足上的差异相对其他测量值稍大。在显著性水平α=0.05的水平上，跖内缘到跟后缘的距离（L3）、跖外缘到跟后缘的距离（L4）和足跟宽（L7），在左右足上有显著差异。在显著性水平α=0.01水平上，跖内缘到跟后缘的距离（L3）和跖外缘到跟后缘的距离（L4），在左右足上测量值差异非常显著，其他测量值在两个水平下差异均不显著。

表2 成对样本检验 （cm）

2.2 相关性分析

利用SPSS的双变量相关分析功能分析身高与不同测量值之间的相关性，得出不同测量值与身高之间的Pearson相关系数，如表3，并比较不同测量值与身高之间的相关系数和显著性。

表3 不同测量值与身高之间的Pearson相关系数

从表3可以看出，所有足迹测量值与身高的相关系数的范围从0.450到0.680不等。其中右足足长（RL5）与身高之间的相关系数最大（r=0.680），其次为左足足长（LL5）与身高的相关系数（r=0.646）和右足跖内缘到跟后缘的距离RL3（r=0.628）。相比之下，LL3与身高的相关系数（r=0.577）则略小，这与表2所示左右足L3测量值存在显著差异相一致。左足拇趾前缘到跖外缘的距离（LL2）与身高之间的相关系数最小（r=0.450）。很明显，所有足迹测量值与身高均在α=0.01水平上显著相关。

2.3 回归分析

通过不同足迹测量值分别与身高建立一元线性回归方程，并得出其标准估计的误差，如表4。

表4 不同足迹测量值与身高（S）之间的一元回归分析 （cm）

表4列出了不同测量值与身高之间的一元回归方程，将所得足迹测量值代入对应的方程即可推算出理论的身高，例如测得已知RL3=17.12cm，代入RL3与身高的回归方程，则估算的身高S=102.676+4.042×17.12=171.87504cm。此外，从表4可以看出，在不同测量值与身高之间的一元回归方程中，RL5推算的标准估计的误差最小（4.2523），其次为LL5（4.4264）、RL3（4.5118）和LL7（4.5451）。

为提高身高分析的准确率，现选取表4中标准估计的误差小于5对应的足迹测量值，即RL2、LL3、RL3、LL4、RL4、LL5、RL5、RL6、LL7这9个测量值，在左足和右足上分别与身高建立二元一次回归方程，并得出其标准估计的误差，如表5。

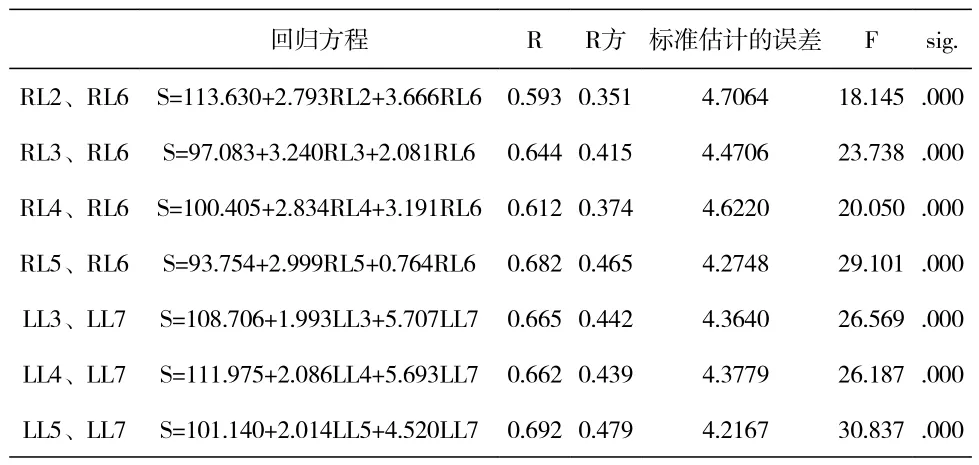
表5 不同足迹测量值与身高（S）之间的二元回归分析 （cm）

表5列出了经选取过的足迹测量值与身高之间的二元一次回归方程，将所得足迹测量值带入对应的方程即可推算出理论的身高，例如测得已知RL3=17.12cm，RL6=9.07cm，代入RL3、RL6与身高的回归方程，则估算的身高S=97.083+3.240×17.12+2.081×9.07=171.42647cm。从表5可以看出，在不同测量值与身高之间的二元一次回归方程中，LL5、LL7推算的标准估计的误差最小（4.2167），其次为RL5、RL6（4.2748），LL3、LL7（4.3640），LL4、LL7（4.3779）和RL3、RL6（4.4706）。比较表4和表5，发现利用相同足迹测量值与身高分别建立的一元回归与二元回归之间，二元回归方程对应的标准估计的误差均较小。

2.4 误差与准确率

表6是一元回归分析中，不同测量值的身高估算值与实际身高在不同误差范围内的样本数量和比率。从表6可以看出，误差在1cm范围内时，不同测量值的样本比率均超过10.00%，其中LL3、RL4、LL5、RL6、LL7和RL7的比率均在15.00%以上。误差在2cm时，RL6和LL6最高为37.14%，在RL4（34.29%）之后，是RL3（32.86%）。误差在3cm时，LL7最高，为52.86%，其次为RL3和RL4，均是48.57%。误差在4cm时，RL3最高，为65.71%，而RL5仅为60.00%。误差在5cm时，LL7和RL5是最高的，为75.71%，其后为LL5（74.29%），RL2、RL3和RL6相同，均为71.43%。

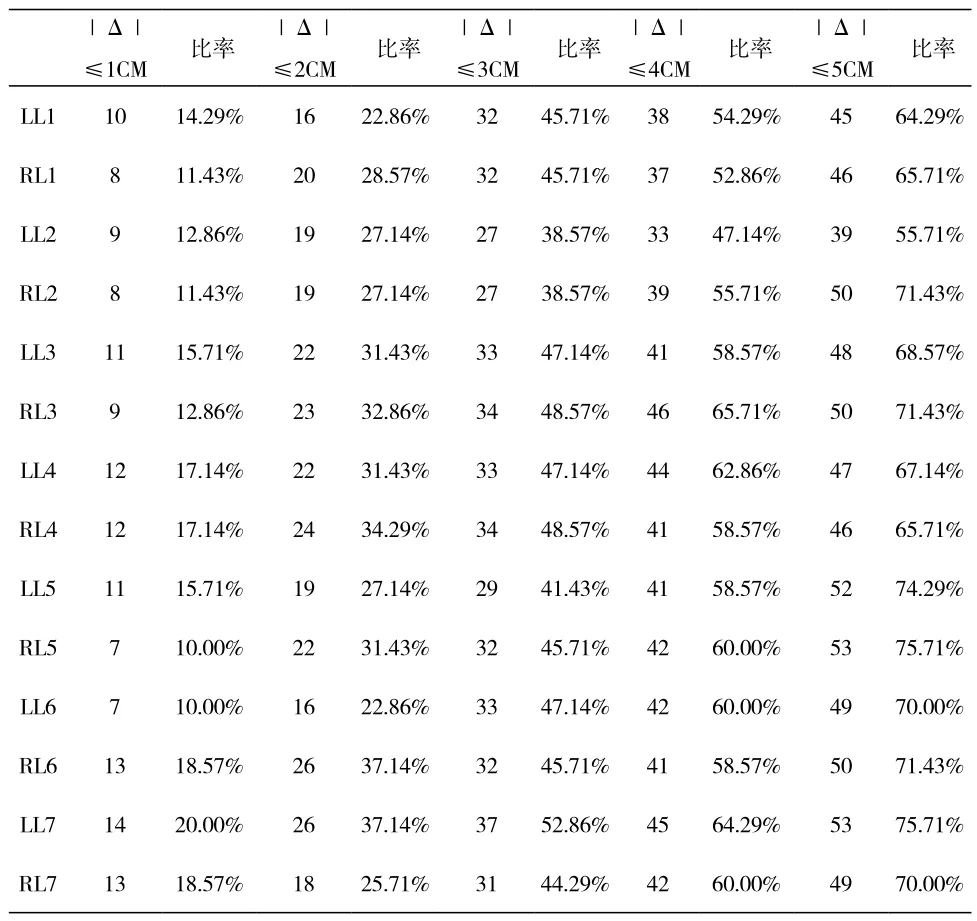
表6 一元回归分析不同测量值不同误差范围与其比率

由于RL3与身高之间的相关性及利用RL3推算身高标准估计的误差均仅次于RL5和LL5，着重比较L3和L5在不同误差范围内的准确率。在1cm误差内时，左右足的L3比率均稍微大于L5；在2cm误差内时，左右足的L3仍均略大于L5；在3cm误差内时，左右足L3均大于L5；在4cm误差内时，仅RL3大于RL5，LL3与LL5则持平；然而在5cm误差内时，L5均大于L3。

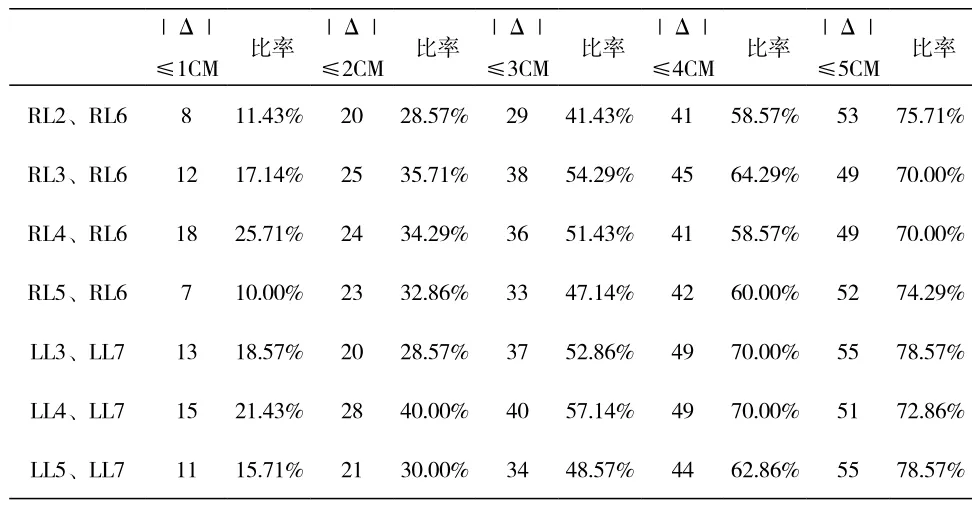
表7 二元回归分析不同测量值不同误差范围与其比率

表7是二元一次回归分析分析中，经选取过的不同测量值的身高估算值与实际身高在不同误差范围内的样本数量和比率。从此表可以看出，误差在1cm范围内时，不同测量值的样本比率均超过10.00%，有的甚至达到了25.71%（RL4、RL6）。误差在2cm时，LL4、LL7最高为40.00%，在RL3、RL6（35.71%）之后，是RL4、RL6（34.29%）。误差在3cm时，LL4、LL7最高，为57.14%，其次为RL3、RL6（54.29%），LL3、LL7（52.86%）。误差在4cm时，LL3、LL7，LL4、LL7并列最高，为70.00%，其次为RL3、RL6（64.29%），而RL5、RL6仅为60.00%。误差在5cm时，所有比率均在70.00%以上，其中LL3、LL7，LL5、LL7一样高，为78.57%，其后为RL2、RL6（75.71%），RL5、RL6（74.29%）。

在右足上，着重比较RL3、RL6与RL5、RL6，可以看出，在误差分别为1cm、2cm、3cm、4cm上时，RL3、RL6二元回归分析身高的准确率均大于RL5、RL6；与之相反，在误差为5cm时稍小于RL5、RL6。在左足上，比较LL3、LL7与LL5、LL7，发现误差在1cm与2cm时，两者并无明显差别，误差在3cm与4cm时，LL3、LL7对应比率稍微高于LL5、LL7，在5cm误差时，两者比率一样。

3 实验结果分析与讨论

结果表明，本文测量的多个赤足足迹测量值均与身高有较显著的相关性，并且右左足跖内缘到跟后缘的距离（RL3、LL3）与右左足长（RL5、LL5）在离散程度、身高的Pearson相关性和推算身高回归方程的误差方面均有相似的价值。对右足迹研究发现：在误差小于4cm时，利用足跖内缘到跟后缘的距离（RL3）通过一元回归方程（见表4，S=102.676+4.042RL3）分析身高比利用足长（L5）推算身高有更高的准确率，且误差越小准确率更高；相比之下，具有更高准确率的二元一次回归分析中，误差小于4cm时，利用足跖内缘到跟后缘的距离与足跖宽（RL3、RL6）（见表5，S=97.083+3.240RL3+2.081RL6）比足长与足跖宽（R L 5、R L 6）（见表5，S=93.754+2.999RL5+0.764RL6）分析身高更准确。对左足迹研究发现：利用足跖内缘到跟后缘的距离与足跟宽（LL3、LL7）（见表5，S=108.706+1.993LL3+5.707LL7）比足长与足跟宽（L L 5、L L 7）（见表5，S=101.140+2.014LL5+4.520LL7）分析身高误差并无太大区别。

4 结论

本文对利用赤足足迹进行身高分析时提出了新的评估方法，即足趾残缺不全无法确定赤足长时，右足迹可用足跖内缘到跟后缘的距离（RL3）一元回归分析身高，也可用足跖内缘到跟后缘的距离与足跖宽（RL3、RL6）二元回归分析身高；而左足迹可用足跖内缘到跟后缘的距离与足跟宽（LL3、LL7）二元回归分析身高。本方法与传统利用足迹长分析身高公式的分析结果比较，一定程度上提高了足迹分析身高的准确性，同时也丰富了利用赤足残缺足迹进行身高分析的方法。

[1]史力民.足迹学[M].北京:中国人民公安大学出版社,2007:240-246.

[2]吴旭芒,高以群.足迹学[M].北京:警官教育出版社,1995:239-246.

[3]李纪江,蔡睿.地质划分与体制地域分布特征现状综述[J].四川体育科学,2010(2):79-89.

[4]Kewal Krishan,Tanuj Kanchan.Heel-Ball (HB) Index:Sexual Dimorphism of a New Index from Foot Dimensions[J]. Forensic Sciences,2012(1):172-175.

[5]Cummins H,Midlo M.Finger Prints,Palms and Soles:An Introduction to Dermatoglyphics[M].New York:Dover Publications,1961:172-184.

[6]Robbins L M.F ootprints:Collection,Analysis and Interpretation[M].Springfield, IL:Charles C.Thomas,USA,1985:122-132.

[7]Krishan K. Estimation of stature from footprints and foot outline dimensions in G ujjars of North India[J].Forensic Science,2007(2-3):93-101.