利用城市监控卡口网络的最优追踪路径规划

孙 鹏 董 帅 郎宇博 王大宇 单大国

（1 中国刑事警察学院声像资料检验技术系 辽宁 沈阳 110035；2 江西省经济犯罪侦查与防控技术协同创新中心 江西 南昌 330103；3 防城港市公安局物证鉴定中心 广西 防城港 538000）

1 引言

随着全球城市化进程的加快，城市安全问题变得越来越严重[1]。为了维护社会稳定，许多城市已经建立了城市监控卡口网络系统。现阶段城市监控卡口的主要任务只是简单的对道路上机动车辆进行测速和了解路面状况，在维护城市安全方面城市监控卡口的利用效率比较低，因此，如何高效的利用城市监控卡口网络维护城市安全成为公安机关十分关注的问题。当侦查员发现犯罪嫌疑人行踪时，公安人员要制定计划对犯罪嫌疑人进行抓捕，对于追踪犯罪嫌疑人的路径基本上是侦查员凭借自己的主观意志判断没有任何科学依据，这种不科学性就可能导致犯罪嫌疑人有充分的时间进行逃窜或者二次作案。针对这个问题并结合视频侦查实际工作需要，本文提出了一种利用城市监控卡口网络寻找最优路径追踪犯罪嫌疑人的视频侦查方法。

近些年国内外学者分别从城市交通拥挤、智能交通、物流运输等角度对如何规划城市间最优路径进行了研究。文献[2]通过对传统Dijkstra算法的研究与分析，在此基础上加入交通因素，提出一种基于城市路网的最优路径规划算法。文献[3]提出了一种基于出行者特性的最优路径搜索算法思想，在MapX矢量地图环境下对该算法进行了实现。文献[4]将人工智能领域的A*算法引入到矢量地图的最优路径搜索中来，论述了应用于矢量地图最优路径搜索的A*算法是一种完备的算法。文献[5]通过对公共交通路线票价和运作模式结构的分析，提出了一种增强的路由计算算法，给出了更合乎逻辑的不同结构结果。以上这些文献的主要研究是城市交通问题，没有涉及到城市安全问题，并且方法的时间和空间复杂度相对较高。

2 本文方法

本文提出了一种利用城市监控卡口网络寻找最优路径追踪犯罪嫌疑人的视频侦查方法，主要创新点包括：通过对城市道路监控卡口位置以及各卡口相对关系等参数进行初始化，生成城市监控卡口网络模型图G（V，E，C）；利用监控卡口采集车辆经过相邻卡口的通行时间，利用数据一致性检验、数据融合处理、自适应加权融合处理得到通行时间数据，将其作为城市监控卡口网络图中该段道路的通行能力的优化指标，对监控卡口覆盖区域内的不同道路车辆通行时间进行优化处理。将各道路最优通行时间融入到城市监控卡口网络模型图中，并运用Floyd算法规划出追踪犯罪嫌疑人的最优路径。

具体的方法流程如图1所示：

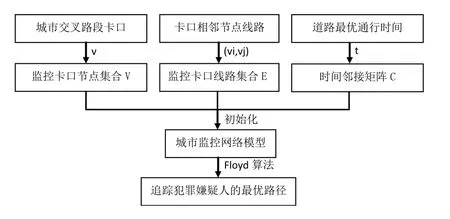
图1 基于城市监控卡口网络的最优路径规划流程图

2.1 城市监控卡口网络模型

2.1.1 城市监控卡口网络图G（V，E，C）

城市监控卡口网络图G由3部分构成：监控卡口节点集合V，监控卡口线路集合E及时间邻接矩市交叉路段卡口编号。监控卡口线路E由V中节点为0，不相邻卡口为∞。

2.1.2 Floyd算法

Floyd算法1962年由弗洛依德提出[6]，其基本思想是在有权无向图中，从j任 意j2个顶点 到 的距离的带权邻接矩阵开始，每次插入一个顶点vk，然后将 到 间的已知最短路径与插入顶点vk作为中间顶点时可能产生的路径距离比较，取较小值以得到新的距离矩阵。如图2所示为无向图是V中元素构成的无序二元组的集合，称为边集。

图2 无向图

权值也是影响最优路径选择的重要因素。Floyd算法中相邻两顶点(vi,vj)中边的权值不仅可以代表距离，在某些条件下还可以转化为成本、流量等因素，应按照实际抓捕工作的限定条件和任务需求进行设定。本文将时间作为权值，研究视频侦查工作中抓捕时间最短的最优路径问题。

2.2 道路通行能力估计方法

考虑到车辆经过道路通行时间受道路通行效率的制约，结合城市监控卡口网络提出了一种利用城市监控卡口估计车辆通行时间的方法，为城市拥堵区域追捕犯罪嫌疑目标提供辅助决策支持。在利用监控卡口估计车辆通行时间时，由于驾驶人员驾驶技能高低、现场突发状况等因素的影响，不可避免地要产生误差，影响测量数据的精确性，所以要在数据融合之前进行数据检验。

2.2.1 时间数据检验

设监控卡口在某单位时间(h)独立地进行时间数据的测量，取n个时间数据进行检验并将数据从小到大的顺序排列：T，T2…Tn。称测量时间序列下限为T，上限为Tn。

3 仿真实验

实验对象为某城市区间监控卡口网络，对监控卡口参数初始化，其中节点序列通行最优时间为xy:t（其中x、y表示相邻节点，t表示时间）。具体信息如表3所示。

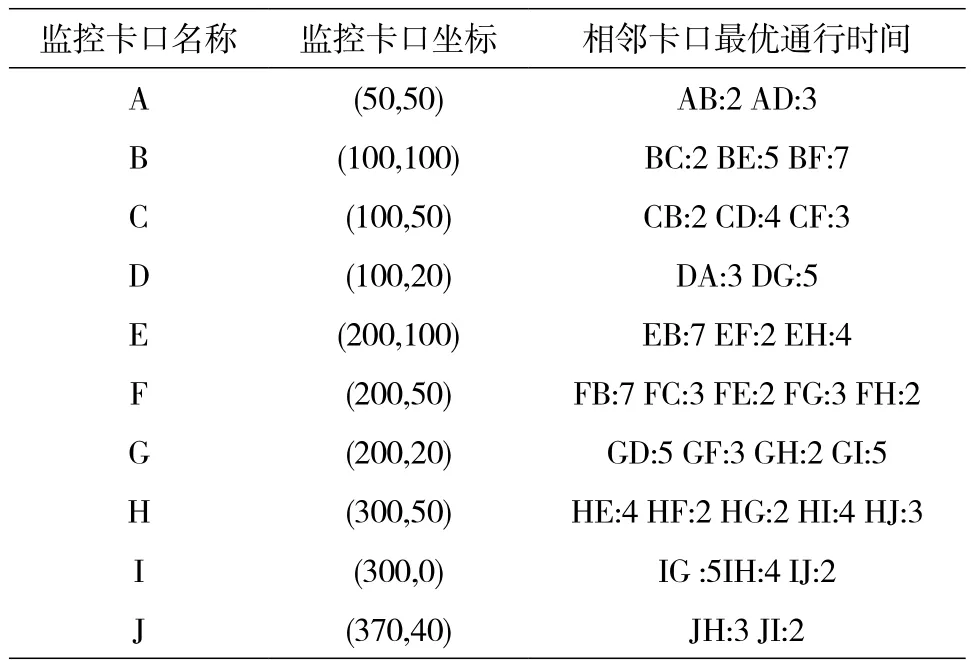
表3 道路监控卡口位置及各卡口相对关系参数

其中相邻卡口最优通行时间是由加权融合处理得到的，所构成的时间邻接矩阵C如下所示：

矩阵C中的元素dij（=2，3，…7）为顶点vi到顶点vj的时间权值即道路最优通行时间。其中dij=0为同一顶点，dij=∞为两顶点间vj不相邻。结合以上数据得到的某城市区间监控卡口网络模型图G（V，E，C），如图3所示。

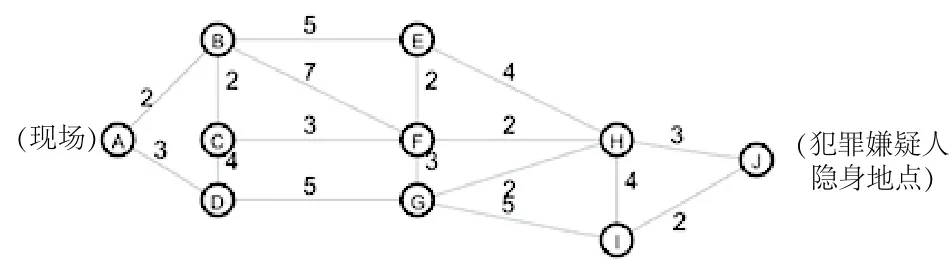
图3 监控卡口网络模型图

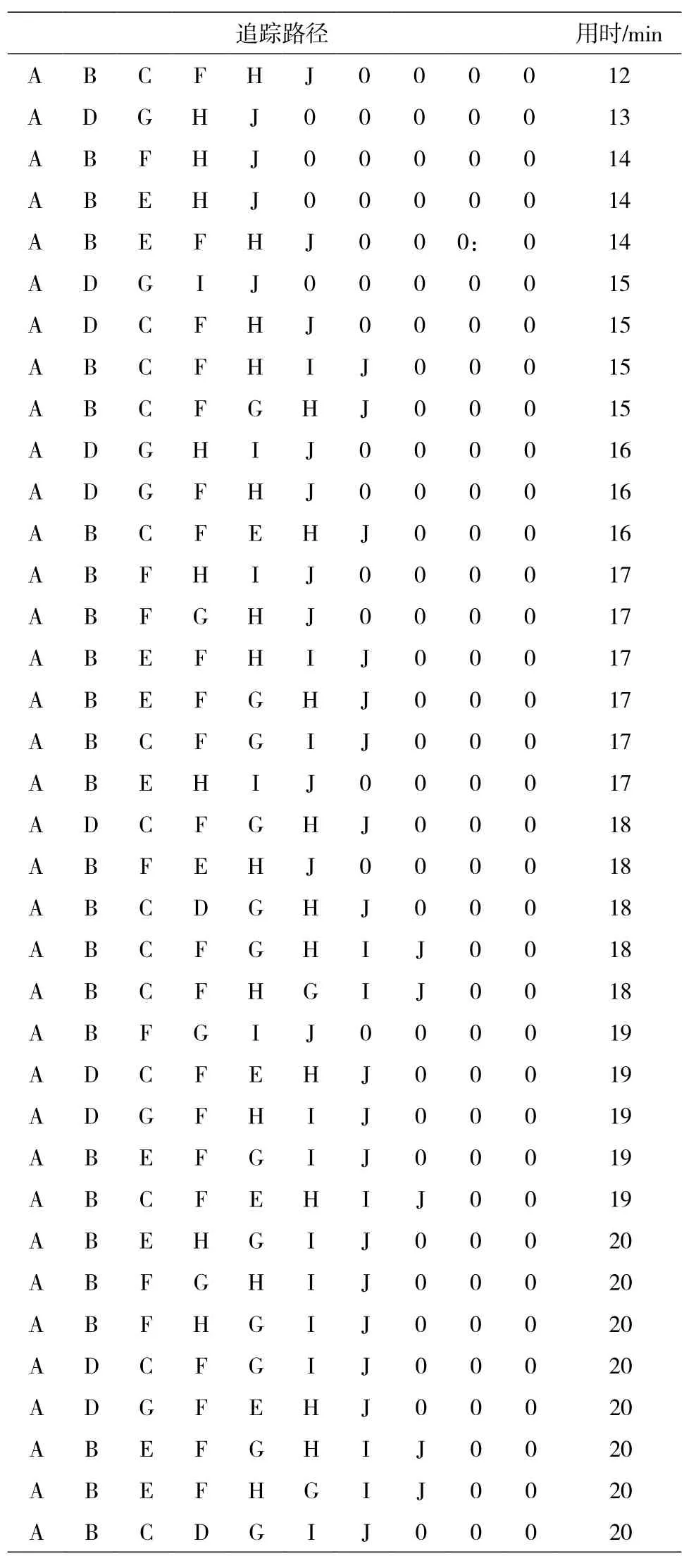
同时，按照深度优先搜索原理，得到现场至犯罪嫌疑人隐身地点所有追踪路径时间及频数，并根据用时长短和频数的多少进行分组，如表4所示。

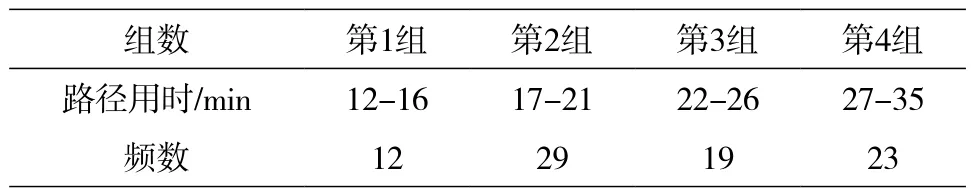
表4 路径用时频数表

取第1组追踪路径绘制折线图，如图4所示。由于监控卡口位置设定具有连续性而追踪路径卡口选择具有随机性，所以折线图会出现水平线段和线段左高右低的现象。例如，最优路径1：A B C F H J，该路径不经过D、E、G监控卡口，因此DEF段路径、FG段路径为水平线段；路径11：A D G F H J，由于卡口F顺序在卡口G之后，所以路径有左高右低现象。

图4 第1组路径图

由表4和图4可以看出，根据该城市区间监控卡口网络规划出的追踪路径共有83条（不考虑路径顺逆方向），路径较多、复杂度相对较高；其中追踪时间小于16min的路径共12条，公安人员很难准确的规划出耗时最短的追踪路径。为了验证本文方法的有效性，采用Matlab2016b进行仿真实验，针对如图3所示的监控卡口网络图规划出的最优路径如图5所示。仿真实验表明，本文提出的方法可以快速、高效的规划出现场与犯罪嫌疑人隐身地点的最优路径。最优追踪路径为：A B C F H J，用时为12min，相比其他路径该路径追踪用时最短；在Matlab2016b中运行本文算法规划最优路径用时仅为8.417676秒。

图5 基于监控卡口网络模型的最优路径

4 结束语

本文提出了一种利用城市监控卡口网络寻找最优路径追踪犯罪嫌疑人的视频侦查方法，并给出了详细的技术原理与实现步骤。仿真实验表明，本文提出的方法有效的将城市监控卡口网络和视频侦查技术结合起来，能够快速的规划出追踪犯罪嫌疑人的最优路径，丰富了现有视频侦查的技术手段，提高了视频侦查工作效率。

追踪路径 用时/min A B C F H J 0 0 0 0 12 A D G H J 0 0 0 0 0 13 A B F H J 0 0 0 0 0 14 A B E H J 0 0 0 0 0 14 A B E F H J 0 0 0： 0 14 A D G I J 0 0 0 0 0 15 A D C F H J 0 0 0 0 15 A B C F H I J 0 0 0 15 A B C F G H J 0 0 0 15 A D G H I J 0 0 0 0 16 A D G F H J 0 0 0 0 16 A B C F E H J 0 0 0 16 A B F H I J 0 0 0 0 17 A B F G H J 0 0 0 0 17 A B E F H I J 0 0 0 17 A B E F G H J 0 0 0 17 A B C F G I J 0 0 0 17 A B E H I J 0 0 0 0 17 A D C F G H J 0 0 0 18 A B F E H J 0 0 0 0 18 A B C D G H J 0 0 0 18 A B C F G H I J 0 0 18 A B C F H G I J 0 0 18 A B F G I J 0 0 0 0 19 A D C F E H J 0 0 0 19 A D G F H I J 0 0 0 19 A B E F G I J 0 0 0 19 A B C F E H I J 0 0 19 A B E H G I J 0 0 0 20 A B F G H I J 0 0 0 20 A B F H G I J 0 0 0 20 A D C F G I J 0 0 0 20 A D G F E H J 0 0 0 20 A B E F G H I J 0 0 20 A B E F H G I J 0 0 20 A B C D G I J 0 0 0 20

追踪路径 用时/min A B F E H I J 0 0 0 21 A D C F G H I J 0 0 21 A D C F H G I J 0 0 21 A B C D G H I J 0 0 21 A B C D G F H J 0 0 21 A D C B E F H J 0 0 22 A D C B F H J 0 0 0 22 A D C F E H I J 0 0 22 A D C B E H J 0 0 0 22 A B C F E H G I J 0 22 A B E H F G I J 0 0 23 A D G F E H I J 0 0 23 A B F E H G I J 0 0 24 A B C D G F H I J 0 24 A D C F E H G I J 0 25 A D C B F G H J 0 0 25 A D C B F H I J 0 0 25 A D C B E H I J 0 0 25 A D C B E F G H J 0 25 A D C B E F H I J 0 25 A B C D G F E H J 0 25 A D C B F E H J 0 0 26 A B F C D G H J 0 0 26 A B E F C D G H J 0 26 A D C B F G I J 0 0 27 A D C B E F G I J 0 27 A D C B F G H I J 0 28 A D C B F H G I J 0 28 A D C B E H G I J 0 28 A B F C D G I J 0 0 28 A D C B E F G H I J 28 A D C B E F H G I J 28 A B C D G F E H I J 28 A B E F C D G I J 0 28 A D G F C B E H J 0 29 A D C F B E H J 0 0 29 A D C B F E H I J 0 29 A B F C D G H I J 0 29 A B E F C D G H I J 29 A D G F B E H J 0 0 30 A D C B E H F G I J 31 A B E H F C D G I J 32 A D C B F E H G I J 32 A D C F B E H I J 0 32 A D G F C B E H I J 32 A D G F B E H I J 0 33 A D C F B E H G I J 35

[1]王安,魏建.城市化质量与刑事犯罪[J].山东大学学报(哲学社会科学版),2013(3):78-89.

[2]邱洋洋.基于城市路网的最优路径规划算法研究[D].北京:燕山大学,2015:5-6.

[3]杨春晓.基于MapX的最优路径搜索理论与实施技术研究[D].长春:吉林大学,2004:7-8.

[4]刘浩,鲍远律.A*算法在矢量地图最优路径搜索中的应用[J].计算机仿真,2008(4):253-257.

[5]Pun-Cheng L S C, Chan A W F. Optimal route computation for circular public transport routes with differential fare structure [J].Travel Behaviour & Society,2016(4):71-77.

[6]曾方俊.Floyd算法求解最短路径的简明方法[J].价值工程,2012(19):167-168.

[7]曹洁,徐微.基于加权平均方法的交通流检测技术的研究[C]//中国通信学会青年工作委员会.2007通信理论与技术新发展——第十二届全国青年通信学术会议论文集(下册).北京:电子工业出版社,2007:1059-1063.

[8]唐亚鹏.基于自适应加权数据融合算法的数据处理[J].计算机技术与发展,2015(4):53-56.