基于高斯混合模型的辐射源模式识别算法

，

(1. 北京理工大学机电学院，北京 100081；2. 北京遥感设备研究所，北京 100854)

0 引言

辐射源的模式识别是指在接收的辐射源信号中提取其特征信息，进行归纳、学习与记忆，当该辐射源信号再次出现时能够迅速反应。模式识别可细分为模式分类与模式学习两项中心任务。前者是判断样本在模式空间中的归属，后者对前者分类器的判决参数进行训练，形成分类判决的条件。具有自主学习能力是认知电子侦察系统的重要特征[1]，因此，作为其学习引擎核心的模式识别算法应具有在线自主学习的能力，以适应战场中随时可能出现的新的电磁威胁信号。

目前对认知电子战尚处于初级阶段，相关文献多是对概念和整体架构的介绍，较少涉及内部算法的研究。而以往关于电子侦察系统文献中对辐射源模式识别的研究工作主要集中在信号模式分类上，方法包括决策树[2]、神经网络[3-4]、支持向量机[5-6]等。然而这些算法的缺点在于其学习能力普遍较差。基于决策树的分类器一般需要预先设计好判决模型，无法在线自主改变；而神经网络与支持向量一般需要较长时间的训练才能够达到理想效果。另外，上述算法一般只能对信号分类做出非此即彼的硬判决，而不是给出信号归属的概率。针对这些问题，本文提出了基于高斯混合模型辐射源模式识别算法，该算法能够就信号在特征空间中的分布规律进行在线学习，并在模式分类中给出样本归属的概率，而不是非此即彼硬判决。另外，为了进一步提高算法学习的效率，提出基于空间网格划分的快速EM算法，以更好地适应电子战系统对实时性的要求。

1 认知电子侦察系统的工作环境

认知电子侦察设备承担认知电子战系统信息感知的任务，截获并搜集敌方辐射源的信号，从而识别敌方部队、武器或电子能力的类型和位置分布，实现战场电子对抗态势感知，从而指导进一步的行动，对关键信息链路实施电子干扰或对其物理平台进行硬性打击。

现代电子战场的环境日趋复杂，信号密度呈几何级数增加，侦察接收机的带宽内通常不再是单纯的目标信号，还存在各种各样的干扰。这里所说的干扰不仅指有意破坏性对方信息链路的压制或欺骗干扰，也包括战场上同时工作的其他雷达或电台的信号(包括己方与敌方)，这些信号与目标信号在时域、频域、空域相互交织，能够被电子战侦收设备同时捕捉到。在以往的系统中，往往需要精确已知其频点、调制、到达角等先验知识，进行多维度信息匹配来识别目标信号。然而在某些场合中，我们无法通过事先侦察等手段预知敌方信号的工作参数，这就需要在现场对信号样本进行收集，学习归纳其模式，形成动态知识库，从而实现对相似信号样本的快速识别。

以信号波形分类问题为例，假设空间中包括2FSK、4FSK、BPSK、QPSK四种调制的通信信号，它们在特征空间中的分布如图1所示(这里选取文献[2]中的三个特征值Gama_max、Sigma_AF和Sigma_AP，形成3维特征空间3，信噪比为5 dB)。已知4FSK和QPSK样本在空间中的分布模式，要解决的问题是，如何对2FSK和BPSK的分布进行建模，将其加入分类器的模式库中，并对未来的样本给出归属于库中某种模式的概率。

需要说明，本文的辐射源模式识别算法不仅是针对信号调制类型的识别，更是一种在时间、频率、调制、空间位置等多维度广义特征空间中的通用辐射源分类识别算法。对信号特征空间的选择和提取不在本文的研究范围内，主要的研究内容是在特征空间确定后如何对其中的未知模式进行在线学习与分类。下面对算法进行详细介绍。

2 辐射源模式识别算法

2.1 基于高斯混合模型的模式分类

由于辐射源信号种类的多样性，以及信号传播环境的复杂性，信号样本在特征空间中可能会呈现出不规则的分布。而高斯混合模型就提供了这样一种可对任意复杂模式进行拟合的手段。

通过信号样本在D维特征空间D中的大量累积(对于高采样率的电子侦察系统很容易达到)，可以获得每一种信号模式在特征空间中的分布密度，该分布密度反映了模式h分布概率的空间密度函数ph(x)，其中x是属于D的D维特征向量。高斯混合模型GMM具有对各种形式的概率密度函数进行统一拟合的能力[7]。GMM定义为K个高斯分布的加权和，每个高斯分布称为一个分量，表示为：

(1)

因为每个GMM分量可以捕捉局部的数据特征，而混合模型有能将所有这些局部特征进行综合，形成全面且具体的分布函数。这样避免了为每一种特征值的组合定义专门的密度函数，增加了模式分类器的通用性、灵活性与可扩展性。

2.2 基于EM算法的GMM拟合方法

GMM的拟合可以用EM算法实现。EM算法可以从不完全数据集中获得对参数的极大似然估计，是一种有效而又实用的机器学习算法。这里所谓的“不完全数据”是指对参数直接进行似然估计比较困难，而在引入辅助性的参数(这些参数通常表征样本背后隐含的信息)后就会比较顺利，于是将原始观察数据加上辅助性数据称为“完全的数据”。

EM算法的每一步迭代包括：1)E步骤——期望步骤(Expectation Step)；2)M步骤——极大似然步骤(Maximum Likelihood Step)。EM算法利用极大似然的原则，首先对模型参数给出一个初始猜测，然后开始进行迭代，以获得更佳的估计模型参数，可证明它在一定意义下可靠地收敛到局部极大，当似然函数值是有界的时候，迭代序列收敛到一个稳定值的上确界[8]。

EM算法的基本原理如下：假设观察到的数据是X，完全数据Y=(X,Z)，Z是缺失数据。θ是GMM模型参数，在Z缺失的情况下，X关于θ的似然函数p(X|θ)很复杂，难以对θ进行极大似然估计。先对确实数据Z进行假设，这样就可能得到一个关于θ的似然函数p(X,Z|θ)，以便对模型参数θ进行优化。回过头来，利用优化后的模型又可以对Z的上一次假定进行评价和改进。如此迭代，将获得对Z及θ的局部最优估计。具体步骤如下[8]：

设置辅助函数(2)，该函数表示在已知上一步模型参数θt-1的情况下，完全数据对数似然函数的数学期望。

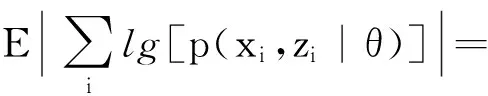
(2)

令rik≜p(zi=k|xi,θt-1)，代表第k个分量在数据元素xi中占据的份额。则：

(3)

在E步骤中，估计rik的值：

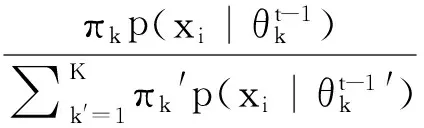
(4)

在M步骤中，估计每一个分量的权重πk为：

(5)

rik是第k个分量在元素xi中占据的份额，rk代表第k个分量在所有样本数据中所占的总份额，N为样本总数。

对于高斯分布来说，θk包括均值向量μk以及协方差矩阵Σk。

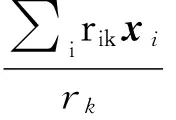
(6)

(7)

在完成对πk以及θk的估计之后，将其代入步骤进行新一轮迭代，从而获得GMM表达式(1)中未知参数的稳定估计。

2.3 基于网格空间的快速EM算法

可以看出，EM算法的每一次迭代都需要遍历所有的数据元素，对于大样本来说，计算量非常庞大。当需要对GMM模型进行在线拟合，系统的实时性会受到很大影响。因此本文设计一种基于网格空间的快速EM算法。其主要思想是将空间进行网格量化，并将网格的权重纳入EM估计的计算中。

如图3所示，特征空间被划分为L个单元格，设第j个单元格中存在Mj个数据元素，每一个单元格中元素的特征向量用xij表示，其中i=(1,2,…,Mj)，j=(1,2,…,L)。

EM算法中的E步骤为：

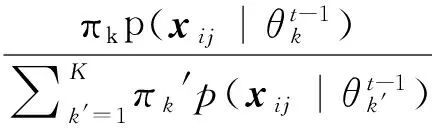
(8)

对同一单元格，rijk是一样的，将其统一表示为rjk。这样只需要对每个单元格计算一次即可。则：

(9)

由于经过了网格量化，特征向量xij近似用网格中心点的向量xj表示。每个单元格的均值向量μk以及协方差矩阵Σk的计算为：

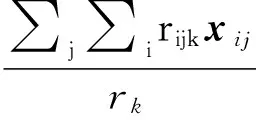
(10)

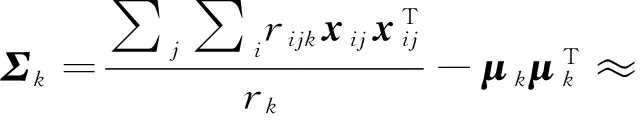
(11)

其中，Mj代表了不同单元格因内部元素数目不同在整体参数估计中的权重。可见，通过网格化处理，EM算法的计算复杂度从O(NK)降低到O(LK)，其中N为样本点数，L为网格单元数，K为所需的GMM分量个数。可见计算量被极大缩减，而且不管样本点数N有多少，只要采用同一种空间网格划分方式，L即为固定数值。从而使计算量摆脱样本点数的限制。

下面对上述方法的计算量和拟合精度进行仿真分析。30 000个样本在特征平面上的分布如图4(a)所示，用64×64的网格量化，GMM模型采用4个分量拟合。网格化EM算法得到的拟合结果如图4(b)所示，得到的拟合参数如表1所示。同时，对同一组数据用逐点计算的方法进行GMM拟合，得到的四个GMM分量的参数如表2所示。与表1中的数值对比，二者的吻合程度较高。在计算时间上，采用相同的电脑和Matlab版本，逐点EM算法的计算时间是14 361 ms，而网格EM算法的计算时间是2 930 ms。

采用网格化的处理方法非常适用于电子侦察系统，其理由包括如下两点：

1) 在现实系统中，受限于噪声及量化误差等因素的制约，参数的测量精度会存在上限，此时对数据采用更高的表达精度是没有意义的，为了不浪费系统的处理器资源，只需要将网格分辨率与该、上限匹配即可。

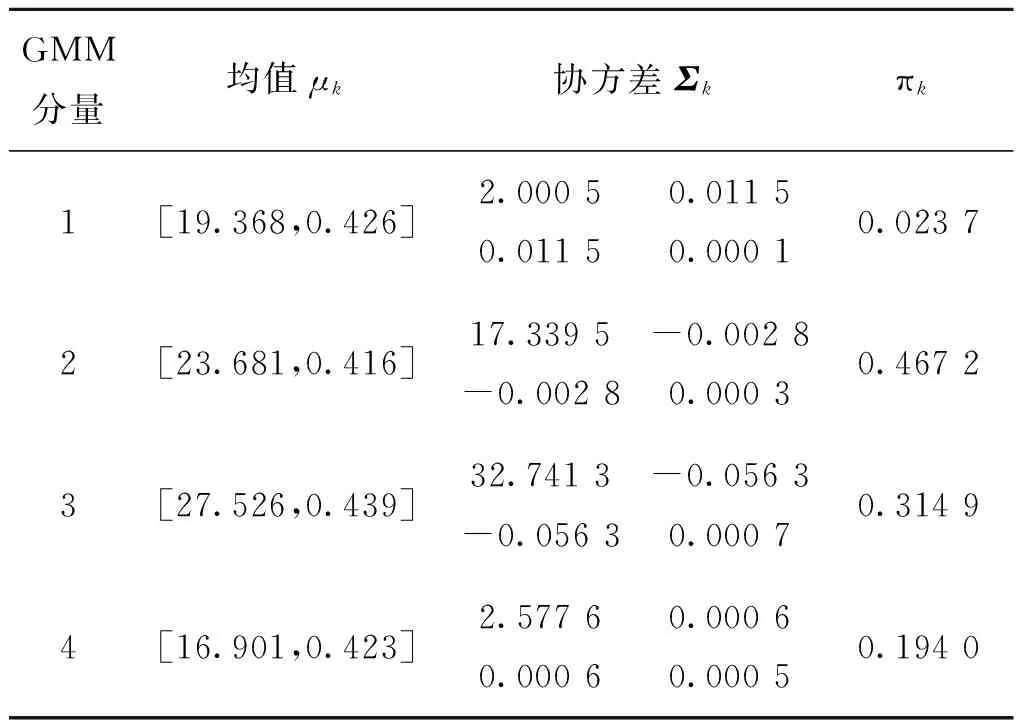
GMM分量均值μk协方差Σkπk1[19.368,0.426]2.00050.01150.01150.00010.02372[23.681,0.416]17.3395-0.0028-0.00280.00030.46723[27.526,0.439]32.7413-0.0563-0.05630.00070.31494[16.901,0.423]2.57760.00060.00060.00050.1940

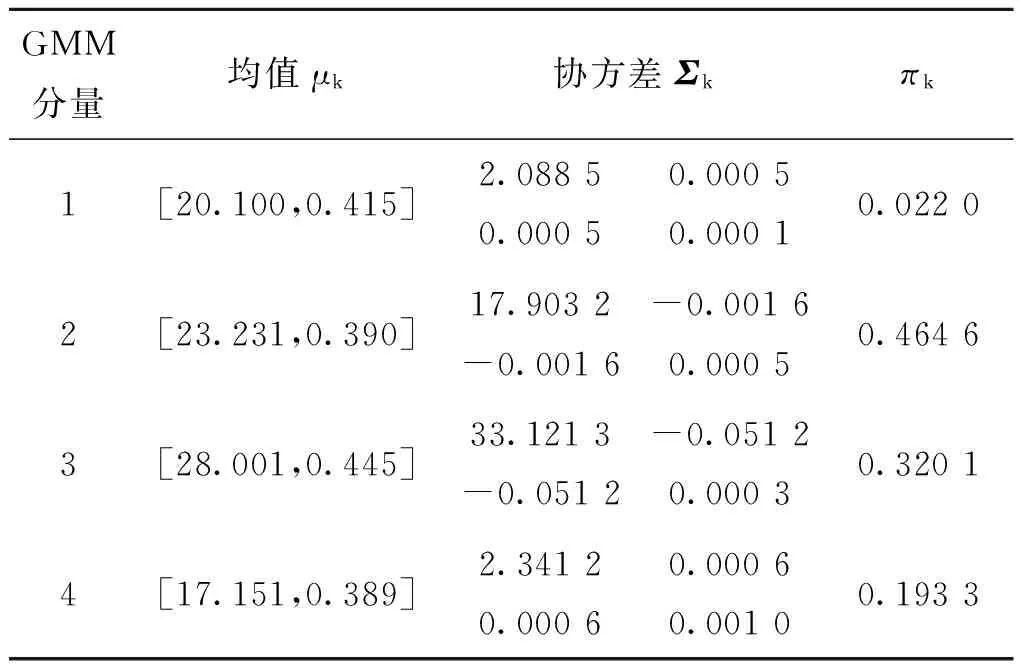
表2 逐点拟合的GMM分量参数Tab.2 The GMM component parameters of dotk-by-dot EM method

2) GMM的拟合准确度与样本积累的数量有很大关系，数量越大，其分布概率越明显、越稳定。采用网格化的方法摆脱了样本点数与计算量的关系，可以积累更多的点获得更精确的分布概率，这一点对于实时系统具有十分重要的意义。

2.4 辐射源模式识别的整体流程

辐射源模式识别算法完成对接收信号的分类与学习。对于信号样本，首先判断其是否与已知的辐射源模式吻合。根据存储的GMM模型得到样本在各种模式中的似然概率，设样本为x，则样本归属模式h的似然概率为：

(12)

其中，模式h的GMM由序号K1至Kh的分量拟合而成。

遍历所有模式，若最大似然概率超过门限，则给出样本的归属，否则启动模式学习进程。在模式学习中，需要经过一段时间的样本积累获得稳定的统计特性，然后通过聚类分析(为了与本文的网格化拟合算法统一，采用了一种基于分水岭变换的网格聚类方法[9])在特征空间中分离出待学习的新样本集，利用基于网格空间的快速EM算法在线拟合其GMM模型，加入分类器的动态知识库，即可完成对未定义信号模式的学习。整体流程图如5所示。

3 仿真及分析

3.1 对辐射源空间分布模式的学习与分类

第1步，对新出现辐射源的学习:

仿真条件如下：接收机带宽为20 MHz，信噪比为5 dB，采用和差比幅测角体制。初始状态下，方位角、俯仰角二维空间中分布着两个辐射源，其样本集即图6(a)编号为1、2的点簇，这两个辐射源已保存在GMM模型库中。新出现的辐射源为编号为3的点簇，其中包含500个样本。

算法能够识别出新出现的辐射源，并启动学习进程，对其进行聚类与GMM拟合学习，最终系统中的GMM模型库如图6(b)所示。

第2步，对样本分类：

采用相同的仿真设置，随机产生样本，归属于上述三个辐射源其中之一，经过1 000次蒙特卡洛试验，样本分类准确率为99.53%。样本分类结果如图7所示。

3.2 对信号调制模式的学习与分类

假定的应用场景是雷达脉冲信号的分类，信号类型包括常规脉冲、线性调频、BPSK巴克码、Costas离散频率编码四种。信号参数如表3所示。

信号特征选用文献[10]中的4种特征，分别是:

1)归一化复包络能量谱密度最大值ρmax。

2)归一化复包络平方的能量谱密度最大值ρ2,max。

4)信号时频分布的离散能量聚集区的数量Nobj。

表3 测试样本信号参数Tab.3 The parameters of testing signals

采用这些特征可以保证上述4种信号在特征空间中有较好的区分度和内聚性。

信号脉冲各20 000个，前一半用于分类器的自主学习，后一半用于检验分类器的效果。各信号类型随机出现，出现的总次数基本一致。各个信号的参数如表4所示。噪声为加性高斯白噪声，在各信噪比下，由自主训练的分类器对信号的正确分类概率如表4所示，在SNR为10 dB的情况下，正确率达到了98%以上。

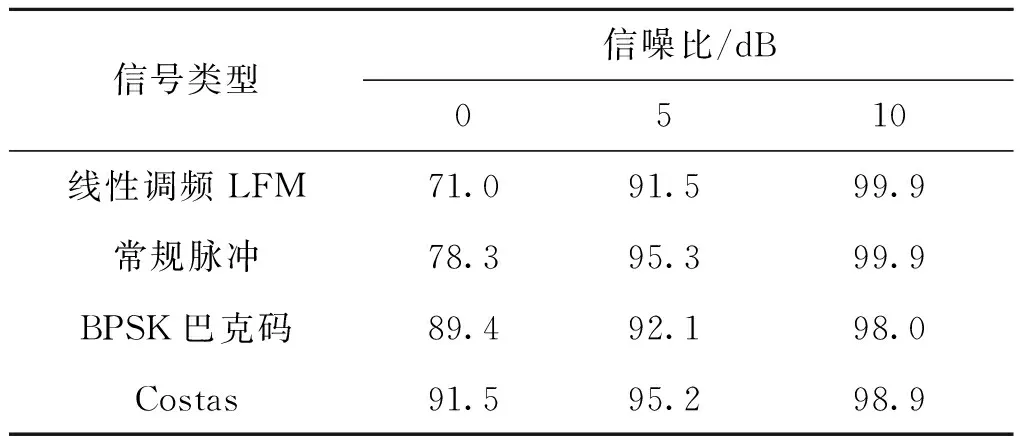
表4 信号的正确识别概率(%)Tab.4 The accuracy of signal recognition

4 结论

本文提出了基于高斯混合模型的辐射源模式识别算法。该算法能够对各类辐射源进行在线学习，对各种模式的适应性较强，能够形成模式的似然概率模型。仿真分析表明：算法能够对各类辐射源进行在线学习与分类，适应性较强，且计算效率较传统EM算法有较大提高。本算法的主要缺点在于当特征空间维数升高时，计算量将呈几何级数递增。因此在未来的工作中，可就具体的应用场景尝试特征值的精简、空间降维、子空间联合判断等途径研究进一步提高算法计算速度的方法。

[1]张春磊, 杨小牛. 认知电子战初探[J]. 通信对抗, 2013(2):1-4.

[2] Nandi A K, Azzouz E. Algorithms for automatic modulation recognition of communication signals[J]. Communications IEEE Transactions on, 1998, 46(4):431-436.

[3]陆渊章, 陆锦军, 张冰. 基于等价型模糊神经网络的战场辐射源识别算法[J]. 现代雷达, 2015, 37(1):49-51.

[4] 顾阳阳. 基于流形学习的雷达辐射源识别技术[D]. 西安：西安电子科技大学, 2014.

[5] 张葛祥. 雷达辐射源信号智能识别方法研究[D]. 成都: 西南交通大学, 2005.

[6] 潘莹. 典型信号模式识别算法的研究与应用[D]. 北京：北京邮电大学, 2014.

[7] Yu Guoshen. Solving inverse problems with piecewise linear estimators: from gaussian mixture models to structured sparsity[J]. IEEE Transactions on Image Processing, 2012, 21(5): 2481-2499.

[8] Murphy Kevin P. Machine Learning A Probabilistic Perspective[M]. New York: the MIT press, 2012.

[9] Lolla S V G, Hoberock L. Improved unsupervised clustering over watershed-based clustering[C]// Ninth International Conference on Machine Learning and Applications. IEEE Computer Society, 2010:253-259.

[10] Jarmo Lundén, Visa Koivunen. Automatic radar waveform recognition[J]. IEEE journal of selected topics in signal processing, 2007, 1(1): 201-213.