基于最小二乘法的数据采集仪电压校准系数提取方法

， ，，

(西安机电信息技术研究所，陕西 西安 710005)

0 引言

数据采集仪在引信电池的性能测试中得到了越来越多的使用，采集电压的精准度对引信电池的工作电压、工作时间以及激活时间的测定有着重要影响。数据采集系统的校准，是一项繁琐而数据庞大的计量工作，准确高效地校准成为亟待解决的问题[1]，然而，数据采集仪数据的准确性直接影响到整个测试系统的性能[2]。文献[1]设计开发了数据采集系统校准数据处理及校准证书自动生成软件，文献[3]设计开发了数字采集仪在线自动校准系统，构建在线校准系统的总体框架，文献[4]介绍了一种专用数据采集卡自动校准系统。以上校准或提高精确性的方法都需要配备专业数据采集板卡或校准硬件，成本较高[5]。最小二乘法及其改进方法已被广泛运用于校准定位精度和故障诊断模型等领域[6-7]。传统的线性校准系数只适应开放性操作不适用于黑匣子采集模式的电压数据校准，只能使用通过原点的直线获得校准系数来消除线性误差，无法消除非线性误差。本文针对上述问题，提出了基于最小二乘法的数据采集仪电压校准系数提取方法。

1 线性校准及最小二乘法

1.1 线性校准

线性校准系数的获取流程如图1所示。含有线性校准过程的电压读取流程如图2所示。

用稳压电源作为数据采集仪的输入，调节稳压电源到两组不同的电压，记录实际输入电压值(x1,x2)，用数据采集仪进行采集，采集后读取测量电压(y1,y2)，令：

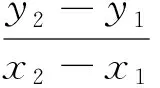
(1)

则接下来采集出来的yi有：

yi=kxi

(2)

由此可以看出，传统的线性校准系数必须准确地知道输入的电压真值，但在实际电池性能测试中，电压是一个随时间变化的变量，想要实时记录不现实。参与获取线性系数的参数点有限，具有一定的局限性，只能应用于开放性操作，对于目前流行的黑匣子电压记录模式根本不可行。另外可以看出该系数只能适用于线性误差，对于非线性误差无法消除，反而可能因为努力消除线性校准带来更大的误差。

1.2 最小二乘法

最小二乘法是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配[8]。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。在研究两个变量(x,y)之间的相互关系时，通常可以得到一系列成对的数据(x1,y1;x2,y2;…xm,ym)，将这些数据描绘在x-y直角坐标系中，若发现这些点在一条直线附近，可以令这条直线方程为：

y=ax+b

(3)

其中，a,b为任意实数。

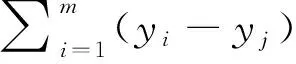
2 基于最小二乘法的数据采集仪电压校准系数

基于最小二乘法的数据采集仪电压校准系数主要分两步：一是在数据采集仪采集电池电压前在外部对数据采集仪进行校准，计算好校准参数；二是在读取软件中设定校准参数，再对黑匣子数据采集仪电压数据进行读取，该数据即是校准后的数据。使用最小二乘法对数据采集仪进行校准的流程如图3所示。

用稳压电源作为数据采集仪的输入，调节稳压电源到不同的电压，记录实际输入电压值(x1，x2，…，xm)，用数据采集仪进行采集，采集后读取测量电压(y1，y2，…，ym)，令：

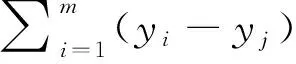
(4)

把式(1)代入式(2)中得：

(5)

当∑(yi-yj)2最小时，可用函数φ对a、b求偏导数，令这两个偏导数为零。

(6)

即

(7)

把括号内的各项进行整理合并，并把未知数a、b分离出来，便得：

(8)

得到的关于a、b为未知数的两个方程组，即校准的回归数学模型。解这个方程组得出a、b值，即得出某一数据采集仪的校准系数。即使同一批次的数据采集仪，也应该各有各的校准系数。

在回归过程中，回归的关联式不可能全部通过每个回归数据点(x1,y1;x2,y2;…；xm,ym),为了判断关联式的好坏，可借助相关系数R、统计量F、剩余标准偏差S进行判断。

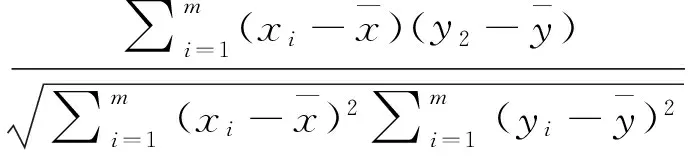
(9)

R越趋近于1越好，F的绝对值越大越好，S越趋近于0越好。

由此可见，基于最小二乘法的数据采集仪电压校准系数在进行电池电压采集前对数据采集仪进行校准，该系数考虑到了所有参数点的电压，以实测值和真值的偏差的平方和最小为依据，让数学模型尽可能多地通过参数点，消除大部分的非线性误差，该校准系数还可以自身进行好坏判定，以使模型达到最优。

3 实验验证

3.1 数据采集仪校准前后数据准确度对比

用稳压电源作为数据采集仪的输入，调整多个不同的直流电压值进行输入，用数据采集仪进行采集，采集后读取测量电压，填入表1中。

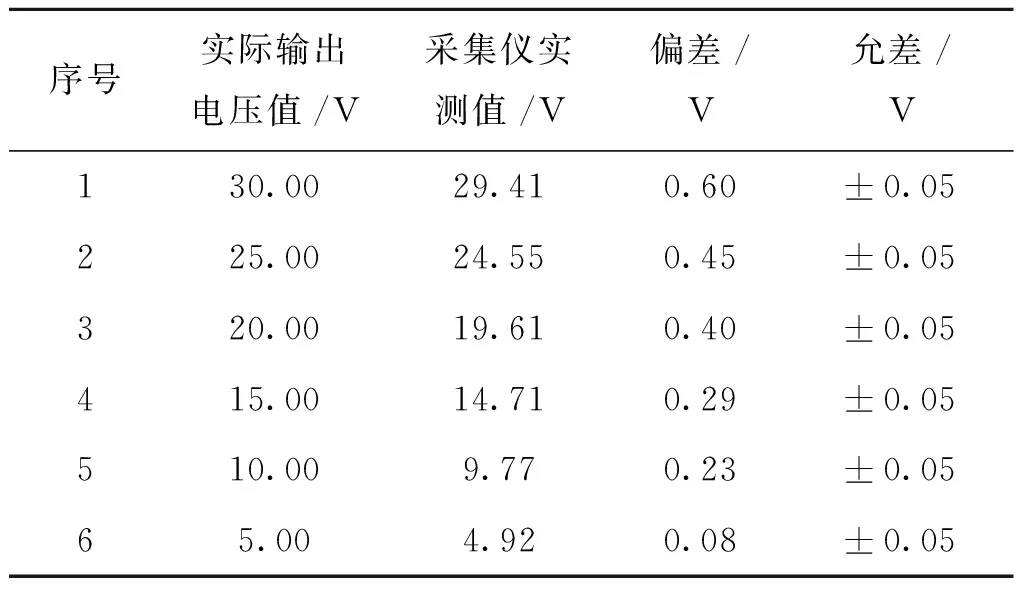
表1 校准前直流电压记录Tab.1 DC voltage records before calibration

(10)

解得a=1.019，b=0.007。

因此基于最小二乘法的校准电压曲线公式为y=1.019x+0.007。据式(9)，解

R=0.999≈1

相关系数R值几乎为1，可见校准公式与数据点相关性很好。

根据图2的流程，在数据采集仪的读数软件中将a值1.019和b值0.007输入，即完成了数据采集仪的校准，校准后再进行电压采集和读数，记录结果如表2。

为了进一步对比数据采集仪校准前后电压数据的准确度，将表1和表2中的数据进行对比，如图4所示。

校准前后数据采集仪对某一单个电池采集的电压数据激活段的对比如表3所示。

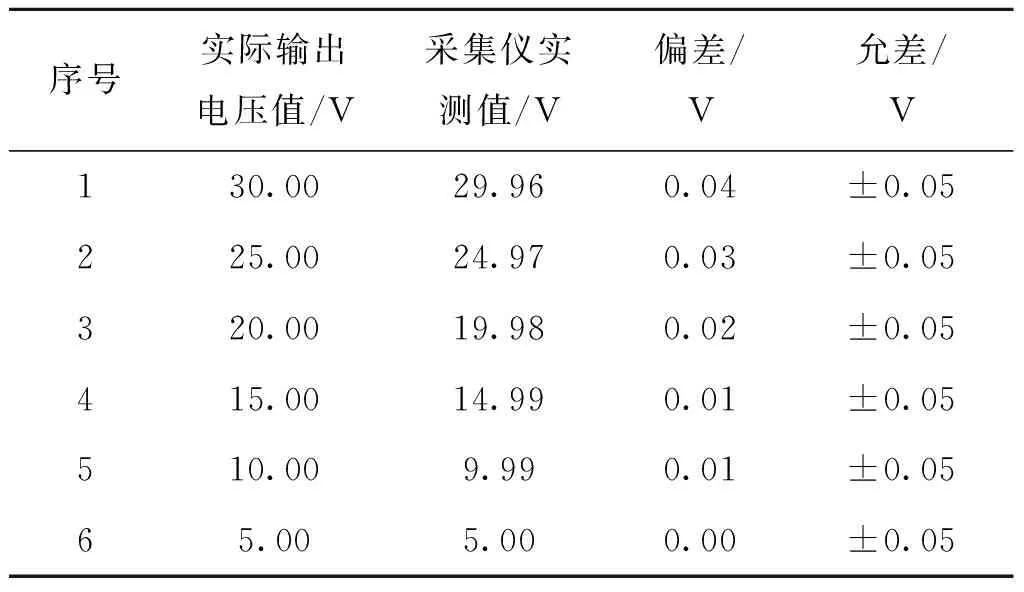
表2 校准后直流电压记录Tab.2 DC voltage records after calibration

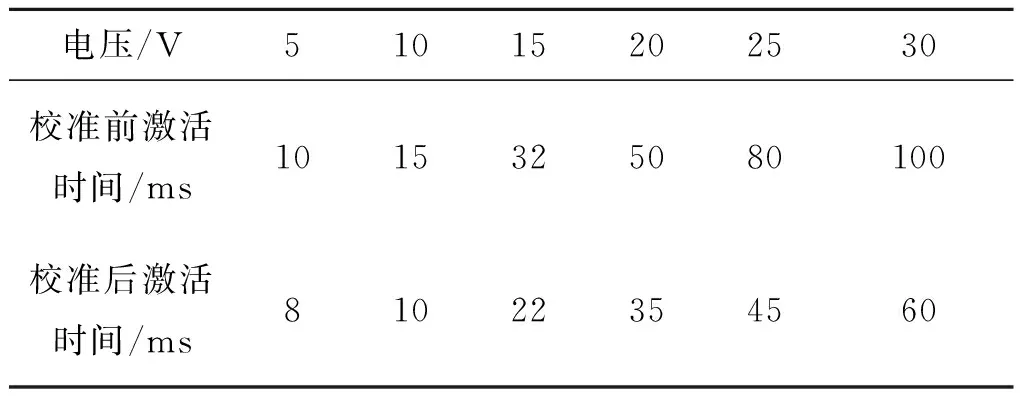
电压/V51015202530校准前激活时间/ms1015325080100校准后激活时间/ms81022354560

通过图4可以看出，校准后的电压数据相比于校准前的电压数据误差更小，准确度更高，更接近电池电压实际真值。由表3可以看出，校准后的电压激活段的数据准确性可以提高20%～40%。

3.2 Excel数据拟合验证

为了进一步验证本文校准系数的校准效果，采用Excel进行最小二乘法拟合验证，当数据量较大时也可以采用此系数以减少人工计算量。图5所示为电压数据及图表类型，图6为曲线参数选择，图7为拟合曲线，可直观看出系数及R值。

由图7中可以直观地看出，拟合曲线公式为y=1.019x+0.008，其中a，b，R的值分别为1.019，0.008，1。

对基于最小二乘法的数据采集仪电压校准系数实验验证表明：

1)基于最小二乘法的数据采集仪电压校准系数在数据采集仪采集前用外接电源进行校准，适用于目前流行的黑匣子采集模式。

2)按该系数建立的数学模型考虑了所有参数点，与参数点相关性很好，可有效消除非线性误差。

3)校准后的电压数据更接近于实际真值、激活段的数据准确率可以提高20%以上。

4 结论

本文提出了基于最小二乘法的数据采集仪电压校准系数提取方法。该系数采用最小二乘法原理对采集数据建立数学模型，将该数学模型的系数作为数据采集仪的校准参数。针对某一单个数据采集仪，将稳压电源作为输入，采集得到一组电压数值，利用数学模型对电压数值进行线性回归，得到该数据采集仪的校准系数，在读数软件中进行校准，可以降低读取电压的偏差，提高数据采集仪的测试准确率。实验表明，该系数建立的数学模型考虑了所有数据点，与参数点相关性很好，可有效消除非线性误差，校准后的电压数据更接近于实际真值，激活段的数据准确率可以提高20%以上。

[1]张宇,常艳.数据采集系统校准研究[J].电子测量技术,2012(8):23-27.

[2]谭灰庆,孟升卫,尹洪涛.VME数据采集模块设计与校准方法研究[J].电子测量技术,2011(4):38-42.

[3]杨慧玉,任兵,合烨,等.基于LabVIEW的数字采集仪在线校准系统设计与开发[J].中国测试,2013(1):33-36.

[4]刘天时,龙文,马宇.一种数据采集卡自动校准系统及关键技术研究[J].宇航计测技术,2013(2):48-52.

[5]谢锐，裴东兴，王勇贞.可编程引信高速编码信号测试仪[J].探测与控制学报，2016，38(6)：26-30.

[6]李涛，屈也频，梅风华.基于总体最小二乘的多基地声纳系统定位算法[J].探测与控制学报，2015，37(3)：82-85.

[7]宋涛，舒涛，刘进，等.基于改进最小二乘支持向量机的柱塞泵故障诊断模型[J].控制与控制学报，2015，37(4)：91-95.

[8]同济大学数学系.高等数学[M].北京:高等教育出版社,2013.