四旋翼飞行器的RBF 网络自适应滑模控制
韩业壮,华 容
(上海应用技术大学电气与电子工程学院,上海 201418)
四旋翼飞行器的RBF 网络自适应滑模控制
韩业壮,华 容
(上海应用技术大学电气与电子工程学院,上海 201418)
针对带有不确定性的四旋翼飞行器系统,提出一种滑模控制和神经网络自适应相结合的混合控制方法。该方法在滑模控制的基础上,考虑到实际系统中通常存在建模不精确、参数未知等不确定性,构造RBF神经网络在线逼近系统模型的未知函数,采用Lyapunov方法设计自适应律在线估计神经网络权值和模型未知参数,并通过Lyapunov定理验证了系统的稳定性。仿真结果表明,该方法相对于RBF神经网络的自适应PID控制,具有更短的调节时间、更小的超调量和更好的抗干扰能力,同时在模型参数发生变化的情况下,该控制器的鲁棒性能更强。
四旋翼飞行器; 滑模控制; 神经网络; 自适应律
0 引言
四旋翼飞行器是一种具有垂直起降和悬停功能的蝶形飞行器,具有结构简单、体积小、机动灵活的优点。对于四旋翼飞行器的控制,主要有以下难点:1) 建立准确的动力学模型非常困难,飞行过程中系统会受到重力、陀螺效应和外界干扰的影响;2) 四旋翼飞行器是具有6个自由度,4个输入量的欠驱动系统,具有高度的非线性、强耦合性等控制难点[1-2]。对于四旋翼飞行器控制系统的设计,目前常用的控制算法有自适应控制[3]、反步法[4]、滑模控制[5]和鲁棒控制[6]等,都取得了一定的研究成果,但如何解决控制器对模型较强的依赖,并提高闭环系统鲁棒性,是实现带有不确定性四旋翼飞行器控制的关键。针对带有不确定性的四旋翼飞行器系统,有学者提出RBF神经网络自适应PID控制算法[7],基本思想是在PID 算法的基础上利用神经网络选择和整定PID参数,神经网络的自学习自适应能力虽然具有一定的非线性控制作用,但控制器中的PID算法是传统的线性控制方法,不太适合四旋翼飞行器这种非线性系统。滑模控制能为含有不确定性的非线性系统提供有效的鲁棒控制,因此,利用RBF神经网络的自适应滑模控制方法设计了飞行器的位置和姿态控制器,并与RBF网络自适应PID控制算法进行仿真对比,证明该方法具有更好的轨迹跟踪、抗扰动和参数适应能力。
1 四旋翼飞行器动力学模型
建立合适的四旋翼飞行器的数学模型,是下文设计控制器的前提。为了便于分析,现将四旋翼飞行器的模型简化为如图1所示的结构示意图。

图1 四旋翼结构示意图Fig.1 Structure diagram of quadrotor

定义1U1,U2,U3,U4为四旋翼飞行器的4个独立控制通道的控制输入量,Ωi(i=1,2,3,4)为各个旋翼的转速。则系统的控制输入量为
(1)
式中,b,w分别为旋翼升力系数和阻力系数。
四旋翼飞行器的动力学模型为[8]
(2)
式中:Ixx,Iyy,Izz分别为飞行器在机体坐标系各个轴向的转动惯量;Ir为转子转动惯量;Ωr=-Ω1+Ω2-Ω3+Ω4,为旋翼产生的陀螺效应分量;l为飞行器质心到各旋翼中心的距离;m为飞行器质量。将式(2)写成状态方程形式,即

(3)
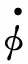
(4)

(5)
假设1所有状态变量均可以得到且用于反馈。
假设2系统物理参数Ixx,Iyy,Izz,Ir,l均未知,即b1,b2,b3为未知参数,f1(x),f2(x),f3(x),g(x)为具体形式未知的函数[9]。
假设3理想轨迹有界,其一阶二阶导数存在。
2 四旋翼飞行器控制器设计
鉴于四旋翼飞行器具有欠驱动、强耦合和非线性等控制难点,控制器采用分环控制的结构形式。其中,外环为位置控制器,内环为姿态控制器,控制系统结构如图2所示。
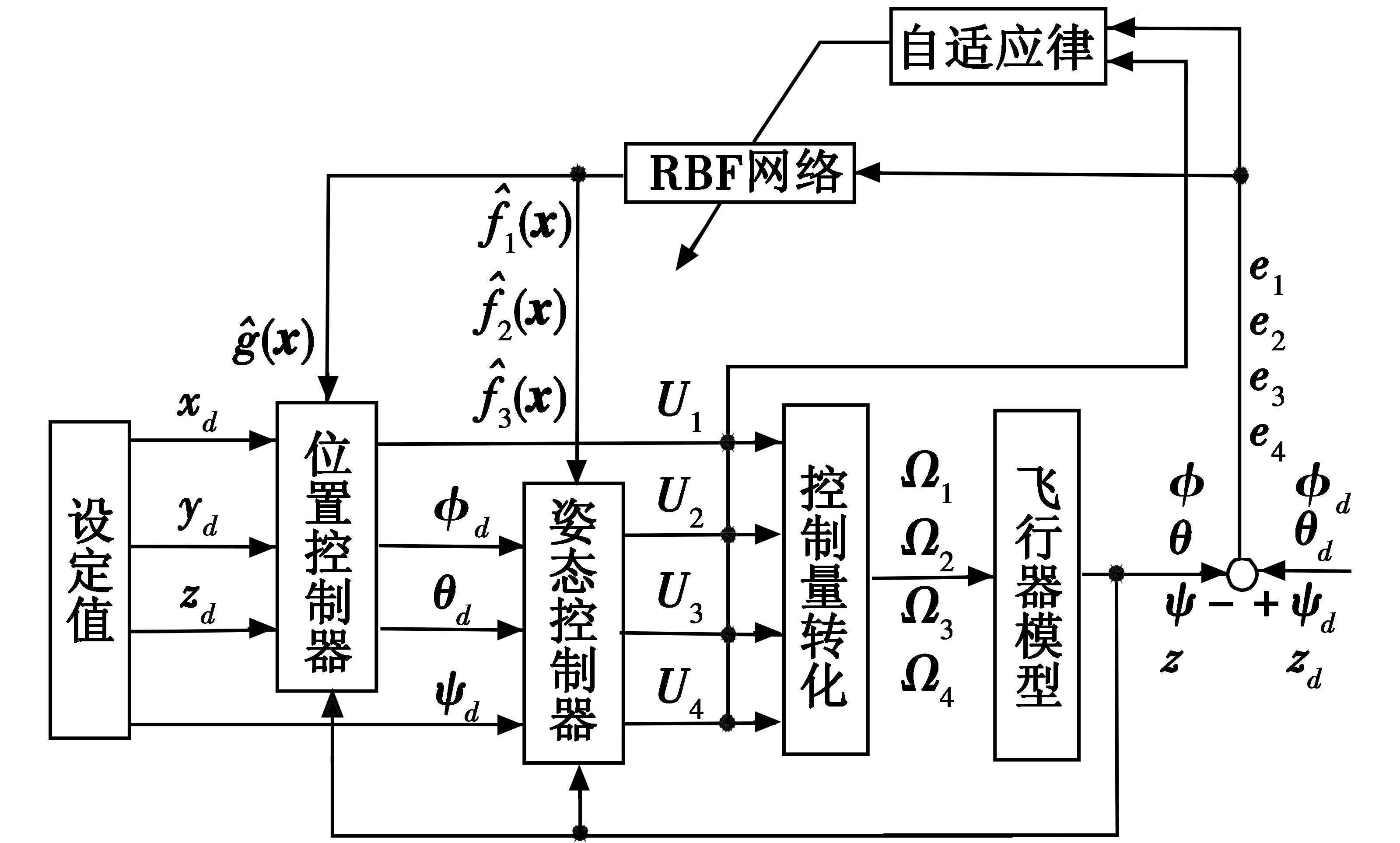
图2 控制系统结构图Fig.2 Structure diagram of controller

2.1 位置控制器设计
位置控制分为高度控制通道和水平控制通道。高度z由控制量U1决定,U1得到的升力,作为两个模块的输入,一个是作为系统总升力输入到四旋翼系统,另一个是用于水平位置控制通道的横滚和俯仰角的反解算模块。
考虑高度z的空间表达式
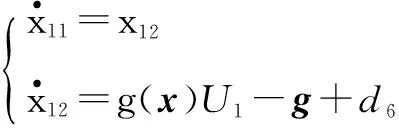
(6)
定义理想跟踪指令为zd,跟踪误差为
e1=zd-z。
(7)
设计滑模面[10]为
(8)
(9)
设计滑模控制律为
(10)

(11)
(12)




(13)
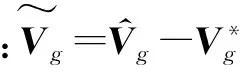
选择Lyapunov方法在线调整神经网络权值,避免了RBF网络自适应PID控制算法中采用的梯度下降法求权值易陷入局部最优,不能保证闭环系统全局稳定性的局限性,定义Lyapunov函数为
(14)

(15)
由Lyapunov稳定性设计自适应律为
(16)

(17)

水平方向x,y的子系统是欠驱动系统,与φ,θ动态耦合,即由控制量Ux,Uy控制。
用同样的推导方法得到虚拟控制量
(18)

(19)
根据式(5)变量之间的非线性约束关系,可以得到姿态子系统的中间指令信号为
(20)
将ux,uy代入式(20)可得φd,θd。
2.2 姿态控制器设计
姿态角系统相对于位置子系统是独立的。以横滚角φ为例,设计姿态角的RBF网络自适应滑模控制律,考虑横滚角φ的空间表达式
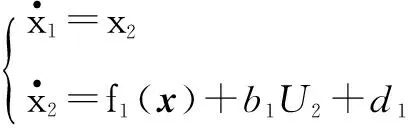
(21)
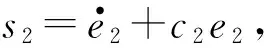
由高度z推导过程可知横滚角的滑模控制律为
(22)
(23)
(24)
式中,εf1为网络的逼近误差,εf1≤εmaxf。

(25)

定义Lyapunov函数为
(26)
式中:γf1>0;γb1>0。
对式(26)求导并将式(25)代入可得

(27)
取自适应律为
(28)
(29)
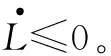
可见,控制律中的鲁棒项η2sgns2的作用是克服干扰和神经网络逼近误差,以保证系统稳定。
用同样的推导方法可以得到控制律U3,U4,即
(30)

(31)
相应的自适应律为

(32)

(33)
式中:v(t)为待微分的输入信号;ε=0.04;x1为对信号进行跟踪;x2为信号一阶导数的估计;x3为信号二阶导数的估计。
为了防止抖振,采用“边界层”方法,控制律中采用饱和函数sat(s)代替符号函数sgns,即
(34)
式中:δ>0,为边界层厚度。
3 仿真分析
3.1 仿真参数
用Matlab对RBF神经网络自适应滑模控制算法(ASMCNN)进行仿真,并与RBF神经网络自适应PID控制算法(APIDNN)对比,验证控制器的轨迹跟踪、抗扰动以及鲁棒性能。系统物理参数选取为:m=0.53 kg,Ixx=Iyy=0.006 2 kg·m2,Izz=0.011 2 kg·m2,Ir=6E-5 kg·m2,l=0.232 m,g=9.8 m/s2,升力系数b=3.13E-5 N·s2,阻力系数w=7.5E-7 N·ms2,假设系统外界扰动上界D=0.2。
设置初始位置为(000)T,初始姿态为(000)T。期望航迹xd=cost,yd=sint,zd=t,期望偏航角ψd=1。
3.2 跟踪性能对比
飞行器飞行过程中,需要实时改变飞行位置,所以跟踪性能的优劣决定着控制器的控制品质。飞行器轨迹跟踪曲线如图3、图4所示。
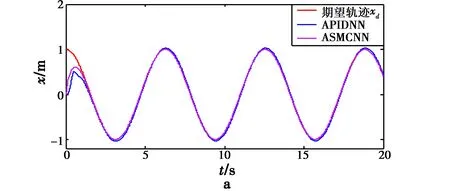


图3 飞行器位置跟踪曲线Fig.3 Position tracking of quadrotor
由图3和图4可以看出,两种控制器都完成了轨迹跟踪任务,但RBF网络自适应滑模控制算法比RBF网络自适应PID算法调整时间更短,且没有超调量,而RBF网络自适应PID算法在x,y方向及横滚角φ和俯仰角θ的随动跟踪中都有微小的超调产生。



图4 飞行器姿态角跟踪曲线Fig.4 Attitude angel tracking of quadrotor
3.3 抗扰动性能对比
为进一步比较两种算法抗扰动能力强弱,在t=10 s的时候,分别向控制器加入周期为20 s,脉宽为1 s,幅值为1的脉冲干扰,两种控制器的抗扰动性能对比如图5、图6所示。
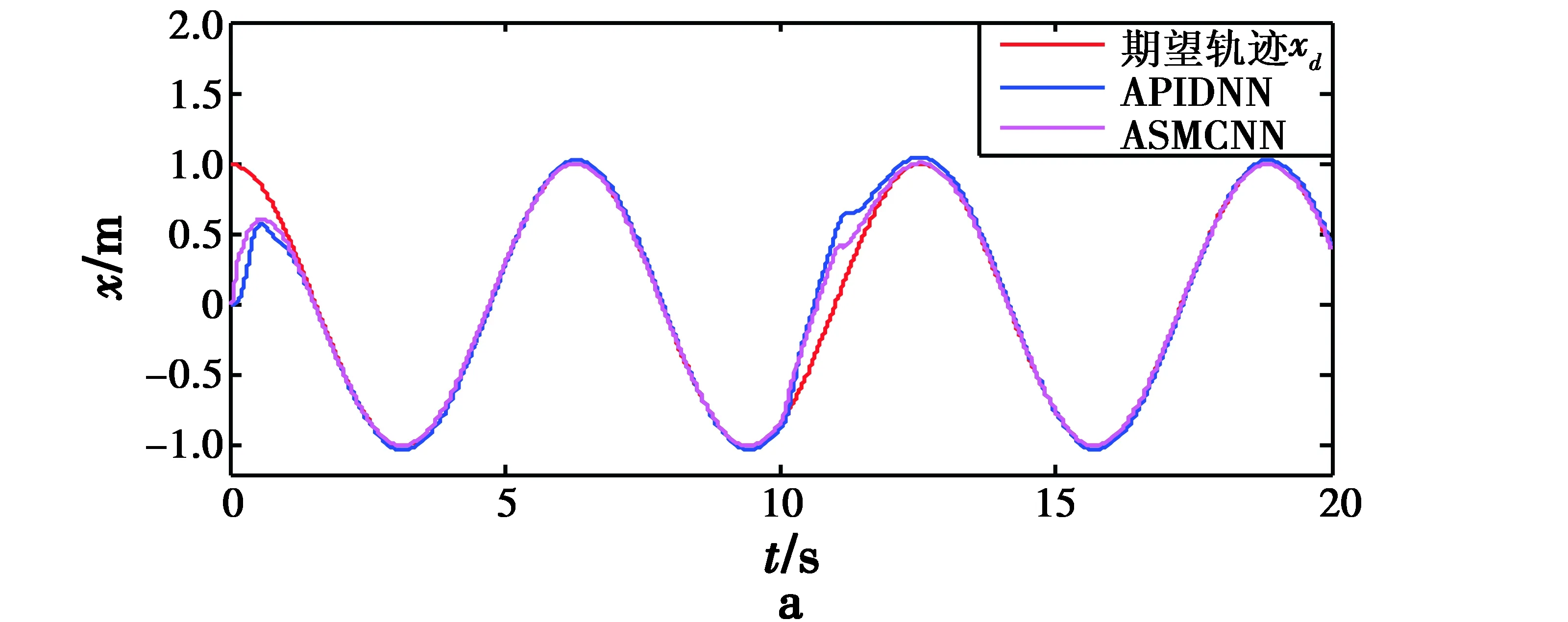
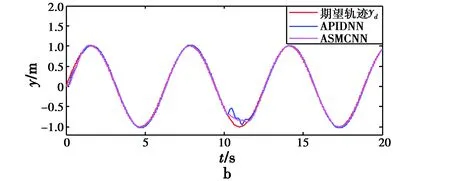

图5 扰动下飞行器位置跟踪曲线Fig.5 Position tracking of quadrotor under disturbance
由图5和图6可以看出,两种控制器都有一定的抗干扰性能,相同的外界扰动作用下,RBF网络自适应滑模控制器的幅度变化更小,且恢复速度更快,RBF网络自适应滑模控制器抗干扰能力更强。


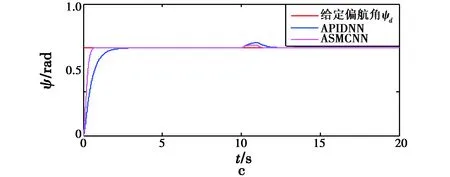
图6 扰动下飞行器姿态角跟踪曲线Fig.6 Attitude angel tracking of quadrotor under disturbance
3.4 鲁棒性能对比
在第10 s时使飞行器质量增加30%,通过飞行器高度变化验证控制器的鲁棒性能。
由图7可以看出,当飞行器质量发生突变时,RBF网络自适应滑模算法的下降幅度约为0.55 m,调整时间为2.5 s。而RBF网络自适应PID控制算法下降幅度约为0.8 m,调整时间约为3.8 s。因此RBF网络自适应滑模控制算法的鲁棒性要强于RBF网络自适应PID控制算法。

图7 参数变化下性能对比Fig.7 Experiment results when parameters changed
4 结论
针对带有不确定性的四旋翼飞行器系统,利用滑模控制对含不确定性非线性系统的鲁棒控制和神经网络自学习能力,提出一种RBF网络自适应滑模控制方法。仿真结果证明,相对于RBF神经网络自适应PID控制,本文方法具有调整时间短、超调量小、抗干扰性能优,鲁棒性能强的优点。
[1] XIONG J J,ZHENG E H.Position and attitude tracking control for a quadrotor UAV [J].ISA Transations,2014, 53(3):725-731.
[2] 江杰,冯旭光,苏建彬.四旋翼无人机仿真控制系统设计[J].电光与控制,2015,22(2):27-30.
[3] LEE D B,NATARAJ C,BURG T C,et al.Adaptive tracking control of an underactuated aerial vehicle[C]//American Control Conference(ACC),San Francisco,IEEE, 2011:2326-2331.
[4] DAS A,LEWIS F,SUBBARAO K.Backstepping approach for controlling a quadrotor using Lagrange form dynamics [J].Journal of Intelligent and Robotic Systems,2009,56(1):127-151.
[5] LUQUE-VEGA L,CASTILLO-TOLEDO B,LOUKIANOV A G.Robust block second order sliding mode control for a quadrotor[J].Journal of the Franklin Institude,2012,349(2):719-739.
[6] GUIHERME V,MANUEL G,FRANCISCI R.An integral predictive /nonlinearH∞control structure for a quadrotor helicopter[J].Automatica,2010,46(1):29-39.
[7] 李砚浓,李汀兰,姜艺,等.基于RBF神经网络自适应PID四旋翼飞行器控制[J].控制工程,2016,23(3):378-382.
[8] 刘志军,吕强,王东来.小型四旋翼直升机的建模与仿真控制[J].计算机仿真,2010,27(7):18-20.
[9] 刘金琨,郭一.柔性关节机器人自适应神经网络动态面控制[C]//第三十三届中国控制会议论文集(F卷),2014:8764-8768.
[10] 张建明,邱联奎,刘启亮.四旋翼飞行器姿态的自适应反演滑模控制研究[J].计算机仿真,2015,32(3):42-47.
[11] BERTRAND S,GUENARD N,HAMEL T,et al.A hierarchical controller for miniature VTOL UAVs:design and stability analysis using singular perturbation theory[J].Control Engineering Practice,2011,19(10):1099-1108.
RBFNeuralNetworkAdaptiveSlidingModeControlforQuad-rotorAerialVehicle
HAN Ye-zhuang, HUA Rong
(School of Electrical and Electronic Engineering,Shanghai Institute of Technology,Shanghai 201418,China)
In view of the uncertainty about the quad-rotor aerial vehicle system,a new control method is proposed by combining sliding mode control with the adaptive neural network.Considering the existing uncertainties in the actual system,such as inaccurate modeling and unknown parameters,and based on the sliding mode control,we constructed a RBF neural network to on-line approach the unknown functions of the system model,and designed an adaptive law to on-line estimate the weights of the neural network and the unknown parameters using the Lyapunov method.The stability of the system was verified by Lyapunov theorem.The simulation results show that:compared with the adaptive PID controller of the RBF neural network,this controller has a shorter settling time,less overshoot and better resistance to disturbances,and it also has a stronger robustness when the model parameters are changed.
quad-rotor aerial vehicle; sliding mode control; neural network; adaptive law
韩业壮,华容.四旋翼飞行器的RBF 网络自适应滑模控制[J].电光与控制,2017,24( 11) : 22-27.HAN Y Z,HUA R.RBF neural network adaptive sliding mode control for quad-rotor aerial vehicle[J].Electronics Optics & Control,2017,24( 11) : 22-27.
2017-03-06
2017-04-13
上海市重点课程建设项目(33210M161019)
韩业壮(1991 —),男,河北邢台人,硕士生,研究方向为四旋翼飞行器的导航与控制。
V249.1
A
10.3969/j.issn.1671-637X.2017.11.005

