四旋翼飞行器姿态的显式模型预测控制
王 仑, 苏 敏, 杨 帆, 佃松宜
(四川大学电气信息学院,成都 610065)
四旋翼飞行器姿态的显式模型预测控制
王 仑, 苏 敏, 杨 帆, 佃松宜
(四川大学电气信息学院,成都 610065)
针对四旋翼飞行系统的多变量、强耦合和带约束等复杂特性,提出了基于显式模型预测的控制方法。首先根据四旋翼飞行系统的动力学特点,建立了九状态空间模型,并解耦成2个子系统。然后,采用多参数二次规划法,离线计算了四旋翼飞行系统的显式最优控制律,在线查找当前状态对应的控制量。数值仿真和实验结果表明,该方法在满足约束条件同时,调节时间较短,超调量较小且具有一定的抗扰动能力,成功实现了四旋翼飞行器的姿态稳定控制。
四旋翼飞行系统; 显式模型预测控制; 状态空间模型; 多参数二次规划
0 引言
四旋翼飞行器是模拟直升机控制而研制的高阶、非线性、强耦合实验平台,适合实时飞行仿真和控制算法验证[1]。近年来,直升机的分析和控制得到了广泛的关注和重视[2],文献[3]采用经典的PID方法实现了四旋翼飞行器姿态角控制,但PID控制响应速度慢、控制精度较低;文献[4]基于Backstepping实现了四旋翼飞行器系统的控制器设计的目的,但其抗扰能力不强,且对初始条件要求较高;文献[5]基于输出调节理论和信号补偿方法,设计了系统的状态反馈鲁棒控制器,该方法考虑了直升机系统中存在的不确定性和外部干扰,但控制器阶数较高,不易实现;文献[6]采用线性二次调节器(LQR),解决了直升机模型的姿态飞行稳定问题,但未考虑系统存在输入输出受限的情况。
模型预测控制(MPC)是处理带约束多变量最优控制问题最有效的方法之一,已经广泛应用于石油和化学工业系统,并取得巨大的经济和社会效益[7]。文献[8]采用模型预测算法,解决了飞行器姿态控制中存在的驱动电机、系统状态和输出带约束的问题,但在实际快速系统中难以应用;文献[9]针对高超声速飞行器不确定性特点,结合滑模和预测控制方法的优点,解决了系统带约束的问题,同时克服了常规滑模的抖振现象,但其调节时间较长;文献[10]针对飞行器模型中存在的不确定和干扰失配问题,提出了基于非线性干扰观测器的广义预测控制方法,但该方法在线辨识时间较长;文献[11]采用鲁棒预测控制方法,考虑了输入受限的高超声速飞行器非线性纵向运动模型的控制问题,该方法在保证系统控制性能和稳定性的同时还降低了系统的保守性,但该方法运算过程较为复杂。
针对上述文献提到的问题,本文提出了显式模型预测控制(Explicit Model Predictive Control,EMPC)的方法应用于四旋翼飞行器姿态控制。该方法通过引入多参数二次规划 (Multi-Parametric Quadratic Programming,MPQP)来代替重复的滚动优化,离线计算每个状态分区上的状态反馈最优显式控制律,大量缩短系统在线计算时间,因此该方法适用于带约束的快速系统[12]。目前EMPC主要停留在理论研究部分,基于该方法的实际应用较少,本文成功地将EMPC应用于四旋翼飞行器姿态角控制。另外,对四旋翼飞行器姿态建模时,选择其九状态空间模型,并将其解耦为2个子系统。与现有采用的六状态空间模型相比,由于加入了3个姿态角的积分环节,因此解耦后九状态空间模型在大量减少控制器计算量的同时,提高了控制精度,可以有效消除稳态误差。通过仿真验证,成功地将EMPC和解耦后的九状态空间模型应用于实际系统,并取得较好的控制效果。
1 四旋翼飞行系统的九状态空间模型
近年来小型无人机在国内外一直是研究和开发的热点。本文研究的对象是重庆固高公司生产的四旋翼飞行仿真器,该技术平台是一个四输入三输出的对象。系统输入是4个电机的输入电压,输出为其3个姿态角。四旋翼飞行仿真器由4个螺旋桨及电机、电滑环、基座、安装盘、万向节、编码器和数据采集卡等组成[1]。
建立如图1所示四旋翼飞行器的坐标系,图中的Ff,Fl,Fr和Fb分别表示螺旋桨1,2,3,4号电机旋转时空气对四旋翼飞行器的作用力。四旋翼飞行器姿态具有3个自由度,分别为俯仰角P、滚动角R、偏航角Y[13]。

图1 四旋翼飞行器的坐标系Fig.1 The coordinate system of quad-rotor aerial vehicle
针对四旋翼飞行器的复杂特性,为建立其物理模型,在此做如下假设[1]。
1) 四旋翼飞行器的结构是完全左右对称的,其重心位于x轴上。
2) 四旋翼飞行器受到各旋翼作用力Fx(x=f,l,r,b)与其对应电机的旋转速度成正比;电机的旋转速度与电机的输入电压成正比,并忽略存在的空气阻力以及摩擦力。
3) 由于俯仰角主要受Ff,Fl,Fr3个力的影响;滚动角主要受Fr和Fl2个力的影响;偏航角只受Fb的影响,因此假设各角度只受其对应力的影响。
建立俯仰角、滚动角、偏航角力矩平衡方程为[1]
(1)
式中:Kfc为电压升力比;L1为4号螺旋桨中心到y轴的距离;Lp为1号螺旋桨中心到z轴的距离;JP,JR,JY分别为俯仰角、滚动角、偏航角转动惯量;Uf,Ul,Ur,Ub分别为螺旋桨1,2,3,4号电机电压。为了保证系统静平衡,在1号螺旋桨臂上增加了配重m1,其位置如图1所示。物理参数值如表1所示,参数来自四旋翼飞行仿真器[1]。
代入各数值并化简可得

(2)

表1 四旋翼飞行仿真器物理参数
根据假设3),螺旋桨1,2,3号电机只影响俯仰角和滚动角;4号电机只影响偏航角。因此可以把该系统解耦成两个子系统,分别记为系统1和系统2。选取俯仰角、俯仰角速度、俯仰角的积分、滚动角、滚动角速度、滚动角的积分为状态量,1,2,3号电机电压为输入量,建立俯仰角、滚动角的状态空间模型(系统1)为
(3)
式中:
选取偏航角、偏航角速度、偏航角的积分为系统状态量,4号电机电压为系统输入量,建立偏航角的状态空间模型(系统2)为
(4)

2 离线计算
显式模型预测控制引入MPQP解决约束最优控制问题,对状态空间进行凸划分并将隐式的闭环MPC系统等价转换为显式的PWA系统,因此最优控制序列和MPC系统的显式关系式由离线优化得到,不需要反复地在线优化计算[14-16]。
考虑如下约束最优控制问题

(5)
式中:U[,…,]′为最优控制序列,即决策向量;N为预测时域,定义T∈Rn为所有x(0)的可行域,xN∈Tset为终端约束集,且Τset为凸集。Q=QT≥0,R=RT>0,P≥0分别为状态、输入和输出权值矩阵。E,L,M分别是控制输入、状态和输出的约束,由实际问题确定其取值。
由于xk+1的控制模型为线性的,因此可得

(6)
将式(5)代入式(6),带约束的最优控制问题可以转化为如下最优问题[14]。
(7)
s.t.GU≤W+Ex(0) 。
初始状态x(0)决定最优序列U,若将初始状态x(0)作为最优问题的参数变量,能够避免最优问题重复在线计算,由此推出最优问题的MPQP,U和x(0)之间的显式表达式满足如下条件[14]。
在式(7)的MPQP问题中,H>0,可行域Τ= {x∈Rn|Lx≤K}为凸集,且最优控制序列U为x(0)的分段仿射(Piece-Wise Affine,PWA)函数。
U=Fix(0)+Gix(0)∈CCR i
(8)
式中:CCR i={x∈Rn|Lix≤Ki}是T的凸划分,即CCRi∪CCR j=T,CCR i∩CCR j=φ(i≠j),i,j=1,…,Nk,Nk为状态区域分区的数量,矩阵L,K,Fi,Gi和Li,Ki,Nk由求解式(7)MPQP问题得到。将式(5)系统离散化,记离散时间常数为k,系统状态为x(k),那么显式控制量u(k)是关于x(k)的PWA函数,形式为[16]
u(k)=fix(k)+gix(k)∈CCR i
(9)
式中:fi,gi分别为Fi,Gi的首行[12]。
3 数值仿真
3.1 离线控制器设计
通过对四旋翼飞行器各物理量测量与分析,可以得到各角度的约束范围以及电机电压最大值[13]。其他参数通过多次仿真设定如下。
对系统1,设定采样时间为0.03 s,状态约束为-(203020153020)T≤x1≤(203020153020)T,输入约束为-(6.777)T≤u1≤(6.777)T,状态加权矩阵为diag(30.50.00140.50.001),输入加权矩阵为三阶单位矩阵,预测时域为4。
对系统2,设定采样时间为0.03 s,状态约束为-(1003020)T≤x2≤(1003020)T,输入约束为-6.4≤u2≤6.4,状态加权矩阵为diag(30.40.001),输入加权矩阵为单位矩阵,预测时域为4。
离线计算得到系统1,2控制分区如图2所示。

图2 控制分区图Fig.2 Control partition
其中,系统1的控制分区为73个,系统2分区为7个,系统分区总个数为80个。当系统未解耦时,可求得控制分区为511个,因此解耦后的系统将控制分区减少了421个,极大地减小了计算量。
在线算法通过当前状态x(k),来获得其对应的状态分区CCRi,根据式(9)计算得到其对应的显式控制器。本文在线算法采用直接查找法,由于四旋翼飞行系统解耦后,状态分区较少,因此直接查找法即可满足控制器设计要求。
3.2 数值仿真
为验证本文EMPC控制器性能,数值仿真及实验加入文献[6]中LQR控制方法与本文采用的EMPC方法比较,且同时使用九状态空间模型。设定四旋翼飞行器俯仰角、滚动角、偏航角分别为9°,-8°,-10°,控制目标为使其分别调节到零值,仿真时间为30 s。仿真结果如图3所示。

图3 系统状态调节曲线(数值仿真)Fig.3 The regulation curves of system state(numerical simulation)
从图3可以看出,在调节到稳态过程中,LQR控制器控制的3个姿态角在6 s左右到达稳态值,且调节过程会存在一定的超调量;EMPC控制器控制的3个姿态角均在3 s左右到达稳态值,且无超调量。在15 s时对3个姿态角分别加入一个阶跃扰动,使3个姿态角产生相应的变化。从图3中可得出,在遇到扰动时,EMPC控制器相比于LQR控制器,3个姿态角能更快回到平衡位置,并无超调量。因此,从仿真结果可以看出,EMPC控制各姿态角有更好的快速性和抗扰动性。
4 实验结果
4.1 调节实验
本文实验对象为固高公司生产的四旋翼飞行仿真器。四旋翼仿真器连接计算机,在该产品自带的Matlab环境下进行控制器设计。计算机通过数据采集卡获得各旋翼上编码器计数值,并计算控制电压,用实时控制软件对飞行器进行姿态的实时控制。设定四旋翼飞行器初始俯仰角、滚动角、偏航角分别为12°,-10°,-16°,控制目标为调节各姿态角到零值,实验时间为40 s。EMPC与LQR控制四旋翼飞行器的实验结果如图4和图5所示。
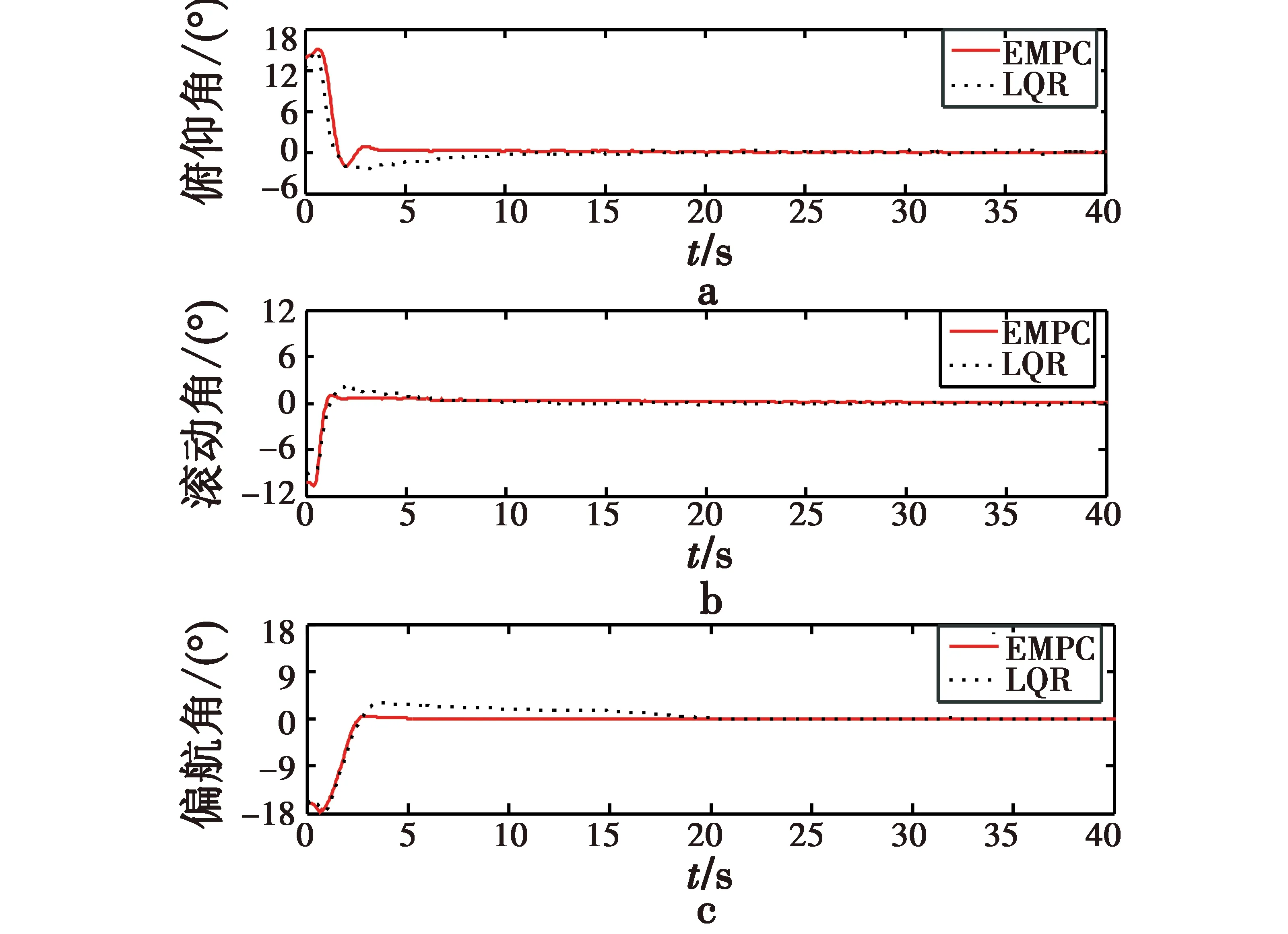
图4 系统状态调节曲线(姿态角)Fig.4 The regulation curve of system state(attitude angle)


图5 控制输入变化曲线Fig.5 System control input curves
从图4、图5可以看出,使用九状态控制模型可以消除误差,精确调节到指定角度。LQR控制3个姿态角在10 s左右达到稳定状态,且产生较大超调,到达稳态后振动频率较大,4个电机控制电压超过约束范围,需要对电压限幅;EMPC控制在满足约束条件下,调节时间为4 s,基本无超调量,到达稳态后波动更小。
4.2 扰动实验
在四旋翼飞行器到达稳态后,大约6 s时手动给四旋翼飞行器一个扰动,使3个角度均产生一定变化,并与LQR控制的3个姿态角做比较。控制目标为回到初始零位,实验时间为40 s,其调节曲线如图6所示。

图6 系统状态调节曲线(扰动实验)Fig.6 The regulation curve of system state(perturbation experiment)
从实验结果可以看出,在遇到扰动时,九状态模型仍然可以消除稳态误差。LQR控制3个姿态角在调节10 s后达到稳定状态,但超调量较大,到达稳态后存在一定波动。而EMPC控制的3个姿态角在遇到扰动时,调节时间为4 s,超调量较小,在稳定后具有较小的波动值,因此具有较好的抗扰动能力。
5 结束语
针对带约束的多输入多输出四旋翼飞行器快速系统,提出了基于显式模型预测控制的方法。首先建立四旋翼飞行系统的九状态空间模型,并将其解耦成2个子系统,有效减少计算量,提高控制精度。仿真与实验验证了基于九状态空间模型实施显式模型预测控制方法在四旋翼飞行系统姿态控制中的可行性和有效性。
[1] 罗倩兰.基于RBF-ARX模型的预测控制在四旋翼飞行器控制系统中的应用[D].长沙:中南大学,2012.
[2] KUTAY A T,CALISE A J,IDAN M,et al.Experimental results on adaptive output feedback control using a labora-tory model helicopter[J].IEEE Transactions on Control Systems Technology,2005,13(2):196-202.
[3] LU X H,LI J B,LIU W J.A study of complementary filter algorithm for four-rotor helicopters attitude control system[J].Sensors & Transducers,2014,174(7):298-306.
[4] 赵元伟,卢京朝.四旋翼飞行器的建模及基于反步法的控制[J].科学技术与工程,2013,13(34):10425-10430.
[5] ZHENG B,ZHONG Y S.Robust attitude regulation of a 3-DOF helicopter benchmark:theory and experiments[J].IEEE Transactions on Industrial Electronics,2011,58(2): 660-670.
[6] KUMAR M V,SAMPATH P,SURESH S,et al.Design of a stability augmentation system for a helicopter using LQR control and ADS-33 handling qualities specifications[J].Aircraft Engineering and Aerospace Technology,2008,80(2):111-123.
[7] 席裕庚,李德伟,林姝.模型预测控制——现状与挑战[J].自动化学报,2013,39(3):222-236.
[8] 盖俊峰,赵国荣,周大旺.刚体飞行器姿态机动的模型预测控制方法[J].弹箭与制导学报,2015,35(2):5-9.
[9] 高海燕,蔡远利.高超声速飞行器的滑模预测控制方法[J].西安交通大学学报,2014,48(1):67-72.
[10] 孙光,朱如意,王征.基于干扰观测器的飞行器再入姿态广义预测控制[J].航天控制,2016,34(4):10-15.
[11] 胡超芳,任艳丽,解倩倩.基于RMPC的高超声速飞行器输入饱和控制[J].航天控制,2016,34(2):20-26.
[12] 张聚.显式模型预测控制理论与应用[M].北京:电子工业出版社,2015.
[13] 魏吉敏.四旋翼飞行器的建模及预测控制研究[D].长沙:中南大学,2013.
[14] BEMPORAD A,MORARI M,DUA V,et al.The explicit linear quadratic regulator for constrained systems [J].Automatica,2002,38(1):3-20.
[15] PANOS C,KOURAMAS K I,GEORGIADIS M C,et al.Modelling and explicit model predictive control for PEM fuel cell systems[J].Chemical Engineering Science, 2012,67(1):15-25.
[16] HU Z,HAMEYER K.A method of constraint handling for speed-controlled induction machines[J].IEEE Transactions on Industrial Electronics,2016,63(7):4061-4072.
ExplicitModelPredictiveControlforAttitudeofQuad-rotorAerialVehicles
WANG Lun, SU Min, YANG Fan, DIAN Song-yi
(College of Electrical and Information,Sichuan University,Chengdu 610065,China)
Considering the complex characteristics of quad-rotor aerial vehicles,such as multiple variables,strong coupling and the constraints,we proposed a controlling method based on explicit model prediction. According to the dynamic characteristics of the quad-rotor flight system,a nine-state space model was built,which was decoupled into two subsystems.Then,the explicit optimal controlling law of the quad-rotor flight system is calculated offline by multi-parameter quadratic programming,and the controlled quantity corresponding to the current state was searched online. Numerical simulation and experiment results show that the proposed method has the advantages of short adjusting time,small overshoot and certain anti-disturbance ability,as well as meeting the constraint requirements,and the stability control of the attitude is successfully achieved.
quad-rotor flight system; explicit model predictive control; state space model; multi-parameter quadratic programming
王仑,苏敏,杨帆,等.四旋翼飞行器姿态的显式模型预测控制[J].电光与控制,2017,24( 11) : 53-57.WANG L,SU M,YANG F,et al.Explicit model predictive control for attitude of quad-rotor aerial vehicles[J].Electronics Optics & Control,2017,24( 11) : 53-57.
2016-12-14
2017-01-04
王 仑(1994 —),男,湖北孝感人,硕士生,研究方向为显式模型预测控制。
TP29
A
10.3969/j.issn.1671-637X.2017.11.011

