基于KL 距离的异类传感器动态数据关联算法
吕丽平, 白 鑫, 张玉宏
(1.郑州升达经贸管理学院信息工程系,郑州 451191; 2.河南工业大学信息科学与工程学院,郑州 451000)
基于KL 距离的异类传感器动态数据关联算法
吕丽平1, 白 鑫1, 张玉宏2
(1.郑州升达经贸管理学院信息工程系,郑州 451191; 2.河南工业大学信息科学与工程学院,郑州 451000)
针对异类传感器多目标跟踪系统中的动态数据关联问题,提出了一种基于KL距离的异类传感器动态数据关联算法。该方法将静态多维分配问题推广到动态跟踪中,通过对量测集合与航迹集合的合并,将各传感器量测估计位置的概率密度函数与目标航迹一步预测值的概率密度函数之间的KL距离作为关联代价函数,继而代入多维分配模型求解,从而实现量测到航迹的动态关联。仿真实验表明,所提算法能更精准地反映量测与航迹之间关联的可能性,且能够对多目标进行快速稳定的跟踪。
数据关联; 多目标跟踪; 粒子滤波; KL距离
0 引言
数据关联问题一直是目标跟踪融合系统中最重要、最困难的研究内容,而现今已有的数据关联算法多是针对主动传感器提出的。文献[1]提出了一种新的2-D分配算法,用来解决一对多或多对一的分配问题。这个问题的解决,突破了一对一分配的限制,使得最近邻、联合概率数据互联、多假设等典型的数据关联算法都可以归结为多维分配的问题,然而多维分配问题存在一个缺陷即NP问题。目前解决该问题大致可以分为3种思路:1) 寻找解决多维分配问题的启发式算法,即利用解析性的启发式算法[2]或者借助群智能理论对全关联空间进行概率搜索[3-4];2) 提取、利用先验信息对多维分配问题进行降维,通过设定关联规则来设置空间的禁忌搜索区域[5-6];3) 增强数据关联模型的完备性[7-9]。以上基于多维分配的算法均只考虑同一时刻各传感器观测的互联问题,是一个静态结果,而文献[10]将基于多维分配的静态分配推广到动态跟踪中,通过对量测集合和航迹集合的合并,把S维转变为S+1维问题,从而实现了目标航迹和量测分配的动态化;在此基础上,文献[11]提出了动态多维分配算法的串行处理结构,将预关联的量测集和航迹进行关联;文献[12]则提出了一种综合动态多维分配和两级式处理结构的串行数据关联算法。然而以上方法均未考虑关联代价函数对动态多维分配数据关联算法关联正确率的影响问题,而是直接利用文献[10]给出的量测与伪量测之间的统计距离作为关联代价,然而由静态多维分配算法可知,关联代价的构造是动态多维分配数据关联算法的关键,直接决定了数据关联算法的性能,因此,研究关联代价函数与动态多维分配数据关联算法之间的关系具有重要的意义。
本文针对异类传感器多目标跟踪系统中的动态数据关联问题,对动态多维分配数据关联算法的关联代价函数的构造问题进行研究,以期提高多目标动态跟踪的精度和效率,仿真实验验证了所提算法的有效性和可行性。
1 问题描述
不失一般性,本文以N部能测距和测角的主动传感器和M部仅测角的被动传感器组成的异类传感器融合系统同步扫描探测为例,考虑漏检和虚警,建立了异类传感器目标跟踪模型。图1给出了异类传感器协同观测模型示意图(N=2,M=2)。

图1 异类传感器协同观测模型Fig.1 The cooperative observation model of heterogeneous sensors
主动传感器s获得目标j的量测为距离r1j,方位角βsj和俯仰角αsj,分别表示为[7]
(1)
记向量Zsj=(rsjαsjβsj)T,s=1,2,…,N。被动传感器s仅能获得目标j的方位角为βsj,俯仰角为αsj,分别表示为
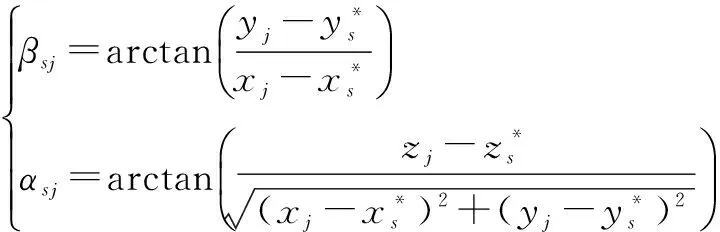
(2)
记向量Zsj=(αsjβsj)T,s=N+1,…,N+M。
综上,传感器的量测模型可表示为

(3)
式中,s=1,2,…,N+M,传感器s的ns个量测中,来自目标的量测为真实目标的位置加上高斯噪声,即vsj服从高斯分布N(0,Rsj),来自虚警的量测在空间中无规律分布,视为均匀分布,其概率密度为wsj=1/Φs(0<Φs<π2)。
为使得所有量测数据均参与关联,给每个传感器s增加一个虚假量测ms 0,则传感器s获得的量测集合可表示为
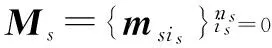
(4)
并记所有传感器获得的量测数据为
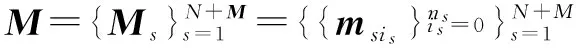
(5)

2 基于KL距离的动态数据关联算法
与静态数据关联不同[7-9],在动态数据关联过程中,需要进行航迹滤波,通过航迹的不断更新可以获得目标在各个时刻的位置及协方差估计,并且能够获得目标的状态预测值和预测协方差矩阵,因此,在该数据关联过程中,可利用目标的航迹信息构造候选关联组合,通过将量测集合和目标的航迹集合合并,把S维问题转变为S+1维问题,从而实现量测与航迹的动态分配[10]。
为实现目标的动态跟踪,须将量测与目标航迹建立联系。将k时刻来自N+M个传感器的量测集合M(k)与k-1时刻系统的目标航迹集合U(k-1)合并,表示为

(6)
对MU进行划分时,会产生一系列量测-航迹对Mi1i2…iN+M(k)Xjk-1|k-1构成的候选关联组合。图1给出了传感器量测与目标航迹构成的不同候选关联组合示意图N=2,M=2,区域1(由虚线组成)和区域2(由实线组成)分别对应着2个正确的候选关联组合。候选关联组合中量测与航迹相关性的衡量方法影响着数据关联算法的关联正确率,继而影响着跟踪算法的滤波精度。
对于由量测与航迹构成的候选关联组合,可采取多种方法来衡量其相关性。文献[10]利用航迹一步递推得到预测量测,继而利用量测与预测量测之间的统计距离来衡量其相关性。而文献[13]利用量测最小二乘估计出目标的位置,然后利用其与航迹一步递推得到的目标预测位置之间的统计距离来衡量其相关性。对候选关联组合分析可知,对来自传感器的量测,利用最小二乘算法可以获得目标位置的概率密度函数,对目标航迹进行一步递推可得到目标预测位置的概率密度函数,而概率密度函数之间的距离也是衡量两者之间相关性的一个方法。KL距离在最大似然意义上是最优的相似性测度,由其构建的关联代价更能精确地反映量测和伪量测之间的相似性。因此,本文采用估计目标位置的概率密度函数和预测目标位置概率密度函数之间的KL距离来衡量候选关联组合中量测与航迹之间的相关性,即针对候选关联组合(M1i1(k),M2i2(k),…,M(N+M)iN+M(k),Xjk-1|k-1)T,首先将来自N+M个传感器的量测值M1i1(k),M2i2(k),…,M(N+M)iN+M(k)利用最小二乘算法估计出目标位置的均值和协方差矩阵,然后通过滤波算法对航迹进行一步递推,获得k时刻目标位置的预测值和相应的协方差矩阵,最后利用两个概率密度函数之间的KL距离来衡量关联组合的相关性。
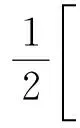
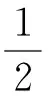
(μi-μj)-2d]
(7)
式中,d表示目标位置的维数。
则量测源M(k)来源于目标Xjk-1|k-1的似然函数为
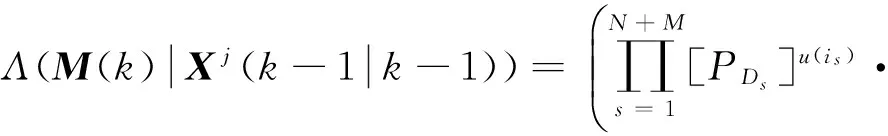
(8)
式中:PDs为检测概率;u(is)为二值函数,当is=0时,u(is)=0,否则,u(is)=1。
为了涵盖新目标出现的情况,在已形成目标航迹的集合中增加一个假目标X0,则目标的航迹表示为

(9)
因此,量测源M(k)来源于目标Xjk-1|k-1的似然函数修正为
Λ(M(k)|Xj(k-1|k-1))=
(10)
则其对应的代价函数为
(11)
定义二进制变量,ρi1…ijs则极小化负对数似然比形成了如下的广义S+1维分配问题
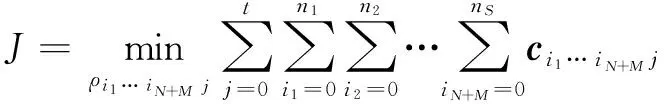
(12)
约束条件表示为
对于由主动传感器和仅测角被动传感器组成的异类传感器跟踪系统而言,由于被动传感器获得的量测是关于目标的角度信息,量测与目标状态之间的强非线性关系使得无法利用量测信息对目标的状态分布进行充分描述。针对此问题,本文采用基于Sigma点的H∞拟蒙特卡罗粒子滤波[14]进行多目标的跟踪,以此来提高跟踪效率。利用Sigma点H∞滤波产生重要性函数,拟蒙特卡罗算法进行重采样,就得到了Sigma点H∞拟蒙特卡罗粒子滤波算法(SHQPF)。由于Sigma点H∞滤波对不确定观测噪声具有较强的鲁棒性,而且在滤波过程中考虑了最新的观测值,所以根据该重要性函数产生的样本更接近于真实的采样样本。本文采用并行的滤波算法来对多目标进行跟踪,跟踪流程如图2所示。
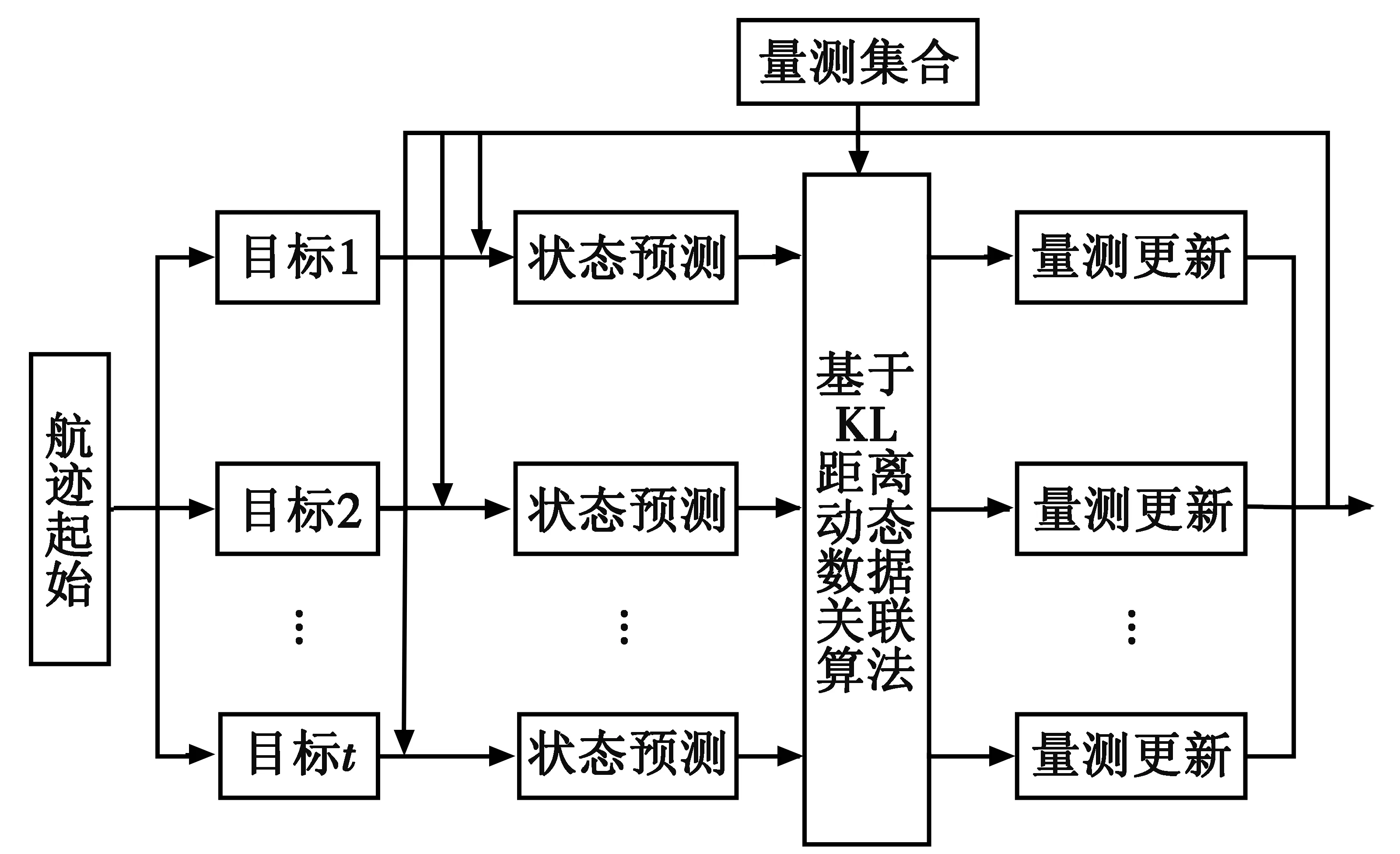
图2 多目标跟踪流程图Fig.2 Flow chart of multi-target tracking
3 仿真实验分析
为验证所提算法的有效性,将本节所提算法与文献[10]、文献[13]所提的关联代价函数用于异类传感器系统进行比较。需指出的一点是,用于数据关联的多维分配问题是一个组合优化问题,并且即使对于规模为3的情形都是NP-hard问题,在多项式时间内难以获得全局最优,因此,本节采用离线工具包LP_SOLVE来求解多维分配算法。
3.1 仿真场景设置

X(k+1)=FX(k)+Gkwk
(13)

传感器为静态的,雷达的位置坐标为(20 km,0 km,0.1 km),两个红外传感器的坐标分别为(0 km,20 km,1 km)和(0 km,0 km,0.5 km),设定传感器的采样周期为T=1 s,检测概率PD=1。雷达的量测函数方程定义为
h1(x)=(rθβ)T+v1
(14)
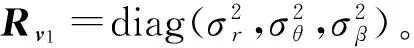
红外传感器的量测方程定位为
hs(x)=(θsβs)T+v2s=1,2
(15)
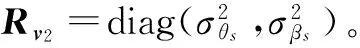
杂波数量服从参数λ=5的泊松分布,其在以目标观测预测为中心的椭球区域内服从均匀分布。实验持续时间为120 s,蒙特卡罗实验次数为500,粒子数为500。实验分别考察算法在不同传感器量测误差情况下的关联正确率和算法的性能。
3.2 实验结果及分析
相对于雷达来说,红外传感器具有较高的测角精度,因此,设定红外传感器的方位角误差标准差为σθ、俯仰角误差标准差均为σβ,雷达的方位角误差标准差为1.5σθ、俯仰角误差标准差均为1.5σβ、测距误差标准差为σγ,下面给出算法的滤波结果。
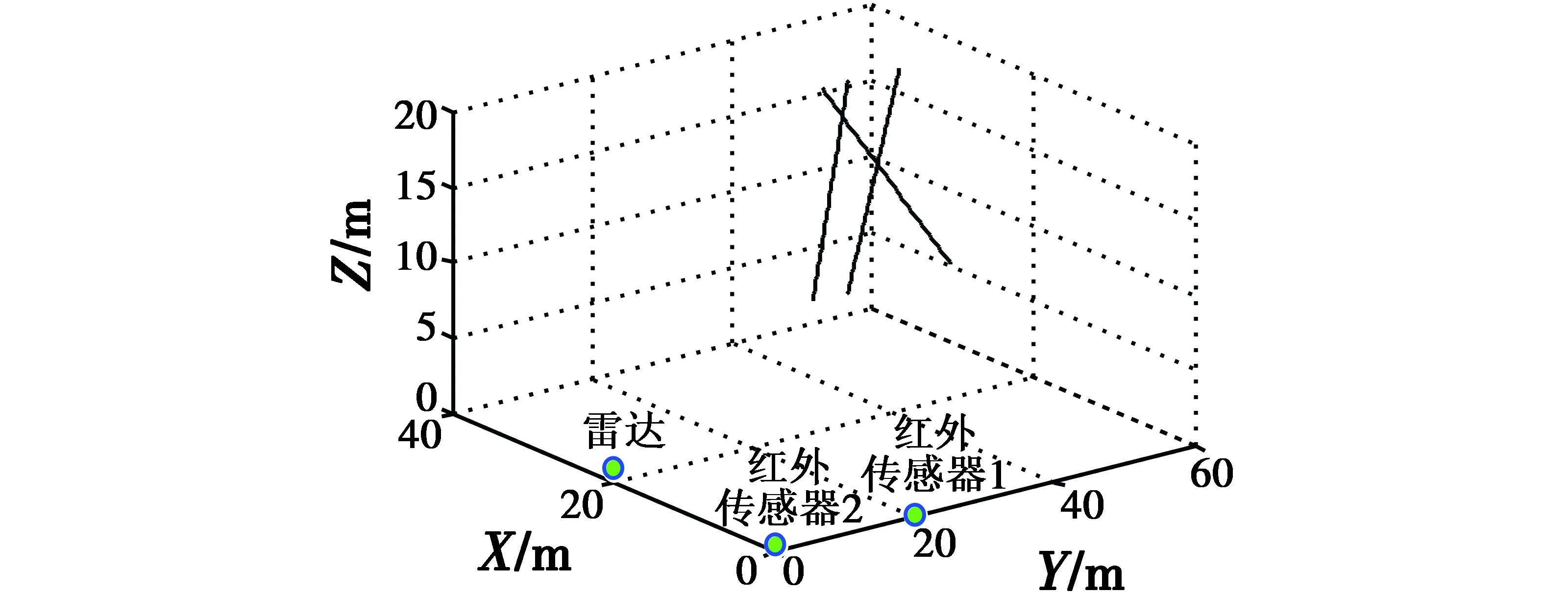
图3 目标运动真实轨迹图Fig.3 The real target trajectory
图3为3个目标的运动轨迹图。表1~表3给出了进行100次蒙特卡罗仿真时,3种算法在不同测角误差σβ1,σβ2,σθ1,σθ1和不同测距误差σγ情况下的平均关联正确率变化情况。
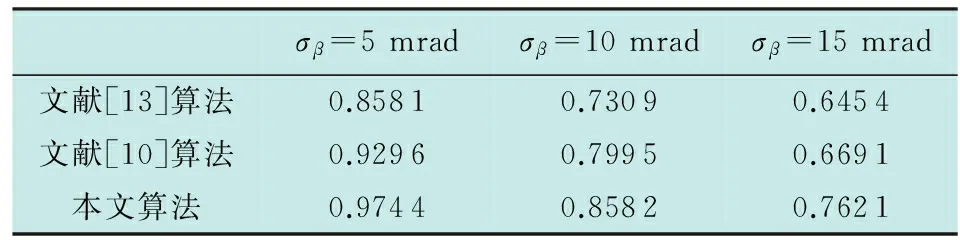
表1 3种算法在不同测角误差σβ下的关联正确率(σγ=100 m,σθ=10 mrad)
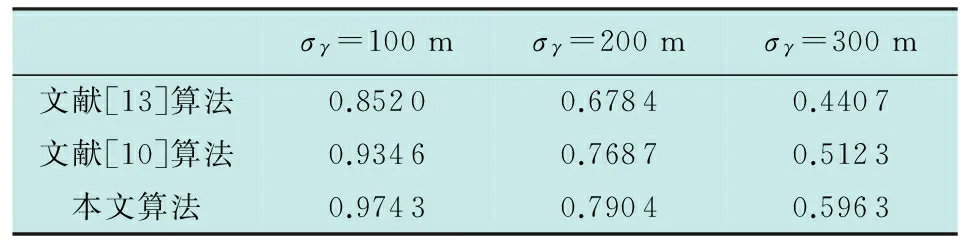
表2 3种算法在不同测距误差σγ下的关联正确率 (σβ=5 mrad,σθ=10 mrad)
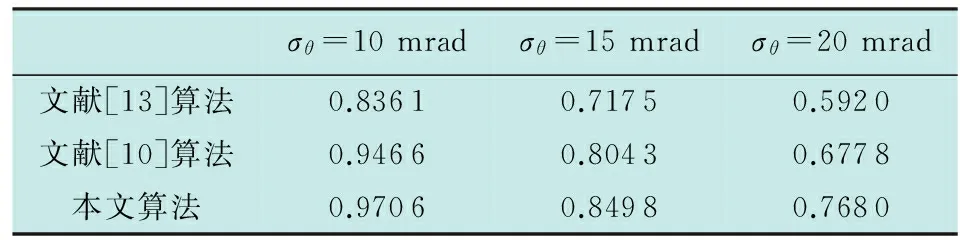
表3 3种算法在不同测角误差σθ下的关联正确率(σγ=100 m,σβ=5 mrad)
从表中可以看出,随着量测误差的增大,各算法的关联正确率逐渐降低,这主要是由于量测误差会显著影响算法的定位精度,从而导致关联代价出现偏差,降低关联正确率。从3个表中可以看出,相比传感器的测角误差,关联正确率受雷达测距误差影响较大。从各算法关联正确率的统计结果来看,在相同量测误差情况下,本文算法的关联正确率要高于文献[10]和文献[13]所提算法,3种算法的正确关联率排序为:本文算法>文献[10]算法>文献[13]算法,其中,本文算法鲁棒性最强,即使在较大的量测误差情况下,关联正确率仍然能保持在75%左右,其主要原因是本文算法在构造代价函数时,考虑目标的位置估计值以及航迹一步递推值均是服从某种分布的随机变量,因此,概率密度函数之间的距离更能表征量测与航迹之间的关联度,从而可以更加贴切地表征关联代价以改善关联正确率;文献[10]所给出的算法在量测误差较小时表现良好,而在量测误差较大时其性能表现差强人意,主要原因是利用量测与航迹的量测预测之间似然函数作为关联代价,因此,在量测误差较大时,受杂波影响较严重,尤其是在密集杂波环境下,因此,该算法更适用于量测精度较高且杂波较少的场合;相比以上2种算法,文献[13]所给的算法无论在量测误差大或者量测误差小的情况下,其关联正确率均较低,其主要原因在于其关联代价函数不能精准地反映量测与航迹之间的相关性,从而导致关联正确率的降低。
图4给出了100次蒙特卡罗仿真,3种算法在不同量测误差σθ,σβ,σγ下的跟踪均方根误差。从图中可以看出,随着时间的推进,3种算法逐渐收敛,说明其均能够对运动目标进行较为稳定的跟踪,并且随着传感器的量测误差标准差的增大,跟踪误差有所增加,但跟踪均方误差均保持在较小的范围内。进一步分析,本文算法的滤波误差小于其他2种算法,且量测误差越大趋势越明显。这是由于滤波误差大小与关联正确率有直接的关系,关联正确率越高,其滤波误差越小,关联正确率越低,其滤波误差越大,因此,关联代价函数的性能对算法的滤波结果有重要的影响。


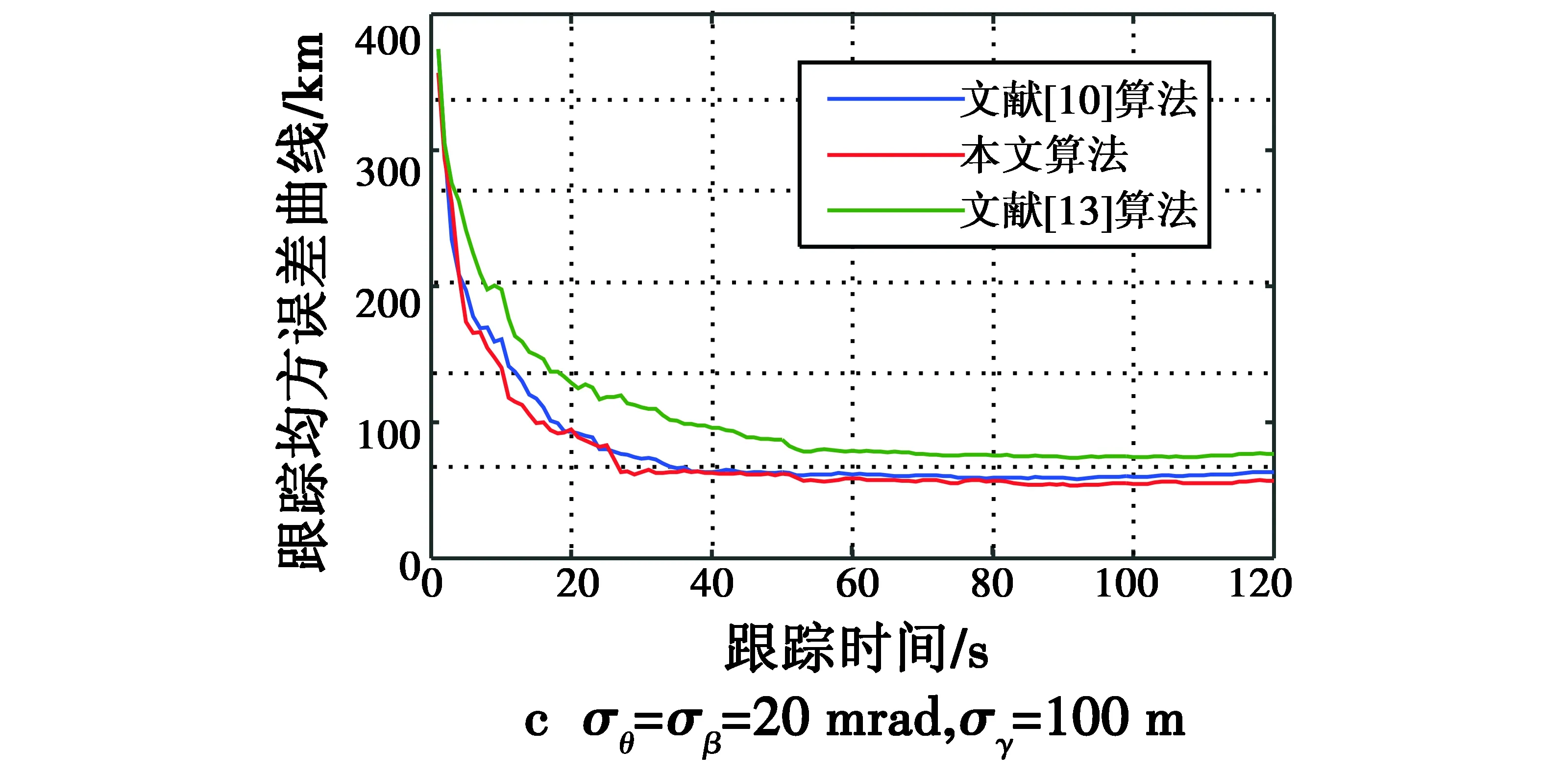
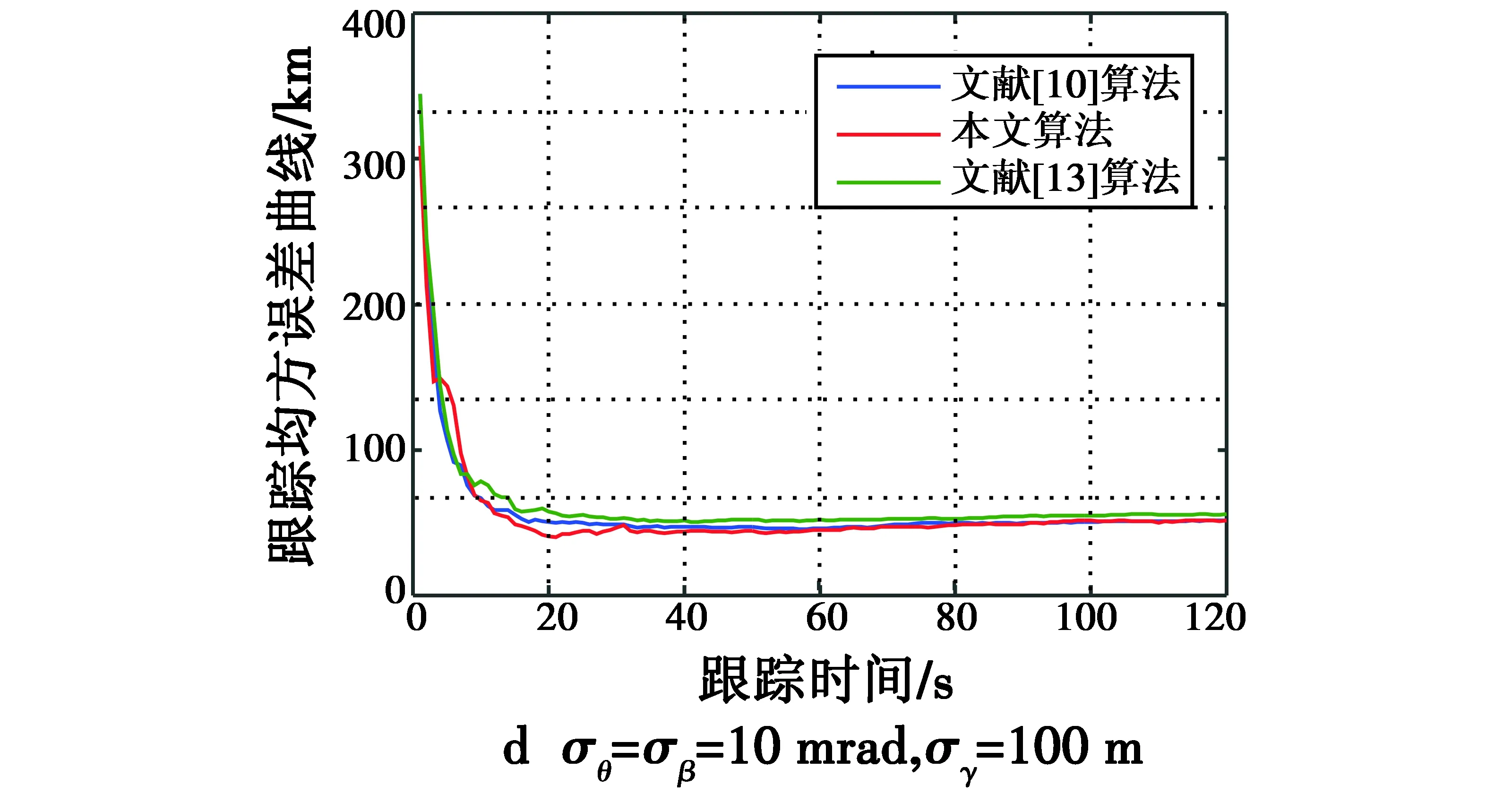
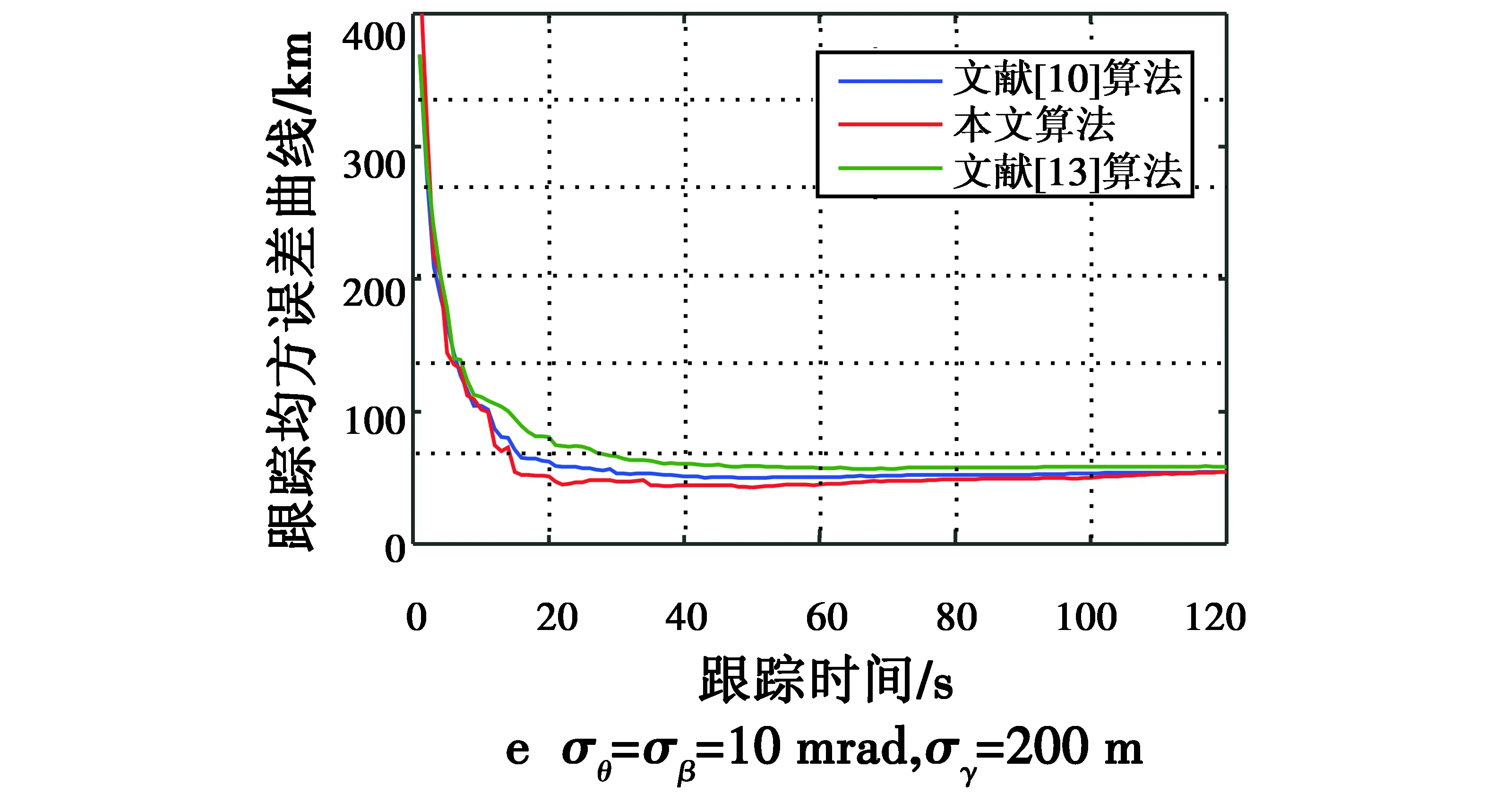
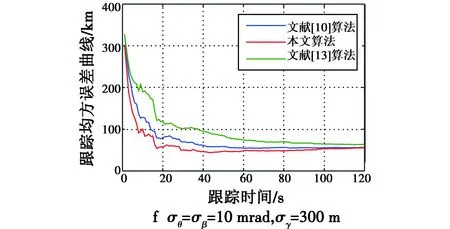
图4 3种算法在不同量测误差σθ,σβ,σγ下的跟踪均方根误差Fig.4 The RMSE of three algorithms with different σθ,σβ and σγ
4 结论
本文对三维空间中主动传感器与被动传感器组成的异类传感器多目标跟踪系统中的动态数据关联进行了研究。动态数据关联作为一个最优化问题,与静态数据关联相比多了一维,本文运用(S+1)维的多维分配算法,连接具有共同源的量测或航迹组成关联集合,将运用定位算法得出传感器量测估计的目标位置与目标的预测位置进行关联,得到全局最优的关联结果,从而更新航迹。仿真实验验证了算法的有效性和可行性。
[1] BARSHALOM Y,WILLIAM D B.Multitarget-multisensor tracking,applications and advances[M].Norwood MA:Artech House,2001.
[2] PEREA F,WAARD H.Greedy andk-greedy algorithms for multidimensional data association[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(3):1915-1925.
[3] 刘航,窦丽华,辛斌,等.基于改进单亲遗传算法的被动传感器数据关联[J].控制与决策,2008,23(4):464-468.
[4] 康莉,谢维信,黄敬雄.一种基于蚁群算法的多目标跟踪数据关联方法[J].电子学报,2008,36(3):587-591.
[5] 蒋文涛,孙利民,吕俊伟,等.面向测向交叉定位的2级消元数据关联算法[J].华中科技大学学报:自然科学版,2012,40(3):63-67.
[6] 叶西宁,潘泉,程咏梅,等.多维分配的剪枝法及其在无源探测跟踪中的应用[J].电子学报,2003,31(6):847-850.
[7] 田野,姬红兵,欧阳成.基于距离加权最小二乘的量测数据关联[J].系统工程与电子技术,2011,33(11):2353-2358.
[8] OUYANG C,JI H B,TIAN Y.Improved relaxation algorithm for passive sensor data association[J].IET Radar, Sonar and Navigation,2012,6(4):241-250.
[9] 鹿传国,冯新喜,孔云波,等.基于信息散度的多无源传感器数据关联算法[J].控制与决策,2013,28(11):1674-1678.
[10] 衣晓,何友,关欣.多目标跟踪的动态多维分配算法[J].电子学报,2005,33(6):1120-1123.
[11] 何友,衣晓,关欣.基于串行处理的动态多维分配算法[J].西安电子科技大学学报:自然科学版,2005,32(3):489-493.
[12] 熊伟,张晶炜,何友.基于S-D分配的多传感器联合概率数据互联算法[J].清华大学学报:自然科学版,2005,45(4):452-455.
[13] 惠军华.异类传感器数据关联算法研究[D].西安:空军工程大学,2013.
[14] 孔云波,冯新喜,鹿传国,等.基于Sigma点H∞滤波的拟蒙特卡罗粒子滤波算法[J].吉林大学学报:工学版,2014,44(6):1831-1837.
DynamicDataAssociationAlgorithmBasedonKLDistanceforHeterogeneousSensors
LYU Li-ping1, BAI Xin1, ZHANG Yu-hong2
(1.Department of Information Engineering,Shengda Economics Trade & Management College of Zhengzhou,Zhengzhou 451191,China; 2.College of Information Science and Engineering,Henan University of Technology,Zhengzhou 451000,China)
To solve the problem of dynamic data association in the multi-target tracking system of heterogeneous sensors,a dynamic data association algorithm for heterogeneous sensors is proposed based on KL distance.This method extends the static multi-dimensional assignment to dynamic tracking.The KL distance between the probability density function of the estimated position and the probability density function of the predicted position of the target track is taken as the association cost function,by merging the measurement set with the track set.Then,it is substituted into the multi-dimensional assignment model to realize the dynamic correlation between measurements and tracks.Simulation results show that the proposed cost function can reflect the association probability between measurements and tracks more accurately and can track multiple targets quickly and steadily.
data association; multi-target tracking; particle filter; KL distance
吕丽平,白鑫,张玉宏.基于KL 距离的异类传感器动态数据关联算法[J].电光与控制,2017,24( 11) : 43-48.LYU L P,BAI X,ZHANG Y H.Dynamic data association algorithm based on KL distance for heterogeneous sensors[J].Electronics Optics & Control,2017,24( 11) : 43-48.
2016-11-23
2016-12-05
河南省科技厅自然科学项目(152102210261)
吕丽平(1979 —),女,河南许昌人,硕士,副教授,研究方向为智能控制及计算机应用。
TN953
A
10.3969/j.issn.1671-637X.2017.11.009

