基于有限元法的水平接地体冲击接地电阻计算与分析

邱立，傅天奕，张尧，邓长征，赵自威，谢海龙，曹新阳

（1.三峡大学电气与新能源学院，湖北宜昌443002；2.湖北省三峡大学新能源微电网协同创新中心，湖北宜昌443002；3.国网湖南省电力公司株洲供电分公司，湖南株洲412000）

自然界的地闪雷电流是由雷云对地放电时的主放电过程产生的。在输电线路或杆塔本身遭受雷击时，杆塔接地装置需要把巨大的雷电流疏导到大地，以此降低杆塔本身的电位升，便能减少雷电反击跳闸事故，所以输电线路的防雷接地对于接地装置的参数要求很高[1]。

在现阶段研究杆塔冲击特性中，针对工频接地电阻的计算已经大致成形[2-3]，而想要精确地计算冲击接地电阻一直是个技术难点[4]。电感作为计算冲击接地电阻的重要参数，其传统做法是利用经验公式计算、查找以往列表[5]，或利用模拟试验的方法[6]。但是这些方法并不准确，接地装置形状、参数、土壤电阻率的变化都可能使得这些公式或列表不能适用于各种不同环境；而且公式或列表往往都没有考虑接地体互感的影响，冲击电流下的互感比工频电流下大很多，因此冲击电阻测量时不能忽略接地体间的互感[7]。而在之前仿真计算中也很少考虑雷击接地装置后导体段本身的自感和互感效应，因此仍然存在不准确性[8]。

文献[9]中提出经验公式中的电感公式是用平均电位法在各种近似条件下所得出，没有准确考虑导体的自感和互感。而文献[10-11]中分析雷电流主频分量的频率比工频高很多，因此雷电冲击下互感M比工频下大很多。文献[7]中结论指出：冲击电流下的接地体互感比工频电流下大很多，测量时需考虑互感的影响。文献[12]基于矩量法和电路理论，提出了一种考虑互感的分析接地网频域性能的数值方法，但计算过程需要大量参数和公式，不适于实际计算。文献[13]中采用ANSYS有限元计算同轴电缆的单位长度自感和互感，验证了计算接地体电感方法的可行性和准确性。

综上所述，目前学者对杆塔接地体冲击特性的研究进行了大量实验测量和仿真计算，表明了冲击电阻考虑互感的必要性，但都很少考虑或计算接地导体段的互感。如今计算机的发展推动了接地装置在冲击下电流的仿真研究，这大大地加速了冲击接地特性计算的实用性和灵活性。为此，本文采用有限元法计算得到单根水平伸长接地体段间自感和互感。基于此，能够更加方便准确地计算冲击接地电阻。

1 电感求解方程

1.1 传统经验公式

一般传统的做法是利用经验公式[14]得到导线的电阻、电感、电容和电导，以此计算水平伸长接地体的冲击接地电阻。伸长接地体按照有损长线处理下，L0表示有损导线单位长度电感，其值为

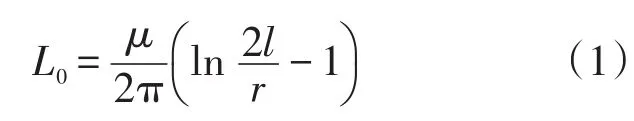
式中：l和r分别为接地体的单位长度和半径，m；μ为土壤的导磁系数，可取为4π×10-7。

1.2 ANSYS有限元原理公式

首先假设介质是线性的，那么对于单根水平伸长接地体，它的任意点磁能密度w为

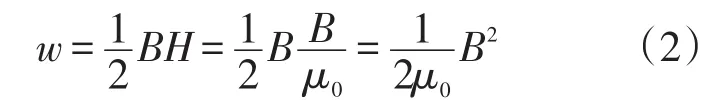
式中：B和H分别为任一点处的磁感应强度和磁场强度；μ0为空气磁导率。

在整个体积v内对磁场的磁能密度进行积分，则可得到该接地体的磁场能量

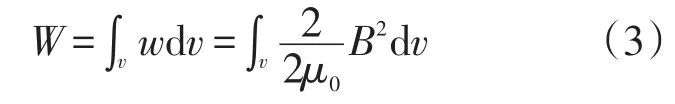
利用ANSYS有限元软件对水平伸长接地体的磁场分布进行分析。首先，将连续的空间场域进行离散化，将每个模块中的磁能密度视为常数，求出每一个单元的磁场能量且进行积分，便可求出水平伸长接地体所在区域内总的磁场能量W

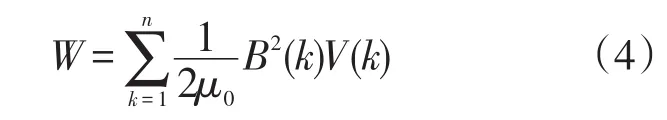
式中：n为剖分单元个数；B(k)、V(k)分别为单元k的磁感应强度和体积。

从电磁场的基础知识可知，外源在回路电流流动过程中所做的功产生了磁场能量，并且该能量存在于磁场的全部区域中。可以把伸长接地体和周围土壤看作一个回路或一个整体，则储存在伸长接地体和周围土壤所建立的磁场中的总磁场能量W为

式中：I为流过接地体的电流；L为接地体的电感值。

由式（5）可推导出水平伸长接地体电感的计算表达式为

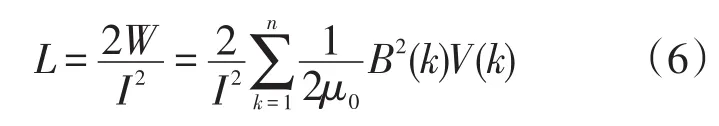
根据上述原理，采用ANSYS有限元能量法求解水平伸长接地体的总磁场能量W，就可以利用公式（6）求出对应的电感值。

图1为利用有限元商用软件包ANSYS进行计算的截面磁感应强度示意图。

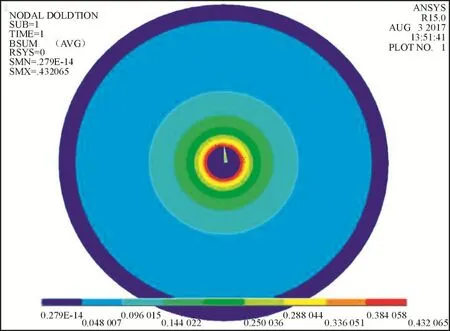
图1 接地体截面磁感应强度云图Fig.1 The magnetic induction of the grounding body section

在ANSYS后处理系统里就可以得到整个空间内的磁场能量总和。

2 仿真计算方法

2.1 互感计算模型

设想把水平伸长接地体均匀分成各段单位，如果认为接地体的各段单位是独立导体，则它们不仅各自有自感，而且它们之间还存在互感。因此基于能量摄动法和有限元能量法就能计算水平伸长接地体的单位长度自感与各单位之间的互感。

首先水平伸长接地体总的电感表达式为

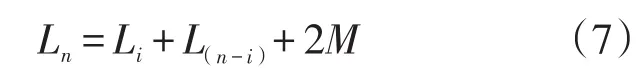
式中：Li为第i段接地体的自感；为除去第i段的接地体自感；M为第i段接地体和其余接地体的互感。

即可得到水平伸长接地体第i段的电感表达式为

图2为利用有限元ANSYS软件进行的计算接地体互感示意图，图中红色和非红色区域计算得到的电感即为公式（7）中的L（n-i）和Li。

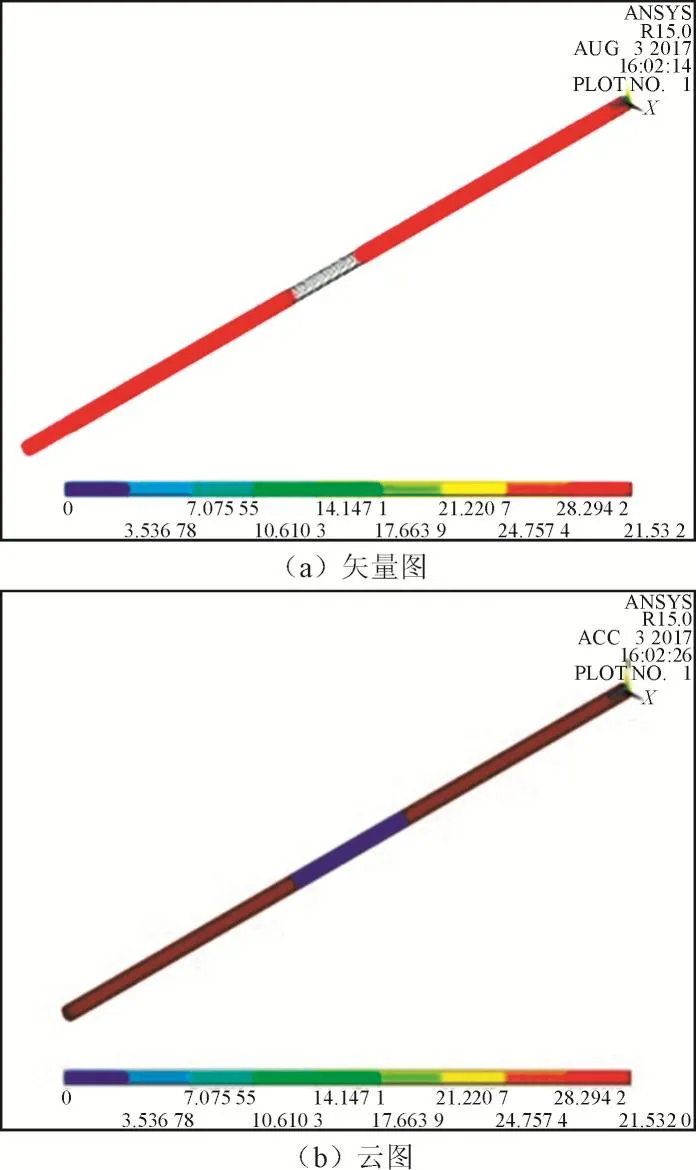
图2 互感计算模型示意图Fig.2 Schematic diagram of the mutual inductance calculation model

2.2 分布参数电路模型

为了计算冲击接地电阻，本文采用分布参数电路模型进行计算，先将水平接地体分割成5个等长单元，然后确定单位长度接地电极的参数，利用线性差分电路模型组成相应的等效电路，最后根据有损导线的分布参数公式[14]，把接地电极各个单元的参数代入该模型，见图3。

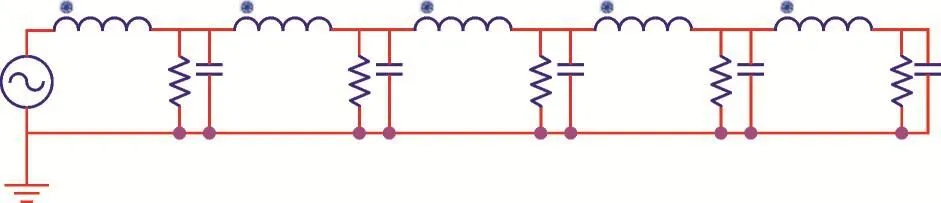
图3 分布参数电路模型Fig.3 Distributed parametric circuit

代入后进行仿真运行，读取电源电位幅值，而冲击接地电阻即为冲击电压幅值与冲击电流幅值的比值。

3 电感仿真结果分析

仿真模型采用直径12 mm的圆钢，水平伸长接地体的长度分别为10 m、20 m、30 m、40 m、50 m，把每段接地体沿长等分成的5个单元，以引流点为起点分为1到5。采用ANSYS软件，进行建模、施加边界条件、端点加载电流后，获得水平伸长接地体静磁场的求解。基于磁场能量法，根据公式（8）计算水平伸长接地体各单元的电感结果，如表1所示。

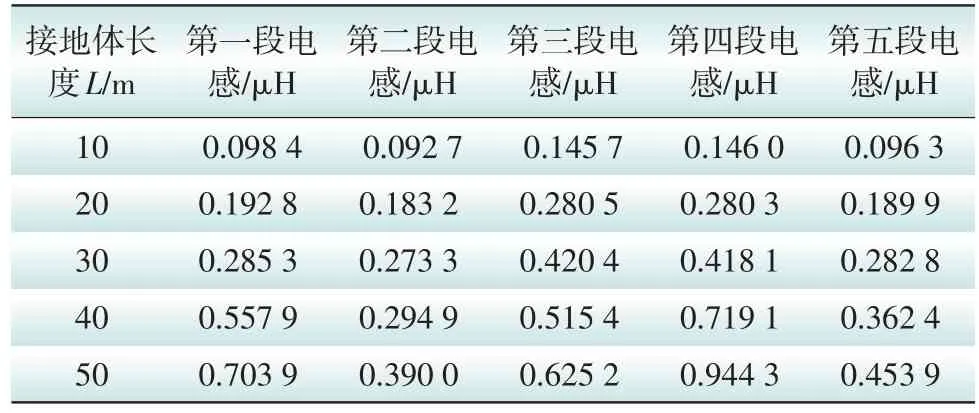
表1 不同接地体长度各段电感值Table 1 Inductance values of different lengths of grounding bodies

由表1数据可知：

1）在相同环境和接地体长度下，水平伸长接地体的各段最高和最低电感值相差1.5～2.4倍。

2）当电流从始端向末端流过时，不同长度接地体的电感都大致呈现先增大后减小的分布规律。而始端接地体由于是引流注入点，所以电感值相比有所提高。

综上所述，接地体各段电感值存在较大差异，而现阶段运用传统经验公式把接地体各段电感计算作常数，则会导致后续得到的冲击接地电阻精度较差。

4 有限元法计算验证

利用分析的电感计算方法，以不同长度的水平接地体和多种土壤电阻率作为变量，进行分布参数电路模型的仿真计算，其中激励电流波形采用幅值20 kA、2.6/50 μs端点引流，埋深均为0.6 m。土壤为均匀模型，电阻率分别取于5～50 Ω·m。为了避免火花效应和电感效应的相互干扰，在计算冲击接地电阻中不考虑火花效应。最后把第3节计算得到的电感值带入分布参数电路模型的仿真计算，比较不同电感计算方式下的冲击电压波形和冲击接地电阻。

20世纪50年代在澳大利亚发现了分散性土，在对冲蚀、管涌破坏的案例调查、分析和研究时，科研人员发现黏性土在有水条件下表现出分散现象，此现象归结为水利工程破坏的原因。此结论随后在各国引起重视，均出现分散性黏土引起工程事故的案例。美国学者从野外调查、室内试验以及补救措施等方面系统性研究了分散性土的分散机理、产生原因以及改进方法，并取得了良好的成果[5-6]，世界上许多国家也对其进行了相关研究。在黑龙江省发现分散性土后，国内学者也进行了深入试验研究[7]。随后在新疆、山东等省的工程建设中也遇到分散性土情况[8-15]，对分散性土筑坝在工程设计和施工中予以高度重视。

4.1 冲击电压波形对比

冲击接地电阻是人为规定为接地极的电位幅值与电流幅值的比值。而采用的冲击电流参数均是幅值20 kA、2.6/50 μs的波形，因此选取了个别变量得到如图4所示冲击电压波形进行比较。

由图4可知：

1）2种计算电感得到的冲击电压波形有较大差异，传统经验法得到的冲击电压峰值要大于有限元法，尤其是在低土壤电阻率和短接地体条件下。

2）两者波形的差异时间普遍在峰值区域，当时间大于4 μs之后，两者波形则开始基本重合。说明接地体各段的电感值主要影响的是冲击电压幅值。

综上所述，冲击电压波形受土壤电阻率和接地体长度影响较大；在低土壤电阻率条件下，2种冲击电压在波峰时间区域内波形有明显不同。而电压幅值的较大区别，就会造成冲击电阻的差异。

4.2 冲击接地电阻差异

为了进一步分析土壤电阻率和伸长接地体长度对冲击接地电阻的影响，着重选取了多个低土壤电阻率及多种伸长接地体长度。分别带入分布参数电路模型的仿真计算冲击接地电阻，得到传统公式结果和考虑互感的有限元法结果，这里将C设为2种冲击接地电阻的比值：

得到以土壤电阻率为横坐标的不同接地体长度下C值走势，如图5所示。

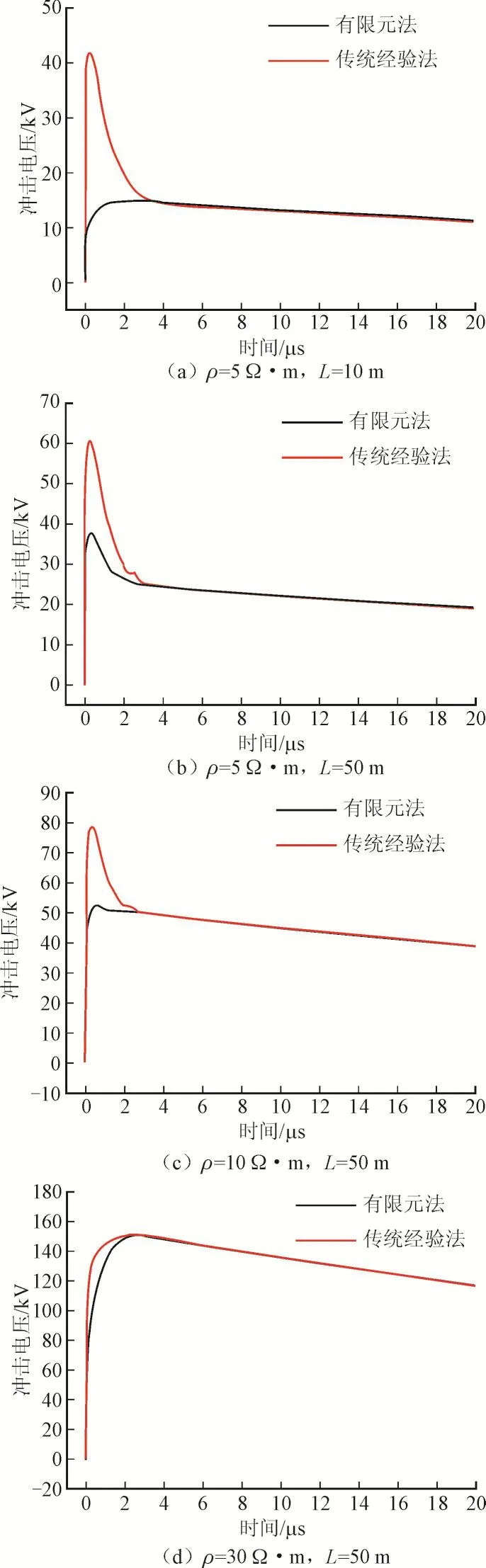
图4 2种电感计算方法在不同参数下冲击电压波形的比较Fig.4 The comparison of the impulse waves under different parameters by two calculation methods of inductance

1）在低土壤电阻率环境下，2种方法得到的冲击接地电阻值有较大不同。同一长度下，当土壤电阻率小于30时，两者差异随土壤电阻率的减小而增大；当土壤电阻率大于30时，两者比值基本为1。

2）在低土壤电阻率环境下，伸长接地体长度越短，传统方法计算冲击接地电阻结果与有限元法的比值也就越大。

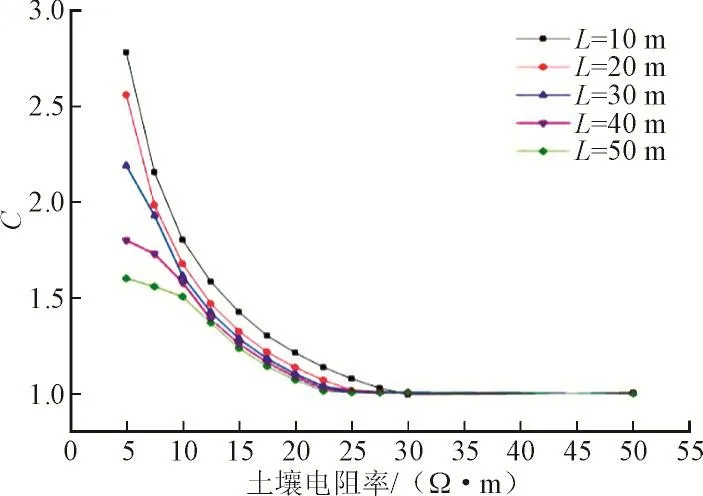
图5 不同接地体长度在不同土壤电阻率下的两种结果比值变化曲线Fig.5 The comparison of two results of different grounding lengths in the soils of different resistivities

综上所述，在低土壤电阻率环境下，土壤电阻率越低，伸长接地体长度越短，利用传统公式计算电感得到的冲击接地电阻值精度也就越差。

5 结论

采用有限元法计算与分析了考虑互感的输电线路杆塔水平伸长接地体冲击接地电阻。计算得到：各段水平接地体电感值之间有较大差异，最高相差2.4倍左右；总体大致呈现两端小、中间大的分布规律。与传统法进行冲击电压波形和冲击接地电阻对比得到：低土壤电阻率条件下，两者的冲击电压幅值差异较大；土壤电阻率越低，伸长接地体长度越短，利用传统公式计算电感得到的冲击接地电阻值精度也就越差。因此考虑了互感的模型所得的数据更加符合实际结果。

本文仅把土壤电阻率和接地体长度作为控制参数，而不同接地体形状和激励电流波前时间对于接地体冲击系数的影响有待进一步研究。

[1]IEEE guide for prot ective grounding of power lines：ANSI/ IEEE Std 1048 TM-2003[S].New York，USA：Institute of Electrical and Electronics Engineers，2003.

[2]鲁志伟，常树生，谭春力.计及铁磁材料饱和特性的地网接地阻抗的计算[J].高电压技术，2009，35（2）：290-293. LU Zhiwei，CHANG Shusheng，TAN Chunli，et al.Calculation of grounding impedance of large substation considering the steel permeability saturation characteristics[J]. High Voltage Engineering，2009，35（2）：290-293.

[3] 张波，何金良，曾嵘.电力系统接地技术现状及展望[J].高电压技术，2015，41（8）：2569-2582. ZHANG Bo，HE Jinliang，ZENG Rong，et al.State of art and prospect of grounding technology in power system[J]. High Voltage Engineering，2015，41（8）：2569-2582.

[4]邓长征.线路杆塔接地装置冲击特性及试验系统的研究[D].武汉：武汉大学，2013.

[5]解广润.电力系统过电压[M].北京：水利电力出版社，1985：58-60.

[6]HE Jinliang，ZENG Rong，TU Youping，et al.Laboratory investigation of impulse characteristics oftransmission tower grounding devices[J].IEEE Transactions on Power Delivery，2003，18（3）：994-1001.

[7]徐华，文习山，黄玲.关于冲击接地电阻测量的探讨[J].高电压技术，2006，32（8）：79-81. XU Hua，WEN Xishan，HUANG Ling，et al.Discussion on the impulse grounding resistance measurement[J].High Voltage Engineering，2006，32（8）：79-81.

[8]何金良，孔维政，张波.考虑火花放电的杆塔冲击接地特性计算方法[J].高电压技术，2010，36（9）：2107-2111. HE Jinliang，KONG Weizheng，ZHANG Bo.Calculating method of impulse characteristics of tower grounding devices considering soilionization[J].High Voltage Engineering，2010，36（9）：2107-2111.

[9] 何金良，曾嵘.电力系统接地技术[M].北京：科学出版社，2007.

[10]曾嵘，何金良，高延庆，等.垂直分层土壤中测试电极布置对变电站接地电阻测量值的影响[J].电网技术，2000，24（10）：36-39. ZENG Rong，HE Jinliang，GAO Yanqing，et al.Influence of arrangement of electrodes on grounding resistance measurement of substation in vertical-layered soil[J].Power System Technology，2000，24（10）：36-39.

[11]卡兰塔罗夫，采伊特林.电感计算手册[M].陈汤铭，等，译.北京：机械工业出版社，1992.

[12]张波，崔翔，赵志斌，等.计及导体互感的复杂接地网的频域分析方法[J].中国电机工程学报，2003，23（4）：77-80，118. ZHANG Bo，CUI Xiang，ZHAO Zhibin，et al.Analysis of the complex groundnig grids in frequency domain conside-ring mutual inductances[J].Proceedings of the CSEE，2003，23（4）：77-80，118.

[13]倪有源，黄亚，林勇.电缆三维磁场分析与自感计算[J].合肥工业大学学报（自然科学版），2012，35（10）：1330-1334，1432. NI Youyuan，HUANG Ya，LIN Yong.3-D magnetic field analysis and self-inductance computation for cable[J].Journal of Hefei University of Technology（Natural Science Edition）2012，35（10）：1330-1334，1432.

[14]解广润.电力系统接地技术[M].北京：中国电力出版社，1989.