光伏发电MPPT失效现象分析

张小莲，郝思鹏，陈凡，翟晶晶，王正齐

（南京工程学院电力工程学院，江苏南京 211167）

随着环境污染与能源紧缺日益严峻，世界各国都在努力寻求低碳策略。我国也提出2020年单位GDP的CO2的排放量比2005年下降40%到50%[1-2]。作为CO2主要来源的电力行业，发展新能源技术是促进行业低碳发展的重要环节。其中，光伏发电由于其无污染、无噪音、可再生等优点受到广泛的关注和青睐[2]。

为了使光伏电池能够跟随光照强度和温度始终保持最大功率输出，光伏发电系统需要采用最大功率点跟踪（maximum power point tracking，MPPT）技术[3-5]。目前常用的MPPT算法主要有固定参数法和自适应搜索法，前者包括恒定电压法和开路电流法，后者主要包括扰动观察法（perturb and observe，P&O）、电导增量法[6-8]以及较复杂的粒子群算法[9-10]、模糊逻辑法[11-12]等。固定参数法根据系统处于最大功率点时电压和电流与系统开路电压或短路电流的近似关系进行控制，其控制精度较低[4]。自适应搜索法中扰动观察法通过人为扰动系统电压或变流环节占空比来确定系统工作点相对于最大功率点的位置，并据此将电压逐步控制到最大功率点对应的电压值；电导增量法原理与此类似：这类算法无需预知系统特性参数，对系统参数以及环境因素具有一定的自适应能力，且实施简便，因此应用较为广泛。

然而，扰动观察法在实际应用中仍存在以下3方面的问题[7，12-13]：1）搜索速度与精度的矛盾；2）最大功率点处的振荡；3）环境因素变化导致搜索方向错误。针对上述问题，现有研究主要从环境因素对算法的影响机理以及变步长设计两方面着手。目前，对于环境因素导致搜索方向出错的机理研究报道较少。文献[14]研究了扰动观察法主要参数的设计，即扰动周期和扰动步长，指出最优的扰动步长应能排除外界环境因素的干扰，但该文献并未具体分析搜索方向出错的机理以及避免出错的参数设计方法。文献[15]研究了搜索方向出错的原因，并通过理论分析给出了避免出错的扰动步长的取值范围，然而该取值范围与光照变化速率、光伏电池系统参数等密切相关，文献仅根据特定的光照变化速率和系统参数设定扰动步长，并未讨论光照变化速率等因素对参数取值以及搜索方向出错的影响。

综上所述，本文基于光伏电池小信号模型的理论分析，得出了环境因素导致扰动观察法搜索方向出错的机理，并通过仿真研究了光照变化速率、变化持续时长对搜索方向出错次数、错误概率、系统能量损失的影响，对于改善复杂环境下光伏发电系统最大功率点跟踪控制效果具有指导意义。

1 光伏发电MPPT控制原理

1.1 光伏电池数学模型与MPPT控制

根据光伏电池等效电路的电压电流关系，光伏电池工程实用输出I-U特性如式（1）所示[16-17]。

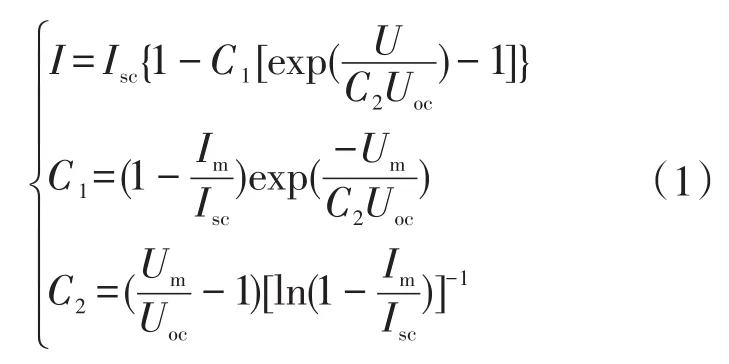
式中：I为光伏电池输出电流；U为光伏电池输出电压；Isc、Uoc、Um和Im分别为标准光照强度和温度下光伏电池的短路电流、开路电压、最大功率点对应的电压和电流。其中，标准光照强度为1 000 W/m2，标准温度为25℃。

当实际光照强度和温度并非标准值时，需要对上述模型中的Isc、Uoc、Um和Im进行修正，如式（2）所示[16]。

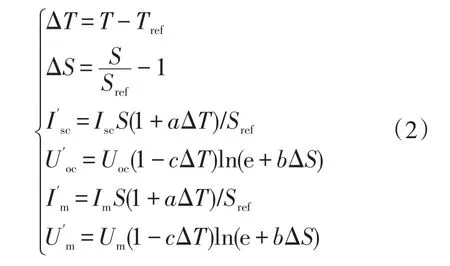
式中：T和S分别为实际温度和光照；Tref和Sref分别为标准温度和光照强度；a、b、c为修正系数；e为自然对数的底。

根据光伏电池输出特性，特定光照和温度下，存在唯一最优电压Uopt，使光伏电池输出功率达到最大值 Pmax，称为最大功率点（maximum power point，MPP）。该最大功率点将随光照和温度而变化。因此，最大功率点跟踪控制通过控制光伏电池输出电压处于Uopt，使其始终保持最大功率输出。实际光伏发电系统一般通过控制变流环节开关器件的占空比来实现MPPT控制[14]。

1.2 扰动观察法的原理

扰动观察法是给定MPPT控制的参考输入的算法，其目的是给出参考电压，引导系统跟踪至最大功率点。该算法基本原理为[4，16]：给定ΔU的扰动后，若光伏电池输出功率变化量ΔP为正，则沿原方向继续扰动U，反之，则反向扰动U，反复进行可使运行点始终向着P增大的方向移动，最终到达MPP，如图1所示。

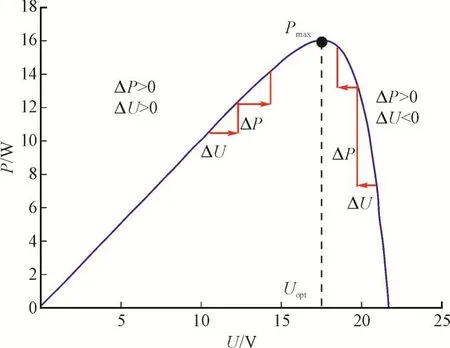
图1 扰动观察法原理图Fig.1 Schematic diagram of the P&O method

扰动观察法根据式（3）确定参考电压U以及扰动步长ΔU：

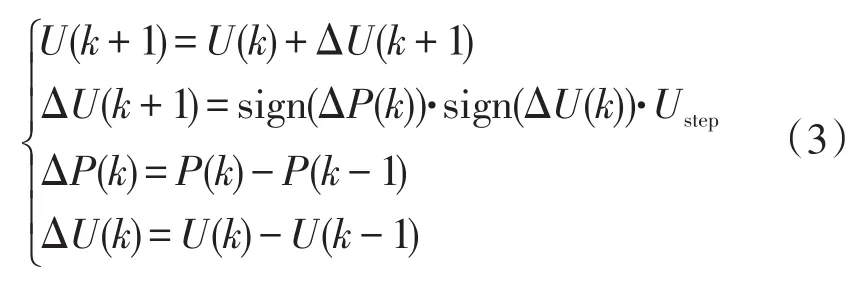
式中：Ustep＞0为电压调整步长；k为迭代次数。

扰动观察法实质上是利用光照和温度恒定时光伏电池P-U曲线的单峰值特性，以及sign（ΔP/ΔU）与系统运行点的关系，即ΔP/ΔU＞0时运行点位于MPP左侧，反之则位于右侧，以此确定系统运行点与MPP的相对位置，最终逐步搜索至MPP。

2 扰动观察法失效现象分析

扰动观察法包含扰动步长、扰动周期和扰动方向（也称为搜索方向）三大要素。其中扰动步长决定该算法搜索至MPP的速率以及电压在MPP附近的振荡幅度；扰动周期决定算法的搜索速率以及电压在MPP附近的振荡频率；搜索方向决定该算法能否正确搜索至MPP。因而，搜索方向是否正确对于算法的有效性至关重要。

本节将通过光伏电池小信号模型和仿真算例分析搜索方向误判而导致的MPPT失效现象及其产生的机理。

2.1 失效现象

图2给出了应用扰动观察法实现MPPT时的失效现象。具体地，光照强度在0.10～0.11 s、0.15～0.17 s期间发生上升和下降变化，此时光伏电池输出电压在搜索MPP时均出现错误的搜索方向（如图2（b）中黑色虚线框所示），致使实际电压U偏离Uopt，从而导致实际功率P与Pmax的差距。

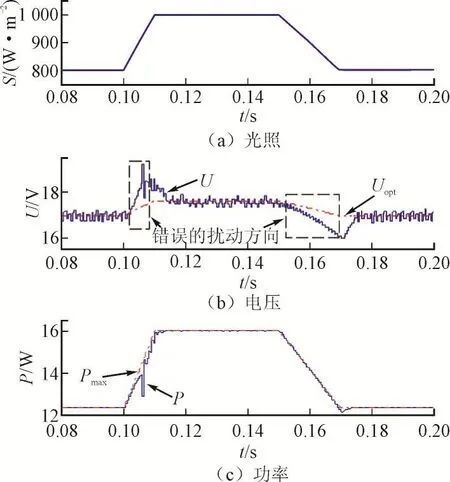
图2 扰动观察法的失效现象Fig.2 The failure of the P&O method

图3和图4分别展示了光照上升（0.10～0.11 s）和下降期间（0.16～0.17 s）电压U与Uopt的差异、扰动观察法的搜索方向Drc与正确搜索方向Drightrc、系统在P-U曲线上的运行轨迹。其中，Drc和Drightrc 定义为：

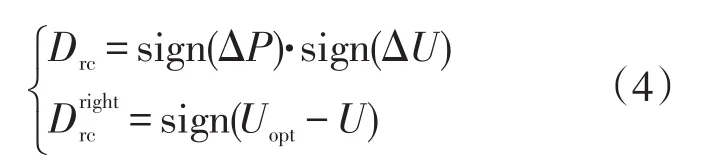
图3 光照强度上升变化时的失效情况（0.10～0.11 s）Fig.3 The failure of the P&O method under rising solarirradiance（during 0.1 to 0.11 s）

由图3（b）可知，Drc大部分时候与不符，而且0.102～0.104 s期间系统的运行轨迹亦偏离实际最大功率点——位于最大功率点右侧，且随时间持续向右移动，而非减小至实际最大功率点处，如图3（c）所示。

与图3所示上升变化时的情况不同，当光照发生下降变化时，电压扰动呈现反复反向，因而其运动轨迹交替性地靠近和远离实际最大功率点，但始终难以运行至实际最大功率点，而是在其左侧振荡，如图4（c）运行轨迹所示。

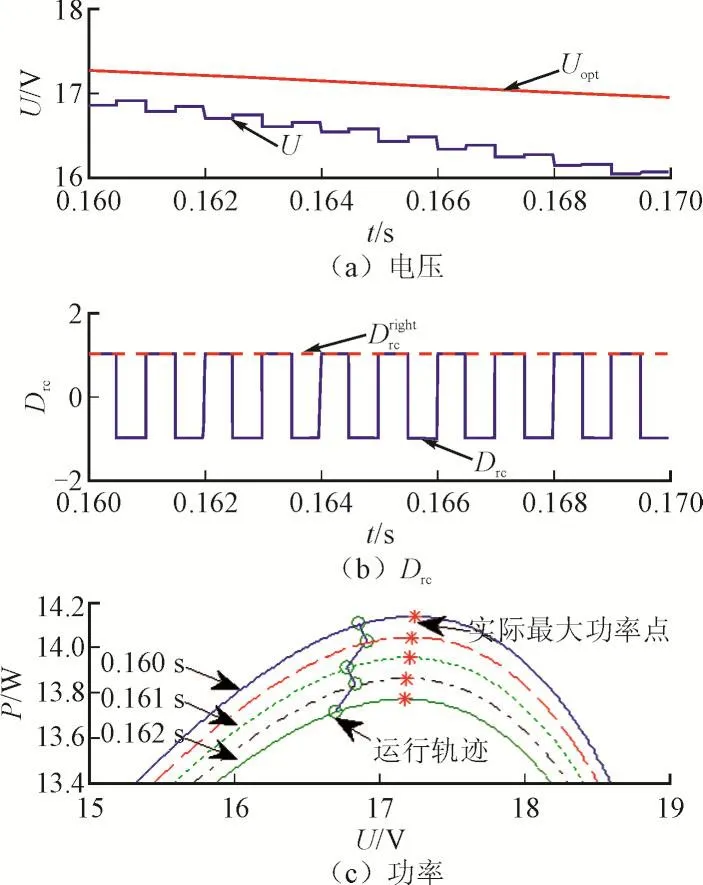
图4 光照强度下降变化时的失效情况（0.16～0.17 s）Fig.4 The failure of the P&O method under decreasingsolar irradiance（during 0.16 to 0.17 s）

2.2 失效现象的机理分析

通过上述分析可知，当光照变化时，系统运行点将在一簇P-U曲线上切换，因此扰动观察法凭借sign(ΔP)·sign(ΔU)确定的搜索方向已不能正确反映运行点相对于最大功率点的位置。本节将基于光伏电池小信号模型对上述失效现象产生的机理进行分析。

2.2.1 机理分析

根据扰动观察法的原理，扰动电压后，输出功率变化量ΔP是确定下一周期搜索方向的关键因素。然而，当光照和温度变化时，光伏电池P-U特性也随之变化，ΔP成为外界环境和人为扰动电压共同作用的结果，如式（5）所示。

式中，ΔPu、ΔPsun、ΔPT分别为电压、光照和温度变化产生的功率变化量，令ΔPair=ΔPsun+ΔPT为环境变化产生的功率变化量。

因而，外界环境变化将对扰动观察法搜索方向的判断产生干扰，包括以下3种情况：

1）ΔPu与ΔPair同号，则搜索方向正确；

2）ΔPu与ΔPair异号且，则ΔPu占主导地位，搜索方向正确；

3）ΔPu与 ΔPair异号且，则 ΔPair占主导地位，搜索方向错误。

综上，当出现式（6）所示条件时，算法将出现错误的搜索方向。

2.2.2 机理分析的仿真验证

为验证上述机理分析，首先通过光伏电池小信号模型对环境因素和电压扰动产生的功率增量进行解耦，即计算获得光伏电池输出功率P对电压、光照和温度的偏导数，然后对2.1节图2所示的算例进行分析。值得注意的是，为简化分析，本文仅讨论光照变化的情况，温度变化对算法的影响与此类似。

根据式（1）和式（2），光伏电池输出功率P对电压U和光照强度S的偏导数如式（7）和式（8）所示。

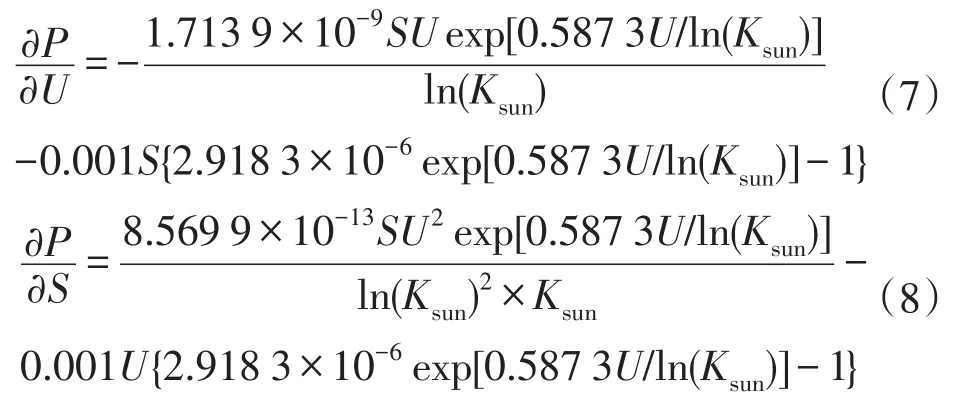
式中，Ksun=0.000 5S+2.218 3。

那么系统运行过程中，可按式（9）解耦ΔP。

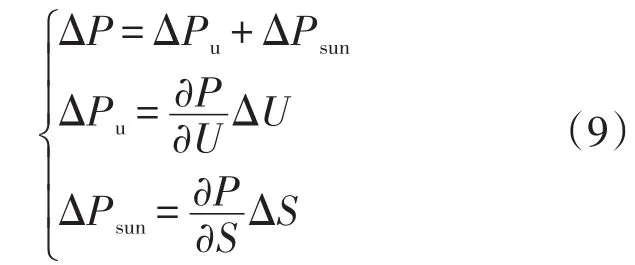
那么，计算获得图2中光照上升变化和下降变化期间的flag、ΔPu、ΔPsun和ΔP，如图5和图6所示。其中，flag为搜索方向正确与否的标识，其定义如式（10）所示，搜索方向正确时flag=1，反之flag=-1。

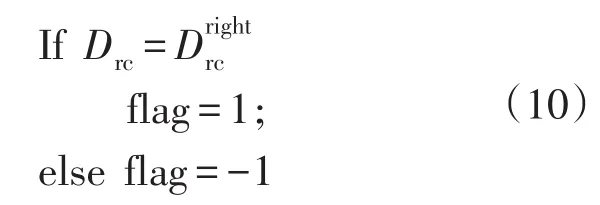
此外，为更好地展示ΔPu、ΔPsun对flag的影响，图5（c）和图6（c）仅给出ΔPu、ΔPsun异号时的ΔP，其中红色柱形图为ΔPu占主导时的ΔP，蓝色柱形图为ΔPsun占主导时的ΔP。

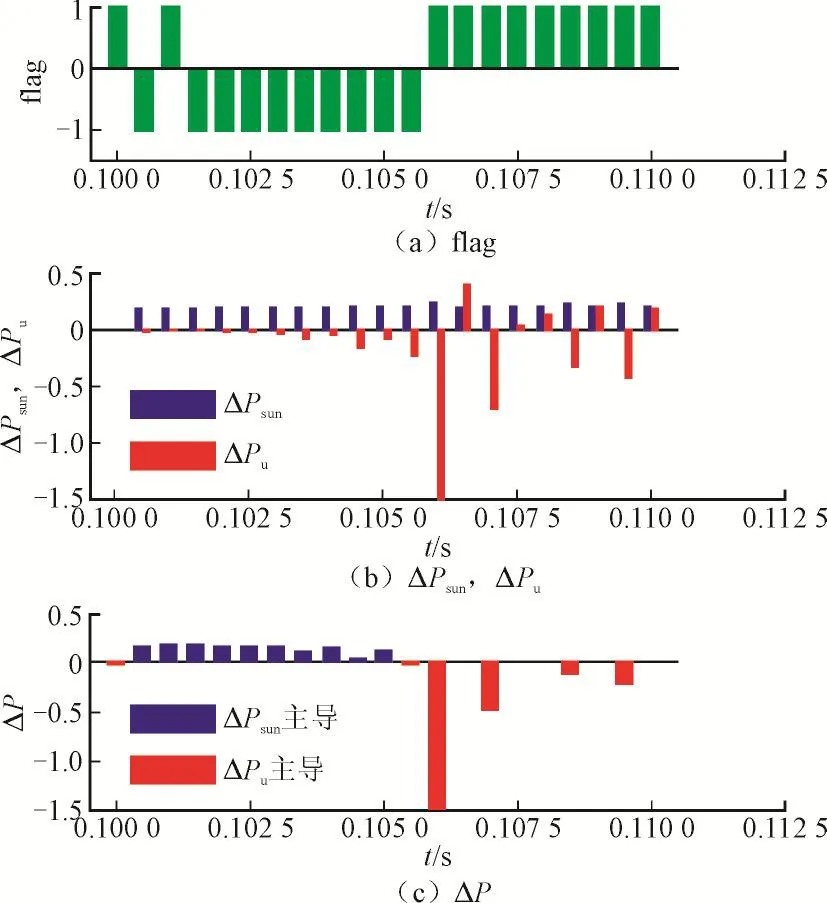
图5 光照强度上升时的ΔP与搜索方向（0.10～0.11 s）Fig.5 ΔP and searching direction under rising solar irradiance（during 0.1 to 0.11 s）

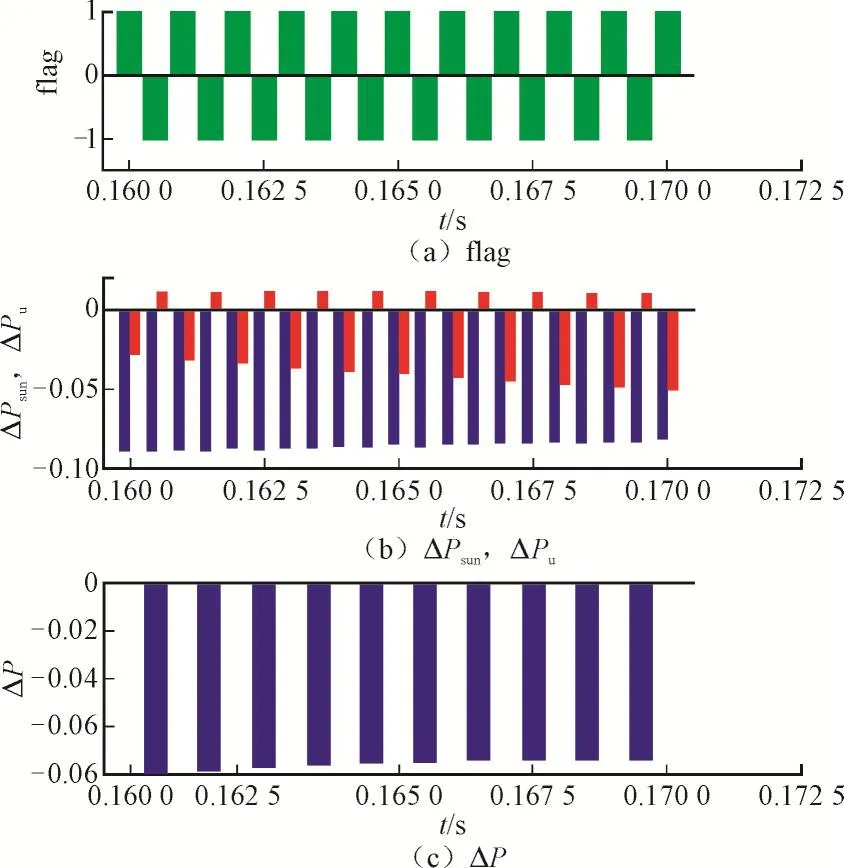
图6 光照强度下降时的ΔP与搜索方向（0.16～0.17 s）（图中标识同图5）Fig.6 ΔP and searching direction under decreasing solar irradiance（during 0.16 to 0.17 s）（with the same legend to Fig.5）

由图5（a）、图5（c）和图6（a）、图6（c）可知，当ΔPu、ΔPsun异号且ΔPsun占主导时flag显示搜索方向判断错误，而ΔPu、ΔPsun异号且ΔPu占主导时flag判断正确，ΔPu、ΔPsun同号时也能获得正确的搜索方向，验证了上述机理分析的正确性。

3 失效现象的概率与能量损失

本节将通过算例研究扰动观察法失效现象发生的概率、能量损失与光照强度变化速率、变化持续时长之间的关系。

3.1 仿真模型与算例设计

3.1.1 仿真模型及其参数

本文参考文献[7]建立图7所示光伏发电仿真系统，由光伏电池、Boost电路、输出滤波电容、负载电阻、MPPT算法模块以及PWM驱动电路构成，具体参数如表1所示。扰动观察法参数设置为：占空比扰动步长Δd=0.01，扰动周期Tpo=0.001 s。

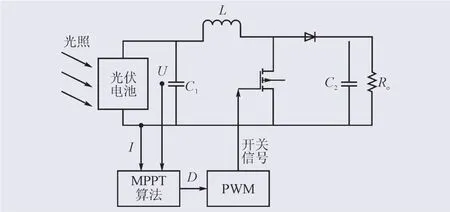
图7 光伏发电系统模型Fig.7 Simulation model of the PV generation system

表1 光伏发电系统参数Tab.1 Parameters of the PV generation system

3.1.2 算例设计

本文采用光照强度上升斜坡和下降斜坡变化来分析光照与失效现象概率、能量损失的关系，且单个算例仅包含上升斜坡变化或下降斜坡变化。根据光照变化速率以及持续时长不同，构造20组仿真算例，其中光照变化速率、持续时长、光照变化的初始时刻、初始光照值等参数可参见后续仿真结果。

3.2 光照变化与失效概率、能量损失的关系

3.2.1 不同光照变化速率下的失效情况

针对具有不同变化速率ks的光照强度应用扰动观察法，计算获得光照变化期间搜索方向错误次数ne、错误概率perr以及能量损失率η，如表2所示。表2所述算例的光照强度变化初始时刻均为0.2 s，持续时长TL为0.01 s，上升变化的初始值为800 W/m2，下降变化的初始值为1 000 W/m2，仿真总时长为0.3 s。

错误概率perr以及能量损失率η定义如式（11）和式（12）所示。

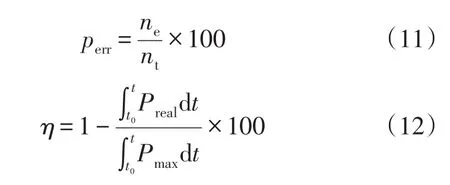
式中：nt为光照变化期间算法迭代总次数；t0为光照变化初始时刻；t为结束时刻；Preal为光伏电池输出实际功率；Pmax为对应最大功率。

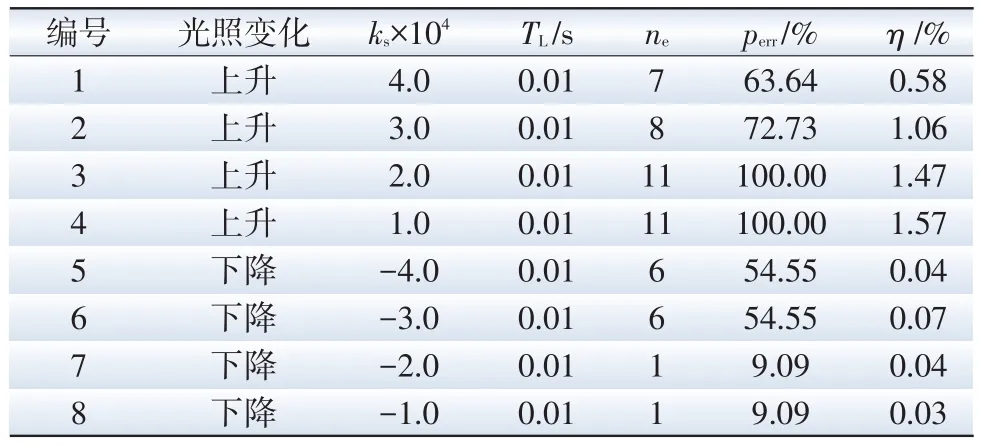
表2 不同光照变化速率下的失效概率和能量损失Tab.2 Failure probability and energy loss under different changing rates of solar irradiance

3.2.2 光照变化持续时长与失效现象的关系

同理可计算获得不同持续时长的光照变化对应的搜索方向错误次数ne、错误概率perr以及能量损失率η，如表3所示。表3所述算例的光照强度变化初始时刻均为0.2 s，上升变化的初始值为800 W/m2，下降变化的初始值为1 000 W/m2，仿真总时长为0.3 s。

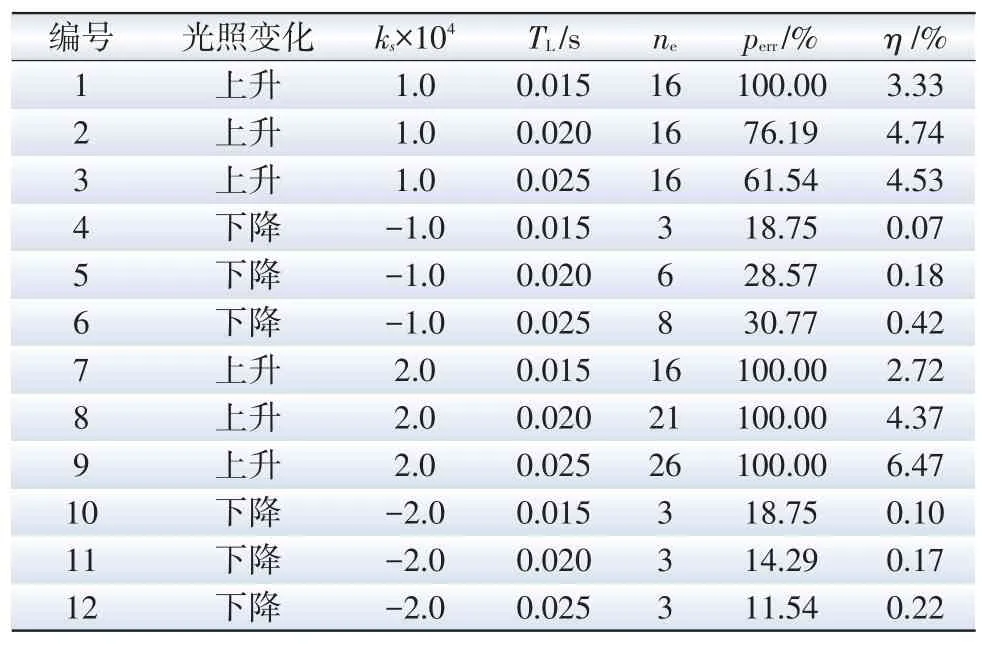
表3 不同持续时长下的失效概率和能量损失Tab.3 Failure probability and energy loss under different changing durations of solar irradiance

图8和图9分别给出了上述算例中光照上升变化和下降变化时的输出特性。其中图8为表3中算例9的电压U、输出功率P、占空比d和功率变化量ΔP，图9为表3中算例6的输出特性。

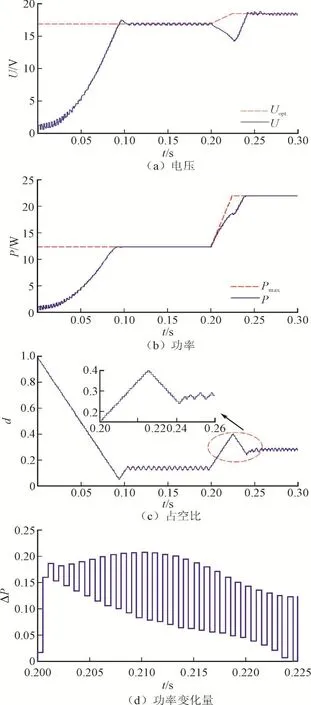
图8 表3中算例9的输出特性Fig.8 The outputs of Example 9 in Tab.3

3.2.3 仿真结果分析与总结

1）由表2可知，光照变化速率对搜索方向错误次数和能量损失的影响具有随机性；

2）表3表明，光照变化持续时间越长，搜索方向错误次数越多，能量损失则越大。其原因在于光照对搜索方向的干扰时间越长，出错的几率越大；

3）上升变化比下降变化导致的搜索方向错误次数更多，能量损失更大。因为上升变化导致的ΔP多为正值（如图8（d）所示），一旦出现错误的搜索方向，这个错误的方向更容易持续（如图8（c）局部放大所示）。而下降变化导致的ΔP为负值（如图9（d）所示），电压的扰动方向将会反复反向（如图9（c）局部放大所示），因此对于相同的时长，错误的搜索方典型仿真结果如表4所示。向相对于上升变化更少。

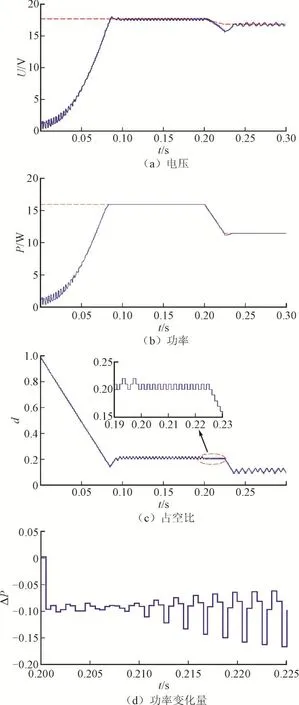
图9 表3中算例6的输出特性（图中标识同图8）Fig.9 The outputs of Example 6 in Tab.3（with the same legend to Fig.8）

表4 典型仿真结果Tab.4 Typical simulation results

4 结语

本文以最大功率点跟踪控制算法中的扰动观察法为研究对象，从理论角度分析了环境因素导致搜索方向出错的机理，并研究了光照强度变化的速率、持续时长对搜索方向出错次数、错误概率、能量损失的影响。

基于光伏电池小信号模型的理论分析表明，环境因素变化导致的光伏电池输出功率增量与人为扰动电压带来的功率增量相反且前者占主导地位，是扰动观察法出现搜索方向错误的根本原因所在，亦表明扰动观察法本身并不具备甄别2种功率增量的机制。这一结论对于改进扰动观察法具有良好的指导意义。此外，本文仿真结果表明，光照强度变化持续时间越长，则扰动观察法搜索方向错误次数越多，能量损失越大，且光照强度持续上升比持续下降导致的搜索方向错误次数更多，能量损失更大。经统计，这种失效现象导致的最大能量损失可达6.47%，搜索方向最大错误概率可达100%。对于规模日益增大的光伏电站，这一损失不可小觑。

[1] 丁然，康重庆，周天睿，等.低碳电网的技术途径分析与展望[J].电网技术，2011，35（10）：1-8. DING Ran，KANG Chongqing，ZHOU Tianrui，et al. Analysis and prospect on technical approaches for low carbon power grid[J].Power System Technology，2011，35（10）：1-8.

[2]艾欣，韩晓男，孙英云.大型光伏电站并网特性及其低碳运行与控制技术[J].电网技术，2013，37（1）：15-23. AI Xin，HAN Xiaonan，SUN Yingyun.Grid-connection characteristics of large-scale photovoltaic power station and its low-carbon operation and control technology[J]. Power System Technology，2013，37（1）：15-23.

[3] 游国栋，李继生，侯勇，等.部分遮蔽光伏发电系统的建模及MPPT控制[J].电网技术，2013，37（11）：3037-3045. YOU Guodong，LI Jisheng，HOU Yong，et al.Analytical modeling and maximum power point tracking control of partially shaded photovoltaic generation system[J].Power System Technology，2013，37（11）：3037-3045.

[4]张超，何湘宁.短路电流结合扰动观察法在光伏发电最大功率点跟踪控制中的应用[J].中国电机工程学报，2006，26（20）：98-102. ZHANG Chao，HE Xiangning.Short-current combined with perturbation and observation maximum-power-point tracking method for photovoltaic power systems[J]. Proceedings of the CSEE，2006，26（20）：98-102.

[5]DALLAGO E，LIBERALE A，MIOTTI D，et al.Direct MPPT algorithm for PV sources with only voltage measurements[J].IEEE Transactions on Power Electronics，2015，30（12）：6742-6750.

[6]KJAER S B.Evaluation of the“hill climbing”and the“incremental conductance”maximum power point trackers for photovoltaic power systems[J].IEEE Transactions on Energy Conversion，2012，27（4）：922-929.

[7] 周东宝，陈渊睿.基于改进型变步长电导增量法的最大功率点跟踪策略[J].电网技术，2015，39（6）：1491-1498. ZHOU Dongbao，CHEN Yuanrui.Maximum power point tracking strategy based on modified variable step-size incrementalconductance algorithm[J].Power System Technology，2015，39（6）：1491-1498.

[8] 杨勇，朱彬彬，赵方平，等.一种电流预测控制的自适应变步长最大功率跟踪方法[J].中国电机工程学报，2014，34（6）：855-862. YANG Yong，ZHU Binbin，ZHAO Fangping，et al.An adaptive and variable step MPPT method based on current predictive controllers[J].Proceedings of the CSEE，2014，34（6）：855-862.

[9]LIAN K L，JHANG J H，TIAN I S.A maximum power point tracking method based on perturb-and-observe combined with particle swarm optimization[J].IEEE Journal of Photovoltaics，2014，4（2）：626-633.

[10]祝青，张兴，李善寿，等.一种基于功率闭环的动态多峰值最大功率点跟踪算法研究与测试[J].中国电机工程学报，2016，36（5）：1218-1227. ZHU Qing，ZHANG Xing，LI Shanshou，et al.Researches and tests of a dynamic multi-peak maximum power point tracking algorithm based on power loop[J].Proceedings of the CSEE，2016，36（5）：1218-1227.

[11]CHIKH A，CHANDRA A.An optimal maximum power point tracking algorithm for PV systems with climatic parameters estimation[J]. IEEE Transactions on Sustainable Energy，2015，6（2）：644-652.

[12]吴海涛，孙以泽，孟婥.粒子群优化模糊控制器在光伏发电系统最大功率跟踪中的应用[J].中国电机工程学报，2011，31（6）：52-57. WU Haitao，SUN Yize，MENG Chuo.Application of fuzzy controller with particle swarm optimization algorithm to maximum power point tracking of photovoltaic generation system[J].Proceedings of the CSEE，2011，31（6）：52-57.

[13]PAZ F，ORDONEZ M.High-performance solar MPPT using switching ripple identification based on a lock-in amplifier[J].IEEE Transactions on Industrial Electronics，2016，63（6）：3595-3604.

[14]ELGENDY M A，ZAHAWI B，ATKINSON D J.Assessment of perturb and observe MPPT algorithm implementation techniques for PV pumping applications[J].IEEE Transactions on Sustainable Energy，2012，3（1）：21-33.

[15]FEMIA N，PETRONE G，SPAGNUOLO G，VITELLI M. Optimization of perturb and observe maximum power point tracking method[J]. IEEE Transactions on Power Electronics，2005，20（4）：963-973.

[16]焦阳，宋强，刘文华.光伏电池实用仿真模型及光伏发电系统仿真[J].电网技术，2010，34（11）：198-202. JIAO Yang，SONG Qiang，LIU Wenhua.Practical simulation model of photovoltaic cells in photovoltaic generation system and simulation[J].Power System Technology，2010，34（11）：198-202.

[17]刘东冉，陈树勇，马敏，等.光伏发电系统模型综述[J].电网技术，2011，35（8）：47-52. LIU Dongran，CHEN Shuyong，MA Min，et al.A review on models for photovoltaic generation system[J].Power System Technology，2011，35（8）：47-52.