具有 Mate-Finding Allee 效应的时滞捕食-食饵系统的稳定性与分支分析

吴瑞雯, 刘秀湘

(华南师范大学数学科学学院, 广州 510631)

具有 Mate-Finding Allee 效应的时滞捕食-食饵系统的稳定性与分支分析

吴瑞雯, 刘秀湘*

(华南师范大学数学科学学院, 广州 510631)

讨论了具有比率依赖功能性反应和食饵受到Mate-Finding Allee效应制约的时滞捕食-食饵系统的稳定性和分支分析. 以时滞量为分支参数,证明当时滞量穿过一些临界值时,系统会在正平衡点处经历Hopf分支,并给出相关的数值模拟结果;给出当系统经历Bogdanov-Takens分支时，时滞量需要满足的限制条件,进而表明时滞对系统有很重要的影响.

Allee效应; Hopf分支; Bogdanov-Takens分支; 捕食-食饵系统; 时滞

美国生态学家Allee通过实验发现,当适度的拥挤时,种群的合适度与种群密度之间存在正相关关系[1],后被称之为Allee效应[2]. 学者们对Allee效应做了大量的研究[3-7]. 最近，文献[8]考虑了食饵受到Mate-Finding Allee效应制约的比率依赖的捕食-食饵系统:

(1)

其中,u和v分别表示食饵和捕食者在t时刻的种群密度,g>1,α>0,α1>0,β>0,δ>0表示Mate-Finding Allee效应的强度.

在实际的种群相互作用时,往往存在时滞[9]. 对于捕食系统而言,由于捕食者存在妊娠期,在捕掠食饵后的繁殖不是瞬时的,因此需要考虑捕食者的妊娠期所引起的时滞,仿照文献[10]、[11]的模型推导方式,考虑以下具有Mate-Finding Allee效应的离散时滞的比率依赖的捕食-食饵系统:

(2)

1 时滞对共存平衡点稳定性的影响

系统(2)存在成对出现的正平衡点E1(u1,v1)和E2(u2,v2),其中

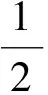
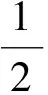
及vi=[(α1-β)/β]ui(i=1,2)当且仅当以下条件成立:

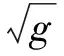
由于时滞不会改变平衡点的个数,而且文献[8]证明了系统(1)会在共存平衡点E2(u2,v2)处经历Hopf分支,故在接下来的讨论仍然关注E2(u2,v2)的动力学性质. 本节主要研究随着时滞的变化,共存平衡点E2(u2,v2)的稳定性的变化情况.

作变换z1=u-u2,z2=v-v2,把E2(u2,v2)平移到原点(0,0),并进行Taylor展开,则系统(2)可改写成

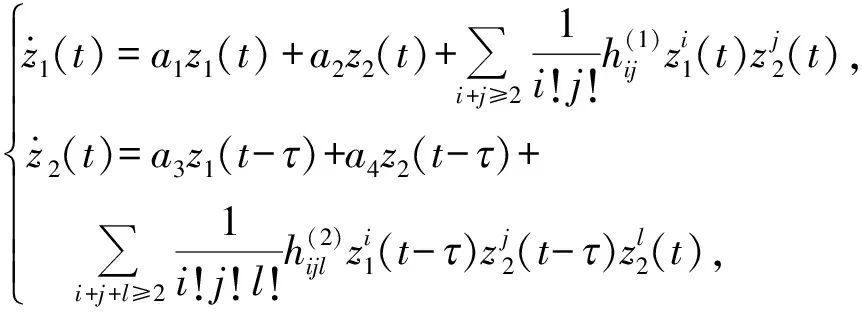
(3)

其中

系统(3)在平衡点(0,0)处的线性化方程为:

(4)

而系统(4)所对应的特征方程为:

(5)

其中A=-a1,B=-a4,C=a1a4-a2a3.

特别地,对于系统(2)的参数g、δ、α、α1、β,提出下面的条件:

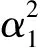
引理1设条件(H1)、(H2)成立，则当

(6)

时，方程(5)有一对纯虚根 ±iω0,其中

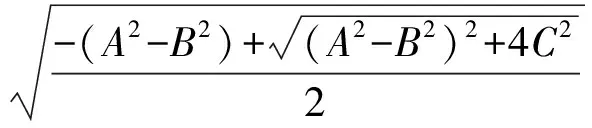
进一步地，有

证明很明显，=0不是方程(5)的根. 假设±iω(ω>0)是方程(5)的根，即对某个≥0,ω满足(iω)2+Aiω+Biωe+Ce=0,分离实部虚部,则

进一步地，得到

ω4+(A2-B2)ω2-C2=0.

(7)

由于 4C2>0,故方程(7)存在唯一的正根

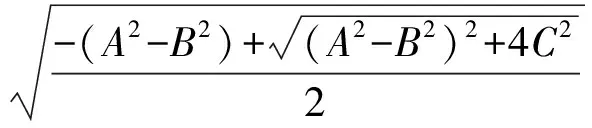
由此亦可计算出

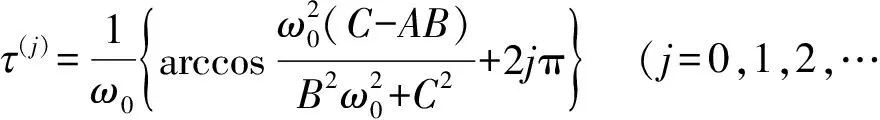
2+(A+B)+C=0,

(8)

并由此可得到

=,

通过计算可知C>0;并结合条件(H2),进一步可知

-(A+B)=a1+a4=

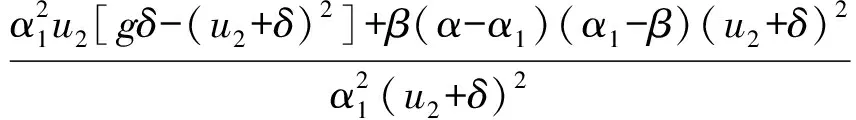
即方程(8)所有的根都具有负实部. 运用文献[14]的结果，则引理1结论得证.

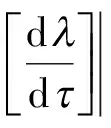
证明方程(5)两边关于求导,得

从而

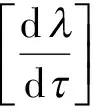
由于

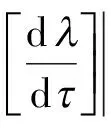
故通过直接计算容易发现

证毕.

结合文献[14]、引理1和引理2，可以得到下面的引理.

引理3设条件(H1)、(H2)成立,关于系统(2)正平衡点E2(u2,v2)的稳定性有以下结论:

综合上述的讨论,可以得到

定理1设条件(H1)、(H2)成立. 对某个j{0,1,2,…},记()=r()±iω()为方程(5)的根,当其满足

r((j))=0,ω((j))=ω0,r′((j))=Re>0,

2 Hopf分支的方向和稳定性

定理1给出了系统(2)在共存平衡点E2(u2,v2)处经历Hopf分支的充分条件. 假设此条件成立,本节利用规范型方法[12-13],进一步分析Hopf分支的方向和分支周期解的稳定性. 通过采用尺度变换t→t/,系统(2)转化为

(9)

则系统(3)等价于

(10)

z′(t)=L()(zt)+F(zt,),

(11)

其中

L()(φ)=

F(φ,)=

这里φ=(φ1,φ2)T([-1,0],2) .

对于某一固定的j{0,1,2,…},由上一节的讨论可知系统(2)在=(j)处经历Hopf分支,令=-(j),则=0是系统(2)的分支点. 为方便起见,仍把记为,则系统(11)改写成:

z′(t)=L((j))(zt)+F0(zt,),

(12)

其中F0(φ,)=L()(φ)+F(φ,(j)+).L(x)是([-1,0],2)到2的连续线性泛函,根据Riesz表示定理可知,存在一个有界变差矩阵η(θ,x)(-1≤θ≤0),使得

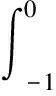
为此，不妨选取

其中θ≠0时δ(θ)=0，θ=0时δ(θ)=1. 根据泛函微分方程的形式伴随理论[15]，可以得到系统(12)在临界分支值(j)处三阶截断规范型的具体形式：

(13)

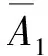
A1=iω0μTν,

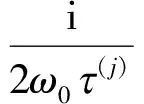
其中

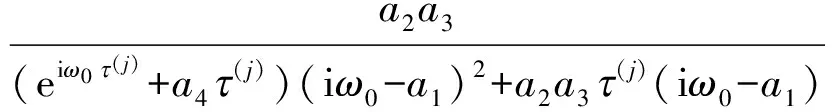
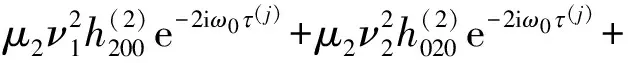
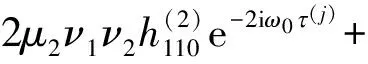
此外，c3的表达式为

c3=μT(j)×

进一步地，有

以及

e2iω0(j)θc2,

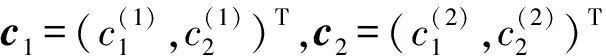
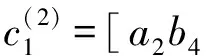
[(2iω0(j)-a4(j)e-2iω0(j))(2iω0(j)-a1(j))-

a2a32(j)e-2iω0(j)],

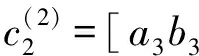
[(2iω0(j)-a4(j)e-2iω0(j))(2iω0(j)-a1(j))-

a2a32(j)e-2iω0(j)],

接下来采用坐标变换x1=w1-iw2,x2=w1+iw2,先转换成实坐标w1、w2,再转换成极坐标w1=ρcosθ,w2=ρsinθ,则规范型(13)变为

(14)

其中,k1=ReA1,k2=ReA3. 因此，根据文献[16],可得以下结果:

定理2设条件(H1)、(H2)成立，系统(10)在=(j)时中心流形上的规范型为系统(14). 进一步地,有

(1)若k1k2<0 (k1k2>0),则在=(j)处系统所经历的Hopf分支是向前的(向后的);

(2)若k2<0 (k2>0),则非平凡周期解是稳定的(不稳定的).

3 Hopf分支的数值模拟

进一步的计算表明ω0=0.081 6,从而(0)=0.087 6,故根据定理1,当=0.05(0,0.087 6)时,平衡点E2是渐近稳定的(图1A);当=1.5>0.087 6时,平衡点E2是不稳定的(图1B);当≈0.087 6时,系统(2)在E2附近经历了Hopf分支. 根据定理2的讨论,Hopf分支性质的重要参数值如下:

a20≈0.617 5+1.609 4i,a11≈-0.407 6+1.372 1i,

a02≈-0.772 8+2.395 8i,a21≈3.777 3+8.543 6i,

c3≈-36.591 7+65.494 1i,

A1≈0.088 0+0.081 3i,A3≈-17.499 0-12.468 4i,

进而有

k1=ReA1≈0.088 0>0,k2=ReA3≈-17.499 0<0,

故系统(2)在E2=(0.158 6,0.052 9)经历了向前的Hopf分支,而且在局部中心流形上所产生的Hopf分支解是渐进稳定的(图1C、D).

4 Bogdanov-Takens 分支的存在性

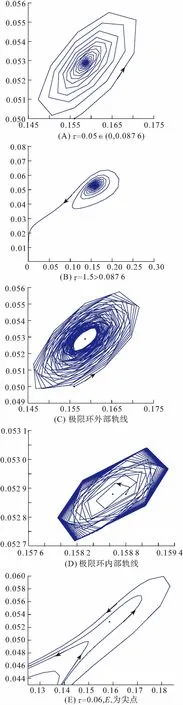
图1 系统(2)轨线分布图

注：图(A)～(D)的系统参数取值为:g=1.44,δ=0.009 5,α=0.8,α1=0.4,β=0.3;图(E)的系统参数取值为:g=1.44,δ=0.022 9,α=0.4,α1=0.4,β=0.3.

为方便描述,考虑如下系统:

(15)

其中有下面条件成立

(H3)

(16)

进一步通过变换z1=u-u*,z2=v-v*,把E*(u*,v*)平移到原点并进行Taylor展开,从而得到以下系统:

(17)

其中

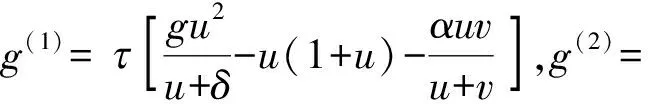
z′(t)=L(zt)+F(zt),

(18)

其中L:→2,F:→2的表达式如下:

L(φ)=

F(φ)=

这里φ=(φ1,φ2)T([-1,0],2) .

系统(18)在原点处的线性化方程为z′(t)=L(zt),则相应的特征方程为

2+(e-1)=0.

很明显, 如果条件

(H4)

=

由泛函微分方程的形式伴随理论[15]可知，系统(18)在局部中心流形上的规范型可以写为

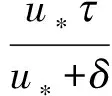
定理3假设条件(H3)、(H4)成立，若

≠(2±)·,

则k1≠0,k2≠0,即意味着唯一的正平衡点E*(同时亦为Bogdanov-Takens奇点)仍为时滞系统(16)的余维-2的尖点,系统会在E*经历Bogdanov-Takens分支(图1E).

5 小结

本文讨论了具有 Mate-Finding Allee 效应和比率依赖功能性反应的时滞捕食-食饵系统的稳定性和分支现象. 通过分析时滞量对共存平衡点E2稳定性的影响,得到Hopf分支的存在性. 类似常微分系统(1),泛函微分系统(2)也会在E*附近经历Bogdanov-Takens分支,但此时对时滞有额外的条件限制. 有关Bogdanov-Takens分支现象所出现的鞍结分支曲线(SN),Hopf分支曲线(H)和同宿曲线(HL)可作进一步的探究与讨论.

[1] ALLEE W C. Animal aggregations,a study in general sociology [M]. Chicago:University of Chicago Press,1931.

[2] ALLEE W C. The social life of animals[M]. London:William Heinemann,1938.

[3] STEPHENS P A,SUTHERLAND W J,FRECKLETON R. What is the Allee effect[J]. Oikos,1999,87:12-27.

[6] CUI R,SHI J,WU B. Strong Allee effect in a diffusive predator-prey system with a protection zone[J]. Journal of Differential Equations,2014,256:108-129.

[7] KIM C,SHI J. Existence and multiplicity of positve solutions to a quasilinear elliptic equation with strong Allee effect growth rate[J]. Results in Mathematics,2013,64:165-173.

[8] WU R W,LIU X X. Dynamics of a predator-prey system with a mate-finding Alleeeffect[J]. Abstract Applied Analysis,2014(2014):Art 673424,14 pp.

[9] 吴敏,翁佩萱. 具有阶段结构的多时滞SIR扩散模型的稳定性[J]. 华南师范大学学报(自然科学版),2013,45(2):20-23.

WU M,WENG P X. Stability of a stage-structured diffusive SIR model with delays[J]. Journal of South China Normal University(Natural Science Edition),2013,45(2):20-23.

[10] BUSH A W,COOK A E. The effect of time delay and growth rate inhibition in the bacterial treatment of wastewater[J]. Journal of Theoretical Biology,1976,63:385-395.

[11] XIAO D,RUAN S. Multiple bifurcations in a delayed pre-dator-prey system with nonmonotonic functional response[J]. Journal of Differential Equations,2001,176:494-510.

[12] FARIA T,MAGALHES L T. Normal forms for retarded functional differential equations and applications to Bogdanov-Takens singularity[J]. Journal of Differential Equations,1995,122:201-224.

[13] FARIA T,MAGALHES L T. Normal forms for retarded functional differential equations with parameters and applications to Hopf bifurcation[J]. Journal of Differential Equations,1995,122:181-200.

[14] COOKE K L,GROSSMAN Z. Discrete delay,distributed delay and stability switches[J]. Journal of Mathematical Analysis and Applications,1982,86:592-627.

[15] HALE J K. Theory of functional differential equations[M]. New York:Springer,1977.

[16] CHOW S N,HALE J K. Method of bifurcation theory[M]. New York:Springer,1982.

Stability and Bifurcation Analysis in a Delayed Predator-Prey Systemwith Mate-Finding Allee Effect

WU Ruiwen, LIU Xiuxiang*

(School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China)

The stability and bifurcation analysis of a delayed ratio-dependent predator-prey system with a Mate-Finding Allee effect on prey is discussed. The delay is chosen as the bifurcation parameter and the system may have experience Hopf bifurcation. Moreover, the results show that under some conditions the system has a Bogdanov-Takens singularity, which indicates that the delay has an important effect on the dynamical behaviors of the system.

Allee effect; Hopf bifurcation; Bogdanov-Takens bifurcation; predator-prey system; time delay

2016-08-08 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

广东省自然科学基金项目(S2012010010034，2016A030313426)

*通讯作者:刘秀湘,教授,Email:liuxx@scnu.edu.cn.

O175.13

A

1000-5463(2017)06-0101-06

【中文责编：庄晓琼 英文审校：叶颀】