洪水形成过程的协同性探究

汪丽娜, 陈晓宏

(1. 华南师范大学地理科学学院， 广州 510631； 2. 中山大学水资源与环境研究中心， 广州 510275；3. 华南地区水循环和水安全广东普通高校重点实验室 (中山大学)， 广州 510275)

洪水形成过程的协同性探究

汪丽娜1*, 陈晓宏2,3

(1. 华南师范大学地理科学学院， 广州 510631； 2. 中山大学水资源与环境研究中心， 广州 510275；3. 华南地区水循环和水安全广东普通高校重点实验室 (中山大学)， 广州 510275)

以武江流域犁市站历史上的53场洪水为例，选取17个时段洪量作为序参量，建立洪水过程协同性评价模型，分析洪水过程的协同性是否发生改变. 研究结果表明：尽管武江流域过去发生过较大的洪水，但是从洪水的协同性角度来看，4场大洪水(1968、1994、2002、2006年)形成过程未发生变异，总体上武江流域各场洪水的消退子系统与涨水子系统的相干性不强，表现为洪水形成过程的协同性较差，而在1963年和1991年洪水形成过程的协同性发生了较为明显的变异.

洪水涨水子系统； 洪水消退子系统； 洪水系统； 协同性； 序参量

近年来，随着洪水事件的频繁发生，研究洪水的变异性引起学者们的重视，如：采用RVA(Range of Variability Approach)方法对美国Utah州Colorado河下游2条主要河流筑坝导致的水文变异进行了评价，得到大坝建成前后最小30天流量的变异图[1]；采用基于水文特征的累积序列差值方法，对洪水时间序列进行变异性识别[2]；结合水位变化趋势重新计算洪水频率，表明Mississippi的St.Louis站1993年洪峰重现期发生显著异变[3]；采用珠江三角洲网河区数十年来的人类活动和水文特征资料，发现河道人工采砂以及大洪水冲刷作用导致河床下切，部分断面水位-流量关系变异[4]；基于区间化变量理论，研究了珠江三角洲网河区的水位空间变异性[5]；将水文序列变点分析的灰关联法应用于珠江三角洲顺德河网区的水位变化分析[6]；评价东江中上游流域(1952—2002年)水文变异情况，得出东江中上游流域年最小3 d流量变异最大而年最小90 d流量变异最低的结论[7]. 总体上，对于洪水异变这一领域的研究，主要是解析洪水某一要素的异变. 事实上，洪水过程包含着洪水的涨水子系统和消退子系统，这2个子系统共同构成洪水过程整体，而构成的过程就体现出协同性. 从洪水形成过程的协同性角度分析洪水的异变，可以更准确地调控洪水的演变过程，把握洪水的涨水、消退子系统的相干性，使洪水的利用更合理. 然而，目前关于洪水形成过程协同性的探究较少.

关于协同的研究涉及多个领域，例如：耕地资源与城市化进行之间、环境状况与经济发展之间、经济发展与水环境之间等[8-10]. 本文认为洪水过程的协同性是洪水形成过程的涨水、消退子系统之间的相干能力，表现为涨水、消退子系统在洪水形成过程中的协调或缓冲的性质. 协同学原理以系统的宏观行为为研究对象，引入影响系统演变过程的宏观参量——序参量，以描述系统的整体演化行为. 洪水过程作为一个整体和系统，序参量包含在涨水、消退子系统中,决定着该系统的演化过程. 因此，本文从洪水的涨水、消退子系统中提取反应洪水系统协同性的特征参数(宏观参量)，根据协同学原理，建立“洪水过程协同性评价模型”(Flood Process Synergy Degree Evaluation Model，FPSDE)，从洪水过程协同性角度分析洪水的变异性.

1 研究区概况

武江是北江流域第二大的一级支流，位于东经112°23′～113°36′、北纬24°46′～25°41′；主流发源于湖南省临武县三峰岭，流经湖南省的临武县、宜章县，于乐昌市老坪石上游3 km左右流入广东省的乐昌市，经乳源县、韶关市浈江区、武江区，与浈江水在韶关市沙洲尾汇合后注入北江；全河长260 km，流域面积7 097 km2，流速大，洪水传播时间快，流域地势高峻，植被较好，河流含沙量较少，其干流在广东境内比降较陡，平均比降1.27‰，是弯曲型的山区河流.

2 洪水过程协同性评价模型

本文以武江流域犁市站历史上的53场洪水为例，选取17个时段洪量作为序参量，利用协同学原理建立“洪水过程协同度评价模型(FPSDE)”，分析洪水过程的协同性是否发生改变. FPSDE模型的建立过程如下.

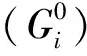
Pjj={p(jj)1,p(jj)2,…,p(jj)l,…,p(jj)K}，

(1)

其中，Pjj为第jj个子系统的序参量变量集合，p(jj)l(l[1,K])为第jj个子系统的第l个序参量变量，且K≥2. 序参量蕴含在洪水的涨水、消退子系统中，反映出洪水系统的演变过程. 本文选取洪峰点为这2个阶段的分割点，分割点以左为涨水段，分割点以右为消退段，从过程线中截取较为陡峻的部分涨水段、消退段，以时段洪量为洪水过程2个子系统的序参量. 根据本文提取到的53场洪水过程的涨水、消退子系统信息，结合2个阶段的共同特征，得出具体的序参量，即：2007年是53场洪水中消退子系统阶段历时最短的(为17 h)，而1980年是53场洪水中涨水子系统历时最短的(为20 h)，则取分割点开始向前推的17 h为涨水段，取分割点开始向后推的17 h为消退段. 因此，对于涨水子系统的序参量分别是：涨水开始第1小时的洪量，涨水开始第2小时的洪量，……，涨水开始第17小时的洪量(第17小时到达洪峰的分割点)；对于消退子系统的序参量分别是：消退开始第1小时的洪量(第1小时从洪峰的分割点出发)，消退开始第2小时的洪量，……，消退开始第17小时的洪量.

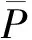
(2)

则第i场洪水过程子系统(sjj)序参量变量(p(jj)l)的有序度为[11]：

(3)

本文定义第i场洪水过程的涨水子系统评价函数为Z(Pjj)i，第i场洪水过程的消退子系统的评价函数为T(Pjj)i，由于2个子系统蕴含在一场过程中，所以其评价函数的构成形式相同. 利用贡献率计算模型，以各子系统中各指标贡献率占总贡献率大小的比为权重，建立相应的评价函数：

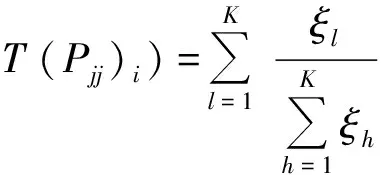
(4)

一般地，2个子系统的消停并涨的过程是相互促进、共同发展的，涨水子系统的评价函数和消退子系统的评价函数均反映各子系统的总有序度，然而各子系统均有自身的动态性和不平衡性，对于第i场洪水的整个洪水过程是否在2个子系统的协同作用下进行发展的，还有待计算2个子系统的协同度[10]：

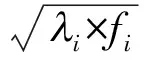
(5)

其中，Ci为2个子系统的协同度，i为协调系数，fi为洪水过程整体的综合评价函数. 利用物理学中的容量耦合系数模型计算协调系数：i=2；洪水过程整体的综合评价函数fi=α×Z(Pjj)i+β×T(Pjj)i；α、β为权系数，由于2个子系统的重要程度相同，因此α=β=0.5.

由式(5)得

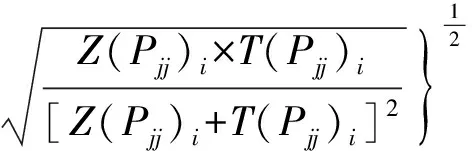
(6)

可知，C[0,1]，C值越大则系统协同发展程度越高，反之越低;当C=1时，系统的协同度达最大，协同性最强. 可见，可以根据Ci(i[1,…,n])的变化特征，判断流域洪水过程形成的协同一致性是否发生改变.

3 结果与分析

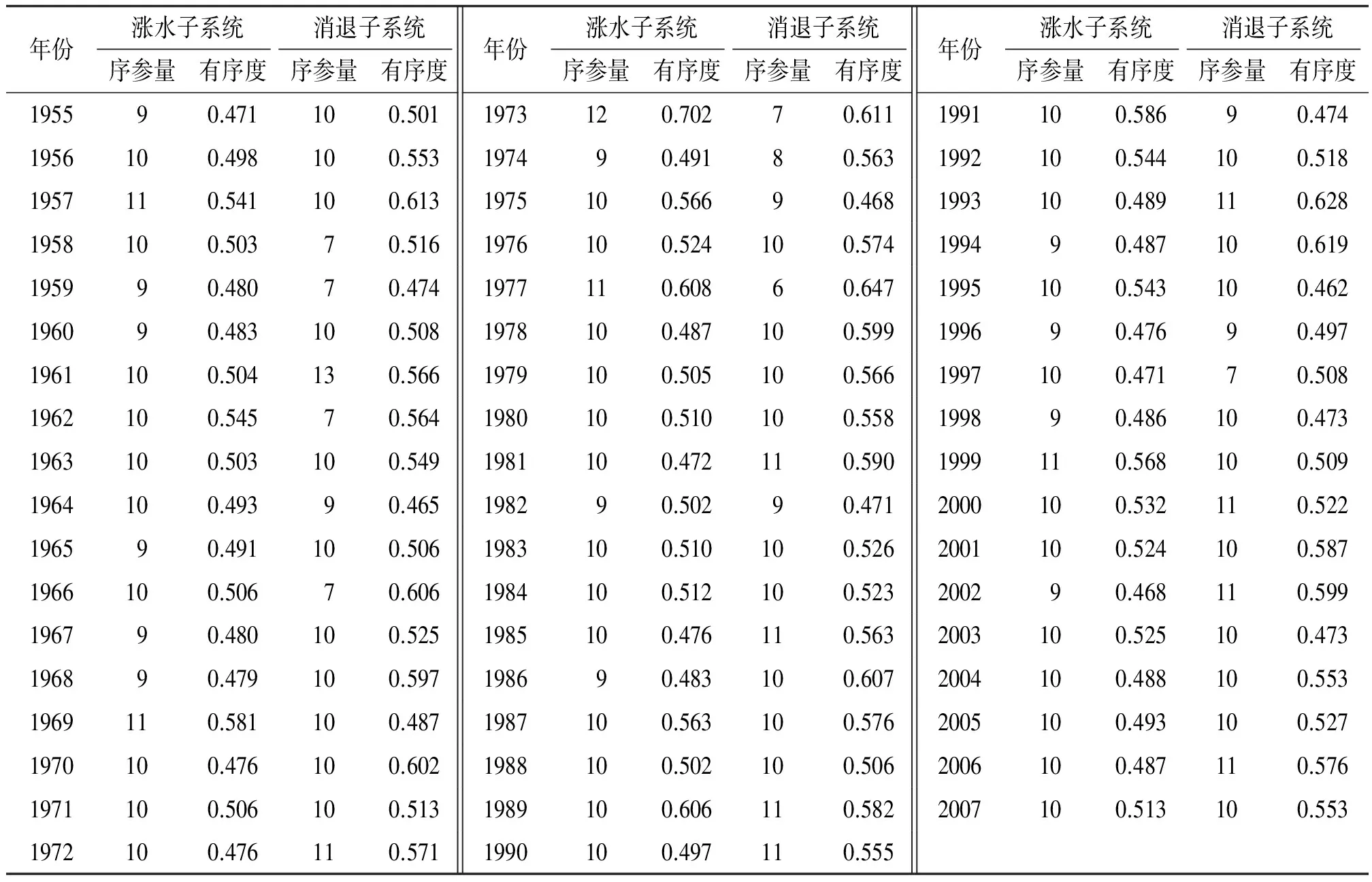
由表1可知，对于整个洪水过程，若以时段洪量作为洪水过程各子系统的序参量，涨水子系统序参量有序度的变化呈现先增加后减少的过程：随着时间的推移，序参量的有序度不断增加，当涨水子系统进行11小时后，序参量的有序度不断减小，说明第11小时时段洪量序参量对洪水过程的有序的贡献最大，而第1小时时段洪量的序参量对洪水过程的有序的贡献最小；相似地，消退子系统参量有序度的变化也呈现先增加后减少的过程：随着时间的推移，序参量的有序度不断增加，当消退子系统进行10小时后，序参量的有序度不断减小. 说明第10小时时段洪量序参量对洪水过程的有序的贡献最大，而第1小时和第17小时时段洪量的序参量对洪水过程的有序的贡献最小.

表1 武江流域犁市站洪水过程各子系统序参量的有序度Table 1 Order degree of order parameter in each subsystem of flood process at Lishi station of Wujiang River ×10-2

对同一场洪水过程而言，不同的序参量对洪水过程有序的贡献也不同，本文分别绘制武江流域犁市站53场洪水过程2个子系统17项序参量的变化图(图1和图2)，图中1～17项序参量与表1对应.

图1表明，涨水子系统第1项和第17项序参量的有序度均最小，序参量有序度最大值集中在第9～12项序参量之间，说明17项序参量中，第9～12小时时段洪量序参量对洪水过程的有序贡献最大;1957、1969、1973、1977、1999年涨水子系统17项序参量有序度曲线的走势与其他年份序参量有序度曲线的走势存在差异，且1973年的差异最大，存在差异的原因是由于这5场洪水的前10项序参量的有序度与其他年份对应的序参量有序度相比略小. 但是，涨水子系统各序参量不同年份的变化态势整体上较为一致，尤其是2000—2007年的8场洪水涨水子系统序参量有序度变化曲线走势几乎一致. 可见，武江流域犁市站53场洪水的涨水子系统相同的序参量对洪水过程有序的贡献基本相同.

图2表明，不同于涨水子系统，除20世纪80年代发生的10场洪水和本世纪发生的8场洪水在消退子系统各序参量在不同年份的变化态势较为一致外，其余年份发生的洪水在消退子系统中各序参量表现出的有序度变化曲线不尽相同. 说明武江流域犁市站53场洪水中消退子系统相同的序参量对洪水过程有序的贡献存在较大的差异.

由表2可知，各场洪水过程涨水子系统最大有序度对应的序参量大部分为第9、10项序参量，而1957、1969、1973、1977、1999年的5场洪水中除1973年第12项序参量的有序度最大外，其他4场洪水均为第11项序参量的有序度最大. 这5场洪水的表现(图1)为：涨水子系统各序参量的有序度变化曲线和其他年份曲线存在差异. 而各场洪水消退子系统最大有序度对应的序参量较为分散，第6～11项及第13项序参量都会成为某场洪水最大有序度对应的序参量. 因此，对于不同场洪水而言，相同序参量的有序度在不同的消退子系统中贡献情况不同，但在不同的涨水子系统中贡献情况大体一致. 53场洪水的涨水、消退子系统最大有序度之间的相关系数仅为0.067 0，说明2个子系统最大有序度之间的相关性不强.

图1 武江流域犁市站涨水子系统序参量的有序度

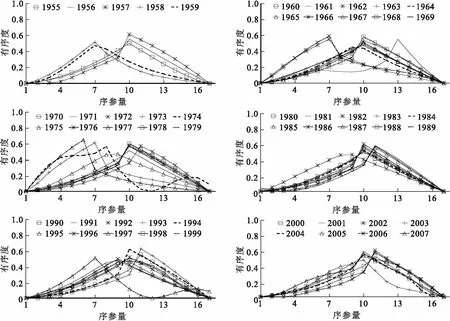
图2 武江流域犁市站消退子系统序参量的有序度

表2武江流域犁市站洪水各子系统最大有序度对应的序参量

Table 2 Order parameter corresponding to maximum order degree in each subsystem of flood process at Lishi station of Wujiang River

年份涨水子系统消退子系统年份涨水子系统消退子系统年份涨水子系统消退子系统序参量有序度序参量有序度序参量有序度序参量有序度序参量有序度序参量有序度195590．471100．5011973120．70270．6111991100．58690．4741956100．498100．553197490．49180．5631992100．544100．5181957110．541100．6131975100．56690．4681993100．489110．6281958100．50370．5161976100．524100．574199490．487100．619195990．48070．4741977110．60860．6471995100．543100．462196090．483100．5081978100．487100．599199690．47690．4971961100．504130．5661979100．505100．5661997100．47170．5081962100．54570．5641980100．510100．558199890．486100．4731963100．503100．5491981100．472110．5901999110．568100．5091964100．49390．465198290．50290．4712000100．532110．522196590．491100．5061983100．510100．5262001100．524100．5871966100．50670．6061984100．512100．523200290．468110．599196790．480100．5251985100．476110．5632003100．525100．473196890．479100．597198690．483100．6072004100．488100．5531969110．581100．4871987100．563100．5762005100．493100．5271970100．476100．6021988100．502100．5062006100．487110．5761971100．506100．5131989100．606110．5822007100．513100．5531972100．476110．5711990100．497110．555

由图3可知，涨水、消退子系统总有序度的均值分别为0.205、0.194. 根据FPSDE模型得：总有序度越大，系统有序度越高，反之越低. 因此，涨水子系统有序度最高的年份为1987年，其次为1986年，对应的总有序度分别为0.230、0.220；最低的年份为1991年，其次为1963年，对应的总有序度分别为0.075、0.155. 消退子系统有序度最高年份为2007年，其次为1981年，对应的总有序度分别为0.242、0.224；最低的年份为1963年，其次为1997年，对应的总有序度分别为0.092、0.133.

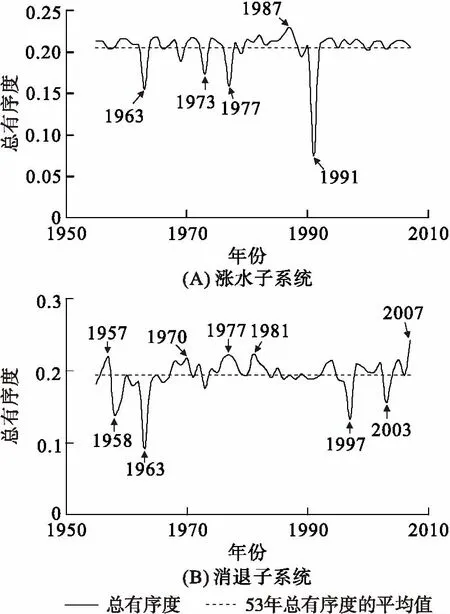
图3 武江流域犁市站历场洪水过程各子系统的总有序度

Figure 3 The total order degree of each subsystem in the flood hydrograph at Lishi station of Wujiang River

由图4可知：(1)武江流域从1955—2007年的53场洪水过程的协同度均值为0.446；(2)整体上，武江流域犁市站洪水形成过程的协同性有微弱的增强趋势，各场洪水的协同度值在均值上下波动，洪水形成过程的协同性较为一致，但存在较为偏离且低于均值的洪水过程，较明显的有8场，分别是1958、1959、1963、1973、1977、1991、1997、2003年，对应的协同度值分别是：0.411、0.428、0.345、0.418、0.433、0.345、0.409和0.422，表明这8场洪水的2个子系统的协同作用与其他年份相比较弱. 2007年协同度值最大，其次是1981年，协同度值分别为0.473、0.467；(3)根据洪水过程协同度评价模型，协同度越接近1，协同性越好，而本文中最大的协同度值仅为0.473，说明武江流域犁市站各场洪水形成过程的协同性较差. 这是由于武江流域属于山区河流，它的地形地势特征决定洪水陡涨陡落特性，导致洪水的消退子系统与涨水子系统的相干性不强，2个子系统的协调或缓冲性质不显著；(4)相关研究[13]表明，武江流域犁市站历史上发生大洪水的年份为：1968、1994、2002、2006年，这4场洪水不论是洪峰流量还是洪水强度，均比其他年份的洪水大. 然而，图4表明这4场洪水过程的协同度值分别为：0.463、0.464、0.461、0.451，与53场洪水过程协同度的均值0.446较为接近，不属于异样值. 说明尽管这4场大洪水的协同性不强，但是4场洪水形成过程未发生变异. (5)1963年和1991年的2场洪水形成过程的协同性发生了较为明显的变异. 这主要受涨水、消退子系统的总有序度影响：1991年的洪水涨水子系统总有序度最低，仅为0.075；1963年的洪水消退子系统的总有序度亦最低，仅为0.092.

图4 武江流域犁市站历场洪水过程的协同度

Figure 4 The synergy of each flood process at Lishi station of Wujiang River

可见，整体上尽管武江流域犁市站的洪水形成过程协同性较为一致，但各场洪水的涨水子系统与消退子系统的相干性不强，表现为洪水形成过程的协同性较差. 与此同时，1963年和1991年由于受到消退、涨水子系统总有序度的影响较为强烈，导致这2年洪水形成过程的协同性发生了较为明显的变异.

4 结论

本文依据协同学原理，建立“洪水过程协同性评价模型”，以武江流域犁市站历史上的53场洪水为例，从洪水过程协同性角度分析洪水的变异性. 研究结果表明：武江流域犁市站洪水形成过程的协同性有微弱的增强趋势，即武江流域犁市站的涨水子系统和消退子系统之间的协调或缓冲的能力增强，其中，2007年协同度值最大，其次是1981年，协同度值分别为0.473、0.467. 53场洪水中，低于平均协同度的8场洪水分别为：1958、1959、1963、1973、1977、1991、1997、2003年，这8场洪水的2个子系统的协同作用与其他年份相比较弱. 尽管武江流域过去发生了较大的洪水，从洪水的协同性角度来看，4场大洪水(1968、1994、2002、2006年)的协同性不强，但4场洪水形成过程未发生变异. 总体上，武江流域各场洪水的涨水子系统和消退子系统的相干性不强，表现为洪水形成过程的协同性较差，这是由于武江流域属于山区河流，它的地形地势特征决定洪水陡涨陡落特性，而在1963年和1991年洪水形成过程的协同性发生了较为明显的变异.

[1] RICHTER D B,BAUMGARTNER V J,BRAUN P D,et al. A spatial assessment of hydrologic alteration within a river network [J]. Regulated Rivers:Research & Management,1998,14:329-340.

[2] 陈晓宏,陈泽宏. 洪水特征的时间变异性识别[J]. 中山大学学报(自然科学版),2000,39(1):96-100.

CHEN X H,CHEN Z H. Recognition on the variability of hydrological time series[J]. ACTA Scientiarum Naturalium Universitatis Sunyatseni,2000,39(1):96-100.

[3] PINTER N,TOMAS R,WLOSINSKI J H. Assessing flood hazard on dynamic river [J]. EOS,2001,82(31):333-339.

[4] 陈晓宏,陈永勤. 珠江三角洲网河区水文与地貌特征变异及其成因[J]. 地理学报,2002,57(4):429-436.

CHEN X H,CHEN Y Q. Hydrological change and its causes in the river network of the Pearl River Delta[J]. Acta Geographica Sinica,2002,57(4):429-436.

[5] 陈晓宏,张蕾,时钟. 珠江三角洲河网区水位特征空间变异性研究[J]. 水利学报,2004(10):36-42.

CHEN X H,ZHANG L,SHI Z. Study on spatial variability of water levels in river net of Pearl River delta[J]. Shuili Xuebao,2004(10):36-42.

[6] WONG H,HU B Q,IP W C,et al. Change-point analysis of hydrological time series using grey relation method[J]. Journal of Hydrology,2006,324:323-338.

[7] 杨涛,陈永勤,陈喜,等. 复杂环境下华南东江中上游流域筑坝导致的水文变异[J]. 湖泊科学,2009,21(1):135-142.

YANG T,CHEN Y Q,CHEN X,et al., Evaluating hydrologic alternation along the East River basin,southern China,under the changing environment[J]. Journal of Lake Sciences,2009,21(1):135-142.

[8] 陈海军,邓良基,李何超,等. 城市化进程与耕地变化协同性研究—以成都市为例[J]. 中国农学通报,2010,26(1):312-316.

CHEN H J,DENG L J,LI H C,et al. Research on coordination between the urbanization development and cultivated land change in Chengdu City[J]. Chinese Agricultural Science Bulletin,2010,26(1):312-316.

[9] 李鹤,张平宇,刘文新. 1990年以来辽宁省环境与经济协调度评价[J]. 地理科学,2007,27(4):486-492.

LI H,ZHANG P Y,LIU W X. Assessment of coordination degree between environment and economy of Liaoning Province in China during 1990～2003[J]. Scientia Geographica Sinica,2007,27(4):486-492.

[10] 刘耀彬,李仁东,宋学锋. 中国城市化与生态环境耦合度分析[J]. 自然资源学报,2005,20(1):105-112.

LIU Y B,LI R D,SONG X F. Analysis of coupling degrees of urbanization and ecological environment in China[J]. Journal of Natural Resources,2005,20(1):105-112.

[11] 唐燕,李健. 工业城市资源再生产业与装备制造业经济协同度——以天津市为例[J]. 经济地理,2012,32(4):91-95.

TANG Y,LI J. Research on the economic synergistic degree between renewable resources industry and equipment manufacturing industry in industrial city[J]. Economic Geography,2012,32(4):91-95.

[12] 郝树荣,郭相平,张展羽. 投影寻踪分类模型在作物补偿效应评价中的应用[J]. 农业机械学报,2010,41(1):59-62;33.

HAO S R,GUO X P,ZHANG Z Y. Comprehensive evaluation on compensatory effects of water recovery after drought based on projection pursuit classification model.[J]. Transactions of the Chinese Society for Agricultural Machinery,2010,41(1):59-62;33.

[13] WANG L N,CHEN X H,SHAO Q X,et al. Flood indicators and their clustering features in Wujiang River,South China [J]. Ecological Engineering,2015,76:66-74.

Synergy Degree of Flood Process on Flood Changes

WANG Lina1*, CHEN Xiaohong2,3

(1. School of Geography Science, South China Normal University, Guangzhou 510631, China;2. Center of Water Resource and Environment Research, Sun Yat-Sen University, Guangzhou 510275, China; 3. Key Laboratory of Water Cycle and Water Security in Southern China of Guangdong Higher Education Institutes, Guangzhou 510275, China)

In order to analyze the variability of coordination of flood process, the Flood Process Synergy Degree Evaluation model has been established. The example is shown by the 53 floods in the Lishi station of Wujiang River. The order parameters of the flood process, including 17 flood volumes, are formed by the flood freshet and stage of flood process, respectively. The results show that the synergy of four floods (in the years of 1968, 1994, 2002, 2006), which brought greater economic losses, did not display variation in Wujiang River Basin. The performance of buffer and coordination, which appears in freshet stage and recession stage, is not strong in each flood process in Wujiang River Basin. But, there were the great variations of synergy, which occurred in 1963 and 1991.

freshet stage of flood process； recession stage of flood process； flood system； synergy degree； order parameter

2016-04-05 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(41501021,51210013)；国家科技支撑计划项目(2012BAC21B0103)；水利部公益项目(201201094, 201301002-02)

*通讯作者:汪丽娜，副教授，Email:linawang2004@163.com.

TV122+.5

A

1000-5463(2017)06-0077-07

【中文责编：庄晓琼 英文审校：叶颀】