Bogoliubov-de Gennes对角化与Schur分解方法的等价性

张 雨， 黄镇华， 李 铭

(华南师范大学物理与电信工程学院， 广东省量子调控与材料重点实验室，广州 510006)

Bogoliubov-de Gennes对角化与Schur分解方法的等价性

张 雨， 黄镇华， 李 铭*

(华南师范大学物理与电信工程学院， 广东省量子调控与材料重点实验室，广州 510006)

以Kitaev的一维量子线模型为例，分别利用传统的Bogoliubov-de Gennes(BdG)对角化方法和Schur分解方法求解该模型的本征能量以及本征波函数，从理论分析和数值计算方面对2种方法进行对比. 结果表明，BdG对角化方法得到的准粒子能量是能量本征值的2倍，而Schur分解方法可以直接得到准粒子能量. 两者数值计算结果一致. 另外，在确定的参数下，2种方法得到的准粒子算符对初始的费米子算符的展开系数只相差一个常数相因子. 所以，最后的结论是BdG对角化跟Schur分解两种方法是等价的.

BdG对角化方法； Schur分解； Majonara费米子； 粒子-空穴对称； 拓扑绝缘体

求解一个哈密顿量的本征值和本征函数，人们通常采用的数值计算方法是Bogoliubov-de Gennes(BdG)对角化方法[1-4]. 问题是在某些情况下该方法可能需要扩大自由度的维数[5]，从而产生伪态. Kitaev[6]在2000年提出一个模型，在三维超导体表面的量子线两端呈现Majonara零能模. 他没有利用传统的BdG对角化方法，而是用费米子产生湮灭算符构造结果Majonara费米子算符，得到具有斜正交矩阵形式的哈密顿量，然后实行分块对角化. 这个分块对角化正好可以通过Matlab的Schur分解来实现[7]. 目前Kitaev方法应用较少，多数情况采用BdG对角化方法直接对角化. 一个疑问是：这两种方法得到的结果是否一致呢？本文以Kitaev模型为例，首先从理论上对BdG对角化和Schur分解两种方法进行对比，然后通过数值计算比较两种方法得到的本征能量以及波函数. 研究结果表明：两种方法是等价的，并且BdG对角化方法更简单.

1 研究方法

1.1 BdG对角化方法

Kitaev模型的哈密顿量可以表示为[7]:

(1)

其中，t是最近邻格点跳跃幅度，μ是化学势，Δ=|Δ|eiθ是超导配对势.

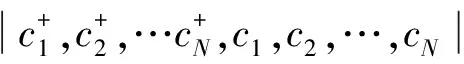
H=C+hC,

(2)

其中，

(3)

对矩阵h进行对角化得到h=SES+. 这里的S是引入的一个幺正矩阵.E是一个对角矩阵对角元素为(±E1±E2…)，且从小到大排序. 矩阵S的每一列为相应能量本征值所对应的本征矢. 把h=SES+代入前面的哈密顿量中，并且设

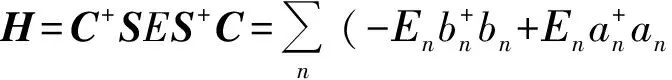
(4)

新构造的准粒子算符采用原费米子算符展开为：

(5)

(6)

下面证明，这两套费米子算符的一致性. 对于矩阵h的任意一个能量本征值En，本征矢量满足下列BdG方程[8]：

(7)

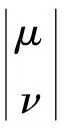
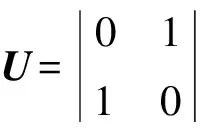
对BdG方程(7)等号两边进行幺正变换，重新整理后得到如下形式：

(8)

(9)

(10)

将其代入新费米子算符(5)得:

(11)

所以，本征值为负的伪态，可以消除. 于是，哈密顿量式(4)变为：

(12)

可见，通过BdG对角化方法所得能量的2倍才是真正的准粒子能量本征值.

1.2 Schur分解方法

采用Schur分块法求解Kitaev模型. 首先用Majonara费米子算符改写Kitaev模型的哈密顿量. Majonara费米子算符定义为：

(13)

满足Majonara费米子的反对易关系{γi,γj}=2δij，将式(13)代入式(1)得：

(14)

这一哈密顿量可以写成如下矩阵形式：

(15)

其中，A是2N×2N的实反对称矩阵(Aj，i=-Ai，j) 实反对称矩阵的非零本征值是纯虚数，并且正负成对出现[6,11]，设为±iεn，εn≥0. 所以，A可以写成如下形式：

A=WTBW,

(16)

其中，

(17)

W是2N×2N的实正交矩阵，WWT=1. 该矩阵可用Matlab的Schur子程序计算. 将式(16)代入哈密顿量可以得到：

(18)

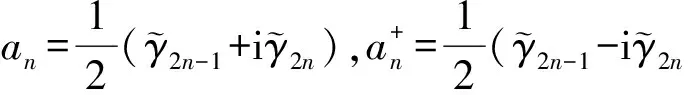
(19)

得到对角化的哈密顿量：

(20)

其中，

(21)

式中，

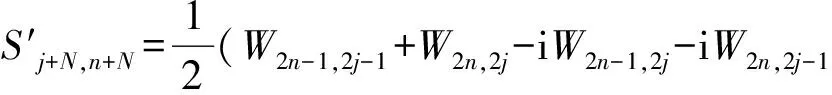
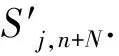
2 结果与讨论

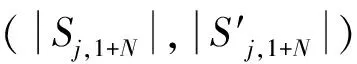
2.1 准粒子能量

首先，按照Schur分解和BdG对角化两种方法计算准粒子能量(图1)，采用Schur分解方法得到的准粒子能量跟BdG对角化方法得到的2En完全一致. 另外，这里还出现了一个零能量E=0，与其他能量之间有一个明显的能隙. 这个零能量态就是马约拉纳零模[7,12-13]，这也正是Kitaev在该玩具模型中预言的[6]，其零模的稳定性受拓扑保护.

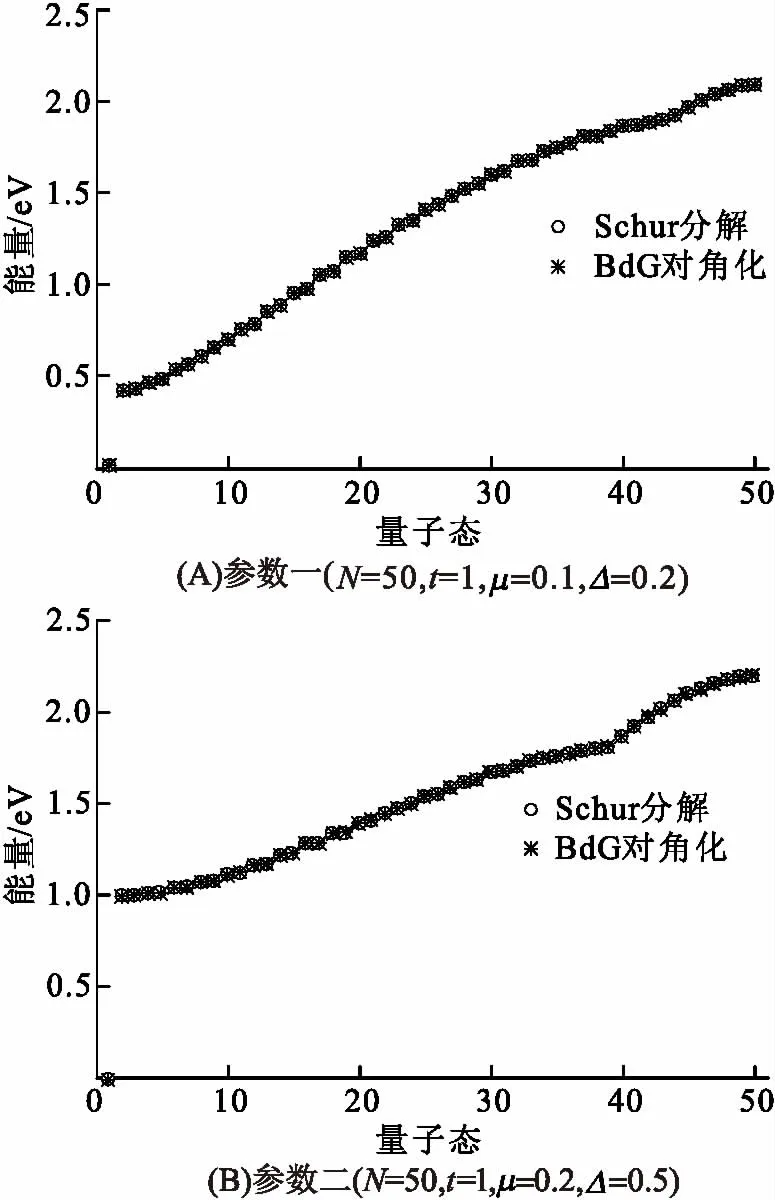
图1 两种方法在不同参数下计算得到一维链上电子的准粒子能量

Figure 1 Quasiparticle energies of electrons on a one-dimensional chain by two methods with different parameters

2.2 零模准粒子的展开系数绝对值及相对相位角

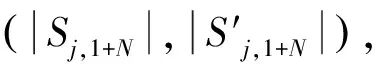
由于量子力学波函数的位相不确定性，零模准粒子的展开系数可以存在一个常数相因子的差别(相对相位角). 为了检验2种方法得到的展开系数是否只是相差一个常数相因子，进一步计算了所有格点上2种方法得到的展开系数之比的相位角(图3). 可见，在同一组参数下，不同格点上的相位角是完全相同的. 这表明用2种数值计算方法得到的波函数只存在着常数相因子的差别.

图2 两种方法求不同参数下零模准粒子产生算符展开系数的绝对值

Figure 2 Absolute values of expansion coefficients of zero mode quasi-particle annihilation operator by two methods with different parameters

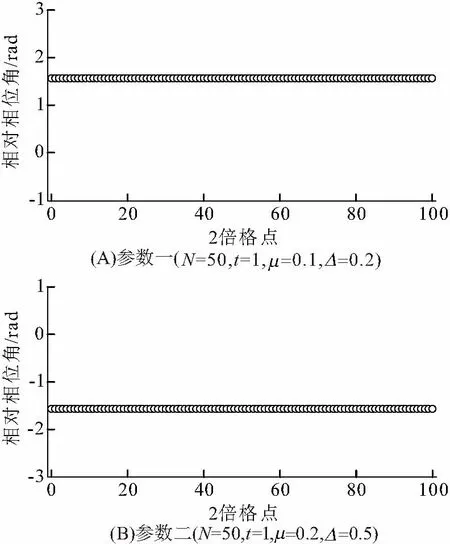
图3 Schur分解法与BdG对角化方法在不同参数下求得零模准粒子产生算符展开系数的相对相位角

Figure 3 Relative phase angles of expansion coefficients of zero mode quasi-particle annihilation operator between Schur and BdG

2.3 第一激发态准粒子算符展开系数及相位角

对比两组不同的参数下用2种方法得到第一激发态能量相应准粒子产生算符的展开系数绝对值(图4)以及展开系数相差的相位角(图5). 由图4可以看出，相同参数下2种方法得到的第一激发态能量对应的准粒子算符其展开系数绝对值相同. 由图5可以看出两组参数下2种方法得到第一激发态能量对应的准粒子算符其展开系数之间相差的相位角都是零，也就是说此时2种方法得到的准粒子算符的展开系数之间不存在常数相因子的差别，二者完全相同. 所以，数值计算结果表明，BdG对角化和Schur分解2种数值计算方法在求解同一个一维拓扑超导体Kitaev模型的本征值和本征函数时是等价的. 另外，对2种方法进行进一步分析发现各有其优点：首先，BdG对角化方法在求解本征函数和本征能量的计算过程中更加简洁方便. 值得注意的是，BdG对角化的方法直接得到的能量的2倍才是真正的准粒子能量本征值. 其次，由于马约拉纳费米子更像是半个狄拉克费米子，因此采用Schur分解方法在处理马约拉纳费米子行为问题时则更加直观清晰. 综上所述，可以根据处理问题的不同而选择合适的方法进行计算分析，从而达到事半功倍的效果.

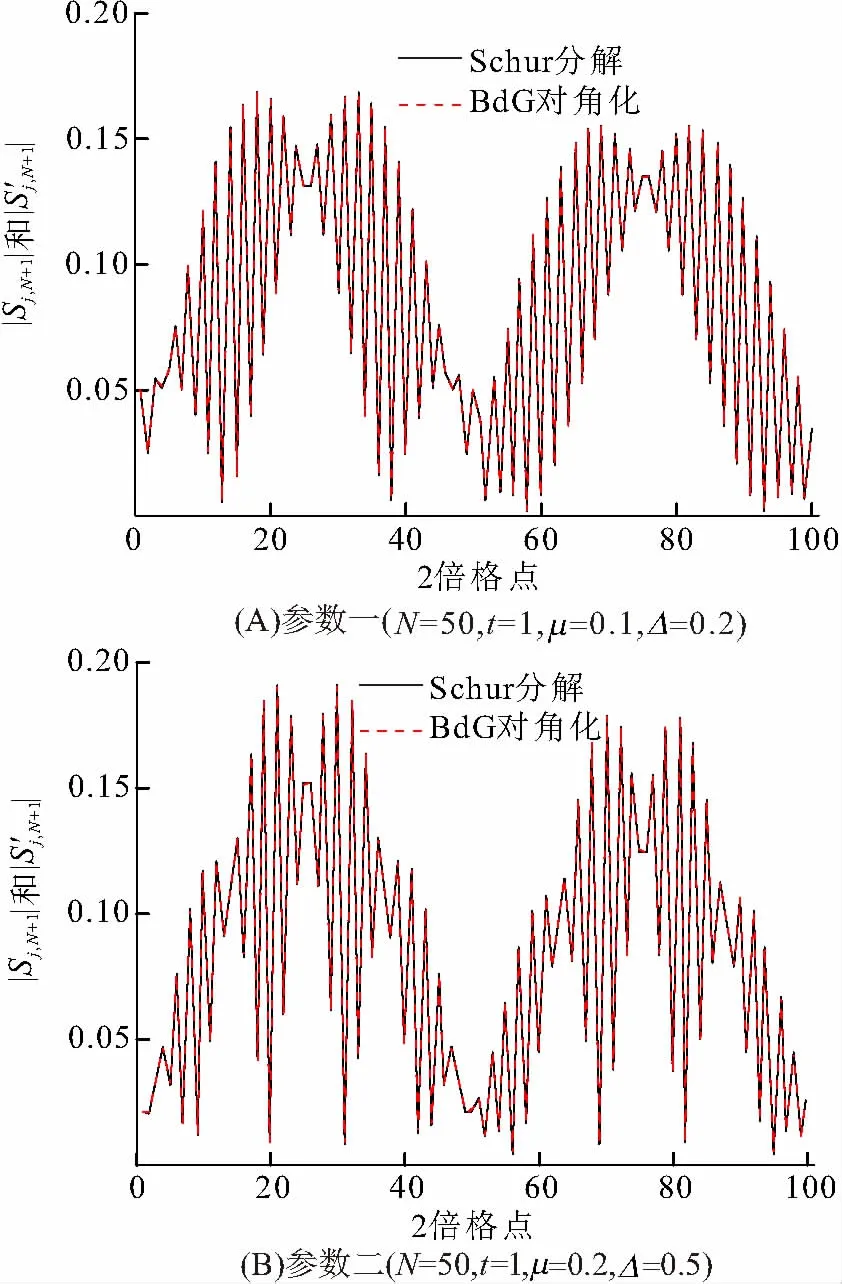
图4 两种方法求不同参数下第一激发态准粒子产生算符的展开系数绝对值

Figure 4 Absolute values of expansion coefficients of quasi-particle annihilation operator of the first excited state by two methods with different parameters

图5 Schur分解法与BdG对角化方法在不同参数下求得第一激发态准粒子产生算符展开系数的相对相位角

Figure 5 Relative phase angles of expansion coefficients of quasi-particle annihilation operator of the first excited state between Schur and BdG with different parameters

3 结论

通过理论分析和数值计算验证了BdG对角化和Schur分解2种数值计算方法的等价性. 由于超导配对相的存在，用BdG对角化方法求解哈密顿量不得不扩大1倍自由度个数，但最后在粒子-空穴对称的前提下自由度两两重合，准粒子能量正好是能量本征值的2倍. Schur分解法得到的能量本征值直接给出准粒子能量. 数值计算结果表明，2种方法得到的准粒子能量是完全一致的. 2种方法得到的准粒子算符对初始费米子算符的展开系数只有1个常数位相因子的差别. 所以，这2种方法是等价的.

[1] KURITA Y,KOBAYASHI M,MORINARI T,et al. Spacetime analog of Bose-Einstein condensates: Bogoliubov-de Gennes formulation[J]. Physical Rewiew A,2009,79:043616.

[2] OZANA M,SHELANKOV A,TOBISKA J. Bogoliubov-de Gennes versus quasiclassical description of josephson structures[J]. Physical Review B,2002,66(5):340-351.

[3] SHANENKO A A,CROITORU M D,PEETERS F M. Oscillations of the superconducting temperature induced by quantum well states in thin metallic films: numerical solution of the Bogoliubov-de Gennes equations [J]. Physical Review B,2007,75: 014519.

[4] BJÖRNSON K,BLACK-SCHAFFER A M. Probing vortex Majorana fermions and topology in semiconductor-superconductor heterostructures[J]. Physical Review B,2015,91(21):1610-1625.

[5] BJÖRNSON K,BLACK-SCHAFFER A M. Majorana fermions at odd junctions in a wire network of ferromagnetic impurities[J]. Physical Review B,2019,94:100501.

[6] KITAEV A Y. Unpaired Majorana fermions in quantum wires[J]. Physics-Uspekhi,2001,44:131-136.

[7] CHEN L,LI M W,HUANG J H,et al. Majorana zero modes on a one-dimensional chain for quantum computation[J]. Physical Review A,2014,90(1):4804-4810.

[8] QU C,ZHENG Z,GONG M,et al. Topological superfluids with finite-momentum pairing and Majorana fermions[J]. Nature Communications,2013,4(10):2710.

[9] GIRVIN S M. Particle-hole symmetry in the anomalous quantum Hall effect[J]. Physical Review B:Condensed Matter,1984,29(10):6012-6014.

[10] LIN R,WANG Z. A brief review on Majorana bound states in topological superconductors[J]. Science China Physics,Mechanics & Astronomy,2016,59(7):677401.

[11] KITAEV A. Anyons in an exactly solved model and beyond[J]. Annals of Physics,2005,321(1):2-111.

[12] SANTOS L,NISHIDA Y,CHAMON C,et al. Counting Majorana zero modes in superconductors[J]. Physical Review B,2011,83(10):1161-1171.

[13] SATO M,FUJIMOTO S. Topological phases of noncentro symmetric superconductors: edge states,majorana fermions,and the non-abelian statistics[J]. Physical Review B,2008,79:094504.

Equivalence between Bogoliubov-de Gennes Diagonalization and Schur Decomposition

ZHANG Yu， HUANG Zhenhua， LI Ming*

(Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China)

The Equivalence between the Bogoliubov-de Gennes (BdG) Diagonalization method and the Schur decomposition has been verified through numerical computations to the Kitaev model of a one-dimensional quantum wire. Comparisons between two methods have been conducted in terms of theoretical analysis and numerical computation. The quasipartical energies obtained from the BdG method are twice the eigenenergies but the Schur decomposition gives the quasipartical energies directly. The numerical results show that quasipartical energies from the two methods are consistent with each other perfectly. In addition, the expansion coefficients of the quasipartical operators from two methods have only a constant phase in difference. The final conclusion is drawn that BdG diagonalization method and Schur decomposition are equivalent.

BdG diagonalization; Schur decomposition; Majonara fermions; particle-hole symmetry; topological insulator

2017-01-08 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

广东省教育厅团队项目(C1085031)

*通讯作者:李铭，教授，Email:wliming@scnu.cn.

O41

A

1000-5463(2017)06-0012-05

【中文责编：谭春林 英文审校：肖菁】