三角网格的融合与优化及其在电磁散射计算中的应用

丁娟娟，孙玉鑫，刘 鹏

(复旦大学 电磁波信息科学教育部重点实验室,上海 200433)

三角网格的融合与优化及其在电磁散射计算中的应用

丁娟娟，孙玉鑫，刘 鹏

(复旦大学 电磁波信息科学教育部重点实验室,上海 200433)

为实现数值计算中复合模型的三角网格融合、优化电磁散射计算，提出基于三角形求交、面元内角控制的网格模型融合与优化算法．通过两个独立模型中三角面元的交点计算和模块内点云的Delaunay剖分，获得初始融合网格，再通过查找、消除畸形面元来优化融合后的网格．一系列模型的测试表明，在保持网格采样信息与几何外观的前提下，本文所提出的算法可稳健、有效地实现不同网格密度、不同结构特征的三角面元模型融合，去除畸形面元减少网格面元数目．

网格融合； Delaunay剖分； 畸形三角面元； 电磁散射计算

三角面元广泛应用于数值建模，常用于计算流体力学、计算电磁学等众多领域．在数值模型中，不同几何体的网格拼接处一般是物理场的耦合区，为保证数值计算的精度和稳定性，往往对拼接处的网格单元形状有较高的要求．虽然单一模型的三角面元网格建模已实现工程化，有大量成熟的软件，但是不同软件或不同建模方法生成的模型之间往往需要单独进行网格融合或网格拼接，例如建筑物模型与地表模型，舰船模型与海面模型等，在这些领域网格融合算法显得尤为重要．

舰船与尾迹的网格模型由不同的算法或软件独立生成的，网格的节点密度和结构特征存在较大差异．为准确研究舰船与海面复合场景的电磁散射，需要考虑船体与海水交接处的二面角强散射机制．因此，作为本文研究的重点，网格融合算法的正确性、稳健性以及融合后网格的品质等因素，将直接影响到后续的电磁散射计算分析与雷达成像的工程应用．

三角形面元网格的融合拼接方法主要有3类[1]： 第1类是基于裁剪的方法，即利用一片网格去裁剪另外一片网格，然后在公共边界上生成新的三角形单元，将两个模型的网格融合在一起，如Turk和Levoy等的算法[2]．该方法的缺点是因为裁剪，公共边界处会产生大量的细小三角形，并且该方法只利用了重叠区一片网格中的顶点，另一片网格上的顶点则被完全抛弃．因此对于存在大交叠区域的网格而言，无法同时利用两片网格的重叠区进行顶点校正．第2类是基于补洞的方法，即首先将重叠区的三角形全部删掉，然后通过补洞的方法重新生成重叠区的三角形．如Ruding提出的先去除N-环相交区再重建交叠区的方法[3]．该方法对于交叠区较小的的网格非常适用，但对于存在大交叠区域的网格，虽然可通过径向基函数重新生成重叠区顶点，但新生成的顶点很难反映模型的实际形状．第3类是基于微分网格变形的方法，如利用泊松方程[4]、拉普拉斯坐标[5]等方法．这类方法需要指定一个准确的边界，边界的定位精度对融合结果影响很大；但是大范围复杂交叠区的拼接往往难以确定精确的融合边界．

本文通过求取两个模型三角面元的所有交点，克服了第1类方法不完全采样的缺点，采用基于散乱点云的二维Delaunay剖分[6-7]，得到散乱点集的三角剖分结果．与第3类方法相比，文中网格融合的算法无需附加条件，局部区域重新剖分与否，完全取决于交叠区网格三角面元的交点情况，交叠区面元的数量仅影响计算速度，同时克服了第2类方法在大交叠区域模型失真的困难．通过去除融合过程中产生的畸形三角面元，优化融合后的网格，且保持融合区网格的采样信息与几何外观．

1 基本定义

定义1三角网格： 用三元组集合F：{v,e,f}来描述，其中v：{v1,v2，…，vn}表示点集合e：{e1,e2,…,en}表示边集合，f： {f1,f2,…，fn}表示三角形集合．

定义2畸形三角形： 一个或两个内角小于阈值δ的三角形，如图1所示(工程中一般取δ=15°)，小于δ的内角称作病态角．

定义3两个网格的融合： 指当两个网格模型在三维空间上相交时，将二者的网格数据重新编排为一个网格体，节点、面元都有唯一编号，且拓扑关系相应改变．

2 融合与优化策略

为实现由独立模型到复合模型的整体转换，需将原来两个互相独立的网格系统，合并成一个网格系统，网格系统中的每个三角面元、每个节点都有唯一的编号，面片之间拓扑关系正确，网格质量满足数值计算要求．

2.1 三维点云的平面投影及剖分

在本文融合算法中，待融合区网格三角面元交点产生三维点云，先将点云投影到二维空间，如图2所示，再将三维点云绕定轴r逆时针旋转α角到x-y面，得到投影点集．对投影点集作平面域的Delaunay剖分，构建出的二维投影点拓扑连接关系，与原三维点云拓扑连接关系相同．

2.2 三角网格的融合

三角网格F1、F2，融合算法流程如图3所示： 融合区域M1、M2分别有P、Q个面元，经正(红色虚线框)、反(绿色虚线框)两次融合，将每个面元区的三维点集投影到x-y面进行Delaunay剖分，生成每个面元区新的网格拓扑；最后合并M3与M4，并进行网格节点与面元查重．对于电磁散射计算等仅需表面网格的情况，还应去除融合网格内部不可见部分．

图3 三角网格融合算法流程图Fig.3 Flow chart of the merging algorithm for triangular meshes

2.3 网格优化算法

三角网格优化目前比较成熟的准则有以下5种： Thiessen区域准则、最小内角最大准则、圆准则、ABN准则和PLC准则[8-9]．就三角形形态来说，等边三角形最接近圆，是品质最高的三角形,是三角面元的最高优化目标[10]．

文献[11]提出一种改善畸形三角形的方法，通过删除畸形三角形和调整生成点的相对位置来实现，然而不能完全满足控制内角范围的要求．为解决任意两个三角网格模型融合后，局部网格畸形三角面元多而集中的问题，本文提出一种新方法，即通过控制畸形三角面元3个内角的大小，来改善三角网格的质量．

以等边三角形为标准可定义三角形正则度如下[10]：

R(η)=2(cosA+cosB+cosC-1)，

(1)

其中A、B、C分别是三角形的3个内角．只需知道三角形一个内角，即可计算其正则度：

(2)

其中X是某个内角，X从0到π变化时三角形的正则度如表1所示．

表1 三角形正则度R(X)随X变化规律Tab.1 The relationship between the triangle regularity R(X) and X

根据正则度的定义，可进一步定义如下的三角网格品质因子Q：

(3)

即网格中所有三角面元的正则度均值决定了网格的品质因子，式(3)中：N是网格模型中三角面元的数量；X是第i个三角形的某个内角；Ri(X)是第i个三角形的正则度．如式(2)所示．品质因子越大，说明网格中三角面元的正则度越大、越接近等边三角形，网格的质量越高．

本文选取的优化阈值为15°，即判定内角小于15°的三角面元为畸形面元．网格优化关键在于恰当处理畸形面元，需综合考虑畸形面元的相邻面元．优化原理如图4所示： 浅蓝的畸形三角面元，点v1对应内角小于15°，其对边的中点为vn．为消除畸形面元，需删除节点v6、v7，依次连接点vn与节点v1～v5，得到不含畸形面元的新的网格结构，如图4(b)所示．图5(a)为存在多个畸形面元的网格，图5(b)为本文算法优化后的结果，不再有畸形三角面元，优化前网格的品质因子为0.331，优化后为0.718，网格品质显著提高．

3 融合实例及应用

3.1 融合优化实例

为进一步验证本文算法的有效性，本节进行复杂模型的融合测试： 第1例为球面和随机粗糙面，如图6(a)所示；第2例为舰船与海面尾迹，如图6(b)所示；第3例为球面和立方体表面，如图6(c)．分析3例融合结果，模型的几何特征得以很好地保存，基本未发生几何形变，综合考虑工程计算的需求和融合区的几何特征，合理选取优化角度，还可进一步减小网格的几何失真．为比较优化前后网格面元的内角分布情况，图6(d)以第2例模型为例，统计面元内角在0°～180°的分布．优化前网格模型存在大量内角在0°～15°的三角面元，而优化后已完全消除．

图6 复杂模型优化前后的结果对比Fig.6 Comparison of the merged meshes of complex models before and after optimization

表2是图6中(a)、(b)、(c)模型融合优化前后面片数和网格品质因子的对比，其中，舰船与尾迹的融合区域面元数量由原来的3473个减少到2410个，面元数减少30.6%．在传统的融合算法中，基于顶点融合的方法为保持几何外观，融合后模型的面片只增不减；而基于裁剪补洞的融合方法需要生成更多的点和面片，以弥补裁减交叠区导致的几何失真，二者都不利于提高计算效率．在本文融合算法中，生成点为三角形的交点，因此融合过程不改变模型的几何特征．

表2 融合前后面片数与网格品质因子的对比Tab.2 The comparison of face numbers and mesh quality

3.2 二面角模型RCS算例

边长为a、b，公共边长l，夹角2β的四边形二面角单站RCS由式(4)给出，Sa,Sb是二面角一次散射PO解，Sab、Sba是a→b和b→a的二次散射，

(4)

根据物理光学法(PO)散射计算公式[12]，在E极化下：

(5)

其中：

(6)

(7)

其中：α=π-3β；tanγ=bsin 2β/(α-bcos 2β)；波数k=2π/λ．在H极化下，用-sin(3β∓θ)代替式(5)中的sin(3β±θ)．

图7(a)中四边形平板a×b=12cm×12cm，所形成二面角l=12cm，夹角2β=90°，平面波E极化，频率为10GHz,入射角θ从-45°～45°．图7(b)中蓝点为实测数据[13]，红虚线为未融合的计算结果，黑实线为融合二面角的PO计算结果，融合二面角计算结果与实测数据吻合．±40°附近二面角散射较强，由于两个平板的融合区很小，未融合的网格仅在±40°附近产生误差．

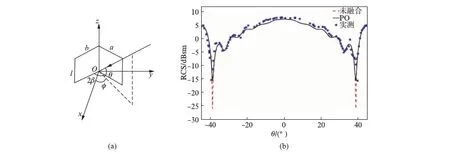
图7 二面角RCS(10GHz)Fig.7 RCS of the Dihedral(10GHz)

3.3 舰船与尾迹融合及RCS计算

舰船模型根据典型驱逐舰的构造建模，如图8(a)所示.500m×500m的尾迹模型如图8(b)所示，图中浅黄区域所示为待融合网格区域，网格品质因子Q为0.667．融合后模型如图8(c)，Q提高到0.826．

图8 舰船与尾迹的融合与优化Fig.8 Merge and optimization of ship and wakes

为进一步比较融合模型的计算结果，将本文与文献[14]中舰船与海面模型的双站RCS进行对比．具体计算参数如下： 雷达入射平面波频率为5GHz，θi=45°，φi=0°，HH极化；双站散射角θs=-90°～90°，φs=0°．结果如图8(d)所示，红虚线为本文模型融合前的结果，黑实线为融合后的结果，蓝实线为文献[14]的结果，可见由于二面角的强散射机制，融合与未融合模型在-90°～-70°、-30°、-10°附近区别较大．本文结果与文献[14]趋势基本相同．由于舰船结构、随机粗糙海面以及尾迹模型等方面的差异，二者的双站散射在某些角度存在差别．

4 结束语

本文介绍了一种复杂三角网格模型的融合方法．算法克服了补洞拼接法在大交叠区域的模型失真和裁剪方法的不完全采样的缺点．算法与网格交叠区的大小无关，不受附加条件限制，可以优化、去除网格融合过程中产生的畸形三角面元，并保持网格的采样信息与几何外观．

[1] 邹北骥，周浩宇，王磊等.大交叠区域的三维网格的融合与拼接 [J].电子学报，2012，40(5)： 1005-1010.

[2] TURK G, LEVOY M. Zippered polygon meshes from range images [C]∥. Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques(SIGGRAPH’94). Oriando, FL, USA, 1994： 311-318.

[3] RUDING L, JEAN-PHILIPPE P, ALEXEI M,etal. Merging enriched finite element triangle meshes for fast prototyping of alternate solutions in the context of industrial maintenance [J].CADComputerAidedDesign, 2010,42(8)： 670-681.

[4] YU Y, ZHOU K, XU D,etal. Mesh editing with poisson-based gradient field manipulation [J].ACMTransactionsonGraphics, 2004,23(3)： 644-651.

[5] SORKINE O. Differential representations for mesh processing [J].ComputerGraphicsForum, 2006,25(4)： 789-807.

[6] VORONOI G. Nouvelles applications des parameters continues a la theorie des formes quadratiques Deuxieme memorie： recherches sur les parallelloedres primitives [J].JournalFurDieReineundAngewandteMathematik, 1908,134： 198-287.

[7] LEE D T, SCHACHTER B J. Two algorithms for constructing a delaunay triangulation [J].InternationalJournalofComputerandInformationSciences, 1980,9(3)： 219-242.

[8] PARK S C. Polygonal extrusion [J].TheVisualComputer, 2003,19(1)： 38-49.

[9] WANG C C L, YUEN M M F. Sketch based mesh extrusion with remeshingtechniques [J].ProceedingsoftheASMEDesignEngineeringTechnicalConference, 2001,1： 731-738.

[10] 刘泗岩,廖文和,刘浩.基于内角余弦和的三角形正则度评定与网格优化 [J].机械科学与技术，2007，26(4)： 420-423.

[11] 王群,李爱平,马淑梅.局部网格狭长三角形的品质改善及实现 [J].同济大学学报(自然科学版)，2004，32(11)： 1508-1511.

[12] KNOTT E F. RCS reduction of dihedral corners [J].IEEETransactionsonAntennasandPropagation, 1977,25(3)： 406-409.

[13] ANDRADE L A, NOHARA E L, PEIXOTO G G,etal. Backscattering analysis of flat plate and dihedral corner reflectors using PO and comparison with RCS measurements in anechoic chamber [J].IEEEMTT-SInternational, 2003,2： 719-724.

[14] ZHAO Y, ZHANG M, ZHAO Y W,etal. A bistatic SAR image intensity model for the composite ship-ocean scene [J].IEEETransactionsonGeoscience&RemoteSensing, 2015,53(8)： 1-9.

AnAlgorithmforMergingandOptimizingtheTriangularMeshesofShipandSeaSurface

DINGJuanjuan,SUNYuxin,LIUPeng

(KeyLaboratoryforInformationScienceofElectromagneticWaves,FudanUniversity,Shanghai200433,China)

This paper presents a new method to merge and optimize the triangular meshes of ship and sea surface for numerical calculations. The method is divided into three steps： Firstly, identify the intersected nodes of the ship mesh and the sea mesh. Then, obtain the initial merged mesh by performing the Delaunay triangulation for the nodes in the intersected region. Finally, optimize the merged mesh by eliminating the abnormal triangles and renumbering the remaining nodes and elements. A series of examples show that this method is capable of merging the meshes with different structure and density, such as those of the ship, the rough sea surface, and the ship wakes. The method can not only run without any auxiliary conditions, but also improve the quality of the merged mesh.

mesh merge; Delaunay triangulation; abnormal triangles; electromagnetic scattering calculation

0427-7104(2017)06-0712-07

2017-02-21

国家自然科学基金(61179022)

丁娟娟(1991—)，女，硕士研究生；刘 鹏，副教授，通信联系人，E-mail： pliu@fudan.edu.cn.

TP391.7

A