基于正交试验法的重力锚基坑岩土参数敏感性分析

，，，，

(1.中国科学院 地质与地球物理研究所，北京 100029；2.重庆市交通委员会工程质量安全监督局，重庆 400060；3.中国电建集团 中南勘测设计研究院有限公司，长沙 410014；4.中交一公局驸马长江大桥一分部，重庆 万州 404000)

基于正交试验法的重力锚基坑岩土参数敏感性分析

冉涛1，毛江南2，梅松华3，王巍伟4，谭利华4

(1.中国科学院 地质与地球物理研究所，北京 100029；2.重庆市交通委员会工程质量安全监督局，重庆 400060；3.中国电建集团 中南勘测设计研究院有限公司，长沙 410014；4.中交一公局驸马长江大桥一分部，重庆 万州 404000)

为了探究重力锚基坑变形过程中的岩土参数敏感性，以重庆万州驸马长江大桥北岸重力锚基坑作为研究对象，首先基于正交试验法设计计算方案，采用有限差分软件FLAC3D对基坑开挖变形进行数值计算。然后对计算结果进行极差分析和方差分析。结果表明：极差分析和方差分析识别出的影响基坑开挖变形的主要岩土参数均为全风化层的弹性模量E1、泊松比μ1、黏聚力c1、内摩擦角φ1以及强风化层的弹性模量E2；结合基坑开挖试算结果综合确定的反演目标参数为全、强风化层的弹性模量E1和E2。研究结果为后续的位移反分析奠定了基础，以及为控制基坑开挖变形提供了施工指导建议，同时还为类似工程的敏感性分析问题提供了借鉴方法。

深基坑工程；敏感性分析；岩土参数；正交试验法；统计分析

1 研究背景

数值计算已经被广泛应用于边坡工程、隧道工程和基坑工程等地表和地下工程的设计和评价中，众所周知，岩土体力学参数是影响岩土工程数值计算结果准确性的最重要因素之一。目前，确定岩土力学参数的方法主要有室内试验、现场试验、工程类比以及反分析方法等。然而，由于受到试验环境和试样尺寸效应等因素的影响，加上岩土体自身复杂的结构性和力学性质的空间变异性，通过室内和现场试验获得的力学参数通常与岩土体实际参数有较大偏差，而通过工程类比得到的经验参数则更显粗略。因此，充分利用现场监测得到的岩土体位移信息，借助一定的力学模型和数值计算方法，反推出岩土体力学参数的反分析方法逐渐发展成为解决岩土体计算参数取值问题的主要途径，并且在实际工程中得到了广泛应用[1-8]。但是，在利用反分析方法确定岩土体参数时，计算量通常相当大[9]，如果能够识别出影响岩土体变形的主要参数，进而有针对性地进行参数反演，将大大减小工作量，提高反分析的准确性和效率[10]。

敏感性分析是一种系统分析方法，该方法假设系统的某个特性K由n个影响因子决定，即K=f(x1,x2,…,xn)。令每个因子在偏离基准值的一定范围内变动，若xi的较小变化就能引起K的较大变化，则表明K对xi敏感，xi即可判定为系统特性K的高敏感性参数，反之亦然[11]。因此，敏感性分析成为解决岩土工程多参数辨识问题的主要方法。目前，文献记载的因素敏感性分析方法主要有非参数统计方法[12]、曲线斜率法[13-14]、敏感性系数法[15]、敏感度函数法[10,16-17]、正交试验法[18-22]、均匀设计法[23]、灰色关联度分析法[24-25]、人工神经网络[26-27]等，其中以敏感性系数法、敏感度函数法和正交试验法这3种方法应用最为广泛。前2种方法虽然简单易行，但是对于多参数的敏感性分析问题存在多解性，排序结果会受到参数水平和拟合函数的影响，只适用于参数较少的情况[22]。另一方面，岩土体力学参数之间存在固有的相关性，它们对系统的影响是相互交叉、综合作用的，因而传统单因素条件下的分析方法显得不尽合理[12,19]。研究表明，正交试验法的设计规则科学合理，不仅能够最大限度地减少试验次数，而且统计分析结果还可以判定影响因素的显著性水平，可对因素的敏感程度进行量化考核，因此，正交试验法对于多因素敏感性分析问题更加适用[18-22]。

本文以重庆万州驸马长江大桥北岸重力锚基坑作为研究对象，采用正交试验法对影响基坑开挖变形的岩土体力学参数进行敏感性分析，试图辨识出影响基坑变形的主要因素，从而为后续开展的位移反分析工作奠定基础，以及为控制基坑开挖变形提供施工指导建议。

2 正交试验法及统计分析原理

2.1 正交试验法原理介绍

正交试验法[28-29]是研究多因素多水平的一种试验设计方法，根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些代表性的点具有“均匀分散、整齐可比”的特征。正交试验法在水平较少的情况下具有较高的效率，可以快速找出各相关因素对基坑变形的影响程度。正交表是正交试验设计的基本工具，通常记为Ln(tm)，其中L为表符号，t为因素水平数，m为因素个数，n为试验次数。正交表具有2项重要性质：①每一列中，不同的数字出现的次数相等；②任意2列中数字的排列方式齐全且均衡。通俗地说，每个因素的每个水平与另一因素的各个水平各结合一次，即为正交性。

2.2 正交试验结果的统计分析方法

对正交试验结果的分析，通常采用2种方法[18,30]：一种是极差分析法，也称为直观分析法；另一种是方差分析法。

极差分析法中，先求出各因素在每一水平下试验指标的平均值，然后计算同一因素不同水平下试验指标均值的极差，极差越大，说明该因素的水平改变时对试验结果的影响越大，可判定为主要因素，反之亦然。以下标i表示因素水平号，下标j表示不同因素的编号，那么因素j的极差Rj的计算公式为

(1)

式中Kij为因素j水平号为i的各试验结果之和。

极差分析法的优点是简单、直观，计算量较小，缺点是不够精确。采用方差分析可以弥补极差分析的不足。方差分析法是将数据的总离差平方和分解为因素的离差平方和与误差平方和之和，利用各因素的离差平方和与误差平方和构造检验统计量，作给定显著性水平α的F检验，每个因素的F值或概率P值的大小顺序即反映了试验指标对该因素的敏感程度。

假设采用正交表Ln(tm)安排试验，试验结果为y1,y2,…,yn，那么数据的总离差平方和QT为

(2)

其中:

(3)

(4)

因素j引起的数据的离差平方和Qj为

(5)

式中：Tij为正交表Ln(tm) 第j列第i水平的计算结果yi之和；r为各因素每一水平的试验次数，且

(6)

QT和Qj的自由度分别为：

fT=n-1 ;

(7)

fj=t-1 。

(8)

将所有空白列的离差平方和相加，记为Qe；对应的自由度相加，记为fe，构造统计量Fj，即

(9)

对于给定的显著性水平α，当Fj>F1-α(fj,fe)时，即可判定该因素在检验水平α下影响显著。

3 重力锚基坑工程概况

以重庆万州驸马长江大桥北岸重力式锚碇基坑作为研究对象，该基坑是全桥的控制性工程。基坑基底尺寸为73 m×48 m(长×宽)，最大开挖深度38.5 m。在基坑周围共设置78根桩径1.5 m的钢筋混凝土防护桩，桩长在12.015～18.500 m之间，桩顶设置帽梁连接。在防护桩上部设置1～4层预应力锚索，长度为16～35 m，设计预应力600 kN。基坑西北角外侧设置10根截面尺寸为2.5 m×1.8 m(长×宽)的抗滑桩，桩长为12.5～15.0 m。

根据施工设计方案，重力锚基坑采取分层开挖的方式，1～5层采取垂直向下开挖，前4层开挖后立即施作锚索；6～13层采取水平方向开挖，设计开挖总层数为13层。基坑支护结构设计和开挖步骤如图1所示。基坑开挖施工的数值模拟步骤见表1。

重力锚基坑三维计算模型范围为：宽202 m(x方向)，长235 m(y方向)，模型底面标高170 m。x轴正向垂直于基坑轴线、指向长江下游侧；y轴正向平行于基坑轴线、指向长江北侧岸坡；z轴正向垂直于xy平面指向竖直向上。模型共划分1 036 654个单元，431 583个节点。基坑三维计算模型和支护结构模型见图2和图3。

图1 基坑支护结构和开挖步骤示意图

表1 重力锚基坑开挖施工数值模拟步骤

(a)整体模型 (b)局部模型

注：1.全风化层; 2.强风化砂质泥岩; 3.中风化砂质泥岩; 4.重力锚基坑

图2重力锚基坑三维计算模型

Fig.2Three-dimensionalcomputationalmodelofthegravityanchorexcavation

模型地层概化为3种材料，自上而下依次为：第四系残坡积及崩坡积粉质黏土混碎块石(全风化层)、强风化砂质泥岩(强风化层)、以及中风化砂质泥岩(中风化层)。岩土体均采用弹塑性本构模型、Mohr-Coulomb屈服准则；防护桩、帽梁、抗滑桩均采用弹性模型；预应力锚索采用FLAC3D内置的cable单元进行模拟。岩土体主要物理力学参数见表2。模型各侧面分别设置相应的法向位移约束，底部设置竖向位移约束，上部边界为自由边界。

图3重力锚基坑支护结构模型

Fig.3Supportingstructureofgravityanchorexcavation

注：1.抗滑桩; 2.帽梁; 3.防护桩; 4.预应力锚索

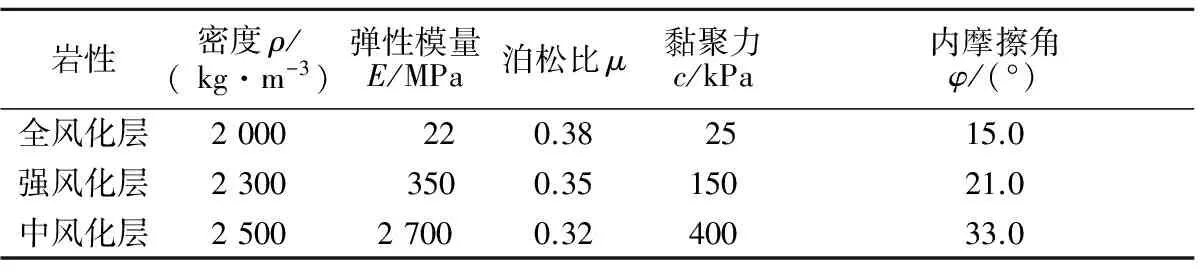
表2 重力锚基坑岩土力学参数基准值

4 岩土参数敏感性分析

4.1 正交试验设计方案及计算结果

根据正交试验设计原理，结合重力锚基坑地层岩性特征和支护结构受力特征，选取基坑中轴线上的41#防护桩顶水平位移(垂直于基坑方向)作为试验指标；以影响基坑开挖变形的主要力学参数，即将3种地层材料的弹性模量E、泊松比μ、黏聚力c以及内摩擦角φ作为影响因素，共涉及12个力学参数，同时将每个参数划分为3个水平，因素及因素水平取值见表3。采用13因素3水平正交表L27(313)进行试验方案的设计，除了12个力学参数以外，将正交表第13列作为试验误差项。在本文中，将重力锚基坑的一次开挖变形计算看作一次“试验”，采用有限差分软件FLAC3D进行基坑开挖变形计算，共进行27次数值计算。基于正交试验设计的计算方案及数值计算结果见表3。

4.2 计算结果统计分析

表3 基于正交试验设计的数值计算方案及结果

注：括号内的数值是因素在该水平下的取值;E1,E2,E3单位均为MPa;c1,c2,c3单位均为kPa;φ1,φ2,φ3单位均为(°)

表4 正交试验结果极差分析

注：SUM(i) (i=1, 2, 3)为该因素取水平i时的桩顶位移之和；AVE(i)(i=1, 2, 3)为9次试验位移之和SUM(i)的平均值；R为均值AVE(i)的极差

表4为正交试验结果的极差分析，可以看出，全风化层的弹性模量E1、泊松比μ1、黏聚力c1、内摩擦角φ1以及强风化层的弹性模量E2这5个参数的极差相对较大，表明基坑变形对于上述5个参数较为敏感，各参数敏感性主次顺序为E1→E2→φ1→c1→μ1→c2→μ2→φ2→E3→c3→φ3→μ3。其中E1对基坑变形影响最大；剩余7个参数对应的位移极差均<1 mm，表明基坑变形对于剩余7个参数不太敏感。

从不同参数水平下桩顶水平位移均值的变化趋势(图4)可以看出，上述5个参数指标变化幅度较大，而剩余7个参数指标变化趋势较为平缓，同样反映了上述5个参数对基坑变形影响较大。

图4不同参数水平下桩顶水平位移变化趋势

Fig.4Trendofhorizontaldisplacementoftheretainingpiletopwithdifferentlevelsofrock-soilparameters

在极差分析的基础上，为了进一步检验各影响因素的显著性水平，对试验结果进行方差分析。利用式(5)计算出各因素列的离差平方和Qj。根据式(8)，本文各因素列自由度fj=2，误差列自由度fe=2,选取显著性水平α=0.01，0.05，查F分布分位数表可知：F0.99(2,2)=99.00，F0.95(2,2)=19.99。定义:当Fj>F0.99(2,2)时，因素高度显著，记为“**”；当F0.95(2,2)≤Fj≤F0.99(2,2)时，因素显著，记为“*”；当Fj

表5 正交试验结果方差分析

方差分析结果显示：全风化层的弹性模量E1、泊松比μ1、黏聚力c1、内摩擦角φ1以及强风化层的弹性模量E2这5个参数对基坑变形的影响程度为显著，其中E1，c1，φ1，E2这4个参数的影响程度为高度显著，而剩余的7个参数对基坑变形的影响并不显著。根据表5显示的统计量F值和概率P值大小，各参数的敏感性由大到小排序为：E1→E2→φ1→c1→μ1→c2→μ2→φ2→E3→c3→φ3→μ3。由此可见，方差分析结果和前述极差分析结果完全一致，反映了正交试验法的科学性和敏感性分析结果的正确性。

5 结果分析与讨论

(1)本文的研究对象重力锚基坑涉及的岩土体参数众多，属于典型的多因素敏感性分析问题。基于正交试验设计的计算方案最大限度地减少了计算工作量，全面反映了众多参数对基坑变形的综合影响作用。极差分析和方差分析显示的参数敏感性顺序完全一致，证实了正交试验法对于岩土工程多参数辨识问题的适用性和有效性。

(2)极差分析和方差分析均显示，全风化层的弹性模量E1、泊松比μ1、黏聚力c1、内摩擦角φ1以及强风化层的弹性模量E2这5个参数对基坑变形影响相对较大。现场地质调查显示，地表全风化层为松散土体，强风化层为破碎岩体，中风化层为层状块体结构的岩体，全、强风化层的力学性质明显相对较差，因而在开挖卸荷作用下必然产生更大的变形，即基坑变形对于全、强风化层参数更加敏感。因此，地质定性分析在一定程度上也证实了敏感性分析结果的正确性。

(3)本文的敏感性分析结果对于后续的参数反演具有一定的指示意义。基坑开挖变形计算结果显示，基坑变形总体较小，防护桩最大水平位移<25 mm，并且模型中不存在贯通的塑性区域。由此推断重力锚基坑在开挖条件下，岩土体仍以弹性变形为主，反演强度参数c1和φ1意义并不大;而泊松比μ与其他参数相比，重要性低一些，建议采用设计值[31]。因此，根据敏感性分析结果，建议反演目标参数为全、强风化层的弹性模量E1和E2。

(4)敏感性分析结果对于控制基坑开挖变形也具有一定的施工指导意义。根据施工设计方案，重力锚基坑开挖前4层时，涉及的地层为全、强风化层，而敏感性分析结果显示，基坑变形对于全、强风化层的变形参数最为敏感。因此，在实际施工过程中，应严格按照设计深度和范围进行开挖，1—4层开挖完成后应立即施作预应力锚索，结合现场变形及应力监测数据，待岩土体变形稳定后再进行下一层开挖，防止基坑在开挖前期由于变形过大而发生坍塌事故。

(5)影响基坑变形的因素通常包含基坑岩土体参数和支护结构设计参数2个方面[32]，由于本文的研究目的主要是为后续开展的位移反分析确定反演目标参数，因而并未论述支护结构参数对于基坑变形的影响，关于后者的研究笔者将另文专述。

6 结 论

以重庆万州驸马长江大桥北岸重力锚基坑作为研究对象，采用正交试验法对影响基坑变形的岩土体参数进行了敏感性分析，主要得到以下结论：

(1)正交试验法的设计规则科学合理，避免了传统单因素分析方法的不足，全面反映了各因素对系统的综合影响作用，统计分析提供了判断因素敏感程度的量化标准，该方法适用于岩土工程多参数敏感性分析。

(2)极差分析和方差分析均显示E1，μ1，c1，φ1，E2这5个参数对基坑变形的影响显著，方差分析显示E1，c1，φ1，E2这4个参数的影响程度为高度显著，而剩余7个参数的影响并不显著。结合重力锚基坑开挖试算结果，最后综合确定的反演目标参数为全、强风化层的弹性模量E1和E2。

(3)在实际施工过程中，应严格按照设计方案进行基坑开挖，充分利用现场监测数据分析岩土体变形情况和支护结构受力情况，避免基坑在开挖前期由于变形过大而发生坍塌事故。

[1] SAKURAI S, TAKEUCHI K. Back Analysis of Measured Displacements of Tunnels[J]. Rock Mechanics and Rock Engineering, 1983, 16(3): 173-180.

[2] FENG X T, ZHANG Z, SHENG Q. Estimating Mechanical Rock Mass Parameters Relating to the Three Gorges Project Permanent Shiplock Using an Intelligent Displacement Back Analysis Method[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(7): 1039-1054.

[3] DENG J H, LEE C F. Displacement Back Analysis for a Steep Slope at the Three Gorges Project Site[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(2): 259-268.

[4] YANG Zhi-fa, WANG Zhi-yin, ZHANG Lu-qing,etal. Back-Analysis of Viscoelastic Displacements in a Soft Rock Road Tunnel[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 331-341.

[5] MAJDI A, BEIKI M. Evolving Neural Network Using a Genetic Algorithm for Predicting the Deformation Modulus of Rock Masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2):246-253.

[6] 朱泽奇, 盛 谦, 张勇慧, 等. 龙滩水电站左岸进水口边坡三维位移反分析[J]. 长江科学院院报, 2008, 25(2):33-37.

[7] 董志宏, 丁秀丽, 卢 波, 等. 大型地下洞室考虑开挖卸荷效应的位移反分析[J]. 岩土力学, 2008, 29(6): 1562-1568.

[8] 李守巨, 刘迎曦, 孙 伟. 智能计算与参数反演[M]. 北京: 科学出版社, 2008.

[9] 邓建辉, 李焯芬, 葛修润. BP网络和遗传算法在岩石边坡位移反分析中的应用[J]. 岩石力学与工程学报, 2001, 20(1):1-5.

[10] 杨 蒙, 谭跃虎, 李二兵, 等. 基于敏感性分析的围岩力学参数反演方法研究[J]. 地下空间与工程学报, 2014, 10(5):1030-1038.

[11] 黄书岭, 冯夏庭, 张传庆. 岩体力学参数的敏感性综合评价分析方法研究[J]. 岩石力学与工程学报, 2008, 27(增1):2624-2630.

[12] 贾善坡, 陈卫忠, 李香玲. 基于非参数统计的泥岩水-力耦合参数敏感性分析[J]. 地下空间与工程学报, 2008, 4(5):830-834.

[13] SHAKOOR A, SMITHMYER A J. An Analysis of Storm-Induced Landslides in Colluvial Soils Overlying Mudrock Sequences, Southeastern Ohio, USA[J]. Engineering Geology, 2005, 78(3): 257-274.

[14] 石豫川, 冯文凯, 刘汉超, 等. 特大多期复合型滑坡稳定性评价及因素敏感性分析[J]. 岩土力学, 2004, 25(6):975-980.

[15] 文宝萍, 申 健, 谭建民. 水在千将坪滑坡中的作用机理[J]. 水文地质工程地质, 2008, 35(3):12-18.

[16] 章 光, 朱维申. 参数敏感性分析与试验方案优化[J]. 岩土力学, 1993, 14(1):51-58.

[17] 王 辉, 陈卫忠. 嘎隆拉隧道围岩力学参数对变形的敏感性分析[J]. 岩土工程学报, 2012, 34(8):1548-1553.

[18] 倪 恒, 刘佑荣, 龙治国. 正交设计在滑坡敏感性分析中的应用[J].岩石力学与工程学报,2002, 21(7)：989-992.

[19] 葛 华, 刘汉超. 万州草街子双堰塘滑坡稳定性影响因素敏感性分析[J]. 中国地质灾害与防治学报, 2003, 14(2):15-18.

[20] 徐 超, 叶观宝. 应用正交试验设计进行数值模型参数的敏感性分析[J]. 水文地质工程地质, 2004, 31(1):95-97.

[21] 刘长春, 殷坤龙, 李远耀. 巴东县文家滑坡稳定性计算及其敏感性分析[J]. 水文地质工程地质, 2010, 37(1):113-117.

[22] 蒋 树, 文宝萍. 基于不同方法的滑坡滑带力学参数敏感性分析[J]. 工程地质学报, 2015, 23(6):1153-1159.

[23] 陈高峰, 程圣国, 卢应发, 等. 基于均匀设计的边坡稳定性敏感性分析[J]. 水利学报, 2007, 38(11):1397-1401.

[24] 付建军, 邱山鸣, 赵海斌, 等. 基于灰色关联度的边坡稳定影响因素分析[J]. 长江科学院院报, 2011, 28(1):53-57.

[25] 赵永虎, 刘 高, 毛 举, 等. 基于灰色关联度的黄土边坡稳定性因素敏感性分析[J]. 长江科学院院报, 2015, 32(7):94-98.

[26] 夏元友, 熊海丰. 边坡稳定性影响因素敏感性人工神经网络分析[J]. 岩石力学与工程学报, 2004, 23(16):2703-2707.

[27] 赵启林, 吉 林. 参数灵敏度分析的有限元-神经网络混合法[J]. 土木工程学报, 2004, 37(4):60-63.

[28] 马良驹, 袁灿勤. 岩土工程勘察数据统计分析[M]. 南京: 南京大学出版社, 1991.

[29] 方开泰, 马长兴. 正交与均匀试验设计[M]. 北京: 科学出版社, 2001.

[30] 吴 翊,李永乐，胡庆军. 应用数理统计[M]. 长沙: 国防科技大学出版社, 1997.

[31] 陈胜宏, 陈尚法, 杨启贵. 三峡工程船闸边坡的反馈分析[J]. 岩石力学与工程学报, 2001, 20(5):619-626.

[32] 张维正, 郝 哲, 肖明儒. 深基坑开挖及支护工程理论与实践[M]. 北京:人民交通出版社, 2014.

Sensitivity Analysis of Rock-Soil Parameters of a Gravity Anchor Excavation Based on Orthogonal Experiment Method

RAN Tao1，MAO Jiang-nan2， MEI Song-hua3，WANG Wei-wei4，TAN Li-hua4

(1.Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China； 2.Engineering Quality and Safety Supervision Bureau of Chongqing Traffic Committee, Chongqing 400060, China；3.Zhongnan Engineering Co. Ltd., Power China, Changsha 410014, China；4.First Division of Fuma Yangtze River Bridge, China First Highway Engineering Co. Ltd., Wanzhou 404000, China)

In the aim of investigating the sensitivity of rock-soil parameters during the deformation of gravity anchor excavation, FLAC3Dwas employed to simulate the deformation based on orthogonal experiment design, and range analysis and variance analysis were conducted for the simulation results. The gravity anchor excavation of Fuma Yangtze River Brideg in Wanzhou District, Chongqing City, was selected as the research object. Results of range analysis and variance analysis both suggest that elastic modulusE1, poisson’s ratioμ1, cohesionc1, and internal friction angleφ1of completely-weathered layer and elastic modulusE2of strongly-weathered sandy mudstone were identified as the dominant geotechnical parameters that affect the deformation of excavation. Furthermore in association with trial calculation results,E1andE2were determined as the target parameters of inversion analysis. The research results laid a foundation for subsequent displacement back analysis, provided guiding suggestion for controlling the deformation of excavation, and offered a reference for sensitivity analysis of similar engineering as well.

deep excavation project; sensitivity analysis; rock-soil parameters; orthogonal experiment method; statistical analysis

10.11988/ckyyb.20160804

2016-08-10；

2016-09-23

冉 涛(1985-)，男，四川广元人，博士研究生，主要从事工程地质和岩土工程方面的研究。E-mail:rantaopaul@aliyun.com

TU441.3

A

1001-5485(2018)01-0101-06

(编辑：占学军)