导数在函数解题中的几点应用

顾准山

（江苏省镇江市第四中学，江苏镇江 212000）

导数在函数解题中的几点应用

顾准山

（江苏省镇江市第四中学，江苏镇江 212000）

函数作为高中数学的主要知识点，始终是高考的重点与热点，而导数作为解决函数问题的重要工具，其重要性不言而喻。本文对导数知识进行了综合梳理，对运用导数知识解决函数问题进行了分类总结，对提升学生分析问题、解决问题的能力有较好的指导作用。

导数；函数；应用

引 言

现行高中数学教材中，导数作为解决数学问题强有力的工具，是初、高等数学知识的重要衔接点，渗透和加强了对学生从有限到无限、从量变到质变的辩证思想的教育，突破了许多初等数学在思想上的桎梏，拓宽、优化和丰富了许多数学问题解决的思路、方法和技巧[1]；另一方面，导数具有很强的知识交汇能力，与多个章节内容都联系紧密，尤其是函数部分，由于函数是高考的重点和热点之一，而导数是研究函数的重要工具，所以导数的地位正在不断加强，对导数应用考查的广度和深度也在不断加重。

一、导数的物理意义和几何意义

导数的物理意义：如函数s=s（t）在t0处的导数s'（t0），就是物体在时刻t0时的瞬时速度v，即v=s'（t0）；函数v=v（t）在t0处的导数v'（t0），就是物体在时刻t0时的瞬时加速度a，即a= v'（t0）；降雨强度是降雨量关于时间的导数等。

导数的几何意义：曲线y=f（x）在x0处的导数f '（x0），就是曲线在x0处的切线的斜率k，即k=f '（x0）。

例1：在抛物线y=x2上存在一点P，使得点P到直线2x-y-4=0的距离最短，则点的坐标是 （1,1）

二、导数在研究函数中的应用

1.求曲线在（过）某点的切线方程

例2：求曲线y=x3-3x过点P（2，2）的切线方程。（y=0或y=9x-16）

分析：即使点（2，2）恰好在曲线上，由于是求“过”（而不是“在”）点P处的切线方程，仍然要考虑两种情况，一是点P就是切点，二是点P不是切点，可以设出切点坐标，利用切线斜率的两种表示方法解出切点坐标，从而解决问题。

2.解决函数单调性有关的问题

导数与函数的单调性的关系：①f '(x)＞0是f (x)为增函数的充分不必要条件；②f '(x)≥0是f (x)为增函数的必要不充分条件。因此f (x)在某区间上递增在该区间上恒成立，f (x)在某区间上为递减在该区间上恒成立。值得注意的是，求函数的单调区间一定要先求函数的定义域。

3.求函数的极值与在闭区间上的值域

求函数极值点的一般步骤：先求导，令导数为零，再根据导函数判断零点两边的单调性，得出函数的极值点。

注意：导数为0的点（称为驻点），不一定是极值点；但在导函数存在的前提下，极值点的导数值必为0。

例3：已知函数f（x）=x3+ax2+bx+a2在x=1处取得极值10，求a+b的值。

求函数值域的一般步骤：求出函数在闭区间上的极值，再与区间端点比较大小即可。

例 4：已知函数 f（x）=x3+ax2+bx+c，过曲线 y=f（x）上的某点P（1，f（1））的切线方程为y=3x+1；

（1）设函数f（x）在x=-2处有极值，求出f（x）的表达式；（f（x）=x3+2x2-4x+5）

（2）在（1）的条件下，求出f （x）在[-3，1]上的最大值；（f（x）max=f（-2）=13）

（3）若函数y=f（x）在区间[-2，1]上单调递增，求出b的取值范围。（b≥0）

分析（3）：函数y=f（x）在区间[-2，1]上单调递增，所以f ' （x）≥0在该区间上恒成立，然后分离变量，转化为函数的最值问题求解。

4.利用导数证明不等式

基本原理：欲证不等式f（x）＞g（x），构建函数h（x）=f（x）-g（x），只要求出函数h（x）的最小值，证明此最小值大于0即可。

例5：设函数f（x）=x2ex-1+ax3+bx2，已知x=-2和x=1为f（x）的极值点。

（Ⅰ）求a和b的值；（Ⅱ）讨论f（x）的单调性；

解：（Ⅰ）因为f ' (x)=ex-1(2x+x2)+3ax2+2bx=xex-1(x+2)+x(3ax+2b)，又x=-2和x=1为f（x）的极值点，所以f ' (-2)=f '(1)=0，

因为x∈[1,+∞)时，h' (x)≥0，所以h(x)在x∈(1,+∞)上单调递增。

故x∈[1,+∞)时，h(x)≥h(1)=0。所以对任意x∈[-∞ ,+ ∞ )，恒有 h(x)≥ 0，又 x2≥ 0，因此 f（x）-g（x）≥0，故对任意x∈（-∞,+∞)，恒有f（x）≥g（x）。

5.利用导数求方程根的个数

一般步骤：求出对应函数的单调性，求出极值，做出草图，即可解决。

例 6： 已 知 函 数 f（x）=x+a，g(x)=x2+3x+2，F(x)=f（x）·g(x)，①若F(x)在(-1，1)上为减函数,求a的取值范围；②若y=f (x)的图像与y=g(x)的图像相切，试讨论关于x的方程F(x)=k (k∈R)的实根个数。（当或k＜0时，有一个实根；当或k=0时，有两个实根；当时有三个实根）

6.优化实际问题

例7：水库的蓄水量随时间而变化，现用t表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于t的近似函数关系式为

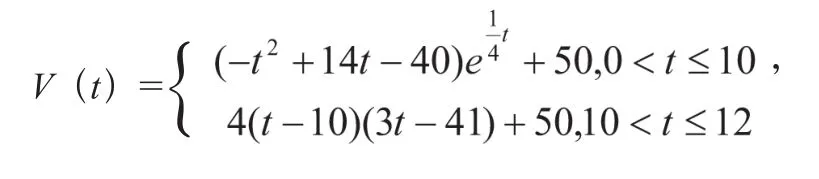
（Ⅰ）该水库的蓄水量小于50的时期称为枯水期，以i－1＜t＜i表示第i月份（i=1,2,…,12），问一年内哪几个月份是枯水期？

（Ⅱ）求一年内该水库的最大蓄水量（取e=2.7计算）。（08湖北）

②当10＜t≤12时，V（t）＝4（t－10）（3t－41）+50＜50，

综合得0＜t＜4,或10＜t≤12，

故知枯水期为1月，2月，3月，4月，11月，12月共6个月。

(Ⅱ)由(Ⅰ)知：V（t）的最大值只能在（4，10）内达到。

令V′(t)=0，解得t=8(t=－2舍去)。

当t变化时，V′(t) 与V (t)的变化情况如下表：

(4,8) 8 (8,10)V′(t) + 0 －V(t) 极大值t

由上表，V(t)在t＝8时取得最大值V(8)＝8e2+50≈108.32(亿立方米)。

故知一年内该水库的最大蓄水量是108.32亿立方米。

结 语

物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。导数物理意义和几何意义明确，在研究函数中的应用可以体现在以上求曲线在（过）某点的切线方程，解决函数单调性有关的问题，求函数的极值与在闭区间上的值域，利用导数证明不等式，优化实际问题等方面[2]。通过综合梳理、分类总结导数在函数解题中的应用，希望对提升学生分析问题、解决问题的能力有较好的指导作用。

[1]邹生书.函数极值点偏移问题的三种求解策略[J].中学数学教学,2017,(03):42-44.

[2]夏峰,邓慧.导函数零点问题的转化求解[J].高中数理化,2017,(Z1):19.

顾准山（1973），男，江苏镇江人，本科学历，中学数学高级教师。