山区220kV输电线路绕击跳闸率的计算

贾 茹，王 超，鲁志伟，高嘉义，李 博，李 旭

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网通化供电公司，吉林 通化 134000；3.天津力神动力电池系统有限公司，天津 300384)

山区220kV输电线路绕击跳闸率的计算

贾 茹1，王 超2，鲁志伟1，高嘉义3，李 博1，李 旭1

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网通化供电公司，吉林 通化 134000；3.天津力神动力电池系统有限公司，天津 300384)

山区地面起伏比较大，造成雷电多发，大大增加了输电线路雷击的概率。雷电绕击受地形的影响比较严重，使得山区绕击跳闸率的计算比较困难。为此需要对地形进行一些近似，将山区地形分为4种，分别为山顶、沿坡、爬坡和跨谷。在各类地形的前提条件下利用电气几何模型对山区输电线路绕击跳闸率进行推导和计算，特别是对跨谷地形进行了合理近似，量化了该地形下输电线路的绕击跳闸率，证明了跨谷地形的绕击风险相对比较高。以通化地区220 kV输电线路为例，通过故障实例的计算和分析，验证了该绕击计算方法的正确性和可靠性，并比较了输电线路所处地面倾角和地形对其绕击跳闸率的影响。

山区；复杂地形；绕击跳闸率；地面倾角

山区的高压架空输电线路由雷击造成的跳闸事故占输电线路故障的大部分。输电线路雷击跳闸率计算的准确程度对保证电网安全可靠运行和差异化防雷改造具有重要意义。目前输电线路绕击跳闸率的计算方法主要有先导发展模型和电气几何模型。先导发展模型更贴近雷电发展的物理机制，但需要进一步考虑空间电荷分布、先导发展速度、先导发展随机性和先导通道的互相影响；电气几何模型将雷电放电特性和线路结构尺寸联系在一起，对于220 kV及以下的输电线路，采用该模型进行绕击分析的可信度较高[1]。暴露距离可以反应地面倾角等地形参数，故本文将利用电气几何模型中的暴露距离法进行绕击跳闸率计算[2-4]。地面倾角是衡量地形的一个重要指标，它对绕击跳闸率的影响很大，为此将根据计算结果对其影响程度进行分析。

1 绕击计算模型

1.1 绕击耐雷水平

《国标》中的绕击耐雷水平Imin为[5]：

(1)

式中：U-50%为绝缘子负极性50%闪络电压绝对值；Z0为闪电通道波阻，取Z0=300 Ω；Zc为导线波阻抗，取Zc=900 Ω；Uph为导线上工作电压瞬时值，对于220 kV的输电线路的影响不大，故本文将其忽略。

1.2 击距公式

根据经典EGM，击距的大小与先导头部的电位有关，因而与先导通道的电荷密度有关。后者又决定了随后出现的雷电流幅值，所以认为击距是雷电流幅值的函数[6]。计算公式为

rs=rc=10I0.65，

(2)

(3)

式中：rs为雷电对地线的击距；I为雷电流幅值；rc为雷电对导线的击距；rg为雷电对大地的击距；hc为导线对地平均高度。击距系数β为

(4)

1.3 绕击跳闸率的计算

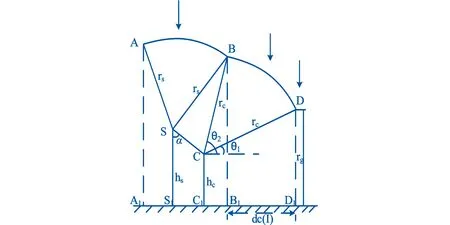
图1 电气几何模型示意图

本文运用的电气几何模型计算绕击跳闸率，如图1所示。避雷线的悬挂点为S、导线的悬挂点为C，hs为避雷线的平均高度，θ1为线段CD与地面的夹角，θ2为线段CB与地面的夹角，α为避雷线的保护角。

暴露距离为dc(I)，最大绕击雷电流为Imax，雷电流概率密度函数为f(I)，建弧率为η，落雷密度为Ng，档距长度为L，得到绕击跳闸率SFTR为[7]

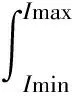
(5)

式中：

dc(I)=rc(cosθ1-cosθ2)，

(6)

(7)

(8)

设θ为地面倾角，最大绕击雷电流Imax的计算可以根据最大击距Rmax来求解，Rmax的通用公式如下[8]：

(9)

其中：

F=β2-sin2(α+θ)，

(10)

G=F[(hs-hc)/cosαcosθ]2.

(11)

由最大击距求最大绕击雷电流Imax：

Imax=(0.1×Rmax)1.54.

(12)

2 复杂地形绕击跳闸率分析

山区地形复杂多变，输电线路的雷击跳闸事故多发，所处地形对绕击跳闸有很大的影响，故将山区分成4种典型地形，分别为山顶、沿坡、爬坡和跨谷[9-10]。因此，本文将主要从这四种情况进行分析。

2.1 输电线路位于山顶

双避雷线输电线路的电气几何模型，如图2所示。山体的左、右侧倾角分别为θL和θR，输电线路左、右侧暴露距离分别为dCL和dCR，ImaxL和ImaxR分别为输电线路左右侧的最大绕击雷电流，输电线路的左侧、右侧和总体绕击跳闸率的计算公式如下：

图2 输电线路位于山顶时的电气几何模型示意图

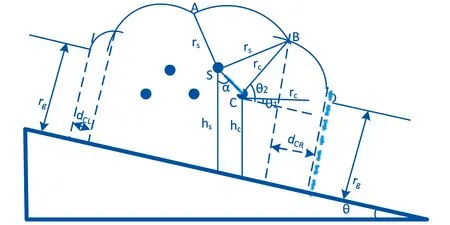
图3 输电线路沿坡时的电气几何模型示意图

(13)

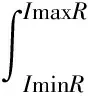
(14)

SFTR=SFL+SFR，

(15)

式中：

dCL(I)=dCR(I)=rc(cosθ1-cosθ2)，

(16)

(17)

(18)

因此，左侧的θ1、θ2与右侧的计算类似。

计算左、右两侧最大击距可根据公式(9)。计算左侧时，取地面倾角θ=θL；计算右侧时，取地面倾角θ=θR。根据公式(12)计算两侧的最大绕击雷电流。

2.2 输电线路沿坡

双避雷输电线路的电气几何模型如图3所示，山坡的倾角为θ，输电线路的走向为沿着山坡，从图3中可以看出左侧的暴露距离dCL比右侧暴露距离dCR小，左侧的绕击跳闸率比右侧的小。输电线路的左侧、右侧和总体绕击跳闸率计算公式同式公式(13)、公式(14)和公式(15)，dCL和dCR的计算如下：

dCL(I)=dCR(I)=rc(cosθ1-cosθ2)，

(19)

其中：左、右两侧θ1的计算公式相同，而θ2的计算公式不同。左侧的地面倾角θL=-θ，右侧的地面倾角θR=θ。θ1、左侧θ2L、右侧θ2R的计算公式如下：

(20)

(21)

(22)

因此，最大绕击雷电流的计算与山顶情况的一致。

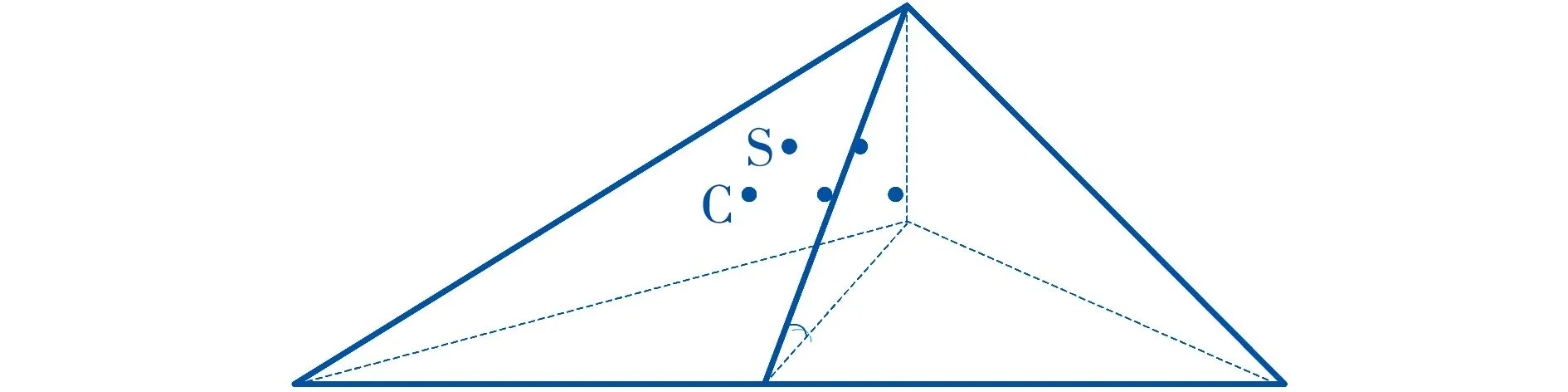
图4 输电线路爬坡时的电气几何模型示意图

2.3 输电线路爬坡

双避雷输电线路的电气几何模型如图4所示，如果山坡平整，那么垂直于线路走向的地面倾角为0。输电线路的左侧和右侧的绕击跳闸率相等，故总体绕击跳闸率计算公式如下：

(23)

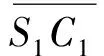
(24)

此时地面击距rg的计算公式为

(25)

输电线路的暴露距离由公式(6)计算，此时θ1、θ2的计算公式为：

(26)

(27)

此时的最大击距为

(28)

其中：

(29)

G=F[(hs-hc)cosθ/cosα]2.

(30)

图5 输电线路跨谷时的导地线对地高度示意图

2.4 输电线路跨谷

大多数输电线路跨谷是一个大档距，随着档距的增加，杆塔绕击跳闸率会继续增加[11-13]。跨谷相当于两个爬坡地形，一个在谷底左侧，一个在谷底右侧，但是与爬坡不同的地方是导地线对地高度在同一个山坡上变化比较快，平均高度要比爬坡高，所以要对平均高度进行修正[14]。这种情况下双避雷输电线路的导地线对地高度如图5所示，N点为谷底，弧AB为导线或地线，由MN分成左右两部分进行计算推导。

谷底左侧输电线路或避雷线平均高度hL和右侧平均高度hR如下：

(31)

(32)

其中：

(33)

(34)

式中：T为导线张力；g=9.8 N/m；f为导线弧垂，m。

根据爬坡公式(23)-公式(30)分别计算谷底左侧和谷底右侧的绕击跳闸率SFL和SFR，最后由公式(35)计算得总的绕击跳闸率

(35)

3 算例分析

以通化地区220 kV输电线路长郑79#杆塔为例，研究了在不同地形情况下，地面倾角对绕击跳闸率的影响。该基杆塔类型为直线塔ZM2，塔高27.5 m，呼称高21 m，档距为467 m。根据杆塔结构图，计算避雷线平均高度hc为17.5 m，导线平均高度hs为13.3 m，保护角α为11.3°，导地线间的距离为12.8 m。

(1)输电线路位于山顶

当输电线路位于山顶时，假设两侧地面倾角相等，计算得其绕击跳闸率与地面倾角的关系如图6所示，可以看出绕击跳闸率随着地面倾角的增大而增大，而且增大趋势比较迅速。当地面倾角在0°～40°变化时，绕击跳闸率从0.223 7次/百公里·年上升到3.851 7次/百公里·年。

(2)输电线路沿坡

当该杆塔处于沿坡，计算绕击跳闸率与地面倾角的关系如图7所示，可以看出随着地面倾角的增大，杆塔的绕击跳闸率增大，而且增大趋势比较缓慢。当地面倾角在0°～40°变化时，绕击跳闸率从0.223 7次/百公里·年上升到2.188 6次/百公里·年。

(3)输电线路爬坡

当该杆塔位于爬坡情况，此时的地面倾角取沿着线路走向，即山坡的角度，计算绕击跳闸率与地面倾角的关系如图8，可以看出随着地面倾角的增大，杆塔绕击跳闸率在逐渐减小。当地面倾角在0°～40°变化时，绕击跳闸率从0.223 7次/百公里·年下降到0.027 5次/百公里·年。

图6 山顶绕击跳闸率随地面倾角的变化情况图7 沿坡绕击跳闸率随地面倾角的变化情况图8 爬坡绕击跳闸率随地面倾角的变化情况图9 跨谷绕击跳闸率随地面倾角的变化情况

(4)输电线路跨谷

当该杆塔位于跨谷情况，假设谷底左右的地面倾角相等，谷底位于档距中央，随着地面倾角的增大，山谷的深度也在增大，其绕击跳闸率与地面倾角的关系如图9，可以看出随着地面倾角的增大其绕击跳闸率在增大，并且增长迅速，在地面倾角在0°～40°变化时，绕击跳闸率从0.223 7次/百公里·年上升到4.485 1次/百公里·年。

表1 220 kV长郑线地形分布和故障情况

比较上面四种情况下的绕击跳闸率，发现同样的地面倾角情况下绕击跳闸率从大到小分别为跨谷、山顶、沿坡和爬坡。爬坡时绕击跳闸率随着地面倾角的增大呈现下降趋势，主要是由于当山体的角度增大时，山体对输电线路的屏蔽作用增大。跨谷比山顶的输电线路更容易遭受绕击，主要是由于输电线路在跨越山谷时对地的平均高度比较大。

长郑线全线总长56.242公里，大部分处于山地，共有铁塔140基，整理长郑线全线的地形和故障情况如表1所示，处于跨谷地形的有11基，处于山顶地形的有32基。近三年长郑线的绕击跳闸故障发生过一次，故障杆塔为长郑线104#，其地形为跨谷地形。可见，输电线路处于跨谷地形最危险，最易发生绕击。

4 结 论

(1)在相同的线路参数和地面倾角情况下，输电线路的绕击跳闸率从大到小分别是跨谷、山顶、沿坡、爬坡。对于爬坡的输电线路，绕击跳闸率随地面倾角的变大而减小，其余复杂地形的输电线路绕击跳闸率随地面倾角的变大而变大；

(2)通化地区输电线路的运行经验表明：跨谷地形是4种地形中最易发生绕击的地形。

[1] 曾嵘，何金良，陈水明.输电线路雷电防护技术研究(二)：分析方法[J].高电压技术，2009，35(12)：2910-2916.

[2] 吴广宁，熊万亮，曹晓斌，等.输电线路绕击特性的三维分析方法[J].高电压技术，2013，39(2)：374-382.

[3] 李瑞芳，吴广宁，曹晓斌，等.复杂地形输电线路绕击耐雷性能计算方法的改进[J].高压电器，2011，47(4)：96-100.

[4] 姚尧，李健，李涵，等.基于山区雷电先导发展的改进电气几何模型仿真研究[J].高电压技术，2015，41(5)：1550-1557.

[5] 中华人民共和国电力工业部.GB/T50064-2014交流电气装置的过电压保护和绝缘配合设计规范[S].北京：中国计划出版社，2014.

[6] 张志劲，司马文霞，蒋兴良，等.高杆塔下击距系数的研究[J].高电压技术，2005，31(4)：16-18.

[7] 李瑞芳，吴广宁，曹晓斌，等.山区输电线路雷电绕击跳闸率的计算[J].电网技术，2010，34(12)：142-146.

[8] 陈稼苗，钟一俊，劳建民，等.大跨越特高杆塔线路防雷设计中EGM的应用[J].高电压技术，2008，34(7)：1374-1378.

[9] 周远翔，鲁斌，燕福龙，等.山区复杂地形输电线路绕击跳闸率的研究[J].高电压技术，2007，33(6)：45-49.

[10] 耿屹楠，曾嵘，李雨，等.输电线路防雷性能评估中的复杂地形地区模型[J].高电压技术，2010，36(6)：1501-1505.

[11] 吕金煌，许宇航，陈钢.输电线路大档距、大转角、大高差杆塔防雷措施的探讨[J].水电能源科学，2010，28(10)：134-135.

[12] 李慧奇，田东阁，王平，等.微地形和输电线路绕击故障关系的研究[J].电瓷避雷器，2014(3)：73-83.

[13] 鲁志伟，马文婧，宋文国，等.新立变电站接地系统安全性能研究[J].东北电力大学学报，2012，32(6)：28-32.

[14] 赵淳，陈家宏，谷山强，等.山区复杂地形条件下输电线路雷击跳闸故障分析方法[J].电网技术，2011，35(12)：136-141.

CalculationofShieldingFailureFlash-overRateon220kVTransmissionLineinaMountainousArea

JiaRu1，WangChao2,LuZhiwei1，GaoJiayi3，LiBo1，LiXu1

(1.Electrical Engineering College,Northeast Electric Power University Jilin Jilin 132012；2.State Grid Tonghua Power Supply Company，Tonghua Jilin 134000；3.Lishen Power Battery Systems Company,Tianjin 300384)

Because of larger surface relief in mountainous area，lightning appears frequently，lightning shielding failure rate increases sharply.The calculation of lightning shielding failure flash-over rate is getting more difficult result from complex terrain of mountainous area.There are some innovations.Terrain of mountainous area will be divided into four categories：mountain ridge，hillside，installed from the mountain foot to mountain top and span valley.Lightning shielding failure flash-over rate is calculated and deduced by electro-geometric model under the circumstances.Especially，lightning shielding failure flash-over rate on transmission line which spans valley is quantified by logically approximated span valley terrain，and is proved that lightning shielding failure risk is higher than other terrain.220kV transmission line in Tonghua city has been taken as an example.The calculations and analyses of fault cases have verified that the calculation is correct and credible and compared affects of ground elevation and terrain on lightning shielding failure flash-over rate.

Mountainous area；Complex terrain；Shielding failure flash-over rate；Ground elevation

2017-02-12

2016年吉林省电力有限公司科技项目(SGTYHT/14-JS-188)

贾 茹(1992-)，女，在读硕士研究生，主要研究方向：高电压与绝缘技术.

电子邮箱：980016810@qq.com(贾茹)；13894531586@163.com(王超)；1443958749@qq.com(鲁志伟)；703794520@qq.com(高嘉义)；811756690@qq.com(李博)；2479289655@qq.com(李旭)

1005-2992(2017)06-0001-07

TM614

A