基于经验模态分解削弱多波束残余误差的方法

赵祥鸿，暴景阳，黄辰虎，黄贤源，陆秀平

（1.海军大连舰艇学院海洋测绘系，辽宁大连116018；2.海军海洋测绘研究所，天津300061）

基于经验模态分解削弱多波束残余误差的方法

赵祥鸿1，暴景阳1，黄辰虎2，黄贤源2，陆秀平2

（1.海军大连舰艇学院海洋测绘系，辽宁大连116018；2.海军海洋测绘研究所，天津300061）

针对多波束水深数据中存在的系统性残余误差，提出了基于经验模态分解方法来削弱残余误差的方法：首先利用经验模态分解方法对多波束测深数据作一维分解，将非线性、非平稳的多波束测深数据分解成准线性子波，然后构建水深数据趋势项与残余项，利用中央波束趋势项建立整体数据趋势项，最后加以水深数据残余项还原海底地形，削弱残余误差影响。通过实测多波束测深数据验证方法的有效性。

经验模态分解（EMD）；多波束；残余误差；趋势项；残余项

多波束测深系统是一个全覆盖式声纳测深系统，除自身测量误差之外，还受声速变化、定位和测船姿态、换能器安装偏差等误差影响（赵建虎等，2008）。目前国内外针对各种误差影响的改正措施已经有很多，赵建虎等（2001）分析了船姿对多波束测量的影响；阳凡林等（2010）分析了多波束测深瞬时姿态对水深的影响并提出相应的改正措施；孙文川等（2016）提出一种基于最小二乘的多波束换能器横摇偏差二次校正方法；张志伟（2016）等综合分析了多波束换能器安装偏差对海底地形测量的影响。

尽管在进行多波束数据处理的过程中，针对各项误差都有相应的改正措施，但是处理后的结果中仍然包含着残余系统性偏差，表现为相邻条带之间重叠区域内测深数据出现不匹配的情况。针对此问题，国内外专家学者提出了许多方法：吴自银等（2005）运用GIS面向对象方法分析了造成多波束边缘波束测量误差的原因；丁继胜等（2004）提出了一种误差强压制方法来解决相邻条带水深不符情况。但是，这些方法致力于解决相邻条带测深一致性的问题，没能从根本上削弱残余误差的影响。赵建虎等（2013）提出了一种基于地形变化长波项和短波项相结合的削弱残余误差方法，对于残余误差的削弱有很好的效果，但是其残余误差削弱原理较为复杂，实际操作计算量较大。

目前小波分析方法广泛应用于处理非平稳信号中，但是其在实际应用中存在许多问题，例如小波基函数的选择、分解层数的设置等，都需要根据以往的经验或者多次实验来确定，自适应性较差。经验模态分解方法是Huang等（1998）于1998年提出的一种数据处理方法，该方法能够基于数据本身的特点，将信号中不同尺度的波动或趋势逐级分解开来，产生一系列本征模态函数。其特点是可以处理非线性、非平稳过程的数据，适合处理多波束测深数据，并且该方法自适应性较好，任何复杂的信号都能被分解为有限数量的简单分量之和。因此，本文将经验模态分解方法引入到削弱多波束残余误差的工作中，利用经验模分解方法对多波束测深数据进行一维分解，建立经验模态函数与水深数据关系，削弱残余误差影响。

1 基于经验模态分解削弱残余误差的方法

1.1 经验模态分解方法

经验模态分解方法从本质上讲是对一个信号进行平稳化处理，其结果是将信号中不同尺度的波动或趋势逐级分解开来，产生一系列具有不同特征尺度的数据序列，每一个序列称为一个本征模态函数（IMF）（Echeverria et al，2001；Agarwal et al，2007；Battista et al，2007）。最低频率的IMF分量通常情况下代表原始信号的趋势。其大体思路是用波动上、下包络的平均值去确定“瞬时平衡位置”，进而提取出本征模态函数。对数据提取若干本征模态函数直至满足终止条件，其处理过程如图1：

本征模态函数需满足的两个条件：（1）在整个数据集中，极值数和过零数相等或最多差一个；（2）在任意点，由局部极大值构成的包络和由局部极小值构成的包络均值为零。为了使本征模态函数足够反映实际的振幅和频率，设定筛选停止条件：

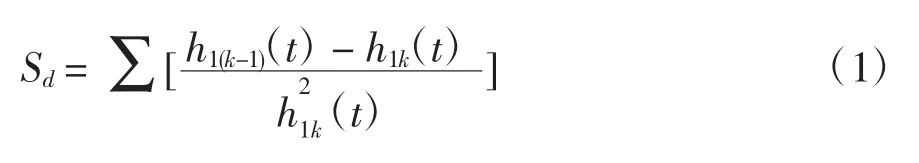
循环终止条件：通常有两个判断标准，一是所得到的本征模态函数或者残余分量小于预设的阈值时；或者当残余分量是单调函数时，不能再筛分出本征模态函数。

图1 经验模态分解流程

对于原始信号进行EMD运算，首先就要得到其上下包络，即根据信号极大极小值，用三次样条曲线进行逼近。在进行三次样条插值的时候，必然使得信号的上下包络在信号的两端附近严重扭曲，即端点飞翼问题。当处理低频或者多分量复杂信号时，会严重淹没信号的端部特征。为了抑制样条插值的端点飞翼，又不扭曲原始信号的端部特征，采用端点延拓的方法加以抑制（舒忠平等，2006；孙晖等，2005）。

1.2 残余误差削弱方法

多波束水深数据X（t）可以表示成由趋势项Q和残余项R组成，其中趋势项包括水深数据的主成分，即海底地形的总体趋势。

对多波束水深数据进行经验模态分解，将水深数据分解为若干经验模态函数（IMFi）和残余量R′。构建经验模态函数与水深数据趋势项关系如下：

进一步建立经验模态函数与水深数据的关系：

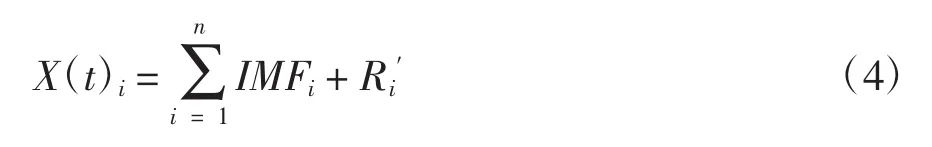
表达式中，n为经验模态分解的次数。多波束测深数据的残余误差主要表现为：两条相邻条带的重叠部分出现水深不符值。多波束测深系统进行水深数据采集，通常中央波束采集的数据质量较好。利用两相邻条带中央波束的趋势项来拟合边缘波束（重叠部分），加以残余项还原海底地形，具体步骤如下：

（1）提取多波束水深数据中相邻两条带数据，以其中一个条带的正中波束为基点，采用最小距离法寻找相邻条带直线距离最近的点，找出对应的另一条带ping断面的ping断面。由于航速和航向等问题，导致相邻条带的ping断面并不严格对应，针对这种情况本文选取相邻的ping断面与之相对应。

（2）对两条带之间同一ping断面上的数据X（t）1、X（t）2分别进行经验模态分解，通过上述方法得到两条带水深数据趋势项Q1、Q2和残余项R1、R2。分别截取趋势项Q1、Q2中的中央波束部分M1、M2和边缘波束部分L1、L2（中央波束的波束入射角选择为0°≤φ≤35°，通常认为在这个波束入射角范围内，水深数据质量最好，可靠性最高），如图2所示：

图2 两条带水深数据趋势项

（3）对中央波束趋势项M1、M2拟合出对应的边缘波束的趋势项L，逐个循环各个ping对，从而获得两条带的总体趋势项，具体拟合方程如下：

（4）构建总体趋势项Q=Q1+Q2+L，加上残余项还原海底地形。

2 实验验证与分析

2.1 实验准备

实验数据来源于某海域实测数据，多波束测深系统每ping包含193个波束，纵横波束角均为1.5°，波束开角为140°，采用等角度发射接收的模式。实验选取两条测线各包含500 ping水深数据，如图3所示，可以看出两条带重叠部分出现明显不符情况（为了更好的表现残余误差的削弱效果，前期已经进行了测深异常值的剔除工作）。

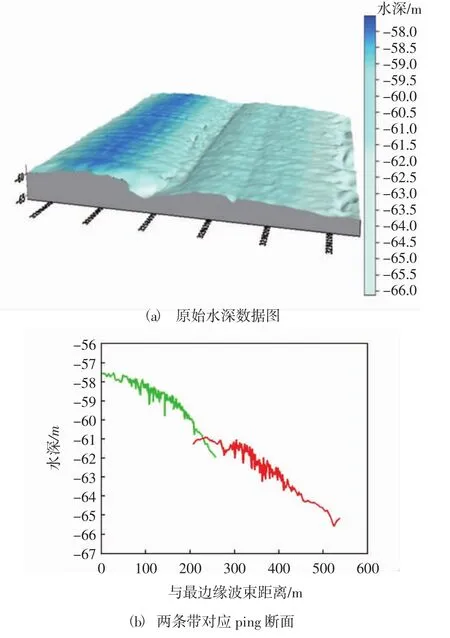
图3 两条测线原始水深数据及对应ping断面

2.2 实验过程及分析

依据前文所述方法，分别对两条带数据进行经验模态正交分解，提取本征模态函数，构建水深数据趋势项和残余项，具体步骤如下：

（1）先识别出每ping水深数据X（t）中的所有极大值点和极小值点，分别利用插值拟合出信号的上包络线Xmax（t）和下包络线Xmin（t），计算上下包络线的平均值m（t），如图4所示：

图4 单ping水深数据及拟合的上下包络线与平均值

图5 单ping水深数据及所得4个模态函数IMFi和残余量R′

（2）用原始水深数据X（t）减去平均值m（t）得到类距平均值h（t），如果h（t）满足IMF所规定的条件，那么h（t）即为分解出的第一个模式分量，否则，将h（t）作为原始数据继续重复上述计算，直到满足IMF的条件。

（3）得到第一个经验模态函数，将原始水深数据剥离经验模态函数作为新的数据，重复步骤（1）和（2），直到满足循环结束条件，得到4个模态函数IMFi以及残余量R′，如图5所示：

图5中，横坐标表示为ping断面上各个水深点与最边缘波束点的距离，纵坐标表示水深值。图5（a）是多波束单ping水深数据，图5（b）-图2.3（e）是经过经验模态分解得到的本征模态函数，得到的残余量R′如图5（f）所示。经验模态分解将信号中不同尺度的波动逐级分解开来，分解产生的本征模态函数代表水深数据的不同频率特征，由高频至低频依次为IMF1、IMF2、IMF3、IMF4，残余分量R′中的频率最低。

分别对选取的两条测线进行经验模态分解，将得到的两组本征模态函数（IMFi1、IMFi2）及残余量R1′、R2′，依据式（4）构建两条带水深数据趋势项Q和残余项R如图6所示。

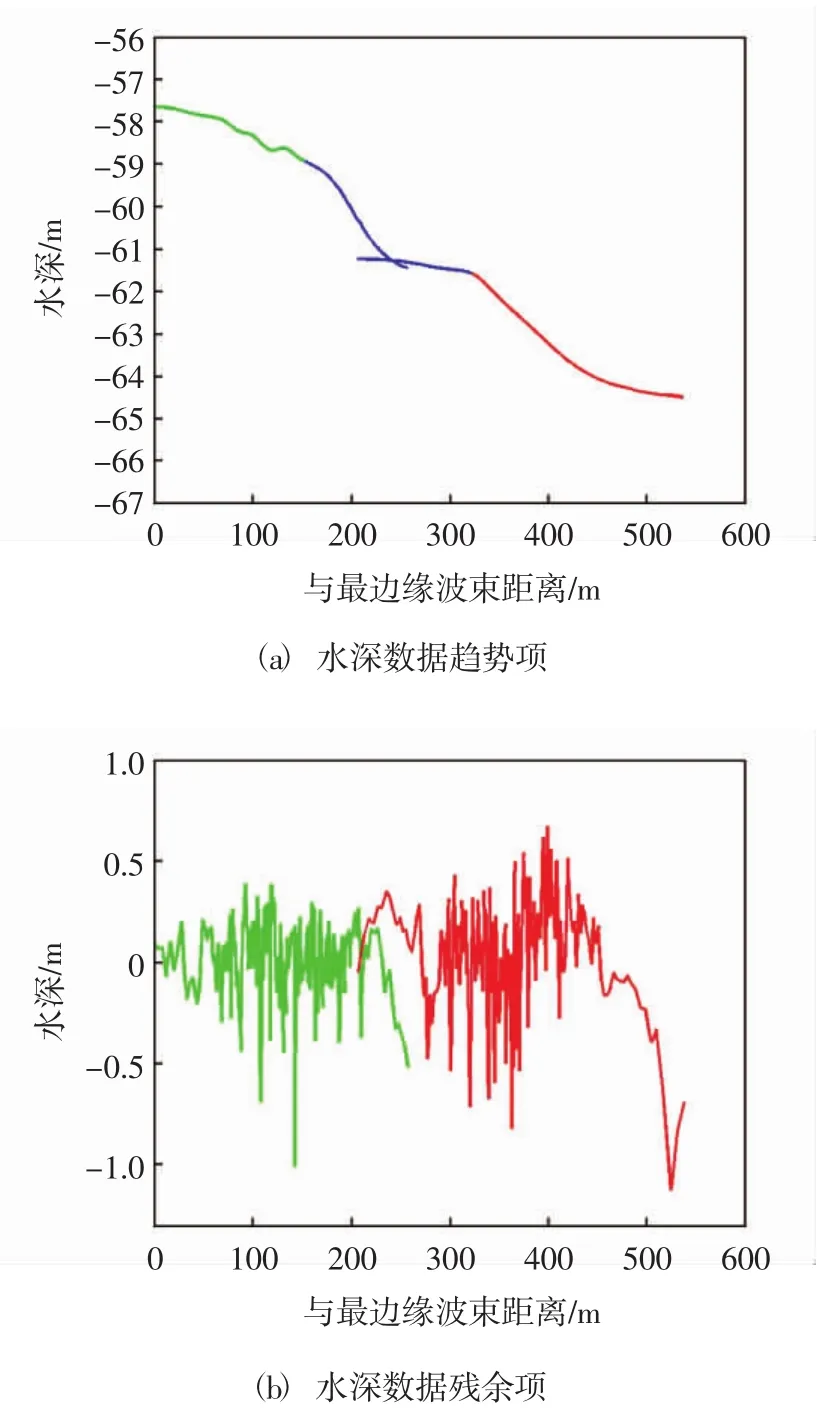
图6 两条带水深数据趋势项及残余项

图6（a）中蓝色曲线代表两条带水深数据边缘波束部分，利用两条带中央波束趋势项拟合边缘波束趋势项求得表达式的系数，拟合图如图7，具体方程表达式如下：

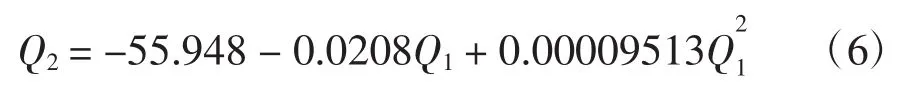
将重构的总体水深数据趋势项加以总体残余项还原水深数据，还原后的单ping水深数据效果如图8，与图3（b）比较发现，两条带水深数据中存在的残余误差得到削弱。

图7 水深数据趋势项

图8 融合后的单ping对水深数据

（4）采用最小距离法寻找条带之间对应的ping断面。截取相邻两条带测线数据，分别提取两条航迹线正中波束对应的位置信息；以其中一条测线的波束位置为基点，在相邻测线中寻找直线距离最近的点，其对所在的波束即为对应的波束。在两条带逐个循环各个ping对重复上述工作，那么整个水深数据的残余误差得以削弱。削弱残余误差影响后的海底地形，效果如图9。

比较图9与图3，水深数据中残余误差得到较好的削弱，证明了基于经验模态分解削弱残余误差方法的可行性。量化反映残余误差削弱效果如表1所示。

表1中可以看出，经过残余误差改正后的相邻条带不符值的范围比改正前有所缩小；不符值均值的绝对值和均方误差值为改正前的一半左右；表明经过经验模态分解方法可以有效构建多波束水深数据趋势项及残余项，削弱残余误差的影响。

图9 削弱残余误差影响后的海底地形

表1 相邻条带不符值统计

3 结论

多波束残余误差表现为相邻条带重叠水深数据的不符，本文利用经验模分解的方法对多波束测深数据进行一维分解，将非线性的多波束测深数据分解成准线性的子波。通过提取测深数据趋势项构建经验模态函数与水深数据关系，并通过实验验证该方法可有效削弱残余误差的影响。

Agarwal,V,Tsoukalas,L.H,2007.Denoising electrical signal via empirical mode decomposition.2007 Irep Symposium－Bulk Power SystemDynamicsandControl－ViiRevitalizingOperational Reliability,1－2:72－77.

Battista.B.M,Knapp,C,McGee,T,et al,2007.Application of the empirical mode decomposition and Hilbert－Huang transform to seismic reflection data.Geophysics,72(2):H29－H37.

Echeverria,J.C.,Crowe,J.A.,Woolfson,M.S,et al,2001.Application of empirical mode decomposition to heart rate variability analysis.Medical&Biological Engineering&Computing,39(4):471－479.

Huang N E,Shen Z,Long S R,et al,1998.The empirical mode decompositionandtheHilbertspectrumfornonlinearand nonstationary time series analysis.Pro.Roy.Soc.Lond,Ser.A454:903－995.

丁继胜,2004.基于等效声速剖面法的多波束测深系统声线折射改正技术.海洋测绘,24(6):27－30.

黄辰虎,2016.联合XBT和WOA13模型盐度信息的深水走航声速准确确定.海洋通报,2016(35):554－561.

舒忠平,杨智春,2006.抑制经验模态分解边缘效应的极值点对称延拓法.西北工业大学学报,24(5):639－642.

孙晖,2005.经验模态分解理论与应用研究.杭州,浙江大学.

孙文川,暴景阳,金绍华,等,2016.多波束换能器横摇偏差二次校准的一种方法.武汉大学学报,41(11):1－5.

吴自银,金祥龙,郑玉龙,等,2005.多波束测深边缘波束误差的综合校正.海洋学报,27(4):88－94.

阳凡林,卢秀山,李家彪,等,2010.多波束勘测运动传感器偏移的改正方法.武汉大学学报,35(7):816－820.

张志伟,暴景阳,肖付民,2016.多波束换能器安装偏差对海底地形测量的影响.海洋测绘,36(1):51－54.

赵建虎,刘经南,2008.多波束测深及图像数据处理.武汉:武汉大学出版社:101－110.

赵建虎,刘经南,张红梅,2001.船姿分析及其对多波束测量的影响.武汉大学学报,26(2):144－149.

赵建虎,张红梅,严峻,等,2013.削弱残余误差对多波束测深综合影响的方法研究.武汉大学学报,38(10):1184－1187.

Weakening effect of residual error based on EMD

ZHAO Xiang-hong1,BAO Jing-yang1,HUANG Chen-hu2,HUANG Xian-yuan2,LU Xiu-ping2
（1.Department of Hydrography and Cartography,Dalian Naval Academy,Dalian 116018,China;2.Naval Institute of Hydrographic Surveying and Charting,Tianjin 300061,China）

This paper puts forward a method for weakening the effect of residual errors of multibeam bathymetric data based on Empirical Mode Decomposition（EMD）.Multibeam bathymetric data is deposed into one-dimensional linear waves by EMD.In that way,the trend and residual of seabed topography is constructed.The trend of whole data is constructed using the center beam trend.Then submarine topography is restored by merging of the data trend and the residual one,which weakens the influence of residual errors.The paper also shows an experiment to prove effectiveness of the method.

Empirical Mode Decomposition（EMD）;multi-beam bathymetric data;residual errors;trend of seabed topography;residual of seabed topography

P733.2；P229

A

1001－6932（2017）06－0662－06

10.11840/j.issn.1001-6392.2017.06.008

2016-09-28；

2017-05-26

国家自然科学基金（41474012）；国家重大科学仪器设备开发专项（2011YQ12004503）。

赵祥鸿（1989-），博士研究生，主要从事海底地形测量数据处理研究。电子邮箱：zhaoxianghong0@163.com。

袁泽轶）