波浪对并联双箱作用的耦合水动力共振分析
姜胜超, 宗 智, 邹 丽
(1.大连理工大学船舶工程学院,辽宁 大连 116024; 2.高新船舶与深海开发装备协同创新中心,上海 200240)
波浪对并联双箱作用的耦合水动力共振分析
姜胜超1,2, 宗 智1,2, 邹 丽1,2
(1.大连理工大学船舶工程学院,辽宁 大连 116024; 2.高新船舶与深海开发装备协同创新中心,上海 200240)
基于OpenFOAM研究了波浪作用于并联双箱时的水动力共振问题。主要研究了共振条件下自由水面非线性以及流体黏性对双箱间波高的影响。数值模拟显示,线性势流理论对共振波高的过高估计不仅由于其忽略了流体的黏性,也由于忽略了自由水面非线性的影响。当以共振频率入射时,随着入射波高的增大,更多的能量被反射,导致双箱间相对共振波高以及相对能量耗散的减小。当入射波浪偏移共振频率但仍在共振频率附近时,相对能量耗散成为双箱间相对波高降低的主要因素。总之,在共振条件下,自由水面非线性和流体黏性均有重要的影响。
流体共振;非线性作用;能量耗散
0 引 言
船舶水动力问题是海洋工程领域的重要研究课题。近些年,随着海上石油与天然气的开采逐渐向深海及恶劣海洋环境发展,超大型生产船舶,如浮式生产储油卸油装置(FPSO)以及浮式液化天然气生产系统(FLNG)等被大量使用。这些大型船舶通常采用伸展锚或牵索塔系泊作业,并通过联合作业的形式将开采的石油或液化天然气装卸到穿梭油轮或液化天然气船(LNG)上,再将其运送到陆地。在船舶联合作业的过程中,在特定的入射波浪频率下,船舶间的流体会发生大幅震荡运动,同时船舶所受到的波浪力也会显著增大,甚至产生水动力共振现象,这对联合作业的生产效率会产生影响,也会对船舶联合作业的安全造成潜在的威胁。另外,大型船舶本身,如FPSO的月池、双体船与多体船,以及超大型浮体各安装模块之间也均有类似的共振现象发生。因此,开展船舶联合作业的水动力干涉共振问题的研究具有非常广泛的工程实践应用背景;同时,这一方面研究工作的开展对促进波浪与结构物相互作用理论的发展也具有非常重要的科学意义。
对于上述问题,线性势流模型可以预测一个较为准确的共振频率,但经常过高估计共振波高。一般认为势流理论使用的无黏无旋假设是其过高估计方箱间流体共振波高的主要原因。基于该分析,首先开展在传统势流理论所预测的不真实的共振波面位置处直接加入人工阻尼的近似计算方法[1—3],该方法可以降低传统势流理论所计算的不真实的共振波高,但是仍然不能反映流体共振的物理本质。因此,诸多学者使用计算流体力学与物理模型试验方法对该问题进行了研究[4—8],研究发现,能量耗散最主要发生在窄缝的底部,而不是在窄缝的自由水面。通过在窄缝底部的方箱结构中增加凸起可以加剧流体的涡旋运动,增加流体的能量耗散,从而有效地降低窄缝内流体的共振波高。
上述工作主要是基于流体黏性及有旋运动对共振问题的影响。其实,真实流体运动过程中的自由水面非线性也是一个非常重要的问题,这也是传统线性势流理论所忽略的问题。因此,陆续开展了使用非线性势流方法对窄缝共振问题的研究工作[9—10]。数值结果显示,尽管自由水面非线性在压制线性势流理论的过高估计的共振波高方面很有限,但窄缝共振与非线性刚性弹簧体系具有类似的现象,即随着入射波陡的增加,共振频率向高频移动,这也是典型的非线性作用的结果。上述结果均表明,在发生共振时,自由水面非线性也会对流体共振产生重要影响。但是,当发生共振时,自由水面非线性与流体有旋运动将同时产生作用,简单地只考虑其中一个因素对共振现象的影响是不全面的。

1 控制方程与数值方法
采用计算流体力学方法研究波浪对并联双箱作用的耦合水动力的共振问题,考虑不可压缩的黏性两相流问题,由于涉及网格运动,因此在任意拉格朗日-欧拉(ALE)理论的观点下对Navier-Stokes方程重新推导,其形式为
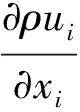
(1)

(2)
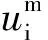
为使模型能够满足波浪破碎时的模拟要求,采用VOF方法对自由水面运动进行捕捉。定义流体相函数φ:

(3)
它满足ALE理论下的边界面方程
(4)
进而可确定两相流的密度及动力黏性系数分布为
(5)
式中: 下标w和a分别代表水和空气,即ρw和ρa分别为水与空气的密度;μw和μa分别为水与空气的动力黏性系数。在数据处理时,取φ=0.5等值线作为液体的自由水面。
对两相流控制方程式(1)、式(2)及界面方程式(4)采用有限体积法(FVM)离散,其中时间离散采用欧拉格式,散度和梯度计算分别使用Gauss Vanleer和Gauss linear格式。扩散项使用Gauss linear corrected格式。Navier-Stokes方程的求解采用PISO (Pressure implicit with splitting of operators)方法[11],其中,速度方程可直接采用代数方法求解,压力方程则采用BI-CGSTAB[12]方法迭代求解。
2 数值模型设置与验证
图1为波浪与并联双箱作用的数值模型示意图,其中,坐标系定义在双箱间流体静水面位置处,x轴从左指向右,为波浪传播方向;y轴指向上方。并联双箱断面定义为A箱和B箱,宽度B为0.50m,吃水深度分别为DL和DR,放置于水深h为0.50m的水槽中。双箱间距Bg为0.050m,当波浪以某种特定频率入射时,双箱间流体将发生较大的共振运动,这是本文主要的研究内容。
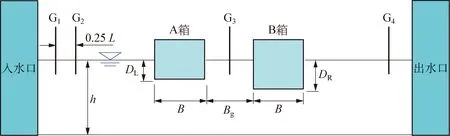
图1 数值模型示意图Fig.1 Sketch of the definition of the numerical wave flume
在本文中,选取DL=0.103 m和DR=0.202 m组合,以及DL=0.202m和DR=0.103m两种组合工况,结合三种入射波幅Ai=0.008m, 0.012m和0.016m进行研究。入射波浪频率基于Saitoh等[13]的实验结果以及Lu等[4]的有限元数值结果进行选取。在数值计算中,布置4台浪高仪G1~G4对自由水面进行量测,G1和G2用于分离入射波和反射波,两者间隔保持为0.25L,其中L为入射波波长;G3用于测量双箱间的自由水面波高Ag,放置于坐标系原点位置处;G4则用于测量透射波;G2和G4点分别放置于远离A箱和B箱外侧1.5L位置处。
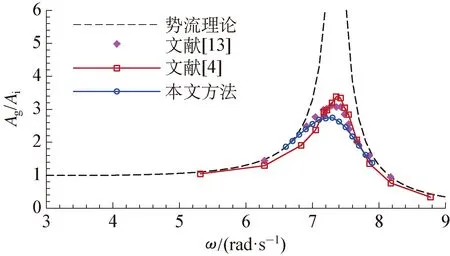
使用上述模型对入射波幅Ai=0.012m,双箱吃水DL=DR=0.103和0.252m的情况进行验证,为验证使用黏性流模型的必要性,图2中加入了线性势流理论的结果。首先对G3处的波面随入射波浪频率的变化进行对比,可以看出,势流理论可以准确预测共振频率,但显著高估了共振波高,但本文黏性流模型与Saitoh等[13]的实验结果以及Lu等[4]的有限元数值结果均符合良好,证明了本文方法的正确性。
(a) DL=DR=0.103m
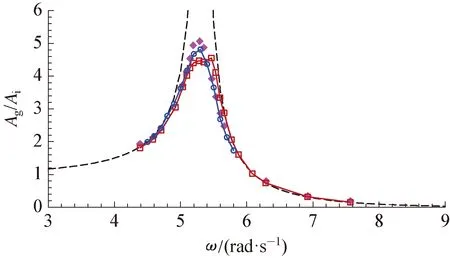
(b) DL=DR=0.252m图2 浪高仪G3处自由水面波高随频率变化的数值验证Fig.2 Numerical validation for free surface amplitude
进一步考虑入射系数Kr和透射系数Kt的计算结果,选取DL=DR=0.252m的情况进行对比,如图3所示,图中同样对比了线性势流理论的结果。从图3(a)中可以看出,势流模型与黏性流模型的反射系数计算结果均在共振频率附近有一极小值,该极小值所在频率对应双箱间流体的共振频率。黏性流模型所给出的反射系数随频率的变化与实验结果符合很好,但是,势流模型在共振频率附近低估了反射系数值。透射系数的结果如图3(b)所示,势流模型在共振频率处预测了一极大值,这主要是双箱间共振流体辐射作用的结果。但是,从实验及黏性流结果可以看出,由于双箱间共振波高并未出现极大值,不会在结构后方出现较强的辐射作用,因此,势流理论所预测透射系数的极大值并未真实出现。该结果是实际波浪与并联双箱作用的结果,说明黏性流模型可以准确对其进行模拟,而线性势流理论则无法对其进行准确的模拟。
图2和图3的对比验证了本文采用的势流模型可以准确预测双箱间流体的共振波高、透射系数与反射系数,而黏性流模型过高地估计了共振波高值以及透射系数和反射系数的极值。上述验证结果表示,数值模型可以对该问题进行准确模拟,且所得结果可以应用于后文的数值对比。
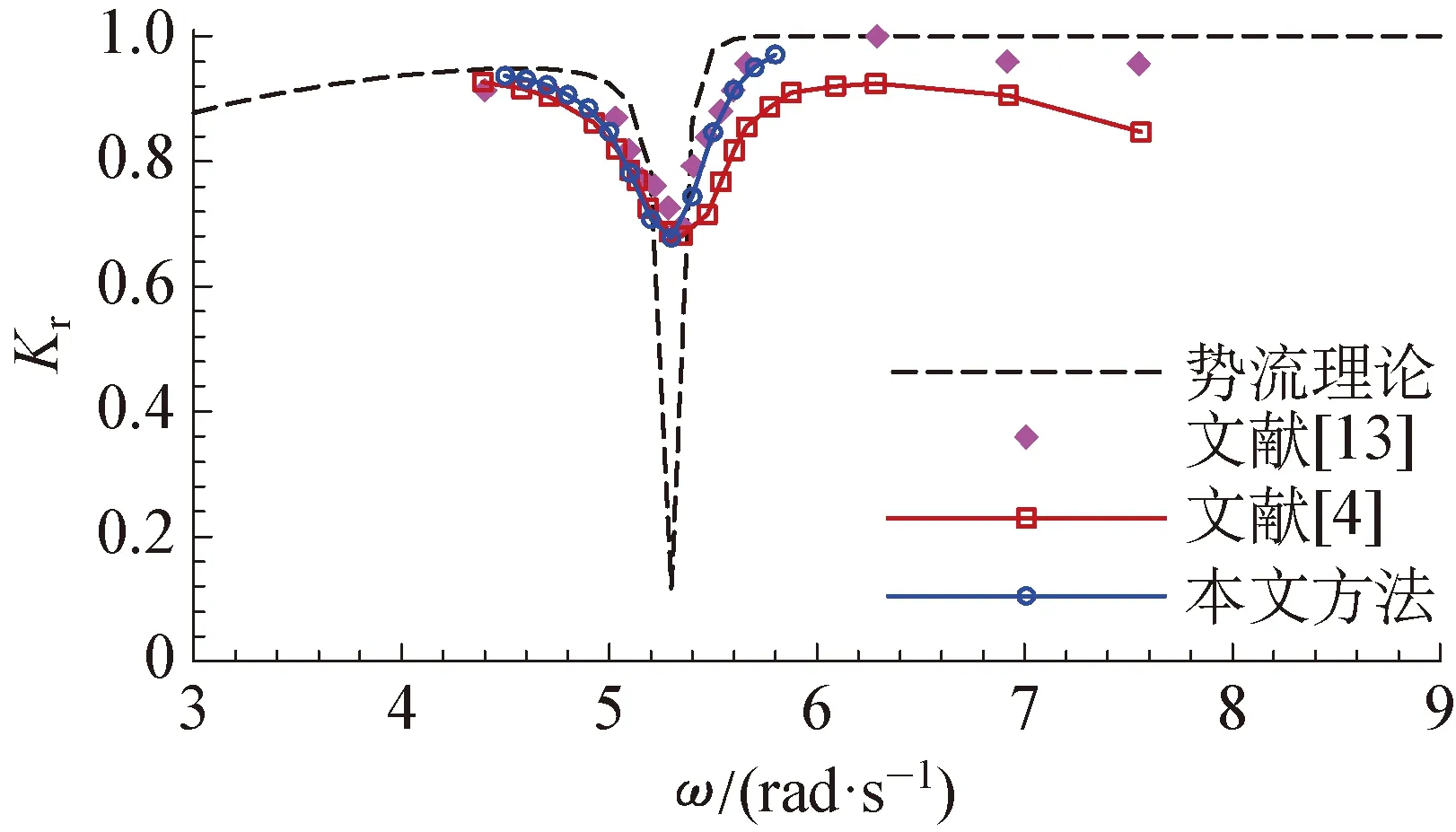
(a) 反射系数

(b) 透射系数
3 数值分析
3.1 入射波浪频率对双箱间流体共振响应的影响
将上述数值模型应用于波浪对不同尺寸双箱作用的计算中。如前所述,选取DL=0.103m和DR=0.202m,以及DL=0.202m和DR=0.103m两种组合工况进行研究。图4所示为入射波幅Ai=0.012m时G3浪高仪处无因次波面随频率的变化,可以看出,与黏性流结果相比,势流理论可以准确预测共振频率,但其明显高估了共振频率附近的波面高度。其主要原因是其使用线性模型,忽略了流体有旋运动所产生的能量耗散以及自由水面运动所产生的非线性效应。而黏性流模型可以准确地对其进行预测,因此可获得较准确的共振波高计算结果。

(a) DL=1.03m, DR=0.202m
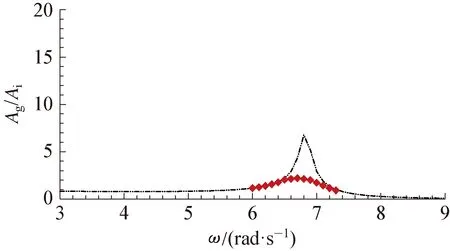
(b) DL=0.202m, DR=0.103m
进一步考虑反射系数Kr及透射系数Kt随入射波浪频率的变化。如图5所示,势流理论在共振频率处分别为反射波与入射波预测了极小值和极大值,这实际上高估了真实的结果。对于透射系数,在黏性流结果中几乎很难识别势流理论在共振频率附近所预测的极大值,这是由于透射波主要来自于双箱间自由水面的大振幅运动,该大振幅运动作为透射波的辐射源,生成了后方的辐射波。势流理论由于过高估计了该辐射源,因此过高估计了辐射波。而在实际情况下,由于流体黏性的耗散作用以及波浪自由水面非线性的反射作用,双箱间流体共振振幅相对较小,因此对后方辐射作用较弱,不会发生势流理论所预测的显著峰值。该过程是真实的流体运动能量的耗散以及转移过程,黏性流理论可以准确地对其进行模拟。

(a) DL=1.03m, DR=0.202m

(b) DL=0.202m, DR=0.103m图5 入射波幅Ai=0.012m时反射系数Kr及透射系数Kt随入射波浪频率的变化Fig.5 Comparison of reflection and transmission coefficients
从图5中可以看出,对于反射系数,势流结果和黏性流结果的差别与双箱吃水情况直接相关,对于上游箱体吃水小于下游箱体吃水的情况[见图5(a)],黏性流结果的反射系数在共振频率附件总是小于势流结果,这是由于双箱间的缝隙直接暴露于波浪作用中,因此产生较大的波浪运动,会导致较大的能量耗散。由于入射波所含的能量用于支持能量耗散作用,因而导致反射系数减小。对于上游箱体吃水大于下游箱体吃水的情况[见图5(b)],黏性流结果的反射系数在共振频率附近总是大于势流结果,这是由于上游箱体吃水较大,对双箱间的缝隙具有保护作用,具体表现为波浪作用于上游箱体后直接发生反射,反射系数增大,使缝隙内波高相对较小。

(a) DL=1.03m, DR=0.202m

(b) DL=0.202m, DR=0.103m图6 入射波幅Ai=0.012m时能量系数随入射波浪频率的变化Fig.6 Comparison of energy coefficients
3.2 入射波浪振幅对双箱间流体共振响应的影响
为研究流体运动能量耗散以及波浪自由水面非线性对流体共振的影响,考虑不同入射波幅条件下双箱间流体运动振幅、透射系数和反射系数以及能量系数随入射波浪频率的分布。首先考虑入射波幅对双箱间流体运动振幅的影响,如图7所示。从图中可以看出,在共振频率附近,双箱间流体无因次运动振幅随入射波幅的增大而减小,当入射波浪频率远离共振频率时,不同入射波幅下的无因次波浪运动振幅基本相同。从本文计算结果还可以看出,入射波幅作用下,双箱间流体共振频率几乎没有发生改变。

(a) DL=1.03m, DR=0.202m

(b) DL=0.202m, DR=0.103m
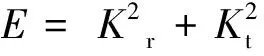

(a) DL=1.03m, DR=0.202m
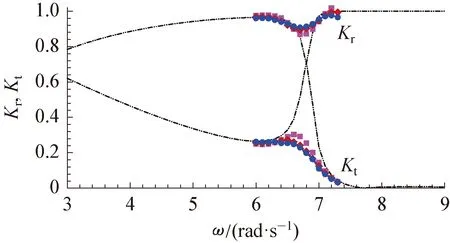
(b) DL=0.202m, DR=0.103m

(a) DL=1.03m, DR=0.202m

(b) DL=0.202m, DR=0.103m
进一步对比图7和图8中入射波频率接近但不等于共振频率时不同入射波高对反射系数、透射系数以及能量系数的影响,可以看出,入射波幅的增大,透射系数和反射系数均减小,即能量系数减小,意味着更多的能量耗散发生,此时能量耗散在流体运动过程中占有统治地位。因此,流体运动能量耗散以及波浪自由水面非线性均会对流体共振产生重要影响,在不同频率时,两者具有不同的决定性影响。
4 结 语
基于OpenFOAM对波浪作用下并联双箱的水动力共振问题进行了数值模拟,重点对共振发生时的能量转移及耗散过程进行了分析。数值结果表明,势流模型过高地估计了共振波高和透射系数,反射系数则根据不同双箱尺寸表现不同的特征。共振频率下波浪的自由水面非线性随着入射波幅的增大而增强,波浪作用于物体后有更多的能量被反射,传播到双箱间共振流体内的能量减小,双箱间流体共振波高降低,同时导致能量耗散减小,共振频率下由于自由水面非线性所导致的能量转移过程在该过程中占统治地位。当入射波频率接近但不等于共振频率时,透射系数、反射系数以及能量系数均减小,更多的能量耗散发生。此时能量耗散在流体运动过程中占有统治地位。总之,流体运动能量耗散以及波浪自由水面非线性均会对流体共振产生重要影响。
[1] Newman J N. Progress in wave load computations on offshore structures [R]. 23th OMAE Conference, Vancouver, 2014.
[2] Chen X-B. Hydrodynamics in offshore and naval applications-part I [R]. International Conference on Hydrodynamics, Perth, 2004.
[3] Fournier J R, Naciri M, Chen X-B. Hydrodynamics of two side-by-side vessels experiments and num simulations [C]. ISOPE, 2006: 349.
[4] Lu L, Cheng L, Teng B, et al. Numerical investigation of fluid resonance in two narrow gaps of three identical rectangular structures [J] Applied Ocean Research, 2010,32(2): 177.
[5] Lu L, Chen X. Dissipation in the gap resonance between two bodies [C]. 27th International Workshop on Water Waves and Floating Bodies, 2012: 22.
[6] Kristiansen T, Faltinsen O M. A two-dimensional numerical and experimental study of resonant coupled ship and piston-mode motion [J]. Applied Ocean Research, 2010,32(2): 158.
[7] Moradi N, Zhou T, Cheng L. Effect of inlet configuration on wave resonance in the narrow gap of two fixed bodies in close proximity [J]. Ocean Engineering, 2015,103: 88.
[8] Fredriksen A G, Kristiansen T, Faltinsen O M. Experimental and numerical investigation of wave resonance in moonpools at low forward speed [J]. Applied Ocean Research, 2014,47: 28.
[9] Faltinsen O M, Rognebakke O F, Timokha A N. Two-dimensional resonant piston-like sloshing in a moonpool [J]. Journal of Fluid Mechanics, 2007,575: 359.
[10] Feng X, Bai W. Wave resonances in a narrow gap between two barges using fully nonlinear numerical simulation [J]. Applied Ocean Research, 2015,50: 119.
[11] Issa R I. Solution of the implicitly discretised fluid flow equations by operator-splitting [J]. Journal of Computational Physics, 1991,93(2): 388.
[12] Van Der Vorst H A. BI-CGSTAB: a fast and smoothly converging variant of BI-CG for the solution of nonsymmetric linear system [J]. SIAM Journal on Scientific and Statistical Computing, 1992,12(2): 631.
[13] Saitoh T, Miao G, Ishida H. Theoretical analysis on appearance condition of fluid resonance in a narrow gap between two modules of very large oating structure [C]. Proceedings of the Third Asia-Pacific Workshop on Marine Hydrodynamics, 2006: 170.
WaveResonancebetweenTwoShipswithNon-IdenticalDraft
JIANG Sheng-chao1,2, ZONG Zhi1,2, ZOU Li1,2
(1.SchoolofNavalArchitecture,DalianUniversityofTechnology,Dalian,Liaoning116024,China; 2.CollaborativeInnovationCenterforAdvancedShipandDeep-SeaExploration,Shanghai200240,China)
Wave resonance in the narrow gap between two side-by-side non-identical ships is investigated by employing a two-dimensional numerical wave flume based on OpenFOAM package. The focus of this study is to examine the influence of free surface nonlinearity and fluid viscosity on the hydrodynamic behavior of wave response at around resonant conditions. Numerical simulations show that the unrealistic resonant amplitudes in the narrow gap by linear potential model are not only from the energy dissipation due to vortical motion, but also from the nonlinearity due to free surface. With the increase of incident wave steepness, more relative energy is reflected, leading to the decrease of relative resonant amplitude and relative energy dissipation in the narrow gap at resonant frequency. When the incident wave frequency is outside a little band to resonant frequency, relative energy dissipation becomes the dominant factor for the decrease of relative wave amplitude in the narrow gap with the increase of incident wave amplitudes. In a word, both the free surface nonlinearity and fluid viscosity play the important, but different, roles on wave resonances in the narrow gap.
fluid resonance; nonlinearity; energy dissipation
2017-04-28
中央高校基本科研业务费专项资金[DUT16RC(3)063]
姜胜超(1984—),男,博士,副教授,主要从事波浪对海上结构物作用方面的研究。
U661.1
A
2095-7297(2017)03-0150-07

