圆空心钢管混凝土短柱在轴向压力作用下的可靠性分析
王宏伟 陈少杰 周云

摘 要:为分析圆空心钢管混凝土短柱在轴向压力作用下的可靠性,以笔者及其他学者所进行的圆空心钢管混凝土轴压短柱试验数据为统计样本,结合Normal、Lognormal、Weibull、Gamma 4种分布形式,考虑模型误差,分别根据《钢管混凝土结构技术规范》(GB 50936—2014)中的钢管混凝土柱轴压承载力计算公式与作者提出的修正公式,运用Monte Carlo法计算得到了规范公式与修正公式的可靠度指标。结果表明:依据两种公式计算得到的可靠度指标均基本满足目标可靠度指标3.7的要求;规范公式的可靠度指标较大,约为修正公式的1.05倍,计算结果较为可靠;可靠度指标随着混凝土强度和荷载效应比的提高而上升,随着含钢率的提高而下降,钢材强度和空心率的变化,可靠度指标的变化不明显。考虑上述4种分布类型对抗力误差的影响,分析了各参数因素对抗力分项系数的影响,结果表明:计算模型误差分布类型和活载类型对抗力分项系数的影响不明显,安全等级和荷载效应比影响较为明显;考虑实际工程中常用的荷载效应比,提出荷载效应比不同时抗力分项系数取值分别为1.21、1.32、1.41。
关键词: 钢管混凝土短柱;轴向压力;模型误差;可靠性分析
中图分类号:TU311.2
文献标志码:A 文章编号:1674-4764(2018)06-0098-10
Reliability analysis of circular hollow concrete filled steel tube
short column under axial compression
Wang Hongwei1, Chen Shaojie1,Zhou Yun1
(School of Civil Engineering, Guangzhou University, Guangzhou 510006, P.R. China)
Abstract:In order to analyze the reliability of circular hollow concrete filled steel tube short column under axial compression, the experimental results as well as the data sets from literatures were collected. The model errors were taken into consideration via Normal, Lognormal, Weibull, Gamma distribution assumptions. Reliability analysis was carried out based on Technical Code of Concrete Filled Steel Tube Structure and the modified formula presented by the authors. Monte Carlo sampling was also performed and the calculated reliabilities satisfy the target reliability index. The reliability index of the code formula is greater than that of the modified formula within 5%. As the concrete strength and loading ratio increase, the reliability index increases. The reliability index decreases with the reduced steel ratio. The hollow ratio and steel strength have marginal influence on the reliability index. Parameter analysis was also carried out in considering the influence of model error distribution types, which indicated that mode error and live load type have less significant influence on partial factor of resistance, than the safety levels and the loading ratio. The partial factor of resistance under different loading ratios should be 1.21, 1.32 and 1.41, respectively.
Keywords: concrete filled steel tube short column; axial compression; model error; reliability analysis
鋼管混凝土构件具有承载力高,抗震性能、防火性能和抗冲击性能优越,截面尺寸小,自重轻等优点,在建筑结构中广泛应用。2001年实施的《建筑结构可靠度设计统一标准》(GB 50068—2001)规定:结构设计可采用以概率论为基础的极限状态设计原则,以保证结构的可靠度。2014年《钢管混凝土结构技术规范》(GB 50936—2014)[1] 开始实施。该规范提出了钢管混凝土构件在轴向压力作用下的承载力计算公式,为钢管混凝土结构的设计和施工提供了指导。
影响结构可靠度的因素主要有计算模型误差、材料性能误差、几何参数误差和荷载误差。钢筋混凝土结构在抗弯、抗剪、抗震时的可靠度已有研究[2-4] ,钢结构的可靠度分析和设计已较为成熟[5-6] 。对于钢管混凝土结构,Beck等[7] 根据各国规范的钢管混凝土构件的轴压承载力计算公式进行了可靠度分析,考虑了模型误差、钢材强度、混凝土强度、恒载和活载等随机参数的影响。Stewart等[8] 提出以Normal、Lognormal、Weibull和Gamma分布拟合模型误差,提高了结构可靠度分析的准确性。Zhai等[9] 采用该分布类型对配筋混凝土砌块墙进行了在压力和剪力作用下的可靠度分析。查晓雄等[10] 通过建立钢管混凝土构件的材料设计指标,对实心构件在轴压和轴拉作用下进行了可靠度分析。余敏等[11] 以试验数据为基础,利用一次二阶矩法对圆形和方形实心钢管混凝土构件进行了轴压承载力的可靠度分析。而关于空心钢管混凝土构件的可靠度分析还十分缺乏。
根据《钢管混凝土结构技术规范》(GB 50936—2014)提出的空心圆形钢管混凝土柱承载力计算公式和课题组提出的修正公式[12] ,利用Monte Carlo法对空心钢管混凝土轴压短柱进行可靠度分析。分析了计算模型误差类型、含钢率、混凝土强度、 钢管强度、荷载效应比、荷载类型等因素对可靠指标的影响。并分析了计算模型误差、活载类型、安全等级和荷载效应比等因素对抗力分项系数的影响。
1 钢管混凝土柱的承载力计算
1.1 规范计算公式
《钢管混凝土结构技术规范》(GB 50936—2014)[1] 中规定,圆形截面空心钢管混凝土轴压承载力按式(1)~式(2)计算。
N 0=(1.212+Bθ+Cθ2)f c A sc (1)
α sc =A s /A c (2)
θ=A s /A c ×f y/f c (3)
B=0.106f y/213+0.584 (4)
C=-0.037f c /14.4+0.011 (5)
式中: f c为混凝土的抗压强度设计值,对于空心构件, f c应乘以1.1; f y 为钢材的抗压强度设计值; A s、 A c为钢管和混凝土的截面面积; α cs 含钢率; θ为套箍系数;B、C为截面形状对套箍效应的影响系数。
规范公式根据“钢管混凝土统一理论”,充分反映了钢管和混凝土两种材料的统一性。然而,规范公式在计算钢管混凝土构件的承载力时,需要分别考虑实心与空心两种情况对相应的参数进行取值,应用较为不便。
1.2 修正计算公式
考虑施工方法对空心钢管混凝土构件组合强度的影响,对混凝土抗压强度调整系数进行修正,提出“等效三向受压区”的假设:等效三向受压区对套箍效应的增强影响较大,根据等效三向受压区的面积占混凝土截面面積的比值,并考虑空心率的影响,提出了套箍系数的修正系数。实心、空心钢管混凝土短柱的轴心受压承载力可按修正公式计算。
式中: A h为空心面积; φ为钢管混凝土构件的空心率,对于实心构件,φ=0;m为空心钢管混凝土套箍系数修正系数;k为混凝土抗压强度调整系数;h为经验系数;θ m为修正后的套箍系数。
与规范公式相比,修正公式的物理意义更加明 确,可直接根据空心率大小进行实、空心钢管混凝土构件的轴压承载力计算,无需单独针对实心与空心两种情况分别计算,更加符合“钢管混凝土统一理论”中实心与空心构件性能的连续性要求。
2 模型误差的参数统计
2.1 空心钢管混凝土构件轴压试验
为针对模型误差的参数统计提供样本数据,进行了19根圆形截面空心钢管混凝土短柱的轴压试验。
2.1.1 试验方法 试验采用500 T液压压力试验机施加轴力,应用DH3816静态应变箱采集应变片读值,YHD-30型位移传感器采集试件的轴向变形,试验装置如图1所示。在试件中部截面的四分点处各粘贴1片横向应变片和纵向应变片,如图2所示,并在构件底部四分点处布置4个位移计。试验时采用分级加载,每级持荷时间为2 min。接近极限荷载时,降低加载速度,并使用计算机连续采集应变读值。
2.1.2 试验现象 试验初期,试件处于弹性阶段,外观没有明显变化;进入弹塑性阶段后,试件中部截面的应变和轴向变形变大,增长速度明显加快,试件外观仍没有很大变化;即将达到极限荷载时,在试件中下部出现微小的鼓起;达到极限荷载之后,荷载开始下降,鼓曲缓慢增长并逐渐向外延伸,最后试件出现环形鼓曲,直到钢管的竖向焊缝被拉裂或轴向压缩变形过大而破坏。
2.1.3 试验结果 由于仅需要圆空心钢管混凝土短柱的轴压承载力作为统计样本,因此,仅对试件的轴压承载力进行统计与分析。文中列出试验中部分圆形截面试件的轴压试验结果,其余试验结果及详细分析可参见文献[13],试验承载力结果如表1所示。
2.2 计算模型误差
在构件抗力计算过程中,当采用的基本假定不完全符合实际或将计算公式进行近似简化时,将引起一定的误差,此误差即为计算模型误差(ME,Model Error),表示为试验实测承载力与规范公式和修正公式计算得到的承载力之间的比值。
ME= 试验收实测承载力[]公式计算承载力 (11)
本文从试验及相关文献中搜集了总计61根圆形截面空心钢管混凝土短柱轴压试验数据作为统计样本,分别采用Normal、Lognormal、Weibull、Gamma分布,对模型误差ME进行数值拟合,分别得到规范公式和修正公式的计算模型误差。如图3~ 图6所示。
根据各分布的概率密度分布曲线与直方图在左 侧下端敏感区域的相对位置,可得出该分布对计算模型误差的估计偏差。由图4可知,规范公式各模型误差的逆累积分布曲线都位于1∶1线上方,高估了可靠度指标,Weibull分布的逆累积分布曲线与1∶ 1线比较接近。由图3可知,Weibull分布的峰值点与直方图的最为接近,因此选取Weibull分布作为规范公式的模型误差的最优分布。由图6可知,修正公式各逆累积分布曲线都位于1∶1线下方,低估了可靠度指标,Gamma分布和Lognormal分布的逆累积分布曲线与1∶1线最为接近。由图5可知,Lognormal分布和Gamma分布的峰值点与直方图比较接近,选用Lognormal分布作为修正公式模型误差的最优分布。
2.3 材料性能误差
材料性能误差是指由于材料本身品质的差异,以及制作工艺、环境条件等因素引起的材料性能的差异。钢管混凝土中不同强度材料的性能统计参数,如表2所示。
2.4 几何参数误差
空心钢管混凝土结构的几何截面图如图7所示。由于制作和安装方面的原因,结构构件的尺寸会出现偏差,制作安装后的实际结构与设计预期的构件几何特征的差异即为几何参数误差。相关的几何参数包括:钢管面积、内填混凝土面积、空心部分面积、含钢率和空心率。其误差的统计参数可按钢结构中的相关参数取用[14] 。
2.5 荷载误差
荷载是随时间变化的随机变量,在数学上可以采用随机过程概率模型来描述。对结构设计来说,最有意义的是结构设计基准期内的荷载最大值,通常将荷载处理成平稳二项随机过程。根据《建筑结构荷载规范》(GB 50009—2012)得到荷载的统计参数,如表4所示。
3 方法与步骤
采用Monte Carlo法[15] 对圆空心钢管混凝土构件进行可靠性分析,该方法通过建立数学模型并随机抽样对结构的可靠性进行模拟,不考虑功能函数的复杂性,回避了结构可靠度分析中的数学困难,因此,对复杂的隐式极限状态函数尤为适用。Monte Carlo法的基本步骤为:
1)根据算例中所选用的空心钢管混凝土试件的各项参数,以及抗力相关变量的分布类型和统计参数,产生抗力的随机数列;
2)将材料强度设计值和原尺寸代入该构件的轴压承载力计算公式,得到构件的承载力设计值,利用荷载效应比计算荷载效应组合,根据荷载的分布类型和统计参数,产生荷载的随机数列;
3)输入模拟次数 N ,为了得到较高精度的结果,取模拟次数为5×107次;
4)将抗力和荷载的随机变量代入功能函数 Z=g(X 1,X 2,X 3,…,X N) 进行计算,统计 Z <0的次数 n ,失效概率为: P f= n/N ;
5)当随机变量为正态分布时,可得到可靠度指标为: β=--1 (P f) 。
4 结果分析
4.1 含钢率的影响
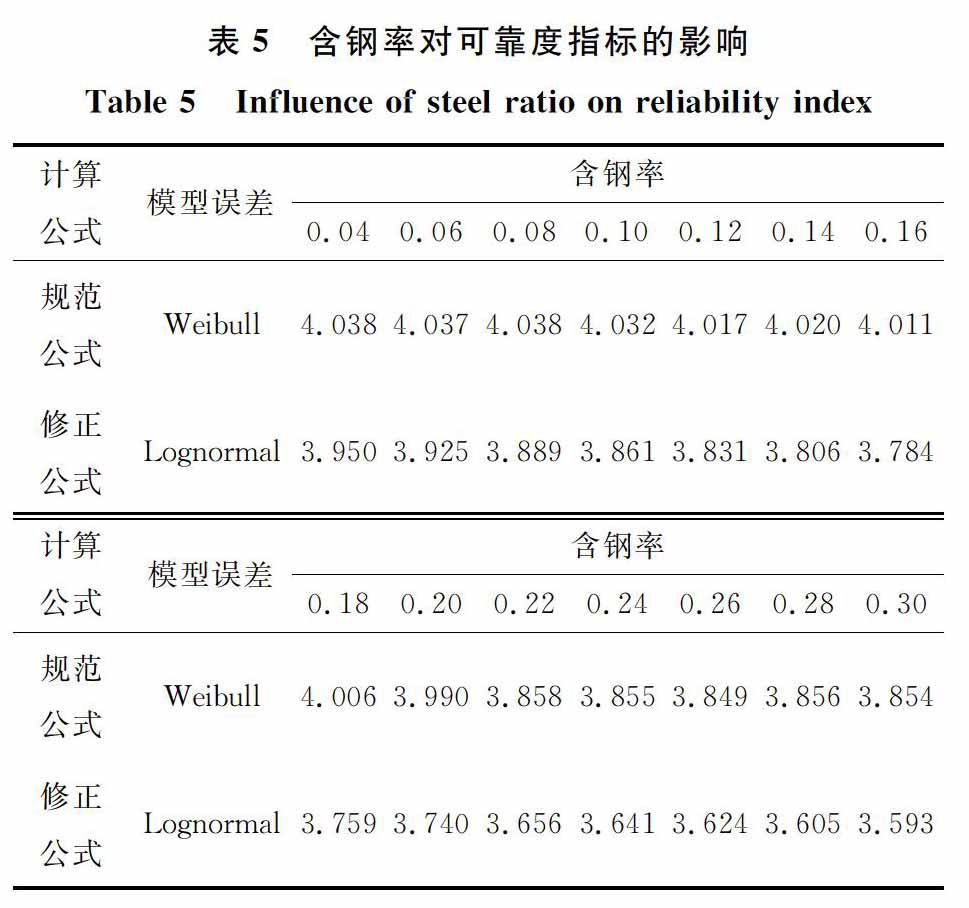
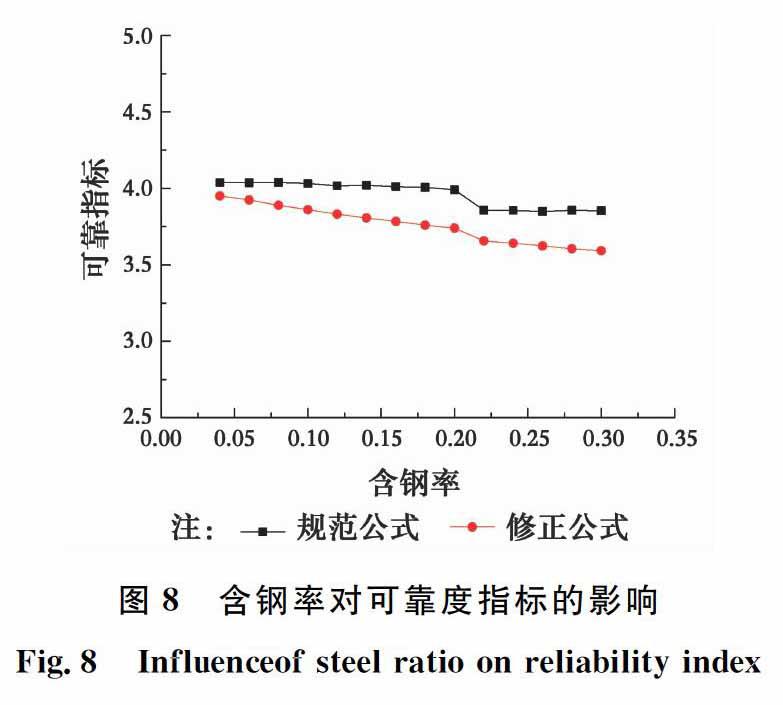
以含钢率为控制参数设计工况14组。活载类型为住宅,试件的钢管直径为300 mm,钢材强度等级为Q235,混凝土强度等级为C50,空心率为0.30,荷载效应比为0.5,钢管厚度为2~14 mm,混凝土外径为149~162 mm,含钢率为0.04~0.30。结果如表5和图8所示。
从图8可知,规范公式和修正公式的可靠度指标均随着含钢率的提高而降低。原因在于當含钢率较高时,试件中钢材含量较高,混凝土含量较低,而钢材强度的均值系数相对于混凝土强度较小,导致可靠度指标较低。
4.2 材料强度的影响
算例分别以混凝土强度和钢材强度为控制参数设计工况12组。活载类型为住宅,试件的钢管直径为300 mm,钢管厚度为5 mm,混凝土外径为159 mm,含钢率为0.10,空心率为0.30,荷载效应比为0.5,混凝土强度等级为C30~C80,钢材强度等级为Q235~Q345。结果如表6和图9所示。 如图9所示,规范公式和修正公式的可靠度指标均随着混凝土强度的提高而上升。这是由于随着混凝土强度等级的提高,混凝土的均值系数虽然减小,但是变异系数也随之减小。当采用相同强度等级的混凝土时,采用Q235钢材的可靠度指标比采用Q345的略大,说明可靠度指标随着试件钢材强度的提高而下降,下降幅度不明显。这是由于Q235钢材和Q345钢材的均值系数和变异系数相差不大,对可靠度指标影响不明显。当混凝土强度较低时,规范公式的可靠度指标较大,当混凝土强度较高时,修正公式的可靠度指标较大。
4.3 空心率的影响
算例以空心率为控制参数设计工况12组。活载类型为住宅,试件的钢管直径为300 mm,钢材强度等级为Q235,混凝土强度等级为C50,含钢率为0.10,荷载效应比为0.5,钢管厚度为3~6 mm,混凝土空心内径为91~238 mm,空心率为0.10~0.65。结果如表7和图10所示:
如图10所示,随着试件空心率的提高,规范公式的可靠度指标的变化曲线呈波动趋势。这是由于规范公式分开实心和空心两种情况,空心率由混凝土面积控制,公式中没有把空心率作为独立参数考虑。变化曲线的波动最小值和最大值之间的差值为0.249,相差6.08%,可认为可靠度指标变化曲线的波动趋势不大,空心率的变化对可靠度指标的影响不大,与“统一理论”中实、空心钢管混凝土构件的连续性要求相符。修正公式的可靠度指标随着空心率的提高呈缓慢上升趋势。最小值和最大值分别为3.645和3.978,两者相差0.333,差值不大。由于空心率误差的平均值为1,标准差较小,试件空心率变化对可靠度指标的影响不大。
4.4 荷载效应比的影响
荷载效应比为活载与恒载的比值,结构设计中根据楼面材料取值。算例以空心率为控制参数设计工况8组。活载类型为住宅,试件的钢管直径为200 mm,钢管厚度为5 mm,含钢率为0.11,混凝土强度等级为C50,钢材强度等级为Q235,荷载效应比为0.25~2。结果如表8和图11所示。 如图11所示,规范公式和修正公式的可靠度指标均随着试件荷载效应比的提高而上升。这是由于随着荷载效应比的提高,试件承受的总荷载中活荷载的比例较大,恒荷载的比例较小,而活荷载的均值系数比恒荷载的小,导致可靠度指标较大。当荷载效应比较小时,曲线上升趋势较快,荷载效应比对可靠度指标的影响较明显,当荷载效应比较大时,曲线上升趋势较平缓,荷载效应的影响较不明显。
5 抗力分项系数
5.1 分项系数的设计表达式
结构可靠度设计一般采用分项系数的设计方法, 该方法能较好地适应设计条件的变化,在确定的分项系数条件下,取得与目标可靠指标较一致的结果。分项系数的设计表达式为
γ S 1 S k 1+γ S 2 S k 2+…+γ S n S k n ≤ 1[]γ R R k (12)
由此可得荷载和抗力的分项系数为:
γ S = (1+δ X S β cos θ S )[]
(1+k S δ X S ) (13)
γ R = (1-k R δ X R )
[](1+δ X R β cos θ R ) (14)
式中: cos θ i=- g[]X i | X* σ X i / ∑ n[]i=1 g[]X i | X*σ X i 2 1/2 。
由分项系数的设计表达式可知,影响抗力分项系数的因素有:抗力误差、荷载误差和目标可靠指标。抗力的统计参数主要与计算模型误差有关;荷载的统计参数主要与活载类型和荷载效应比有关;目标可靠度指标主要与结构的安全等级有关。
5.2 计算模型误差分布类型和活载类型的影响
为分析计算模型误差分布类型和活载类型对抗力分项系数的影响,设计工况结构安全等级为二级,荷载效应比为0.50,对应的恒载分项系数为1.2,活载分项系数为1.4,楼面活载类型分别为办公楼和住宅。计算结果如表9所示。
由表9可知:采用规范公式时,服从4种分布类型的抗力分项系数相似,差值为0.01,相差0.8%;采用修正公式时,服从Lognormal、Gamma分布的抗力分项系数较小,差值为0.04,相差2.9%。因此,可认为计算模型对抗力分项系数的影响不大。所有工况中采用不同的活载类型(办公楼和住宅)时,抗力分项系数相差不大,最大相差1.10%。因此,可认为活载类型对抗力分项系数影响不大。
5.3 安全等级的影响
由于计算模型误差分布类型和活载类型对抗力分项系数的影响不明显,以下分析时均取各计算公式的计算模型误差最优分布类型,活载类型均取住宅。为分析结构安全等级对抗力分项系数的影响,设计工况荷载效应比为0.50,对应的恒载分项系数为1.2,活载分项系数为1.4,结构安全等级为一级~ 三级,对应的目标可靠指标分别为2.7~4.2。计算结果如表10所示。
由表10可知:随着结构安全等级的提高,钢管混凝土构件抗力分项系数的取值提高,每级提高约10%。原因在于随着结构安全等级的提高,目标可靠度指标提高,从结构可靠度分析的角度考虑,提高目标可靠度指标,即提高结构的安全储备,需提高抗力分项系数以减小抗力设计值。
5.4 荷载效应比的影响
为分析荷载效应比对抗力分项系数的影响,设计工况结构安全等级为二级,荷载效应比为0.10~2.0,对应的恒载分项系数为1.35和1.20,活载分项系数为1.40,活载类型为住宅。计算结果如表11和图12所示。
由图12可知,随着荷载效应比的提高,抗力的分项系数有所提高。建筑工程中住宅的楼面荷载效应比常用值为0.5~1.75,在此范围内,规范公式的抗力分项系数差值为0.21,差值比为17.3%;修正公式的差值为0.36,差值比为26.3%。由此可见钢管混凝土结构的抗力分项系数在采用不同荷载效应比时的取值相差较大。
当荷载效应比小于1.00时,曲线上升趋势较快,荷载效应比对抗力分项系数的影响较明显;应根据荷载效应比不同对抗力分项系数进行取值;当荷载效应大于1.00时,曲线上升趋势较平缓,荷载效应比的影响较不明显,取各分项系数的平均值作为抗力分项系数,如表12所示。
如表12所示,荷载效应比提高一级,实心和空心构件的抗力分项系数均增大约10%。当荷载效应比为0~0.50时,修正公式的分项系数比规范公式的大13%;当荷载效应比为0.50~1.00时,修正公式的分项系数比规范公式的大17%;当荷载效应比为1.00以上时,修正公式的分项系数比规范公式的大21%。规范公式的不确定更小。对于空心构件的设计表达式,建议采用规范公式1,当荷载效应比为0~0.50,0.50~1.00,1.00以上时,抗力分项系数分别取1.21、1.32、1.41。空心钢管混凝土轴压构件的设计表达式为
γ 0 (γ G S G k +γ Q 1 S Q 1k +∑ n[]i=2 γ Q i ψ c i S Q ik )≤
1 γ R R k (f k,a k,…) (15)
式中: γ 0為结构重要性系数;γ G为恒载分项系数,当荷载效应对结构不利时,对由活载控制的组合,取1.2;对由恒载控制的组合,取1.35; γ Q i 为第 i 个活载分项系数,一般取1.4;
S G k 為恒载标准值效应; S Q ik 为第 i 个活载标准值效应; ψ c i 为第 i 个活载的组合值系数; γ R为抗力分项系数,考虑不同的抗力计算公式和荷载效应比,按表12取值。
6 结论
1)《钢管混凝土结构技术规范》中给出的圆空心钢管混凝土轴压承载力计算公式及修正公式的可靠指标均随着混凝土强度和荷载效应比的提高而上升,随着含钢率的提高而下降,计算模型误差对可靠指标的影响较大,钢材强度和空心率的变化对可靠度指标的影响不明显。
2)两种公式的可靠指标均能基本满足目标可靠指标3.7的要求,当混凝土强度等级低于C60时,规范公式的可靠度指标较大,约为修正公式的1.05倍,对于空心钢管混凝土短柱的轴压承载力计算,规范公式的计算结果更为可靠。
3)计算模型误差分布类型和活载类型对抗力分项系数的影响不明显;随着结构安全等级的提高,抗力分项系数的提高;荷载效应比对可靠度指标影响较大,规范公式的不确定性更小,当荷载效应比为0~ 0.50、0.50~1.00、大于1.00时,使用规范计算公式进行设计时,抗力分项系数可分别取1.21、1.32、1.41。
参考文献:
[1] 钢管混凝土结构技术规范:GB50936—2014[S]. 北京:中华人民共和国住房和城乡建设部,2014.
Technical code for concrete filled steel tubular structures:GB50936-2014 [S]. Beijing:Housing and urban-rural development of the People's Republic of China,2014.(in Chinese)
[2] 何敏,刘庆文,张亮,等. 梁受弯承载力极限状态的可靠度研究[J]. 南昌航空大学学报(自然科学版)2017,31(1): 36-40.
HE M, LIU Q W, ZHANG L, et al. Reliability analysis for RC beams based on carrying capacity limited state[J]. Journal of Nanchang Hangkong University(Natural Sciences)2017, 31(1): 36-40. (in Chinese)
[3] 袁健,易伟建. 钢筋混凝土梁受剪承载力可靠度分析[J].建筑结构学报,2017,38(4): 109-128.
YUAN J, YI WJ. Reliability analysis of shear capacity of reinforced concrete beams[J]. Journal of Building Structures, 2017, 38(4): 109-128.(in Chinese)
[4] BAJI H, RONAGH H R, MELCHERS R E. Reliability of ductility requirements in concrete design codes [J]. Structural Safety, 2016, 62:76-87.
[5] 潘春宇,童乐为. 钢结构疲劳可靠度设计方法的研究进展[J]. 钢结构,2013,28(12):1-8.
PAN C Y, TONG L W.Research progress of fatiure reliability analysis methods for steel structures [J]. 2013, 28(12):1-8.(in Chinese)
[6] LIU W Y, RASMUSSEN K J R, ZHANG H.Systems reliability for 3D steel frames subject to gravity loads [J]. Structures, 2016,8: 170-182.
[7] BECK A T, OLIVEIRA W L A D, NARDIM S D. Reliability-based evaluation of design code provisions for circular concrete-filled steel columns[J]. Engineering Structures, 2009, 31(10): 2299-2308.
[8] STEWART M G, LAWRENCE S J. Model error, structure reliability and partial safety factors for structural masonry in compression[J]. Masonry International,2007, 20(3):107-16.
[9] ZHAI X M, STEWART M G. Structural reliability analysis of reinforced grouted concrete block masonry walls in compression [J]. Engineering Structrues,2010, 32:106-114.
[10] 査曉雄,张晓伟,万城勇,等. 钢管混凝土构件可靠度分析[J]. 施工技术,2014,43(Sup):367-370.
ZHA X X, ZHANG X W, WAN C Y, et al. Analysis on reliability of concrete filled steel tubular structure[J]. Construction Technology, 2014, 43(Sup): 367-370.(in Chinese)
[11] 余敏,李书磊,王圣松. 钢管混凝土构件轴压承载力设计的可靠度分析[J]. 建筑钢结构进展,2017,4(2):47-52.
YU M, LI S L, WANG S S. Reliability analysis of the bearing capacity of concrete-filled steel tube under axial compression [J]. Progress in Steel Building Structures, 2017, 4(2):47-52.(in Chinese)
[12] 卢德辉. 圆、方形空心钢管混凝土柱抗震性能及设计方法研究[D].广州:广州大学,2012.
LU D H. Research on the seismic behaviors of circular and squareH-CFSTcolumn[D].Guangzhou:Guangzhou University,2012.(in Chinese)
[13] 王宏伟. 空心钢管混凝土构件试验与统一理论研究[D].哈尔滨:哈尔滨工业大学,2008.
WANG H W. Research on unified theory and experimental of hollow concrete filled steel tube[D].Harbin: Harbin Institute of Technology,2008. (in Chinese)
[14] 施刚,朱希. 国产建筑结构用钢板设计指标和可靠度分析[J]. 建筑结构学报,2016,37(3):110-124.
SHI G, ZHU X. Design indexes and reliability analysis of domesticsteel plates for building structures[J]. Journal of Building Structures, 2016, 37(3): 110-124.(in Chinese)
[15] MOHAMED A B, SHEIKHLY M A, LIVINGSTON R. Monte Carlo simulations of a portable prompt gamma system for nondestructive determination of chloride in reinforced concrete [J]. Nuclear Instruments and Methods in Physics Research,2008, 266 (15):3397-3405.

