不同应力路径下旋转硬化方程的统一表示及验证
张浩 吴志鸿 张峰 戴自航


摘 要:在收集到的大量试验数据的基础上,结合旋转硬化表达式,提出一个适用于不同应力路径下的旋转硬化表达式,该公式中共有两个参数,通过理论分析得到这两个参数的确定方法。将该公式导入修正剑桥模型来模拟土体在不同加载路径下的应力 应变行为,将模拟结果与试验结果进行对比,结果显示,采用该旋转硬化表达式的各向异性本构模型得到的结果与试验结果均吻合较好,从而验证了该旋转硬化表达式的合理性。
关键词:旋转硬化;应力路径;统一表示;本构模型
中图分类号:TU411
文献标志码:A 文章编号:1674-4764(2018)06-0039-07
Unified expression and verification of rotational hardening
equations under different stress paths
Zhang Hao1,2 , Wu Zhihong1, Zhang Feng1, Dai Zihang2
(1.Strait Construction and Development Co.,Ltd, Fuzhou 350003, P.R.China;
2.College of Civil Engineering, Fuzhou University, Fuzhou 350116, P.R.China)
Abstract:Based on the collected series of experimental data and many well-known rotational hardening expressions, a rotational hardening expression for different stress paths is proposed, mainly including 2 parameters which can be determined in a direct way through analysis. The proposed rotational hardening expression has been implemented to the MCC model and adopted to represent the stress-strain behavior of clays under different loading paths. The simulations are compared with the experimental results. The comparisons show that the simulated results with this proposed method have good agreement with the experimental results, verifying the rationality of the proposed rotational hardening expression.
Keywords:rotational hardening; stress path; unified expression; constitutive model
原状土体是在一定应力条件下形成的,土体颗粒结构产生定向排列,在宏观结构上形成一定的各向异性。同时,土体的变形与加载应力路径密切相关,采用不同的应力加载路径会得到不同的应变,引起初始各向异性的变化,形成土体颗粒之间的新的排列,这种新的各向异性称为诱发性各向异性。在屈服面模型中,这种各向异性通过屈服面的旋转来表示,这就是模型中采用的旋转硬化表达式。
研究人员对旋转硬化规律采用了不同的表达形式。Wheeler等[1] 提出的旋转硬化表达式同时考虑了塑性体积应变和塑性剪切应变的影响,但旋转硬化参数不能直接确定,需要通过反分析,并且没有考虑洛德角的影响。Whittle等[2] 提出的旋转硬化表达式采用临界状态线作为旋转的边界线,只考虑了塑性剪切应变对旋转硬化的影响,这与试验现象不吻合。Taiebat等[3] 没有考虑塑性剪切应变的影响,同时,参数值不能直接确定,需要通过反分析,屈服面的旋转存在边界线。Zhang等[4] 依据交变加载试验结果提出了一个旋转硬化表达式,该表达式考虑了塑性剪切应变的作用,但是,参数需要通过反分析才能确定,给计算带来不便。Hashiguchi[5] 认为屈服面旋转过程中塑性体积应变没有影响,采用 K 0线作为屈服面的倾斜线,这与已有的试验结果不符。Hueckel等[6] 同时考虑了塑性体积应变和塑性剪切应变对旋转速度的影响,但是,旋转硬化参数的确定缺乏依据。Newson等[7] 采用应力表示屈服面的旋轉速度,屈服面的旋转只考虑了每一步的应力增量,没有考虑剪切应力的作用,同时,由于该本构模型采用非相关联流动法则,使得该旋转硬化表达式非常复杂。王立忠等[8] 提出的表达式同时考虑了塑性体积应变和塑性剪切应变的作用,认为屈服面的旋转存在一定的范围,超过该范围时,对应屈服面的倾 斜角度平衡值为0。对土体旋转硬化规律表达形式方面的研究成果还有很多[9-14] ,目前提出的旋转硬化表达式均是针对某一种具体的应力路径所提出的,当应力路径发生改变时,旋转硬化表达式的适用性有待验证。 基于此,在收集到的试验数据基础上,提出了一个考虑应力路径变化的旋转硬化规律表达式,该表达式包括两个参数,通过理论分析得到了这两个参数的直接确定方法。将该规律导入修正剑桥模型,建立了一个能描述各向异性的本构模型,采用该模型模拟了3种不同应力路径下土体的应力 应变关系,将模拟结果与试验结果进行对比,证明该旋转硬化表达式能适用于不同应力路径。
1 旋转硬化方程的统一表示
1.1 旋转硬化方程的分类
研究人员针对旋转硬化规律采用了不同的表达形式,不同表达形式之间,塑性剪切应变和塑性体积应变对应的平衡值也不相同。依据加载应力比 η 和相对应屈服面的倾斜角度平衡值 α 之间的关系,这些旋转硬化表达式可划分为3种类别。
第1种: η 与 α 之间为线性关系,不存在 旋转极限线,方程式为
α=xη (1)
式中: x 为 η 与 α 之间的线性比例关系参数,其取值一般为1和0,这种关系式比较典型的旋转硬化规律包括Whittle等[2] 、Taiebat等[3] 及Zhang等[4] 提出的旋转硬化表达式。
第2种: η 与 α 之间为线性关系,但是存在旋转极限线,超出旋转范围极限线之后,屈服面对应的倾斜角度平衡值 α 为0,表达式为
α=η η ≤ M- α α=0 η > M- α (2)
这种关系式比较典型的旋转硬化规律包括王立忠等[8] 提出的旋转硬化表达式。
第3种: η 与 α 之间为曲线关系,比较典型的包括Wheeler等[1] 提出的旋转硬化规律表达式。
3 3η-4α M2-η2 =±8β 3α-η η-α (3)
为了分析这3种表达方式的合理性,收集了14种数据的应力比 η/M 和与应力比相对应的平衡值 α/M 之间的试验结果([1], [15-17]) , M 为考虑了洛德角影响的临界状态线的斜率,试验结果与采用这3种表达式进行模拟的结果对比如图1所示。
从图1可以看出,在归一化应力比 η / M 较低的情况下,除了第1种表达式中 x 取0的情况外,依据这3种表达式得到的模拟结果与试验结果之间都吻合得比较好,当 η/M 的值达到一定值之后,塑性剪切应变的影响程度开始增加,随着归一化应力比 η/M 的增加 ,α/M 反而开始下降。采用第2种关系式得到的曲线虽然也能反映出这种趋势,但是模拟曲线与试验结果之间存在明显差距。
1.2 旋转硬化方程的统一表示及参数确定
1.2.1 旋转硬化表达式 从图1可以看出,第3种表达式能较好地反映 α/M 随 η/M 的增加而下降的趋势,但试验结果与模拟结果之间存在一定误差,尤其在拉伸状态下,这种误差比较明显。同时,通过试验数据也可以看出,在应力比 η 较低的情况下,塑性体积应变占主导位置, η 与 α 之间相等,当应力比 η 趋向于 M 时, α 接近于0。基于此,提出旋转硬化规律的统一表达式为
d α=μ aη-α d ε p v -β bη-α d ε p s (4)
式中总共包含4个参数,分别是 μ 、 β 、 a 和 b ,当这4个参数取不同的值时,就可以得到不同的旋转硬化规律表达式。同时,从图1可以看出,在应力比 η / M 较低时, η/M 近似等于 α/M ,当达到一定程度之后, α/M 随着 η/M 的增大逐渐减小,最后趋向于0。为了反映这种趋势,本文提出参数 a 和 b 分别取1和0,得到的旋转硬化规律表达式为
d α=μ η-α d ε p v +βα d ε p s (5)
为验证该旋转硬化方程的合理性,将该表达式嵌入修正剑桥模型,有关修正剑桥模型的具体介绍可参考文献[18] 。建立了一个能描述各向异性的弹塑性本构模型,模型的屈服面方程表示为
f= q-αp - M2-α2 p c -p p=0 (6)
1.2.2 旋转硬化表达式参数的确定
旋转硬化表达式包含两个参数,分别是 μ 和 β ,这里介绍对这两个参数的推导过程。若继续一维压缩过程,屈服面不发生旋转,即
d α=μ η-α d ε p v -βα d ε p s =0 (7)
一维压缩过程中
d ε p s d ε p v = 2 3 d ε 1- d ε 3 dε 1+2 d ε 3 = 2 3 (8)
式中: d ε 1和 d ε 3分別表示压缩过程中的单元体竖向应变和水平应变,联合式(7)和式(8),得到
β= 3 η K 0 -α K 0 2α K 0 (9)
结合方程式(6),一维压缩中塑性体积应变和塑性剪切应变之间的关系表示为
d ε p s d ε p v = f q f p = 2(η K 0 -α K 0 ) M2-η K2 0 = 2 3 (10)
得到
α K 0 = η K2 0 + 3η K 0 -M2 3 (11)
将式(11)代入式(9),可得到
β= 3 η K 0 -α K 0 2α K 0 = 3 M2-η2 K 0 2 η2 K 0 +3η K 0 -M2 (12)
如果将土体式样各向同性固结到先期压力的2~ 3倍左右,则土体的各向异性将基本消失[19] ,此时,发生的塑性体积应变可表示为
ε p v = λ-k 1+e 0 ln p p 0 = λ-k 1+e 0 ln 2~3 ≈ λ-k 1+e 0 (13)
各向同性固结时,应力比 η =0, 塑性剪切应变和塑性体积应变之间的比例关系可表示为
d ε p s d ε p v = f q f p = 2(η-α) M2-η2 = -2α M2 (14)
将式(14)代入式(5),得
1 α 2αβ-M2 d α= μ M2 d ε p v (15)
对式(15)左边积分,得
∫α α 0 1 α 2αβ-M2 d α= 2β M2 ln 2αβ-M2 2αβ α α 0 (16)
假定屈服面累计旋转到初始值 α 0的0.1倍时,土体显示各向同性性质,这样联合式(13)、式(15)和式(16)就可求出参数 μ 的表达式。
μ= 2β 1+e 0 λ-κ ln 10M2-2α 0β M2-2α 0β (17)
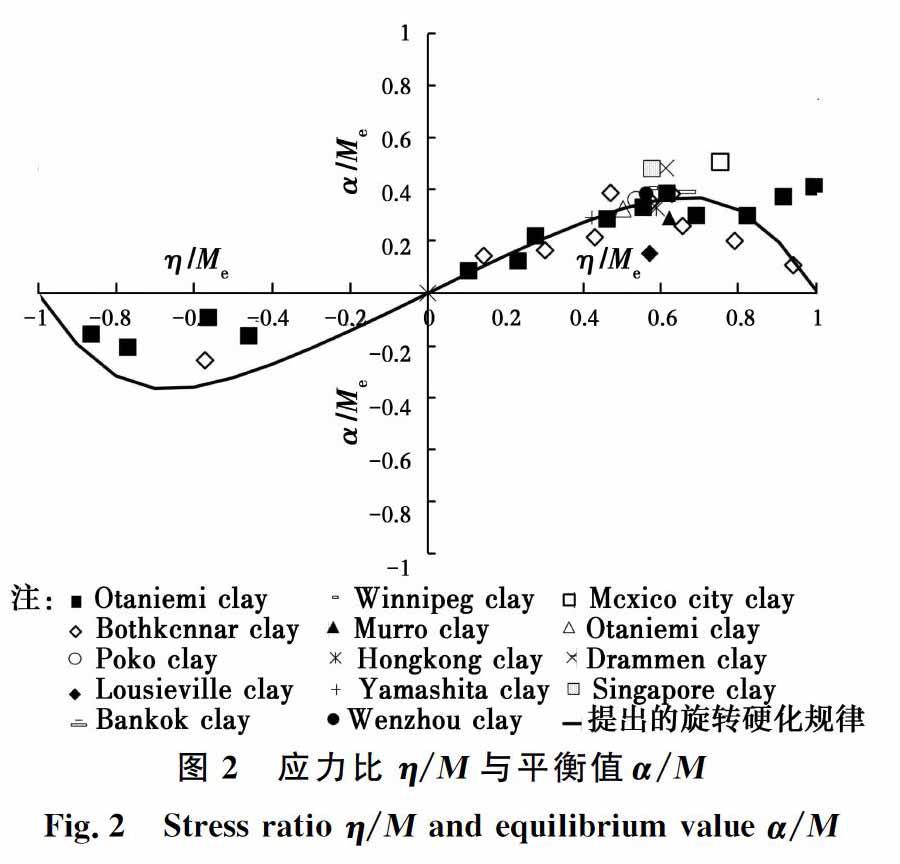
联合式(5)、式(12)和式(17),可建立 α/M 和 η/M 之间的关系曲线,如图2所示。
从图2可以看出,采用本文提出的旋转硬化表达式得到的曲线与试验结果之间吻合得较好,能很好地反映屈服面的倾斜角度先增后减,最后趋向于0的过程。将提出的旋转硬化表达式导入修正剑桥模型,模拟屈服面的旋转以及不同应力路径下的土体试样的应力 应变行为,模型需要输入的模型与修正剑桥模型需要输入的参数相同,总共包含6个,分别为 e 0 、 λ 、 κ 、 M 、 υ 和 p m0 , 参数的物理意义可参考文献[18] 。
2 不同应力路径试验的模拟
为了分析旋转硬化对不同加载路径下土体应力 应变关系的影响,选择3种不同的应力路径进行分析,分别是温州软土三轴排水试验[20] 、BBC(Boston Blue Clay)土的三轴不排水试验[21] 、Otaniemi土的循环加载试验[22] ,这3种土需要输入模型的参数见表1。
2.1 三轴排水试验
沈恺伦[20] 对温州软土进行了三轴排水试验,试验过程先依照原状土的应力状态进行固结,然后再分别进行排水状态下的三轴压缩试验。图3和图4表示的是应力路径为BCD50和BED33时,三轴压缩试验结果和采用不同旋转硬化表达式得到的模拟结果之间的对比。
图3是应力路径为BCD50时试验结果和采用不同旋转硬化表达式时得到的模拟结果之间的对比,从图中可以看出,总体上模拟结果与试验结果之间吻合得比较好,采用不同旋转硬化表达式得到的模拟曲线之间非常接近,在模拟 p - ε v时,随着体积应变的发展,模拟曲线之间开始出现差距。当体积应变达到3%时,模拟曲线之间开始出现一定的差距,与试验结果之间的差距也慢慢增大,在模拟 q - ε s时,采用不同旋转硬化表达式得到的模拟结果与试验结果之间非常接近,都能较准确地模拟 q - ε s的发展趋势。
图4是三轴拉伸试验BED-33时试验结果与模拟结果之间的对比,從图中可以看出,在模拟 p - ε v曲线时,采用不同旋转硬化表达式对模拟结果的影响不是很明显,采用4种旋转硬化表达式得到的模拟曲线之间非常接近,都能较准确地模拟 p - ε v之间的发展趋势,但在模拟 q - ε s曲线时,模拟结果与试验结果存在一定的误差,当剪切应变较小时,模拟曲线之间比较接近,随着剪切应变的发展,模拟曲线之间开始出现一定程度的误差,采用本文提出的旋转硬化表达式得到的模拟结果与试验结果之间吻合较好。
2.2 三轴不排水试验
Ladd等[21] 对BBC(Bonston Blue Clay)土进行了三轴不排水压缩试验,所取土试样首先各向同性固结到150 kPa, 然后根据不同的超固结比值 R oc ,分别卸载到相应的应力值,这里选取的 R oc 分别为1和4,土样在整个加载过程中保持不排水条件,需要输入模型的土体参数见表1。Yu等[23] 也对该试验进行了数值研究。
图5为模拟结果与试验结果之间的对比,从图中可以看出,在对应力路径 p - q 进行模拟时,采用不同旋转硬化表达式得到的模拟曲线与试验曲线之间比较接近,采用这4种旋转硬化表达式都能较准确地反映出 p - q 之间的变化趋势。在模拟 q - ε s时,当OCR为1,即当试样为正常固结时,模拟曲线位于试验曲线的上部,在出现相同的剪切应变 ε s时,模拟得到的剪切应力 q 要大于试验过程中的剪切应力,同时,采用不同旋转硬化表达式得到的模拟曲线之间也不是非常接近,相比较而言,采用本文提出的旋转硬化表达式得到的模拟曲线与试验曲线之间最为接近。当OCR为4时,在模拟应力路径 p - q 时,不同旋转硬化表达式得到的模拟结果与试验结果之间非常接近,都能准确地反映出应力路径 p - q 的变化趋势,在模拟 q - ε s时,模拟结果与试验结果之间存在一定的误差,但这种误差要小于OCR为1时试验结果与模拟结果之间的误差,总体而言,这4个旋转硬化表达式都能较准确地反映出变形趋势,采用本文提出的旋转硬化表达式得到的模拟结果与试验结果之间最为接近。
2.3 循環加载试验
循环加载试验选取Otaniemi重塑土进行了研究,这种土的相关参数及试验过程见Karstunen等[22] 的研究成果,在三轴压缩之前,先将试样按照一定的应力路径 η 0进行固结,随后将试样进行卸载到一定值, 然后对试样进行加载卸载循环试验。本文选取了两组试样,分别是试样CAE3516R和试样CAE3519R,试样CAE3516R模拟结果如图6所示。
从图6可以看出,对于CAE3516R试样,在模拟应力 应变曲线 p - ε v时,采用不同旋转硬化表达式对模拟结果有较大影响。初始加载时,采用Whittle等和王立忠等提出的旋转硬化表达式得到的模拟曲线位于试验曲线的上部,采用本文提出的旋转硬化表达式与Hueckel等提出的旋转硬化表达式得到的模拟曲线之间比较接近。卸载阶段,不同旋转硬化表达式得到的模拟结果之间的差距比加载阶段不同旋转硬化表达式得到的模拟结果之间的差距要明显一些,相比较而言,采用本文提出的旋转硬化表达式得到的模拟结果与试验结果之间更为接近。在模拟应力 应变关系 q - ε s时, 采用4种旋转硬化表达式都能反映出应力 应变关系的变化趋势,但是,相比较应力 应变关系 p - ε v而言,不同旋转硬化表达式得到的模拟曲线之间的差距更明显。
图7为CAE3519R的试验结果与模拟结果之间的对比,从图中可以看出,在模拟应力 应变曲线 p - ε v时,加载阶段,不同旋转硬化表达式得到的模拟结果之间存在一定差距,卸载阶段,不同模拟结果之间则比较吻合。在模拟应力 应变关系 q - ε s时,不同旋转硬化表达式得到的模拟曲线之间差距比较明显,采用本文提出的旋转硬化表达式得到的模拟曲线与实测数据之间最为接近。
3 结论
对提出的旋转硬化规律表达式进行总结,依据加载应力比 η 和相对应屈服面的倾斜角度平衡值 α 之间的关系,将提出的旋转硬化表达式划分为3种类型,分别是线性关系同时不存在旋转极限线、线性关系同时存在旋转极限线以及曲线关系。建立了这3种关系式的函数曲线,函数曲线与试验结果之间的对比结果显示,采用曲线表达形式与试验结果之间最为吻合。
在采用曲线型表达方程的基础上,提出了一个适用于不同应力路径下的旋转硬化表达式,同时考虑了塑性体积应变和塑性剪切应变对旋转速度的影响。表达式共包含两个参数,通过理论分析,得到这两个参数的确定方法。将所提出的旋转硬化表达式导入修正剑桥模型,建立一个能描述各向异性的本构模型,采用此模型模拟了不同应力路径下的应力 应变关系,模拟过程中,同时采用了其他3种旋转硬化表达式。将试验结果与模拟结果之间以及采用不同旋转硬化表达式得到的模拟结果之间进行对比分析,分析结果验证了提出的旋转硬化表达式的合理性。
参考文献:
[1] WHEELER S J, NAATANEN A, KARSTUNEN M, et al. An anisotropic elastoplastic model for soft clay [J]. Canadian Geotechnical Journal, 2003, 40(2):403-418.
[2] WHITTLE A J, KAVVADAS M J. Formulation of MIT-E3 constitutive model for overconsolidated clays [J]. Journal of Geotechnical Engineering, 1994, 120(1):173-198.
[3] TAIEBAT M, DAFALIAS Y F. Simple anisotropic sand plasticity model [J]. International Journal of Numerical and Analytical Methods in Geomechanics, 2008, 32(8):915-948.
[4] ZHANG F, YE B, NODA T, et al. Explanation of cyclic mobility of soils approach by stress-induced anisotropy [J]. Soils and Foundations, 2007, 47(4):635-648.
[5] HASHIGUCHI K. Elastoplastic constitutive equation of soils with the subloading surface and the rotational hardening [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1998, 12(8):197-227.
[6] HUECKEL T, TUTUMLUER E. Modeling of elastic anisotropy due to one-dimensional plastic consolidation of clays [J]. Computers and Geotechnics, 1994, 16(4):311-349.
[7] NEWSON T A, DAVIES C R. A rotational hardening constitutive model for anisotropically consolidated clay [J]. Soils and Foundations, 1996, 36(3):13-20.
[8] 王立忠, 沈恺伦. K 0固结结构性软黏土的旋转硬化规律研究[J].岩土工程学报, 2008, 30(6):863-872.
WANG L Z, SHEN K L. Rotational hardening law of K 0 consolidated structured soft clays [J].Chinese Journal of Geotechnical Engineering, 2008, 30(6):863-872. (in Chinese)
[9] YIN Z Y, YIN J H, HUANG H W.Rate-dependent and long-term yield stress and strength of soft Wenzhou marine clay: experiments and modeling [J]. Marine Georesources and Geotechnology, 2015, 33(1):79-91.
[10] YIN Z Y, WANG J H. A one-dimensional strain-rate based model for soft structured clays [J]. Science in China Series, 2012, 55(1):90-100.
[11] 姚仰平, 张丙印, 朱俊高. 土的基本特性、本构关系及数值模拟研究综述[J]. 土木工程学报,2012, 45(3):128-150.
YAO Y P, ZHANG B Y, ZHU J G. Behaviors, constitutive models and numerical simulation of soils [J].China Civil Engineeing Journal, 2012, 45(3):128-150. (in Chinese)
[12] 杨召焕, 王建华.循环荷载作用下饱和软土的各向异性边界面模型[J].岩土力学,2016, 31(Sup1):63-70.
YANG Z H, WANG J H. Anisotropic bounding surface model for saturated soft clay under cyclic loading [J]. Rock and Soil Mechanics, 2016, 31(Sup1):63-70. (in Chinese)
[13] 褚福永, 朱俊高, 赵颜辉, 等. 粗粒土初始各向异性弹塑性模型[J].中南大学学报,2012,43(5):1914-1919.
ZHU F Y, ZHU J G, ZHAO Y H, et al. An elastoplastic model for granular soil considering initial anisotropy [J]. Journal of Central South University, 2012, 43(5):1914-1919. (in Chinese)
[14] 刘正义.软黏土屈服特性及各向异性屈服面方程研究[D]. 杭州: 浙江大学,2014.
LIU Z Y. Research on the yield behavior and anisotropic yield surface equation of soft clay [D]. Hangzhou: Zhejiang University, 2014. (in Chinese)
[15] KEVIN M. The stress-strain behavior of bothkennar clay [D]. Glasgow: University of Glasgow, 2006.
[16] 但汉波,王立忠.基于弹黏塑性本构模型的旋转硬化规律[J]. 岩石力学与工程学报, 2010, 29(1):184-192.
DAN H B, WANG L Z. Rotational hardening law based on elastoviscoplastic constitutive model [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1):184-192. (in Chinese)
[17] 但汉波. 天然软粘土的流变特性[D]. 杭州: 浙江大学,2009.
DAN H B. Time dependent behavior of natural soft clays [D]. Hangzhou: Zhejiang University, 2009. (in Chinese)
[18] ROSCOE K H, BURLAND J B. On generalized stress strain behavior of wet clay in engineering plasticity [M]. London: Cambridge University Press, 1968.
[19] ANANDARAJAH A, KUGANENTHIRA N, ZHAO D.Variation of fabric anisotropy of kaolinite in triaxial loading [J]. Journal of Geotechnical Engineering, 1996, 122(8):633-640.
[20] 沈愷伦. 软粘土结构性、塑性各向异性及其演化[D]. 杭州: 浙江大学, 2006.
SHEN K L. Degradation of soil structure and anisotropic plasticity evolution of natural clay [D]. Hangzhou: Zhejiang University, 2006.(in Chinese)
[21] LADD C C, VARALLYAY J. The influence of the stress system on the behavior of saturated clays during undrained shear [R]. Research Rep. No. R65-11, Department of Civil Engineering, MIT, Cambridge, MA, 1965.
[22] KARSTUNEN M, KOSKINEN M. Plastic anisotropy of soft reconstituted clays [J]. Canadian Geotechnical Journal, 2008, 45(3): 314-328.
[23] YU C, XU Q, YIN Z Y. Softening response under undrained compression following anisotropic consolidation [J]. Journal of Central South University, 2013, 20(6):1703-1712.

