立式水泵机组轴系摆度形态的试验分析方法

李耀辉，朱双良

(1.云南省水利水电投资有限公司，云南昆明650051； 2.云南水投牛栏江滇池补水工程有限公司，云南昆明650051)

立式水泵机组轴系摆度形态的试验分析方法

李耀辉1，朱双良2

(1.云南省水利水电投资有限公司，云南昆明650051； 2.云南水投牛栏江滇池补水工程有限公司，云南昆明650051)

立轴水泵机组的摆度是反映水泵机组横向振动的主要特征数据。利用泵站水泵机组实测摆度数据，构建立式水泵机组轴系摆度形态参数模型，采用几何分解计算和分析方法，定义水泵转轮段和电动机段的轴系变形形态，进而定义了轴系摆度的4种基本形态。以牛栏江-干河泵站1号水泵摆度测量数据为例，对轴系摆度形态的计算方法给出了详细的计算说明。结果表明，上述轴系形态试验计算方法能直观的反映水泵轴系的变形，为轴系振动分析提供更有效的分析手段。

立轴水泵；轴系；摆度形态；测试数据

0 引 言

水泵机组的振动是影响泵组运行稳定和运行安全的主要因素。影响水泵运行稳定性的水力、电气、机械等诸多因素，最终大多以振动形式反映出来。对于大型立式水泵机组，振动的表现形式主要反映在轴系的振动上。因此，在大型立式水泵机组中一般都配置了轴系振动和摆度监测装置[1-3]，水泵机组振动的分析都是以轴系振动测试为基础进行的[4- 6]。

以轴系摆度数据为核心的振动分析已发展出多种方法，如根据轴心轨迹提取振动特征模糊评判[7]、小波算法[8]、神经网络算法[9]等。此外，随着计算技术的发展，利用有限元方法对轴系进行建模计算也取得了许多有效的成果。另一方面，轴系摆度形态(或轴系几何变形)是轴系振动最直观的表现形式，也是水泵机组安装和调整中最直接的依据[10-12]。因此，将轴系及其支撑结构进行简化，建立轴系的集中参数模型[13]，研究轴系摆度形态的具有工程应用价值。

本文利用泵站水泵机组实测摆度数据，构建立式水泵机组轴系摆度形态，对轴系集中参数建模、摆度形态定义、计算等问题进行了讨论和分析。以牛栏江-干河泵站1号水泵机组无水调试的实测数据为例，对轴系摆度形态的相关计算问题进行了说明。

1 轴系摆度形态

为获取轴系摆度的基本特征，将立式水泵机组轴系简化为图1所示的二圆盘三支承结构模型。

图1 水泵机组轴系结构

图1中，B1、O1、B2、B3、O2分别为上导轴承、电动机转子、下导轴承、水导轴承及水泵转轮的几何形心。r2、r2分别是电动机转子、水泵转轮的径向位移，r3、r4、r5分别是机组大轴在上导、下导、水导轴承处的径向位移。

对于已安装运行的水泵机组，电动机转子和水泵转轮的横向摆度测试困难。实际测量中可通过测量上导轴承、下导轴承、水导轴承处的摆度，间接计算电动机转子和水泵转轮的横向摆度。

利用上导轴承、下导轴承、水导轴承处测试的摆度数据，定义以下4个摆度计算公式

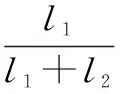
(1)

(2)

(3)

(4)

式中，下标“34”表示采用上导轴承和下导轴承摆度进行换算；下标“35”表示采用上导和水导摆度进行换算。

从图1的结构来看，电动机转子上下均有轴承支撑，电动机转子相对于上下支撑轴承的相对摆动只可能出现外凸和内凹两种基本形式，如图2中的曲线①和②所示。对于水泵转轮，转轮上部有水导轴承支撑，转轮下部近似为自由端，水泵转轮的摆动形态也有两种基本形式，如图2中的曲线③和④。转子根据上述电动机转子和水泵转子的摆度计算值，绘制出在电动机转子形心r1处和水泵转轮r2处轴系的弯曲情况，如图2所示。

图2 转子和转轮摆动基本形态

根据r1和r2处轴系弯曲形态，可组合得到4种可能的轴系摆度型式如表1所示。

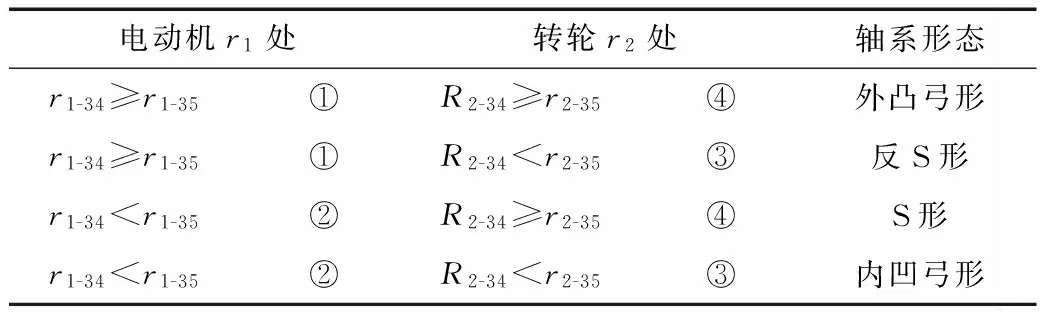
表1 轴系形态类型

上述4种定义的摆度形态，仅仅是从数学角度进行得到的。对于实际运行的立轴水泵机组是否会出现四种形态的轴系摆度，应该与轴系几何结构有关。

2 实例计算

本文以牛栏江-干河泵站1号水泵机组无水启动试验实测数据为例，对轴系摆度形态进行分析计算。

水泵机组轴系结构参数为：l1=1.421 m，l2=1.402 m，l3=3.700 m，l4=1.000 m。1号水泵机组在启动试验中，在10个转速点测试得到的摆度数据见表2。

从表2的数据看，测点X方向和Y方向数据趋势基本一致，如下导X方向摆动幅度小于Y方向摆动幅度。X方向和Y方向的摆动幅度不同，表明轴心轨迹呈椭圆形。本文研究的重点在于轴系的整体摆度形态，X方向和Y方向的摆度数据趋势一致，数据相对偏差不大，不会影响轴系的整体摆度形态。因此，在本文中忽略轴系摆度沿圆周的不均匀性，各测点近似按摆度圆处理，统一采用X方向的摆度数据作为对应测点的摆度圆半径。

表2 1号泵组首次启动摆度数据

根据表2的测试数据，根据公式(1)～(4)计算得到电动机转子和水泵转轮摆度园半径r1、r2的几何计算值，结果列于表3。

表3 转子和转轮摆度圆半径几何计算值

各测点摆度圆半径随转速变化趋势如图3所示。

图3 不同转速摆度变化

从表3和图2中看出，在不同转速下，r1_34大于r1_35，在电动机转子处属于典型的①型摆度曲线；r2-34大于r2-35，在水泵转轮处属于典型的④型曲线。对照表1的形态组合，可知水泵机组轴系为典型的外凸弓形回转。

3 轴系回转形态的重构

按照公式(1)～(4)计算得到的电动机转子形心半径r1_34、r1_35，水泵水泵转轮形心半径r2_34、r2_35是按照相似三角形原理进行换算得到的，即假定r1-r5是线性变化的。实际上，根据第2节的分析，轴系为弓形回转。因此，根据r3、r4、r53点数据采用曲线拟合方式得到轴系回转曲线，并近似得到电动机转子和水泵转轮形心摆度值。

从表3和图3可以看出，在转速较低时摆动幅度较大。摆动幅度大，采用多项式拟合方法进行拟合，不同的拟合阶次可能造成曲线拟合误差大。因此，选取转速n=120 r/min的数据进行试算，确定曲线拟合阶次。

采用2次、3次、4次、5次多项式拟合，轴系摆度曲线如图4所示。

图4 多项式拟合阶次的影响

从图4中可以看出，多项式拟合阶次对轴线摆度形态的影响很大。综合分析后，我们认为采用3次多项式拟合得到的曲线更合理一些。因此，确定采用3次多项式进行拟合计算。

给出不同转速下轴系横向振动形态如5图所示。

根据获得的拟合曲线，通过插值计算得到电动机转子和水泵转轮的摆度数据，如表4。

水泵机组轴线上的关键节点3个导轴承、电动机转子、水泵转轮共5个关键节点，其摆度圆半径随泵组转速变化如图6所示。

图6给出了3个支撑结构(上导轴承、下导轴承、水导轴承)与转动单元(电动机转子、水泵转轮)之间的关系。

图5和图6结合，给出的了轴系摆度形态的完整描述，为分析水泵机组轴系特性和振动问题奠定了理论基础。

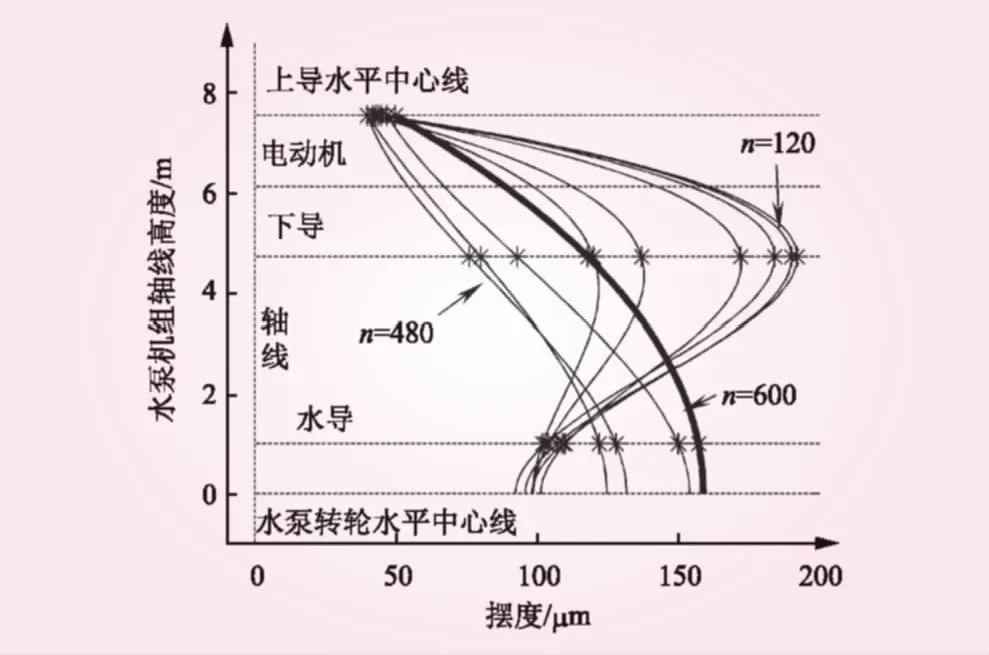
图5 不同转速下轴线摆度形态变化

测点转速n/r·min-1电动机转子r1/μm水泵转轮r2/μm160158.7198.162120160.8395.763180154.3292.294240142.57101.285300112.6798.68636098.6198.46742059.10124.72848054.48131.70954067.30153.891060088.64158.74

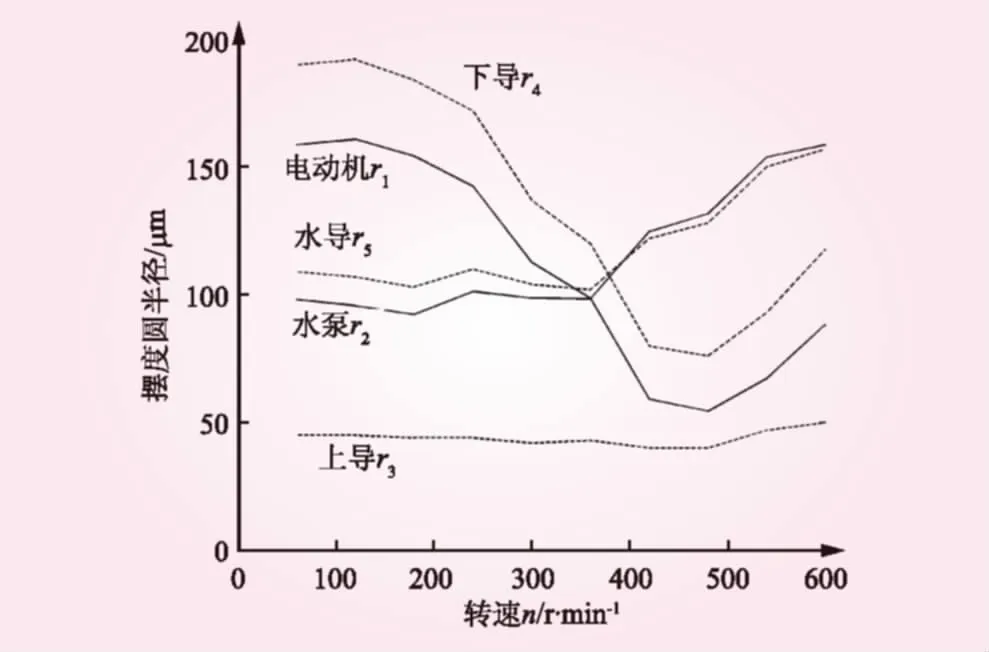
图6 轴线关键节点摆度圆半径随转速变化

作为轴系分析的示例，结合图5、6，可直接得到以下几点结论：

(1)电动机摆度随水泵机组转速增大而逐渐减小、在接近额定转速时，电动机摆度随转速增加而略有增加。

(2)水泵转轮的摆度随水泵机组转速增加而增加，而且其摆度与水导轴承摆度趋势完全一致。主要原因是由于在无水试验中，转轮下部无外力作用，相当于自由端，这种摆度变化符合实际情况。

(3)从图5的轴系摆度形态来看，在机组转速n=600 r/min时，轴系呈外凸弓形，表明下导和水导支撑刚度偏小。进一步地，从图5和图6来看，在不同机组转速下，在下导支撑处的摆度圆半径变化较大，可以认为下导轴承支撑刚度偏小。

在本例计算中采用的干河泵站1号机组，其轴系振动测试数据是达到国家相关标准要求的。上述分析仅仅是结合轴系形态计算结果进行的直观分析，仅仅是为了说明，根据轴系形态变化，可获取轴系振动特性。

4 结 语

本文采用实测数据，构建立轴水泵机组的轴系摆度形态，并给出了详细的计算说明和步骤，为水泵机组的振动分析提供直观的参考。实例计算表明，本文给出的轴系摆度形态描述方法是有效的，在一定程度上能反映轴系支撑系统的动力学特性。

[1] 丁军, 杨小令, 储训. 大型泵站机组振动监测与故障诊断研究[J]. 水泵技术, 2004(2): 41- 43．

[2] 郝春明, 韩骏, 刘红伟, 等. 常熟水利枢纽泵站水泵机组振动监测研究[J]. 水利与建筑工程学报, 2012, 10(3)： 92- 95, 100．

[3] 李斌, 郑源, 徐瑛丽. 大中型泵站机组特性测试与诊断系统研究[J]. 中国农村水利水电, 2012(8): 158- 161, 164．

[4] 陈作义, 潘卫锋, 梁金栋. 大型泵站机组振动测试方法[J]. 排灌机械, 2007, 25(5)： 29- 32．

[5] 佟晨光, 郑源. 大型泵站主机组振动测试与分析[J]. 水泵技术, 2008(2): 12- 15．

[6] 李伟, 季磊磊, 施卫东, 等. 混流泵启动过程转子轴心轨迹的试验研究[J]. 机械工程学报, 2016, 52(22)： 168- 177．

[7] 杨开明, 张建强, 杨小林, 等. 基于模糊综合评判法的泵站机组振动分析[J]. 农业机械工程学报, 2006, 37(11)： 198- 200．

[8] 潘虹, 郑源, 于洋. 基于小波包的泵站机组振动信号特征分析[J]. 水电能源科学, 2007, 25(6)： 109- 112．

[9] 陈坚, 叶渊杰, 陈抒, 等. 基于不变矩和神经网络的泵机组轴心轨迹自动识别[J]. 排灌机械工程学报, 2011, 29(1)： 67- 71．

[10] 仇宝云. 大型立式泵机组轴线摆度的分析与处理[J]. 大电机技术, 1994(6): 7- 11．

[11] 孙志强. 大型泵组轴线摆度的调校方法研究[J]. 广东水利水电, 2015(2): 61- 64．

[12] 杨璋. 三轴承支承主泵振动特性研究[J]. 核动力工程, 2015, 36(3)： 84- 87．

[13] ZENG Yun, ZHANG Lixiang, GUO Yakun, et al. The generalized Hamiltonian model for the shafting transient analysis of the hydro turbine generating sets[J]. Nonlinear Dynamics, 2014, 76(4)： 1921- 1933．

ExperimentalAnalysisMethodofShaftingThrowShapeforVerticalPumpingUnits

LI Yaohui1, ZHU Shuangliang2

(1. Yunnan Water & Hydropower Investment Co., Ltd., Kunming 650051, Yunnan, China; 2. Yunnan Water Conservancy and Hydropower Investment Niulan River to Dianchi Lake Water Diversion Project Co., Ltd., Kunming 650051, Yunnan, China)

The shafting throw of vertical pumping units is main characteristics data that reflect the lateral vibration of water pumping units. The lumped parameter model of shafting of vertical pumping units is established based on on-site measurement throw data of pumping units. By using geometry decomposition and calculation methods, the deformation shapes of water pump shaft section and electromotor shaft section are defined respectively and then four basic shapes of shafting throw are defined. Based on the measurement data of No.1 pumping unit in Niulanjiang-Ganhe Pump Station, the calculation steps and method of shafting throw shape are presented. The results show that the proposed method can visually reflect the deformation of water pump shafting, and provide more valid analysis tool for shafting vibration．

vertical pumping unit; shafting; throw shape; test data

TK72

A

0559- 9342(2017)09- 0077- 04

2017- 01- 23

李耀辉(1960—)，男, 云南德宏人, 副总工程师, 硕士生导师,研究方向为水力机械稳定运行与故障分析．

(责任编辑高 瑜)