高地温引水隧洞围岩与喷层结构热力学参数敏感性分析

姜海波，吴 鹏，张 军

(1.石河子大学水利建筑工程学院，新疆石河子832000；2.新疆维吾尔自治区水利水电勘测设计研究院，新疆乌鲁木齐830000)

高地温引水隧洞围岩与喷层结构热力学参数敏感性分析

姜海波1，吴 鹏2，张 军2

(1.石河子大学水利建筑工程学院，新疆石河子832000；2.新疆维吾尔自治区水利水电勘测设计研究院，新疆乌鲁木齐830000)

以新疆某水电站引水隧洞高地温段为研究对象，以现场监测获得的环向应力、温度数据为基础，对围岩和喷层结构的热力学参数(导热系数、比热、对流系数和线膨胀系数)与喷层环向应力的关系进行了分析，并采用参数敏感性分析法，研究围岩与喷层热力学参数对喷层应力的敏感性。结果表明，围岩和喷层的热力学参数对喷层拱顶环向应力的敏感度排序为：喷层线膨胀系数>喷层导热系数>围岩的导热系数>对流系数>围岩的线膨胀系数>围岩的比热>喷层的比热，拱顶环向应力对喷层线膨胀系数、喷层导热系数、围岩导热系数、对流系数比较敏感，而对围岩线膨胀系数、围岩比热和喷层比热不敏感。

引水隧洞；围岩热力学参数；围岩温度；环向应力；敏感性分析

0 引 言

在围岩开挖、支护结构的设计中，参数的敏感性分析作为系统研究围岩稳定、支护结构力学特性的重要方法，逐步引入到岩土工程领域并得到了广泛的应用[1]。在高地温条件下，围岩及其支护结构的力学特性具有很大的时空变异性，究其原因，其本质是围岩及其支护结构热力学参数的敏感性问题[2-3]。热力学参数随温度、局部地质构造等因素的变化，直接影响着地下工程围岩的稳定性。在实际工程中，若能分析出各参数的敏感性和影响程度，有选择地对高敏感性热力学参数予以精确测定，抓住主要参数，使热力学参数的确定更为有的放矢，同时也为洞室整体布局和支护结构设计提供依据。

目前，获取岩体、支护结构有效热力学参数的主要途径是采用等效概化的方法，结合现场参数信息的反分析进行的[4- 6]。朱维申和何满潮[7]提出了敏感性分析方法，对影响围岩稳定的一系列参数进行了单因素敏感性分析。黄书岭等[8]提出基于敏感度熵权的属性识别综合评价模型，为参数敏感性分析提供了一种新的思路。李晓静等[9]以琅琊山抽水蓄能电站地下厂房为工程背景，选取对地下洞室稳定性影响较为重要的4个参数(变形模量、洞室埋深、主厂房高度、侧压力系数)进行大量塑性数值模拟分析并对位移进行了参数敏感性分析。侯哲生等[10]利用非线性弹塑性有限元法，研究了金川二矿区某巷道围岩力学参数对变形的敏感性，得到了不同参数对变形的敏感性。聂卫平等[11]采用基于弹塑性有限元的洞室稳定性参数敏感性灰关联分析法，对地下洞室稳定影响参数进行了敏感性分析。

前人的研究成果主要集中在围岩力学参数的敏感性分析及其可能出现的变化对围岩稳定、变形的影响程度上。工程实践表明，地下工程的深埋地段存在如高地温、渗透水流等，影响岩体稳定、支护结构力学特性的参数较多，由有限的信息求解众多参数的敏感性问题仍存在一定的困难。以往的研究成果都是通过类比和经验等方法确定力学参数的取值范围[12-14]，并对其进行敏感性分析。地下洞室围岩及其支护结构的热力学参数是数值模拟分析的基础，常温时材料的热力学参数变化很小，一般可以认为是常数，但温度较高时会发生明显的变化，从而影响围岩和支护结构的应力及其稳定性。因此，开展围岩和支护结构热力学参数的变化对其应力的敏感性研究具有极其重要的现实意义。

1 热力学参数敏感性分析

热力学参数的敏感性分析是为了得到参数随温度变化时对喷层应力和温度的敏感性的大小。因应力场和温度场耦合的复杂性，难以求得喷层和围岩应力的显示表达式，故本文采用ABAQUS有限元程序计算喷层的温度场和应力场，结合新疆某水电站引水隧洞工程，选取拱顶、拱肩和侧墙中部的环向应力，对热力学参数的敏感性进行分析。

1.1 工程概况

新疆某水电站引水隧洞为城门洞形，宽4.60 m，高5.23 m，直墙高3.78 m，拱顶半径2.55 m。引水隧洞示意见图1。引水隧洞围岩岩石较坚硬，呈中厚层状，围岩类别为Ⅲ类。引水隧洞施工过程中存在高地温问题，围岩开挖最高温度105 ℃，而运行时的温度低至0～5 ℃，围岩稳定和支护结构的设计受到温度场和应力场耦合的影响。为研究围岩与支护结构热力学参数的变化对应力的敏感性，本文以引水隧洞高地温段围岩热力学参数对围岩喷层环向应力的敏感性分析作为依据，结合现场监测数据，重点分析导热系数、比热、对流系数和线膨胀系数随温度变化时对支护结构应力的敏感性，明确不同参数对支护结构应力的影响程度。

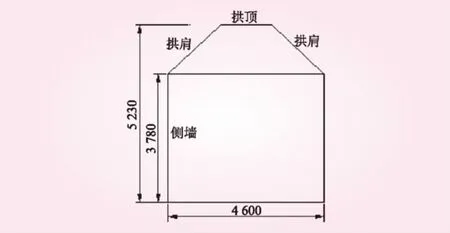
图1 引水隧洞示意(单位：mm)

1.2 敏感性分析方法

敏感性分析首先是建立敏感分析的系统模型，即系统特性P与各因素(a1，a2，…，an)之间的函数关系P=f(a1，a2，…，an)。这种函数关系，尽可能用解析式表示。

建立系统模型后，根据所要讨论的具体问题给出基准参数集。如果要分析某地下洞室围岩应力对其岩石热力学参数变化的敏感性，则该工程岩石热力学参数的推荐值可取为基准参数集。基准参数集确定后，就可对各参数进行敏感性分析。分析参数a*对系统特性的影响时，可令其他各参数取基准值且固定不变，而令a*在其可能的范围内变化，则系统特性P表现为

=φk(ak)

(1)

利用式(1)绘制出系统特性P与参数ak关系曲线，通过P-ak曲线可大致了解系统特性P对参数ak变化的敏感性。

在实际系统中，决定系统特性的各参数往往是不同的物理量，凭借以上的分析，无法对各参数之间的敏感程度进行比较。因此，有必要对各参数进行无量纲化的处理[15]，即将系统特性P*的相对误差δPk=|ΔPk|/P*与参数a*的相对误差δak=|Δak|/a*的比值定义为参数ak的敏感函数Sk(ak)，即

(2)

在|Δak|/a*较小的情况下，Sk(ak)可近似地表示为

(3)

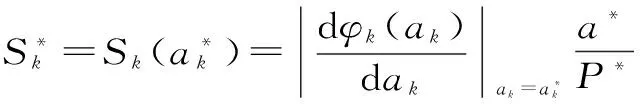
(4)

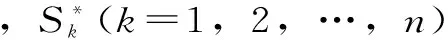
表1 敏感性分析方案及其参数

注：参数计算中，围岩线膨胀系数的第1次取值为0.5×10-6/℃；第2次取值为1.0×10/℃；其他均为2×10-6/℃。

1.3 参与敏感性分析的参数及其分析方案

由于高地温引水隧洞围岩和支护结构材料及受力的复杂性，在计算中所涉及到的参数比较多，不仅包括力学参数(弹性模量、泊松比、线膨胀系数等)，还包括热学参数(导热系数、比热、对流系数等)。从隧洞工程的设计与支护结构的设计出发，分析重要的敏感参数是非常重要的。通过对热力学参数如线膨胀系数、导热系数、比热、对流系数等进行敏感性分析，从而确定出重要的敏感性的参数，为洞室的稳定性分析和支护结构设计提供依据。表1给出了敏感性分析方案及其参数，计算步数表示对某参数进行敏感性分析时，其他参数保持初值不变，在此参数的变化范围内，按其所设计的步长分析所需的计算次数。

2 敏感性分析

2.1 线膨胀系数

2.1.1 围岩

根据表1方案，仅改变围岩线膨胀系数，其他参数均采用初始值进行计算。由于改变的是围岩的线膨胀系数，对温度场没有影响，喷层的温度不随围岩线膨胀系数的改变而改变，所以围岩喷层的温度根据现场实测值(内侧6.4 ℃，外侧31.7 ℃)进行分析，而喷层的应力是随围岩线膨胀系数的变化而变化的，从而可分析围岩线膨胀系数变化时喷层不同部位应力的敏感性。

首先采用上述敏感性分析方法得出敏感度函数，由围岩线膨胀系数和喷层环向应力的关系曲线采用曲线拟合的方法，建立喷层拱顶环向应力σ与线膨胀系数a的函数关系为：σ=0.083 6α+5.24，可得喷层拱顶环向应力敏感度函数Sα为

Sα=(0.083 6α)/(0.083 6α+5.24)

(5)

综上分析，可得围岩线膨胀系数变化时喷层拱顶、拱肩、侧墙中部环向应力的变化情况，并可以分析得出围岩线膨胀系数变化时喷层不同部位应力的变化及其与敏感性的关系。不同围岩线膨胀系数时喷层应力见图2。

图2 不同围岩线膨胀系数时喷层应力变化

从图2可知，围岩线膨胀系数从0.5×10-6/℃提高到10.0×10-6/℃，增大了20倍，喷层拱顶的环向应力从5.37 MPa增大到5.85 MPa，增大了8.94%；喷层拱肩的环向应力从3.1 MPa减小到2.96 MPa，减小了4.5%；喷层侧墙中部的环向应力从1.42 MPa减小到0.82 MPa，减小了40.14%。随着围岩线膨胀系数的增大，喷层拱顶环向应力呈现出线性增加的趋势，拱肩、侧墙中部环向应力都呈现出线性减小的趋势。

从敏感性分析可以得出，随着围岩线膨胀系数的增大，喷层拱顶、拱肩、侧墙中部环向应力敏感度都呈现线性增加的趋势，这说明随着围岩线膨胀系数在0.5×10-6～10.0×10-6/℃范围内增大时，喷层环向应力越来越敏感。

2.1.2 喷层

根据表1敏感性分析方案设计，仅改变喷层线膨胀系数，其他参数均采用初值进行计算。由于改变的是喷层的线膨胀系数，对温度场没有影响，喷层的温度不随喷层线膨胀系数的改变而改变，所以喷层的温度根据现场实测值(内侧6.4 ℃，外侧31.7 ℃)进行分析，而喷层的应力是随喷层线膨胀系数的变化而变化的，从而可分析喷层线膨胀系数变化时喷层不同部位应力的敏感性。不同喷层线膨胀系数时喷层应力见图3。

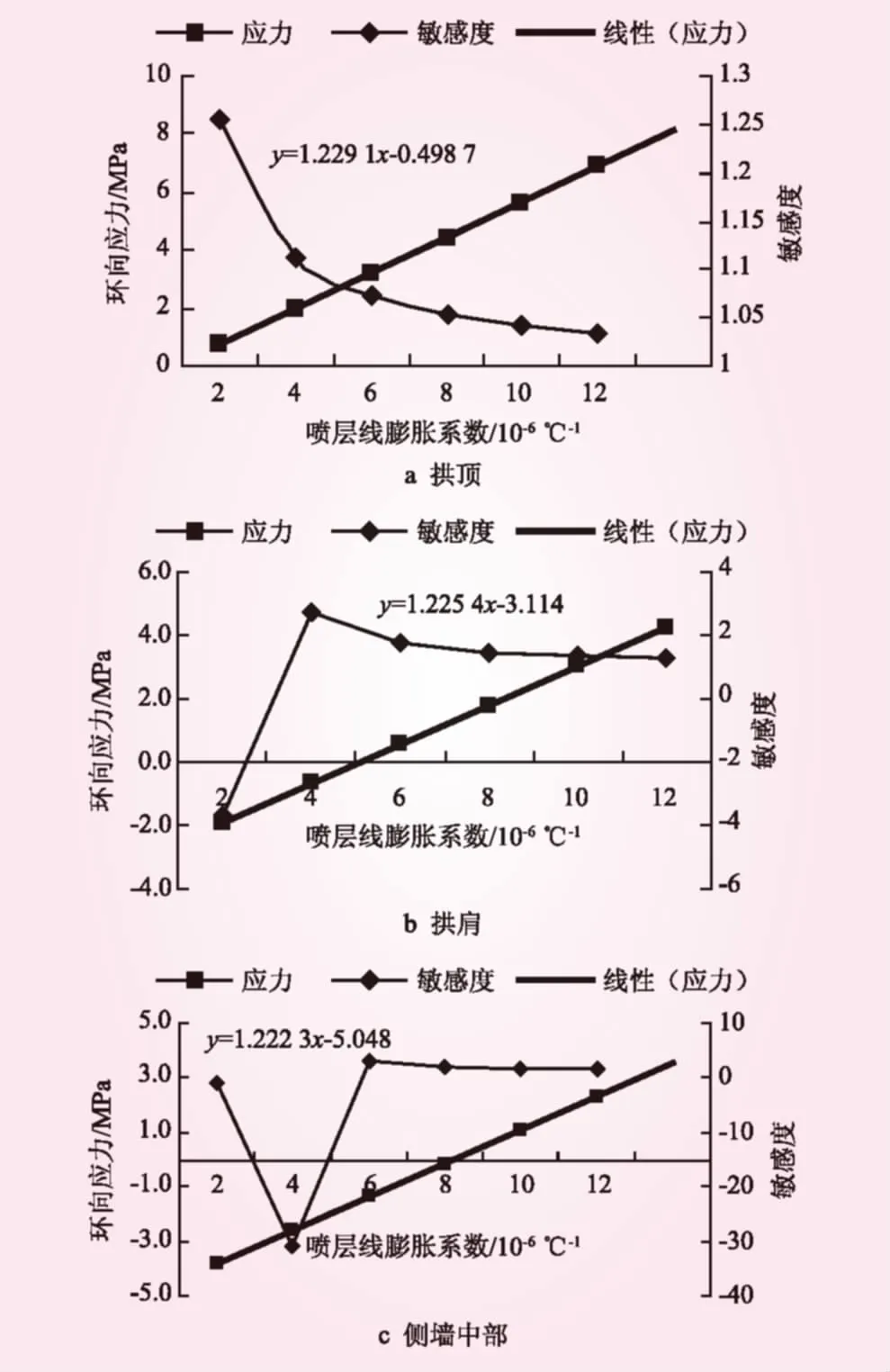
图3 不同喷层线膨胀系数时喷层应力变化

从图3可知，喷层线膨胀系数从2.0×10-6/℃提高到12.0×10-6/℃，增大了6倍，拱顶的环向应力从0.72 MPa增大到6.87 MPa，增大了8.54倍；拱肩的环向应力从-1.89 MPa增大到4.23 MPa，由压应力变为拉应力；侧墙中部的环向应力从-3.82 MPa 增大到2.29 MPa，由压应力变为拉应力。随着喷层线膨胀系数的增大，喷层拱顶、拱肩、侧墙中部环向应力都呈现出线性增加的趋势。

从敏感性分析可以得出，随着喷层线膨胀系数的增大，喷层拱顶环向应力敏感性呈现减小的趋势，且减小幅度越来越小，逐步趋于稳定；喷层拱肩、侧墙中部喷层环向应力敏感性在压应力变为拉应力时出现突变。

2.2 导热系数

2.2.1 围岩导热系数

2.2.1.1温度

围岩导热系数不同时喷层内外侧温度变化见图4。从图4可知，随着围岩导热系数的增加，喷层的内外侧的温度都呈现上升的趋势，这是由于围岩导热系数越大，围岩传导热系数的能力越强，喷层在过水时散热能力就相对降低，所以喷层的温度就会增大。围岩导热系数从5 W/(m·℃)升为30 W/(m·℃)，升高了6倍，喷层内侧温度从6.3 ℃升为7.6 ℃，升高了20.6%；喷层外侧温度从30.1 ℃升高到55.3 ℃，升高了83.72%。可以看出，喷层外侧的温度变化远远大于内侧，主要是喷层内侧直接过水的结果。

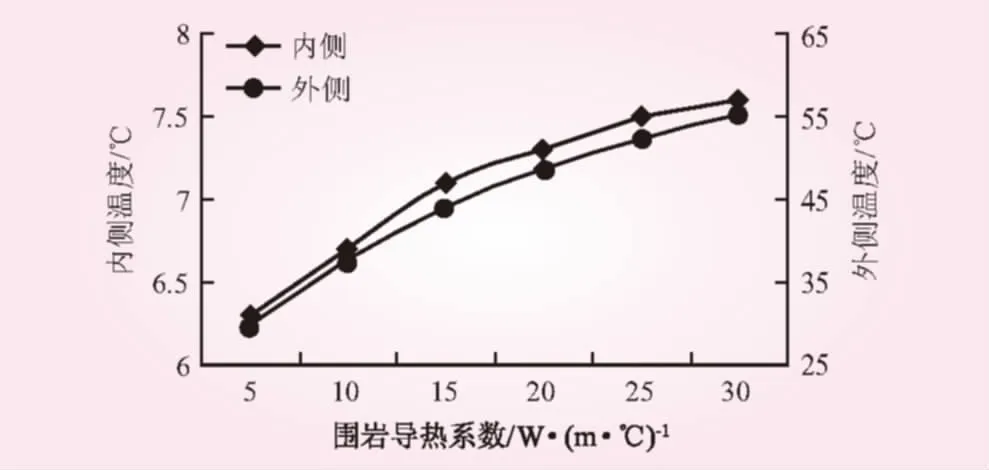
图4 不同围岩导热系数喷层温度变化

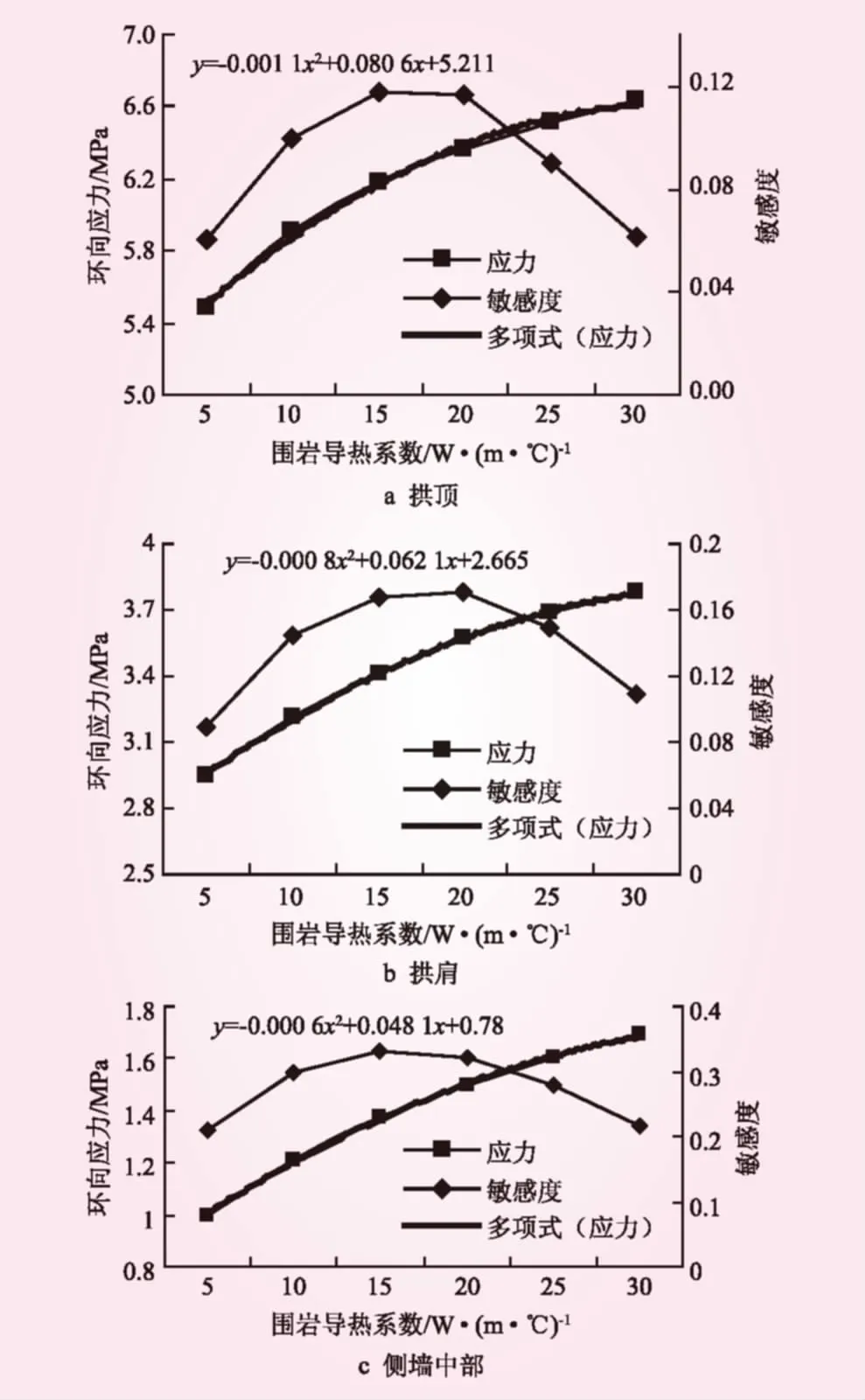
图5 不同围岩导热系数时喷层应力变化

2.2.1.2应力

在上述温度分布下，喷层的应力变化见图5。围岩导热系数从5 W/(m·℃)升到30 W/(m·℃)，增大了6倍，喷层拱顶的环向应力从5.48 MPa增大到6.63 MPa，增大了20.98%；喷层拱肩的环向应力从2.95 MPa增大到3.78 MPa，增大了28.14%；喷层侧墙中部的环向应力从1 MPa增大到1.69 MPa，增大了69%。喷层拱顶环向应力随着围岩导热系数的增大呈现增加的趋势，开始呈线性增加，幅度较大，后来慢慢趋于平缓，呈现出抛物线的形式，先增大后减小；喷层拱肩和侧墙中部的规律和拱顶相似。

2.2.2 喷层导热系数

2.2.2.1温度

喷层导热系数不同时喷层内外侧温度变化见图6。从图6可知，随着喷层导热系数的增加，喷层的外侧的温度呈现降低的趋势，这是由于喷层导热系数越大，喷层传导热系数的能力越强。当喷层的导热系数很低时，就相当于一个隔热层，喷层外侧的温度就会很高，所以喷层外侧温度随着喷层导热系数的增大而降低；对于喷层内侧，由于喷层导热系数的增加，能更好地把围岩的热量传递给喷层，所以喷层内侧温度升高。喷层导热系数从0.5 W/(m·℃)升为3 W/(m·℃)，升高了6倍；喷层内侧温度从6.1℃升为7.1℃，升高了16.39%；喷层外侧温度从60.5 ℃降低到25.9 ℃，降低了57.19%。可以看出，喷层外侧的温度变化远远大于内侧，主要是喷层内侧直接过水的结果。

图6 不同喷层导热系数时喷层外侧温度变化

2.2.2.2应力

在上述温度分布下，喷层的应力变化见图7。从图7可知，喷层导热系数从0.5 W/(m·℃)升到3.0 W/(m·℃)，增大6倍，喷层拱顶的环向应力从7.06 MPa减小到5.31 MPa，减小了22.78%；喷层拱肩的环向应力从4.58 MPa减小到2.47 MPa，减小了46.1%；喷层侧墙中部的环向应力从2.75 MPa减小到0.38 MPa，减小了86.18%。喷层拱顶环向应力随着喷层导热系数的增大呈现减小的趋势，开始呈线性减小，幅度较大，后来慢慢趋于平缓，呈现出抛物线的形式，先增大后减小；喷层拱肩和侧墙中部和拱顶相似。

图7 不同导热系数时喷层应力变化

2.3 比热

2.3.1 围岩比热敏感性

2.3.1.1温度

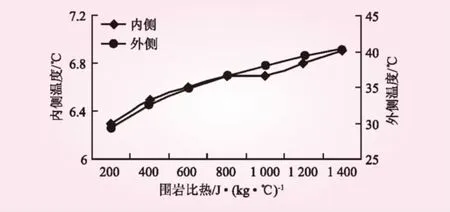
图8 不同围岩比热喷层温度变化

围岩比热不同时喷层内外侧温度变化见图8。从图8可知，随着围岩比热的增加，喷层的内侧和外侧的温度都呈现上升的趋势，这是由于围岩比热越大，围岩在降低1 ℃时释放的热量也就越多，围岩温度降低的幅度就降小，传递给喷层的温度也就会越高。具体来讲，围岩比热从200 J/(kg·℃)升为1 400 J/(kg·℃)，围岩比热升高了7倍，喷层内侧温度从6.3 ℃升为6.9 ℃，升高了9.52%；喷层外侧温度从29.3 ℃升高到40.4 ℃，升高了37.88%。

2.3.1.2应力在上述温度分布情况下，喷层的应力变化见图9。从图9可知，围岩比热从200 J/(kg·℃)升为1 400 J/(kg·℃)，围岩比热升高了7倍，喷层拱顶的环向应力从5.9 MPa增大到6.48 MPa，增大了9.83%；喷层拱肩的环向应力从2.73 MPa增大到3.31 MPa，增大了21.24%；喷层侧墙中部的环向应力从-0.01 MPa增大到1.40 MPa，从压应力转化为拉应力。喷层拱顶环向应力随着围岩比热的增大呈现增加的趋势，但增加趋势开始呈线性增加，幅度较大，后来慢慢趋于平缓，呈现出抛物线的形式，先增大后减小；喷层拱肩规律和拱顶相似；喷层侧墙中部环向应力随着围岩比热的增大呈现增加的趋势，由于喷层应力出现了从压应力到拉应力的转变，其敏感度起始点始于突变点，但总的来说，其敏感度逐渐降低。

图9 不同围岩比热时喷层应力变化

2.3.2 喷层比热敏感性

2.3.2.1温度

喷层比热不同时喷层内外侧温度变化见表2。从表2可知，随着喷层比热的增加，喷层比热从200 J/(kg·℃)升到1 400 J/(kg·℃)，升高了7倍，喷层内侧温度一直为6.7 ℃；喷层外侧温度从38.0 ℃升高到38.1 ℃，升高了0.26%。喷层的内侧和外侧的温度几乎没有变，这是由于喷层特别薄，比热对其影响不明显。

表3 不同喷层比热时喷层关键部位环向应力 MPa

2.3.2.2应力

在上述温度分布下，喷层的应力变化见表3。从表3可知，喷层比热从200 J/(kg·℃)升到1 400 J/(kg·℃)，升高了7倍，喷层拱顶的环向应力从5.93 MPa减小到5.91 MPa，减小了0.34%；喷层拱肩的环向应力从3.22 MPa减小到3.21 MPa，减小了0.31%；喷层侧中的环向应力从1.22 MPa减小到1.21 MPa，减小了0.82%。

2.4 对流系数

2.4.1 温度

对流系数不同时喷层内外侧温度变化见图10。从图10可知，随着围岩对流系数的增加，喷层的内外侧的温度都呈现降低的趋势。围岩对流系数从50 W/(m2·℃)升到5 000 W/(m2·℃)，升高了100倍，喷层内侧温度从11.6 ℃降为5.1 ℃，降低了56.03%；喷层外侧温度从42.2 ℃降为36.4 ℃，降低了13.74%。这是由于围岩对流系数越大，围岩与水换热能力越强，喷层的温度就会降低。

图10 不同对流系数喷层温度变化

2.4.2 应力

在上述温度分布下，喷层的应力变化见图11。

图11 不同对流系数时喷层应力变化

从图11可知，对流系数的增大对喷层的环向应力影响比较明显。对流系数从50 W/(m2·℃)升为5 000 W/(m2·℃)，升高了100倍，喷层拱顶的环向应力从4.57 MPa增大到6.39 MPa，增大了39.82%；喷层拱肩的环向应力从1.93 MPa增大到3.65 MPa，增大了89.12%；喷层侧墙中部的环向应力从-0.01 MPa增大到1.62 MPa，由压应力变化为拉应力。喷层拱顶环向应力随着对流系数的增大呈现出增大的趋势。对流系数为50～1 000 W/(m2·℃)时对喷层的环向应力影响比较大，1 000 W/(m2·℃)以上影响越来越小了。故其敏感度呈现减小的趋势，且开始减小较快，后来慢慢趋于稳定；喷层拱肩和边墙的环向应力和拱顶的变化规律相似。

表4 各参数的敏感度因子

2.5 各参数的敏感度比较

为了定量计算各参数的敏感度因子，将喷层拱顶环向应力设为计算分析依据，对喷层拱顶环向应力的敏感度因子进行汇总，比较分析各参数的敏感程度。各参数的敏感度因子见表4。由表4可知，围岩和喷层的热力学参数对喷层拱顶环向应力的敏感度排序为：喷层线膨胀系数>喷层导热系数>围岩导热系数>对流系数>围岩的线膨胀系数>围岩的比热>喷层的比热。敏感度为0.06时为不敏感参数，本文认为，敏感度因子小于0.1时参数不敏感。因此，围岩线膨胀系数、围岩比热和喷层比热为不敏感参数。

3 结 语

本文以新疆某水电站引水隧洞高地温段为研究背景，对围岩和喷层结构的热力学参数与喷层环向应力的关系进行了分析，并对影响喷层温度场和应力场的围岩和喷层热学参数进行了敏感性分析，得出以下结论：

(1)随着围岩线膨胀系数的增加，喷层拱顶的拉应力线性增大；拱肩和边墙的拉应力呈线性减小的趋势；各部位的敏感度随着围岩线膨胀系数的增大都呈现线性增加的趋势；随着喷层线膨胀系数的增加，喷层拱顶拉应力线性增大，而拱肩和侧墙中部出现压应力转化为拉应力的状态；喷层拱顶环向应力敏感度随着喷层线膨胀系数的增大呈现减小趋势，且减小趋势越来越缓慢，拱肩和侧墙中部喷层应力从压应力转化为拉应力，其敏感度在变化时出现突变。

(2)随着围岩导热系数的增加，喷层拱顶拉应力呈现增大的趋势，开始呈线性增加，幅度较大，后来慢慢趋于平缓，呈现出抛物线的形式，先增大后减小；喷层拱肩和侧墙中部的规律和拱顶相似。随着喷层导热系数增加，喷层拱顶拉应力呈现减小的趋势，开始呈线性减小，幅度较大，后来慢慢趋于平缓，呈现抛物线的形式，先增大后减小；喷层拱肩和侧墙中部和拱顶相似。

(3)随着围岩比热的增加，喷层拱顶拉应力呈现增大的趋势，开始呈线性增加，幅度较大，后来慢慢趋于平缓，呈现出抛物线的形式，先增大后减小；喷层拱肩规律和拱顶相似；侧墙中部由于出现压应力到拉应力的转变，其敏感度起始点始于突变点，但总的来说，其敏感度逐渐降低。由于喷层特别薄，喷层比热增加对喷层的温度几乎没有影响，喷层比热的变化不影响喷层的环向应力。

(4)随着对流系数的增加，喷层拱顶拉应力呈现增大的趋势。对流系数为50～1 000 W/(m2·℃)时，对喷层的环向应力影响比较大，1 000 W/(m2·℃)以上影响越来越小了，其敏感度呈现出减小的趋势，且开始减小较快，后来慢慢趋于稳定；喷层拱肩和边墙的环向应力和拱顶的相似。

(5)通过敏感度因子的计算，围岩和喷层的热力学参数对喷层拱顶环向应力的敏感度排序为：喷层线膨胀系数>喷层导热系数>围岩的导热系数>对流系数>围岩的线膨胀系数>围岩的比热>喷层的比热。围岩线膨胀系数、围岩比热和喷层比热为不敏感参数。

需要指出的是，本文所得到的结论综合考虑了多种因素对应力和温度的影响。现场监测数据表明，支护结构的应力具有一定的变异特性，本文分析未考虑支护结构应力的变异特性，需要做进一步的研究。

[1] 王辉, 陈卫忠. 嘎隆拉隧道围岩力学参数对变形的敏感性分析[J]. 岩土工程学报, 2012, 34(8)： 1548- 1553．

[2] BEIKI M, BASHARI A, MAJDI A. Genetic programming approach for estimating the deformation modulus of rock mass using sensitivity analysis by neural network[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(1)： 1091- 1103．

[3] 朱维申, 章光. 节理岩体参数对围岩破损区影响的敏感性分析[J]. 地下空间, 1994, 14(1)： 10- 15．

[4] 冯夏庭. 智能岩石力学导论[M]. 北京： 科学出版社, 2000．

[5] SAKURAI S, TAKEUCHI K. Back analysis of measured displacement of tunnel[J]. Rock Mechanics and Rock Engineering, 1983, 16(3)： 173- 180．

[6] 杨林德, 冯紫良, 朱合华, 等. 岩土工程问题的反演理论与工程实践[M]. 北京： 科学出版社, 1996．[7] 朱维申, 何满潮. 复杂条件下围岩稳定性与岩体动态施工力学[M]. 北京： 科学出版社, 1995．

[8] 黄书岭, 冯夏庭, 张传庆. 岩体力学参数的敏感性综合评价分析方法研究[J]. 岩石力学与工程学报, 2008, 27(z1)： 2624- 2630.

[9] 李晓静, 朱维申, 向建, 等. 考虑参数影响的系统分析方法及其应用[J]. 岩土工程学报, 2005, 27(10)： 1207- 1210．

[10] 侯哲生, 李晓, 王思敬, 等. 金川二矿某巷道围岩力学参数对变形的敏感性分析[J]. 岩石力学与工程学报, 2005, 24(3)： 406- 410．

[11] 聂卫平, 徐卫亚, 周先齐. 基于三维弹塑性有限元的洞室稳定性参数敏感性灰关联分析[J]. 岩石力学与工程学报, 2009, 28(z2)： 3885- 3893．

[12] LI Shihui, YANG Jie, HAO Weidong, et al. Intelligent back-analysis of displacements monitored in tunneling[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(2)： 1118- 1127．

[13] 黄书岭, 冯夏庭, 张传庆. 岩体力学参数的敏感性综合评价分析方法研究[J]. 岩石力学与工程学报, 2008, 27(z1)： 2624- 2 630．

[14] 章光, 朱维申. 参数敏感性分析与试验方案优化[J]. 岩土力学, 1993, 14 (1)： 51- 57．

[15] 杨蒙, 谭跃虎, 李二兵, 等. 基于敏感性分析的围岩力学参数反演方法研究[J]. 地下空间与工程学报, 1993, 14 (1)： 51- 57．

SensitivityAnalysisofThermodynamicsParametersofSurroundingRockandSupportingStructureinHighGroundTemperatureDiversionTunnel

JIANG Haibo1, WU Peng2, ZHANG Jun2

(1. School of Hydraulic Engineering, Shihezi University, Shihezi 832000, Xinjiang, China;2. Xinjiang Survey and Design Institute for Water Resources and Hydropower, Urumqi 830000, Xinjiang, China)

Taking the section in high temperature field of the diversion tunnel of a hydropower station in Xinjiang as study object, the relationships between the mechanical parameters (thermal conductivity, specific heat, convection coefficient and linear expansion coefficient) of surrounding rock and shotcrete layer structure and the circumferential stress of shotcrete layer are studied based on on-site stress and temperature monitoring data, and the sensitivity of thermodynamic parameters of surrounding rock and shotcrete layer to shotcrete stress is also studied by using parameter sensitivity analysis method. The results show that the main influence factors on the circumferential stress of tunnel vault are ordered as linear expansion coefficient of shotcrete layer, thermal conductivity of shotcrete layer, thermal conductivity of surrounding rock, convection coefficient, linear expansion coefficient of surrounding rock, specific heat of surrounding rock and specific heat of shotcrete layer, in which, the linear expansion coefficient of shotcrete layer, thermal conductivity of shotcrete layer, thermal conductivity of surrounding rock and convection coefficient are more sensitive and the linear expansion coefficient of surrounding rock, specific heat of surrounding rock and specific heat of shotcrete layer are not sensitive to the circumferential stress of tunnel vault．

diversion tunnel; mechanical parameter of surrounding rock; temperature of surrounding rock; circumferential stress; sensitivity analysis

TV223.1(245)

A

0559- 9342(2017)09- 0031- 08

2017- 05- 30

国家自然科学基金项目(51408377)；石河子大学杰出青年科技人才培育计划(2015ZRKXJQ06)

姜海波(1982—)，男，湖南长沙人，副教授，博士，主要从事地下洞室抗冻及稳定性研究工作．

(责任编辑杨 健)