R/S分析在高挡墙位移监测资料分析中的应用

薛 洋，许 雷，陈慧艳

(1.国家能源局大坝安全监察中心，浙江杭州311122；2.大唐(北京)水务工程技术有限公司，北京100000)

R/S分析在高挡墙位移监测资料分析中的应用

薛 洋1，许 雷1，陈慧艳2

(1.国家能源局大坝安全监察中心，浙江杭州311122；2.大唐(北京)水务工程技术有限公司，北京100000)

为了解某高挡墙在运行过程中的安全状况，对其典型断面位移监测资料进行了R/S分析，计算了其Hurst指数、相关系数与分形维数，计算结果表明：位移时间序列的H值均较大，具备着趋势性与随机性双重特征。其中，水平位移的H值接近于1，趋势性较强，垂直位移的H值较接近于0.5，随机性较强；挡墙位移时间序列的分形维数均大于1，说明挡墙位移发展过程中存在着非线性；挡墙右岸出现的降雨入渗导致了水平位移时间序列的H值降低，分形维数升高，结构的非线性特征变得显著，系统更为复杂。

R/S分析；高挡墙；位移；Hurst指数；分形理论

水工建筑物的安全监测是其运行过程中极为重要的一个环节，位移、变形、应力应变等效应量的观测能够用来判断建筑物内部结构的安全状况，为其有效地运行管理提供指导。由于受温度、水位、时效等众多因素的影响，水工建筑物的工作性态极其复杂，其安全监测资料在时间尺度上呈现出高度的非线性，这给资料的分析与预测带来了较大的难度。目前，针对长期的时间序列资料进行分析并作预测的研究成果已取得不少，逐步回归模型、支持向量机模型、神经网络模型、卡尔曼滤波等方法或其组合模型广泛地应用在该领域上[1-2]，并取得了良好的预测效果，但是这些方法均未能揭示出各效应量时间序列自身复杂的本质特征。分形学理论能够从整体角度定量地描述具有不规则结构的复杂系统，由Hurst提出的重标度极差分析法(R/S分析法)是其中的一个代表，它在描述自然界复杂的非线性系统的本质特征及其内在规律上具有良好的效果，已成功地应用在众多工程实践中。李远耀等[3]对三峡库区某个滑坡地区长期位移时序进行R/S分析，发现增量位移时序具有更有效的分形结构，提出了利用Hurst指数判断滑坡加速变形阶段的概念模型；赖道平等[4]利用Hurst重标度和分形学理论分析了某拱坝的裂缝时间序列，研究表明大坝可以看做一个非线性复杂系统，分形维数可从整体上描述大坝动态系统的变化特征并应用于大坝的病害诊断。鉴于此，本文以某抽水蓄能上水库坝后高挡墙位移监测资料为研究对象，分析该高挡墙施工期与运行期的位移发展状况，并利用R/S分析法对位移时间序列的本质特性与分形特征进行分析，揭示该挡墙的位移在未来一段时间内的发展趋势，为今后该高挡墙的安全运行提供指导。

1 R/S分析方法

R/S分析法首先由Hurst提出，后来又经过Mandelbrot等人的补充与完善[5- 6]，目前已经广泛地应用于判断时间序列的分形特征与长程相关性、区分随机与非随机系统，还可以进行趋势性的持续与强度的确定。

1.1 Hurst指数

针对某一观测的效应量序列{xi}，i=1，2，3，…，取某一时间段τ=tn-t1，则该时间段的效应量序列均值xτ为

(1)

在时刻tj(1≤j≤n)观测的效应量的累积均值离差

(2)

极差R(τ)与标准差S(τ)分别为

(3)

(4)

不同的时间段长度(时间尺度不一样)对应的平均重标度极差(R/S)τ的值不一样，Mandelbrot等经过研究发现[10]，lg(R/S)τ与lgτ之间存在着线性关系，即

(5)

以lgτ为横坐标，lg(R/S)τ为纵坐标做散点图，采用最小二乘法作线性拟合，所得直线的斜率即为H值，Hurst指数为刻画时间序列长程相关性的核心参数，θ为常数，表征系统固有特性。

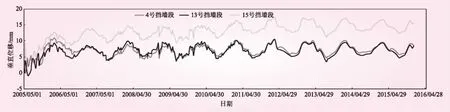
H值的取值范围为0～1，根据其值不同，可以区分时间序列的系统属性，判断其相关性质：①当0≤H<0.5时，表示时间序列是一个有偏的随机过程，具备逆向的持续性状态，过去的时间序列与未来的序列存在着负相关关系，未来的时间序列发展规律将会与过去的相异；②当H=0.5时，表示时间序列是一个标准的随机过程，过去的时间序列与未来的时间序列相互独立，无相关关系；③当0.5

1.2 相关系数C与分形维D

为了量化过去的时间序列对未来的影响程度，Mandelbrot等[7]在1968年引入了一个相关性参数C，

C=2(2H-1)-1

(6)

根据相关的研究资料，时间序列分形维数D和Hurst指数之间存在着如下关系：

D=2-H

(7)

2 某高挡墙位移监测数据分析

某抽水蓄能电站主坝为混凝土面板堆石混合坝，上游由钢筋混凝土面板挡水，下游堆石体建立在陡倾的斜坡上，尾部由最大高度为45.9 m的混凝土重力挡墙拦截坝体。重力挡墙是主坝的安全屏障，因此必须确保重力挡墙安全稳定万无一失。在施工期与运行期，电站均对挡墙的位移、挠度、钢筋应力和锚索应力等效应量进行观测并作分析，挡墙运行状态总体良好，但是2013年来重力挡墙的水平位移有向下游方向缓慢增加趋势，13号墙段向下游水平位移于2014年4月达到运行以来的最大值18.27 mm。为确保重力式挡墙的安全运行，有必要根据位移监测资料对其运行状态进行分析，并揭示其发展规律的内在原因，对未来的发展趋势作相应的预测。本文主要选取了典型挡墙段(右岸13、15号挡墙段，左岸4号挡墙段)的位移监测数据进行分析。

4、13、15号挡墙段的水平位移时间序列见图1，其中水平位移以向下游为正、向上游为负。从图1可以看出，在2007年5月水库蓄水之前，各挡墙段的墙顶水平位移波动较大，处于非稳定状态。上水库蓄水以后，水平位移值逐渐增大，并趋于一个较稳定的水平。但在2012年6月以后，13和15号挡墙段的水平位移出现了增长速率明显加快的趋势，在2014年8月达到了峰值。根据观测人员记录，该地2013年与2014年的降雨量比往常偏大，与此同时，在2014年5月之前，挡墙墙后的堆石体坝坡出现了较多缝隙，为雨水进入坝体并达到建基面提供了良好的渗漏通道，从而引起了坝体堆石体的湿化变形并减小了坝体堆石与建基面间的接触摩擦作用，导致混凝土挡墙墙顶水平位移的增长速率加大。针对该情况，电站管理人员对坝坡裂隙进行了修补，修补后的坝坡基本能够防止雨水的入渗，因此，挡墙墙顶的水平位移有所减小，到目前为止，基本稳定在10 mm左右，仅受季节性温度变化的影响。

图1 不同挡墙段水平位移实测过程线

图2 不同挡墙段垂直位移实测过程线

4、13、15号挡墙段的垂直位移时间序列见图2，其中以垂直位移向上为负，沉降为正。从图2可以看出，在上水库蓄水前，墙顶的垂直位移波动较大，运行期时，挡墙顶部的垂直位移主要受到季节性温度的影响，呈现出较大的周期性波动，仅15号挡墙段有缓慢增长趋势，目前均基本趋于稳定。

3 监测数据的 R/S分析

根据式(1)～(5)，对4、13、15号挡墙段的水平位移与垂直位移时间序列进行Hurst指数计算。这里的水平位移与垂直位移均是累计的绝对位移值。由人工观测的原始数据基本是以一周为等间隔的时间序列，其中部分日期的监测数据有缺失或异常的情况，对异常值进行剔除，对缺失值进行插值补充，最终形成以一周等时距的时间序列。在进行Hurst指数计算时，为了避免较大的统计误差，将τ的初始值取为20，结束值取为100。

不同挡墙段位移时间序列的lg(R/S)τ～lg(τ)相关关系如图3所示，由图3可知，各挡墙段的水平位移与垂直位移时间序列的lg(R/S)τ～lg(τ)图都具备着很好的线性关系，通过最小二乘法进行线性拟合发现各个数据点的拟合度都很高，均超过了0.96。

图3 不同挡墙段位移时间序列lg(R/S)τ～lg(τ)相关关系

由此可以说明，Hurst指数的计算具备较高的可信度，各挡墙段的位移时间序列具有较好的分形特征。

图3中所拟合直线的斜率即为各时间序列的H值，根据式(6)和(7)分别计算出各时间序列的相关关系与分形维数，结果如表1所示。

表1 不同挡墙段位移时序R/S分析结果

从表1可以看出：

(1)不同挡墙段的水平位移时间序列与垂直位移时间序列的H值均大于0.5，由此可以说明，挡墙的位移时间序列随着时间的推移具备趋势性和随机性的双重特性，而且趋势性较为强烈，具备长程相关性[8-9]。即各挡墙段过去的水平位移和垂直位移的发展趋势会延续到未来的一段时间内，可以推测挡墙以后的水平位移还会继续缓慢增长，由季节性温度变化引起的波动性仍然存在；挡墙的垂直位移基本处于稳定状态，增长有限，波动较为明显。

(2)水平位移时间序列的H值较大，均大于0.84，接近1，说明该挡墙水平位移时间序列的趋势性较强，受外界的随机扰动较小，其相关系数较大，接近1，未来水平位移的发展趋势与过去的密切相关。由于挡墙右岸前后坝坡在运行过程中有过破损，降雨入渗导致的湿化引起了13、15号挡墙段水平位移的变化，因此，对13、15号挡墙段在2005年～2014年期间的水平位移时间序列进行了H值计算，结果分别为0.979和0.942，由此可以说明，在挡墙未受到外界突变因素的影响时，其水平位移的趋势性特别强，发展规律较为稳定，分形维数接近1，基本为一个线性系统，当其受到外界因素的影响时，趋势性会减小，分形维数会增加，结构的非线性特征变得显著，系统更为复杂。3处挡墙段的垂直位移时间序列的H值也均大于0.5，但与水平位移相比，其更加接近于0.5，由此可以说明，挡墙的垂直位移趋势性较弱，随机性较强，未来的发展趋势与过去有一定的关系，但仍以明显的波动性为主。

(3)3处挡墙段的位移时间序列的分形维数D比较接近，略大于1，说明该挡墙位移发展过程中仍以线性为主，同时存在一定非线性[10]，故在进行位移资料分析时需将其看作为一个非线性动力系统。

4 结 论

本文主要以某抽水蓄能电站上水库坝后高挡墙的位移监测资料为研究对象，分析了高挡墙的运行状况，并利用R/S分析法对位移时间序列进行了分析，得到以下几点结论：

(1)该高挡墙在运行过程中，水平位移呈现出周期性波动中缓慢上升的趋势，由于右岸墙坝后堆石体出现了降雨入渗导致的堆石湿化，水平位移发生了增长速率加快现象，后期的修补对水平位移的稳定起到了积极作用。垂直位移受季节性温度变化的影响较大，呈现出明显的波动性，总体上升趋势较为缓慢。

(2)不同挡墙段的位移时间序列的lg(R/S)τ～lg(τ)具有良好的线性关系，Hurst指数的计算具有较高的可信度。根据计算结果，位移时间序列的H值均较大，具备着趋势性与随机性双重特征。

(3)挡墙位移时间序列的分形维数较为接近，均大于1，说明挡墙位移发展过程中存在着非线性。由于挡墙右岸墙后坝坡在运行过程中出现过降雨入渗，导致水平位移增长过快，时间序列的H值降低，分形维数升高，结构的非线性特征变得显著，系统更为复杂。

[1] 吴中如, 顾冲时, 沈振中, 等. 大坝安全综合分析和评价的理论、方法及其应用[J]. 水利水电科技进展, 1998, 18(3)： 2- 6．

[2] 苏怀智, 温志萍, 吴中如. 基于SVM理论的大坝安全预警模型研究[J]. 应用基础与工程科学学报, 2009, 17(1)： 40- 48．

[3] 李远耀, 殷坤龙, 程温明. R/S分析在滑坡变形趋势预测中的应用[J]. 岩土工程学报, 2011, 32(8)： 1291- 1296．

[4] 赖道平, 吴中如, 周红. 分形学在大坝安全监测资料分析中的应用[J]. 水利学报, 2004(1)： 100- 104．

[5] HURST H E. Long-term storage capacity of reservoirs[J]. Transactions of the American Society of Civil Engineers, 1951, 116(1): 770- 799．

[6] HURST H E. Long-term storage capacity of reservoirs: an experimental study[M]. American Society of Civil Engineers, 1950．

[7] MANDELBROT B B, Van NESS J W. Fractional Brownian motions, fractional noises and applications[J]. SIAM review, 1968, 10(4): 422- 437．

[8] 范英, 魏一鸣. 基于R/S分析的中国股票市场分形特征研究[J]. 系统工程, 2004, 22(11)： 46- 51．

[9] 庄新田, 庄新路, 田莹. Hurst指数及股市的分形结构[J]. 东北大学学报： 自然科学版, 2003, 24(9)： 862- 865．

[10] 田振华, 孙建会, 朱赵辉. 拱坝结构损伤的多测点R/S分析[J]. 水利水电科技进展, 2014, 34(1)： 65- 67．

ApplicationofR/SMethodinMonitoringDataAnalysisofHighRetainingWall

XUE Yang1, XU Lei1, CHEN Huiyan2

(1. Large Dam Safety Supervision Center of National Energy Administration, Hangzhou 311122, Zhejiang, China;2. Datang (Beijing) Water Engineering Technology Co., Ltd., Beijing 100000, China)

In order to understand the security situation of a high retaining wall in operation, the displacement time series of typical sections are analyzed by R/S method for its nonlinear features including Hurst index, correlation coefficient and fractal dimension calculation. The results show that: (a) the H values of displacement time series are larger and they have double features of tendency and randomness, the H values of horizontal displacement are close to 1 which means strong tendency, and the H values of vertical displacement are close to 0.5 which means strong randomness; (b) the fractal dimension of retaining wall displacement time series are all a little bigger than 1, indicating that the displacement process exists non-linear; and (c) the rainfall infiltration occurred in the right bank causes a reduction of H value and an increase of fractal dimension, which means the nonlinear characteristics of structure being significant and the system being more complex．

R/Smethod; high retaining wall; displacement; Hurst index; fractal theory

lg(R/S)τ=lgθ+Hlgτ

TV698.11

A

0559- 9342(2017)09- 0106- 04

2016- 09- 19

国家自然科学基金重点项目(51139001)；国家自然科学基金项目(51279052)；江苏省“六大人才高峰”项目(JY- 008， JY- 003)

薛洋(1991—)，女，河南三门峡人，助理工程师，硕士，主要从事大坝安全监控方面的工作．

(责任编辑焦雪梅)