类比 探索 感悟—解析几何问题的课堂教学实录及教学反思
周 彬
(浙江省宁波市奉化区第二中学,浙江宁波 315506)
一、基本情况
1.授课对象
授课对象是浙江省一所省二级特色重点学校高二学生,教材使用普通高中新课程标准实验教科书(人民教育出版社),学生数学基础一般,有一定的思考、推理能力,部分学生能大胆地提出假设、问题。学生的自主性和思维的严谨性都有待提高和完善。
2.教学内容分析
本节课教学内容是从学生接触的一个基础题目开始引入的。本题考查直线和圆相切问题中的一个线段的最小值问题,难度不大,但是学生的解答结果不尽如人意。本节课主要通过解决本题,让学生理解一般方法的重要性,然后让学生通过类比的思想方法,将圆推广到我们所学习的椭圆和双曲线。在探索解决这一类问题的本源过程中掌握解决此类问题的一般方法,同时在分组学习讨论中,通过类比的思想方法一起感悟数学知识之间的关联性和统一性,感悟虽然考查的内容不尽相同,但是解决问题的方法和思路又是完全相同的,更进一步感悟数学的美,从而自然生成学生的数学思维。
二、教学过程
1.给出原题引导学生探究

直线AB为圆x2+y2=4的切线,且与x轴、y轴正半轴交于A、B两点,求AB长的最小值。
解:设圆的切线方程为y=kx+m,(k存在)
当x=0时,y=m>0
师:此道题目中,圆的半径固定的情况下,AB长有最小值,同学们思考下,如果半径也发生变化,那AB长的最小值会和什么有关系呢?

生1:AB长的最小值随着半径的变化而变化。
师:非常好,那接下来大家一起探究下。此题改成:
变1.直线AB为圆x2+y2=R2的切线,且与x轴、y轴正半轴交于A、B两点,求AB长的最小值。
留一定的时间给学生思考,教师在教室巡视,然后将其中一位同学的解答展示给同学们。
生2:设圆的切线方程为y=kx+m,(k存在)
当x=0时,y=m>0
师:大家观察下,虽然半径发生改变,但是解题思路和解题过程基本是相同的。大家再考虑下,除了半径发生改变,我们这里还能怎么变化下?
生3:可以将圆变成椭圆,但是不知道AB长是否有最小值?
生4:那圆变成双曲线,AB是否有最小值呢?
师:好,既然不知道能否行得通,那我们一起去尝试下。下面同学们分成2组,合作探究,我们分别解决这两个问题。
学生分组讨论,气氛非常活跃,两组同学分别派出代表作以下解答:
第一组:
生5:解:显然直线斜率是存在的,设直线AB的方程为:y=kx+m,联立方程
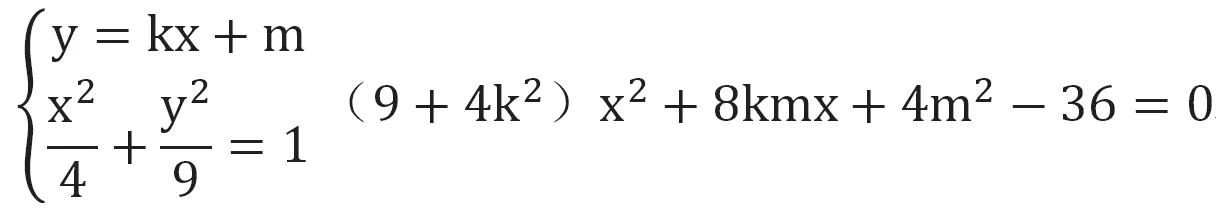
由于Δ=0
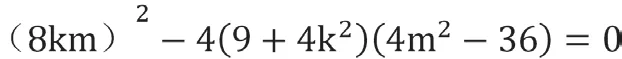
化简得到m2=4k2+9
在直线AB中,令x=0得到y=m

所以AB长度的最小值为5。
师:非常好,请同学们考虑下,与x轴、y轴正半轴交于A、B两点,并且最值情况取到的情况下,k是否能取到?
师:非常好。
第二组:
生6:解:显然直线斜率是存在的,设直线AB的方程为:y=kx+m,联立方程
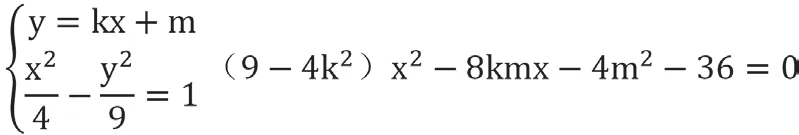
由于Δ=0

在直线AB中,令x=0得到y=m>0
2.及时课堂小结归纳总结
同学们回答得都非常好,我们在求线段AB的最小值时,从特殊的圆变成了圆的一般式,从而得出线段AB的最小值和圆的半径的线性关系。大家又通过类比,将圆变成一个具体的椭圆,这时线段AB依然存在最小值,但是同学们通过分组、合作、探究后计算发现,对于双曲线来说这个最小值又是不存在的。这节课我们更重要的是在探究过程中体会特殊到一般、类比、归纳等思想方法和思维形式。
3.布置课后作业关注课堂延续
那同学们考虑下,如果这里的椭圆是一般形式又能得到什么结论吗?这时AB是否有最小值呢?
解析:显然直线斜率是存在的,设直线AB的方程为:y=kx+m联立方程

由于Δ=0
(2a2km)2-4(a2k2+b2)a2(m2-b2)=0
化简得到m2=a2k2+b2
在直线AB中,令x=0得到y=m>0
三、回顾与反思
1.教学设计的意图
本节课是源自于一次模考考试的原题,虽然这道题非常简单,但是很多同学出现了错误,也有些同学虽然能得出答案,但是忽略掉了斜率的取值范围,从而使解答不够完善。所以课堂更为关注知识的发生过程与学生的数学学习过程的有机统一,由此为依据设置问题情境,引导学生展开观察、猜想、特殊到一般的推广思维活动。同时也发挥了教师的积极主导作用,从特殊到一般,再推广到椭圆中的更为一般的情况,适当调节教学节奏,给不同需求的学生提供不同类别的帮助。
2.教学反思
(1)类比的思想方法。从特殊到一般的推广过程在高中数学中应用非常广泛,但是如何渗透到平时的数学教学中,如何让学生真正了解和掌握这种方法,训练这种思维,是这节课设计的另一个初衷。并且通过圆、椭圆、双曲线的这些变化使学生认识到这些圆锥曲线的有机统一性的特点,更进一步升华。
(2)教学设计从学生的实际出发。数学教学设计不是单一的教师一厢情愿的活动,而是更应该考虑到教学活动中占主体地位的学生,更应该关注到学生的智力、情绪,积极调动学生的学习热情,让他们在探索和合作中寻找对数学奥妙的感知,更进一步促进他们学习数学的热情。
(3)更开阔学生的思维。在本节课中让学生自主去探索、感悟从而理解知识,感受到数学的美。
[1]王洁.中学数学教学中类比思想的培养[J].华中师范大学,2008(09).
[2]叶秀凤.用数学类比思想建构数学有效课堂教学的探析[J].学周刊,2013(28).
[3]周海芳.例谈类比思想在数学教学中的应用[J].宿州教育学院学报,2001(04).

