三角形的并行枚举算法

王 卓，索 勃，潘 巍

(西北工业大学 计算机学院,西安 710129)

三角形的并行枚举算法

王 卓，索 勃，潘 巍*

(西北工业大学 计算机学院,西安 710129)

经典GT算法是三角形并行枚举算法的MapReduce实现，然而该算法只能枚举全图的三角形结构，对部分顶点构成的三角形结构无法直接进行枚举。针对此问题，提出一种直接枚举部分顶点构成三角形结构的并行算法。首先,通过分析被选点的分布，给出被选点构成三角形的所有组合集合；然后，通过对该集合的筛选，实现对部分点构成三角形结构的直接枚举；最后，将该算法在Spark系统实现，以实现该算法的高效性和广泛性。在人工生成数据集和真实数据集上与GT算法进行对比实验，实验结果表明，所提改进算法的运行时间只有GT算法运行时间的1/3，在Spark上的运行时间仅是Hadoop上运行时间的1/7。该算法可用于更高效地直接生成图中任意点所构成的三角形数据集。

三角形枚举；大规模图数据；MapReduce；部分点枚举；Spark

0 引言

在密集图的应用分析中，研究顶点之间的关系是图分析的热点，而对三角形关系的研究又是重要的研究方向。

在图论的研究中，三角形关系是复杂社会网络分析中常见的结构[1]。如在社交网络关系中，通过分析三角性关系可以确定节点之间的联系程度；在角色行为识别中，通过分析三角形关系可以判断角色之间的地位。三角关系的一个重要应用是在枚举图的极大团(Maximal Clique)过程中[2]，即将一跳(one-top，即与被选点直接相邻的点构成的集合)数据转换为三角形结构。

研究者已提出很多算法[3-5]实现一跳数据集向三角形数据集的转换，但伴随着数据量的增大，传统的单机算法已无法快速地处理大规模图数据。随着MapReduce并行计算框架的普及，很多研究已开始使用MapReduce框架进行图数据的处理[6-7]，并且已有研究者实现了MapReduce框架下将一跳数据集向三角形数据集转换的GT(Graph Twiddling)算法[8]。GT算法通过两轮MapReduce 任务来完成数据结构的转换，该算法可以很高效地将整个原图的一跳形式处理成三角形结构，但却无法直接生产部分点的三角形结构。同时，该算法是图上迭代计算，在MapReduce计算框架下，由于需要将中间结果写回磁盘，将造成很大的读写瓶颈。

基于以上两个问题，本文首先提出可直接枚举部分点三角形结构的改进GT算法，该算法经过两轮MapReduce任务：第一轮为查询点的筛选，第二轮为查询点三角形结构的生成；同时，将改进算法在Spark系统上实现，以实现该算法高效迭代的特性。本文的主要工作如下：

1) 改进GT算法，使该算法可以直接生产部分点的三角形结构；同时，在三角形的筛选过程中，提出按照最小度数点进行切分的优化思想，以提高枚举效率。

2) 将改进算法在Spark系统实现，避免因MapReduce框架下需要将中间结果写回磁盘的瓶颈，以提高迭代计算效率。

3) 通过合成数据集和真实数据集验证该算法的高效性，与改进前相比，具有至少3倍的运行效率提升。

1 相关技术

本章介绍与本文研究密切相关的两个概念：三角形结构和MapReduce计算框架。

1.1 三角形结构

设无向图G=(V,E)，其中：V是顶点的集合，|V|是顶点的总数；E是边的集合，|E|是边的总数。

定义1 三角形结构。给定一个无向图G=(V,E)，{u,v,w}∈V，若三个顶点满足以下关系{u,v}，{w,v}，{u,w}∈E，则称三个顶点构成了一个三角形结构，记为△uvw。

1.2 MapReduce计算框架

MapReduce计算模型是将计算分为Map和Reduce两个阶段。在Map阶段，由用户定义的map函数将输入的每条元组转换为〈key,value〉形式，然后按照partition函数对key进行分区，并将各分区Shuffle到Reduce端，且严格保证分区和Reducer是一一对应的关系。当各Reducer获取分配给各自分区的全部数据后开始执行用户定义的reduce函数，并输出结果。

影响Reducer执行效率的关键是partition函数的定义，合理的partition函数可以实现各Reducer运行过程中的均衡性，反之会出现数据倾斜，严重影响执行效率。对于数据的分配均衡问题，文献[9]已进行了探讨并提出了相应的策略。该问题的避免可以通过定义partition函数或定义map函数等方法优化，因此，在设计MapReduce算法时应该考虑该数据倾斜的问题。

MapReduce在处理迭代计算时，有两处磁盘操作，map函数后和reduce函数的结果输出，因此MapReduce在处理图的迭代计算时存在数据传输的瓶颈问题。针对该问题，已有i2MapReduce[10]方法可进行高效的迭代计算，同时Spark系统更是被广泛应用的图处理平台。

2 GT算法

本章介绍基于MapReduce编程模型的GT算法。

GT算法将三角形的枚举过程分为两个MapReduce任务：第一，合并公共点；第二，判断合并后的公共点集合中是否存在三角形结构。

第一轮MapReduce任务：map函数将同一节点的所有邻接点进行汇总，并传到一个Reducer上处理。reduce函数将与该点相连，且编号大于该点的所有顶点进行笛卡尔积运算，并将结果输出。

第二轮MapReduce任务：map函数将原图和第一轮Reduce端的输出结果合并，即边作为key值输出。reduce函数判断第一轮笛卡尔积所构成的边集合中，是否存在原图中的边。若在原图中存在该边，则说明该边的两个顶点与生成该边的点，即第一轮中reduce函数key所表示的顶点，构成了一个三角形结构。

根据对GT算法的描述可知，在第一轮Reduce阶段，需要进行笛卡尔积操作，度数较大的点会产生大量的中间结果。GT算法在处理时，将原图以一跳的形式表示，并满足第一个顶点编号的值小于第二个顶点编号的值，同时，将度数小的顶点作为key值，然后再进行分区，从而达到减少中间结果的目的。

GT算法不能直接枚举出部分点所构成的三角形结构。由于第一轮map函数是按照度数或者顶点编号进行划分的，因此在枚举部分点构成的三角形结构时，当被选点出现在value中，就无法获得被选点的完整邻接点集合，从而导致查询的结果不完整。因此，若使用GT算法来枚举部分点的三角形结构，首先需要枚举出原图的所有三角形，然后从全图的三角形集合中筛选出包含被选点的结构。由此可见，这样将造成大量的不相关计算。

3 PGT算法

本章介绍可直接枚举部分顶点构成三角形结构的改进GT算法，本文称为PGT(Parts-of-vertex for GT)算法。

3.1 算法描述

要解决GT算法直接枚举部分点构成三角形结构的问题，就需要解决如何在划分过程中保持数据的完整性问题，因此首先需要统计出被选点划分后的分布情况。由于MapReduce模型采用〈key,value〉对处理数据的特点，在数据划分后被选点只会现在两个集合中：第一是在key中，如图 1(a)所示的第一层顶点编号为A的顶点(被选点)；第二个是在value中，如图 1(b)所示的第二层顶点编号为B的顶点(被选点)。因此，要保证数据的完整性需要同时将两种情况进行分析。

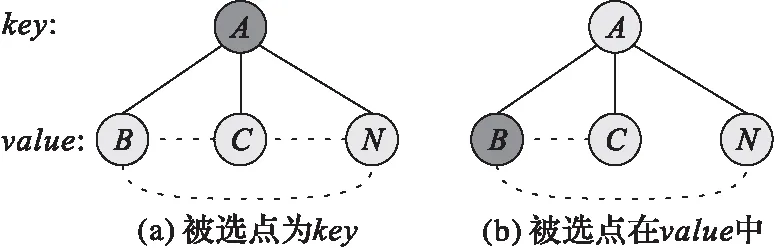
图 1 被选点的分布Fig. 1 Distribution of candidate vertexes

如图 1(a)所示，被选点在key集合中。在该结构中，value集合中的顶点是key的邻接点集合，如图中实线所示。在该结构中若存在三角形，一定是value中的某两个顶点存在一条边，即如图中虚线所示。因此，对于这种情况，需要将value集合中的所有顶点进行笛卡尔积运算，即构建出一条新边，并通过下一轮MapReduce任务判断该边是否在原图中存在，若存在，则该点(key)与相连的两点(value中的顶点)构成了三角形结构。

如图 1(b)所示，被选点出现在value中。出现这种情况的原因是：为了减少笛卡尔积集合的大小，在划分时是以两个点的度数为标准，即度数小的点为key，因此导致被选点会出现在value中的现象。在此种结构中，同样value集合中的点是key点的邻接点，然而只需要枚举包含有被选点的集合。因此，此时只需要将被选点从value中取出，然后将该点和value中的其他点进行笛卡尔积运算，构建出一条新边，如图 1(b)中虚线所示。同样，通过下一轮MapReduce任务判断该边是否在原图中存在，若存在，则该点(value中的被选点)和相连的两个点(key顶点和在value中与被选点相连的顶点)构成了三角形结构。

3.2 算法实现

算法1 PGT算法的MapReduce实现。

输入 集合key,集合value,被选点构成的集合Cand;

输出 候选边集Edge。

1)

ifkeyinCand

//被选点在key集合中

2)

forvtovalue

//遍历value集合，求笛卡尔积

3)

Edge←v×{value-v}

4)

Write(Edge,key)

//输出，并标注是在key集合中

5)

endfor

6)

endif

7)

else

8)

forntovalue

//被选点在value集合中

9)

ifninCand

10)

Edge←n×{value-n}

11)

Write(Edge,n)

//输出，并标注是在value集合中

12)

endif

13)

endfor

14)

endelse

算法1可分为两部分：第一部分从1)～6)行，是对被选点在key中情况的处理，第二部分从7)～14)行，是对被选点在value中的处理。由于在第二轮MapReduce任务中，需要将被选点进行聚合，所以在输出时，需要标明被选点的编号，即如算法1第4)行和第11)行所示。由算法1描述可知，该算法的复杂度为O(n)。

算法2 PGT算法的Spark实现。

输入 集合key，集合value，被选点构成的集合Cand;

输出 三角形边集edges。

1)

defPGT(key: Int,value:Set[Int],Cand:Set[Int])={

2)

if (Cand.contains(key)) {

3)

for (v←value){

//遍历value集合

4)

valnotV=value-v

5)

valedges=notV.map(v2 => {

6)

(v,v2)

// 对value中的点求笛卡尔积

7)

})

8)

(edges,key)

//第一种情况的输出

9)

}

//end for

10)

}

//end if

11)

else {

12)

for (n←value) {

13)

if (Cand.contains(n)){

//被选点在value中

14)

valnotN=value-n

//除去本点后求笛卡尔积

15)

valedges=notN.map(n2=> {

16)

(n,n2)

//第二种情况的输出

17)

}

18)

(edges,n)

19)

}

//end if

20)

}

//end for

21)

}

//end else

22)

}

//end function

算法2由两部分组成：第一部分从1)～10)行，是对被选点在key中情况的处理，第二部分从11)～22)行，是对被选点在value中的处理。函数PGT()是Spark中reduce函数的参数，即实现对三角形的筛选工作，不同于MapReduce的输出，Spark的输出可存储在内存中，以实现迭代计算的高效性。

4 实验结果及分析

本章通过两部分实验验证GPT算法的高效性，实验是在两个人工生成数据集和两个真实数据集上进行，通过随机选点的方法比较两个算法的运行时间。

4.1 实验环境

本文的所有实验在11个节点的集群上进行，其中包含1个Master节点负责任务的调度和集群管理， 10个Worker节点负责存储数据和计算。每个节点的系统配置为:16 核主频为 2.20 GHz 的AMD 处理器，16 GB 的 RAM 和 1 TB的硬盘，节点之间通过1 Gb的网络连接，各节点用的是 64 位Ubuntu Linux12.01，部署的是Hadoop-1.2.1版本和Spark-1.6.1。

配置Hadoop，设置每个节点有10个Map slots和6个Reduce slots，采用默认的Hash分区函数，其他配置设置为默认值。为增强实验的说服力，同一组实验运行5次，取5次结果的平均值作为最终结果。

4.2 实验数据

对于两种数据源作去重和格式化处理，并将数据处理为1-跳的形式。实验数据分为合成数据和真实数据，合成数据通过GTgraph[11]生成，包含DARPA HPCS SSCA (SSCA)和Recursive Matrix (R-MAT)数据，SSCA的参数设置：顶点数为220，极大团的大小为100；R-MAT设置顶点数为104，边与顶点的比值为1 000。真实数据包含两种SOCIAL NETWORKS[12]数据，数据的分布情况如表1所示。

表 1 实验数据Tab. 1 Experimental data

4.3 对比实验

本节在合成数据集和真实数据集上比较两种算法的运行时间。实验采用随机选点，验证选点个数的不同对两种算法运行时间的影响。由于GT算法首先需要将一跳数据集全部转换为三角形数据集，这部分需要两轮MapReduce任务完成，经过5次测试，这部分的平均时间为3 200 s。由于是处理部分点，在对比实验部分，不将这部分的时间计算在内；因此运行时间的统计分别为：GT算法为从全部三角形数据集中读取部分点的时间，PGT算法为从一跳数据集直接生产部分点的三角形数据集的时间。

图2(a)、(b)分别是两种算法在合成数据集SSCA和R-MAT上的实验，图2(c)、(d)分别是两种算法在真实数据集Orkut和Twitter上的实验。通过结果可以发现，GT算法和PGT算法都有很好的稳定性，而从运行时间上来看，在SSCA和R-MAT数据集上，GT算法的运行时间是PGT算法的3倍和4倍。随着输入数据量的增大，在真实数据集Orkut和Twitter上，GT算法的运行时间都是PGT算法运行时间的11倍。由此可见PGT算法在运行效率上有很大的提升。

4.4 Spark性能实验

由于GT算法本身只有MapReduce实现，因此本节给出PGT算法在Hadoop和Spark系统上运行的对比实验，使用的数据集为图2(d)的Twitter数据集，对比实验如图3所示。

从图3结果可以看出，Spark系统在运行时间上比Hadoop系统有近7倍的性能提升，这主要因为Spark在迭代过程中未将结果写入磁盘，从而减少了对磁盘的读写操作。

图2 GT和PGT算法在不同数据集上的运行时间对比Fig. 2 Runtime contrast of GT and PGT on different datasets

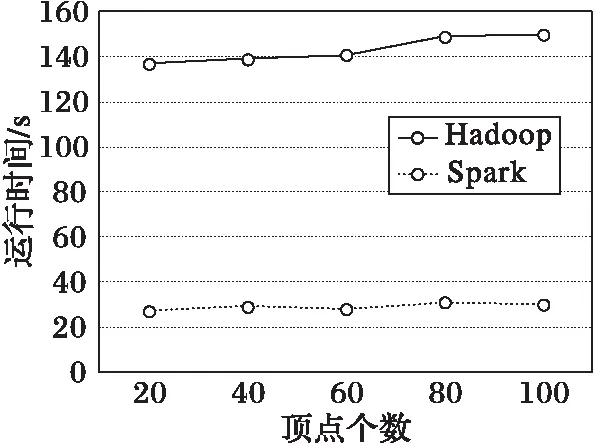
图3 Spark与Hadoop上PGT算法运行时间对比Fig. 3 Runtime contrast of PGT algorithm on Spark and Hadoop

5 结语

本文提出一种改进的PGT算法，用于枚举部分点的三角形结构，并给出算法的MapReduce实现和Spark实现方法。该算法与传统算法相比，可以在三角形的生成过程中，只生成部分点的三角形结构，而避免对非筛选节点的三角形枚举工作，并最后在合成数据集和真实数据集上，验证该算法的高效性。三角形枚举是图数据研究中重要的应用，今后可通过本文的方法实现快速的三角形结构枚举。

References)

[1] PARANJAPE A, BENSON A R, LESKOVEC J. Motifs in temporal networks [C]// Proceedings of the 2017 Tenth ACM International Conference on Web Search and Data Mining. New York: ACM, 2017: 601-610.

[2] WANG Z, CHEN Q, HOU B Y, et al. Parallelizing maximal clique andk-plex enumeration over graph data [J]. Journal of Parallel and Distributed Computing, 2017, 106: 79-91.

[3] COHEN J. Trusses: cohesive subgraphs for social network analysis [R]. Fort Meade, MD: National Security Agency, 2008.

[4] 金宏桥,董一鸿.大数据下图三角计算的研究进展[J].电信科学,2016,32(6):153-162.(JIN H Q, DONG Y H. Research progress of triangle counting in big data [J]. Telecommunications Science, 2016, 32(6): 153-162.)

[5] SHAIK F, SUBRAMANYAM R, SOMAYAJULU D. Map-reduce based multiple sub-graph enumeration using dominating-set graph partition [J]. International Journal of Information Engineering and Electronic Business, 2017, 9(2): 36-44.

[6] QIN L, YU J X, CHANG L J, et al. Scalable big graph processing in MapReduce [C]// Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2014: 827-838.

[7] SALIHOGLU S, WIDOM J. GPS: a graph processing system [C]// Proceedings of the 25th International Conference on Scientific and Statistical Database Management. New York: ACM, 2013: Article No. 22.

[8] COHEN J. Graph twiddling in a MapReduce world [J]. Computing in Science & Engineering, 2009, 11(4): 29-41.

[9] 王卓,陈群,李战怀,等.基于增量式分区策略的MapReduce数据均衡方法[J].计算机学报,2016,39(1):19-35.(WANG Z, CHEN Q, LI Z H, et al. An incremental partitioning strategy for data balance on MapReduce [J]. Chinese Journal of Computers, 2016, 39(1): 19-35.)

[10] ZHANG Y F, CHEN S M, WANG Q, et al. i2MapReduce: incremental MapReduce for mining evolving big data [J]. IEEE Transactions on Knowledge and Data Engineering, 2015, 27(7): 1906-1919.

[11] BADER D A, MADDURI K. GTGraph: a synthetic graph generator suite [EB/OL]. [2017- 05- 06]. https://www.researchgate.net/publication/228993783_GTGraph_A_synthetic_graph_generator_suite.

[12] ROSSI R A, AHMED N K. The network data repository with interactive graph analytics and visualization [C]// Proceedings of the 2015 Twenty-Ninth AAAI Conference on Artificial Intelligence. Menlo Park: AAAI, 2015: 4292-4293.

This work is partially supported by the Ministry of Science and Technology of China, National Key Research and Development Program (2016YFB1000703), the National High Technology Research and Development Program of China (863 Program) (2015AA015307), the Key Program of National Natural Science Foundation of China (61332006), the General Program of National Natural Science Foundation of China (61672432, 61472321), the National Natural Science Foundation of China for Young Scholars (61502390).

WANGZhuo, born in 1984, Ph. D. candidate. His research interests include graph data management, distributed computing platform.

SUOBo, born in 1987, Ph. D. candidate. His research interests include graph data management.

PANWei, born in 1978, Ph. D., associate professor. His research interests include memory computing.

Parallelalgorithmfortriangleenumeration

WANG Zhuo, SUO Bo, PAN Wei*

(SchoolofComputerScience,NorthwesternPolytechnicalUniversity,Xi’anShaanxi710129,China)

The classical Graph Twiddling (GT) algorithm is the MapReduce implementation of triangle parallel enumeration algorithm. However, the GT algorithm can only enumerate the triangle structure of whole graph and can not enumerate the triangle structure of candidate vertexes directly. To solve the problem, a parallel algorithm was proposed for directly enumerating the triangle structure of candidate vertexes. Firstly, the set of all the combinations of candidate vertexes for forming triangle was given by analyzing the distribution of candidate vertexes. Then, through the screening of the set, the triangle structure of candidate vertexes was directly enumerated. Finally, the proposed algorithm was implemented on Spark to achieve high efficiency and popularity. The contrast experiment was completed on artificial datasets and real datasets. The experimental results show that, compared with the GT algorithm, the running time of the proposed algorithm is only 1/3 of the running time of GT algorithm, and the running time on Spark is only 1/7 of the running time on Hadoop. The proposed algorithm can be used to generate the triangle dataset of any candidate vertex directly and efficiently.

triangle enumeration; large-scale graph data; MapReduce; candidate vertex enumeration; Spark

2017- 07- 04;

2017- 09- 05。

中国科技部国家重点研发计划项目(2016YFB1000703)；国家863重大项目(2015AA015307)；国家自然科学基金重点项目(61332006)；国家自然科学基金面上项目(61672432，61472321)；国家自然科学基金青年项目(61502390)。

王卓 (1984—)，男，河南濮阳人，博士研究生，CCF会员，主要研究方向：图数据管理、分布式计算平台； 索勃(1987—)，男(满族)，辽宁锦州人，博士研究生，主要研究方向：图数据管理； 潘巍(1978—)，男，陕西西安人，副教授，博士，CCF会员，主要研究方向：内存计算。

1001- 9081(2017)12- 3397- 04

10.11772/j.issn.1001- 9081.2017.12.3397

(*通信作者电子邮箱wzhuo918@mail.nwpu.edu.cn)

TP311.131

A