基于非正交多址的认知MIMO网络次用户系统容量优化
廖 晗,马东亚,尹礼欣
(移动通信技术重庆市重点实验室(重庆邮电大学),重庆400065)
基于非正交多址的认知MIMO网络次用户系统容量优化
廖 晗*,马东亚,尹礼欣
(移动通信技术重庆市重点实验室(重庆邮电大学),重庆400065)
针对未来移动通信系统对大容量、高频谱利用率的需求,提出基于非正交多址 (NOMA) 技术的认知多输入多输出(MIMO)网络次用户系统容量优化方法。首先对发送信号进行预编码,随后按照信道质量增益对认知用户进行分簇,再对分簇之后的用户进行功率分配,最后将得到的NP-hard型多簇目标函数转化为求各子簇的容量;同时兼顾认知用户服务质量(QoS)及满足串行干扰消除(SIC)的条件,利用Lagrange函数结合Karush-Kuhn-Tucker(KKT)条件求解出分簇之后的最优功率分配系数,且该系数是0到1之间的常数。仿真结果表明,所提方法优于平均功率分配方法,并且在信道质量较差时,相比基于正交多址(OMA)技术的认知MIMO,显著提高了次用户系统容量。
非正交多址; 认知多输入多输出网络;分簇;功率分配;Lagrange函数;Karush-Kuhn-Tucker条件
0 引言
认知无线电技术与多输入多输出(Multiple-Input Multiple-Output, MIMO)技术结合的网络称之为认知MIMO网络,其借助MIMO的空域并行传输优势,能够较大幅度提升系统的容量。面对即将到来的5G时代,频谱稀缺依然是一个严峻的问题,而认知MIMO兼具认知无线电的智能灵活性和MIMO的空间传输优势,能够在提升频谱利用率的同时提高系统的容量,对于未来移动通信具有广泛的前景[1]。1G到4G均采用正交多址接入技术,5G时代,非正交多址接入技术日益受到产业界的关注,不仅能进一步增强频谱效率,也是逼近多用户信道容量界的有效手段[2]。相对于认知MIMO的其他模式,underlay频谱共享以其较高的频谱效率和可实现性成为了一种更具吸引力的共享模式[3],在该模式中,主用户和次用户同时工作,它们占用相同的频段完成自身通信,但认知用户(次用户)对授权用户的有害干扰不能影响授权用户的正常通信;否则,认知用户不能工作[4]。
非正交多址技术(Non-Orthogonal Multiple Access, NOMA)是一种在发送端主动引入干扰,在接收端采用串行干扰消除手段进行信号接收的新型多址接入技术[5],自这项技术被提出至今,越来越多的研究者将NOMA与MIMO结合起来研究,还有一小部分研究者将NOMA与认知无线电联合起来进行研究,主要目的都是提升系统的频谱利用率及提高系统容量,但目前该类研究相对较少。文献[6]中,采用求解一元二次方程的最大值方式求得最优解,这种算法简单且所得解是全局最优解,但此种方式仅能求解只有两个次用户的情景,不具有普适性;文献[7]仅研究了众多次用户中符合要求的两个用户,且该文献未对发送信号进行预编码设计,这样不能很好地进行干扰控制;文献[8]研究了下行链路的NOMA多用户波束成形系统,其将多个用户分成若干簇,每簇中仅有两个用户,并要求基站拥有的发射天线数与簇的数目相同,这对基站天线数不满足要求的情况不适合。本文根据文献[8]重新设计次用户簇的数目,根据次用户基站的有效天线数目来决定分簇的数目,即:若次用户基站有两根有效发射天线,则将次用户分成两个簇。由文献[9]可知,功率因素对信道质量差的用户的影响远大于信道质量好的用户,因此,在进行功率分配时,给信道状态差的用户分配较多的功率,信道状态好的用户分配较少的功率,这种功率分配相比于传统的注水功率分配方式更有利于系统性能提升。
1 系统模型
考虑一个多用户的下行链路通信网络,认知系统采用underlay频谱共享模式,此时,需要考虑次用户系统对主用户系统的干扰约束,次用户接收来自次用户基站的信号,信号包括有用信号和干扰信号,主用户接收来自次用户基站的干扰信号,系统模型如图1所示。假设次用户发射天线为Nt根,次用户数目为N个,为便于分析,设次用户分成Nt个簇,且每个簇中有K个次用户,若每个簇中K是不变的,则有NtK=N,且设每根天线的功率占总功率的比例相同。
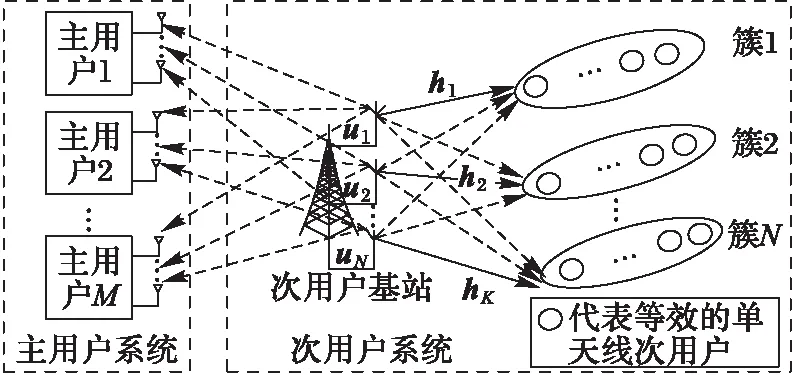
图1 系统模型Fig. 1 System model
次用户基站发送的信号表示为:
x=[x1,x2,…,xNt]∈CNt×K
矩阵x代表基站的发送信息序列,则有:
那么,有:
式中:xn是发送至第n个簇的信号;xn,k是发送至第n个簇中的第k个用户的信号;an,k代表发送至第n个簇中的第k个用户的功率分配系数;Pt代表次用户基站实际发送功率;sn,k代表发送至第n个簇中的第k个用户的数据信息。
根据系统模型可知,次用户基站发送信息给Nt个簇中的N个次用户,同时,在发送端进行预编码,预编码矩阵为U=[u1H,u2H,…,uNtH]∈CNt×Nt(H代表矩阵或者向量的共轭转置),主用户系统也会收到来自次用户基站的干扰。本文根据文献[10]的式(1),得到系统模型第n个簇中的第k个次用户接收到的信息为:
yn,k=χ(hn,kUx+zn,k)=
(1)
NOMA系统中接收端采用串行干扰消除方式进行接收,也就是接收端进行解码之前先消除其他用户的干扰信号,且信道质量好的用户在获得所需信号时,不受其他用户的干扰,根据文献[6]的式(5) ~ (6),则接收端的信息式(1)可写为:

(2)
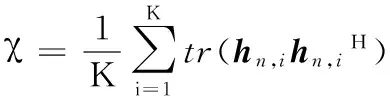
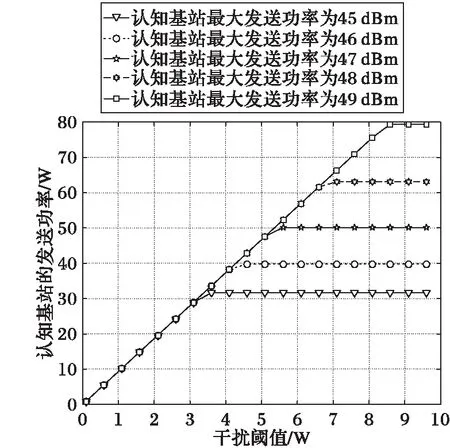
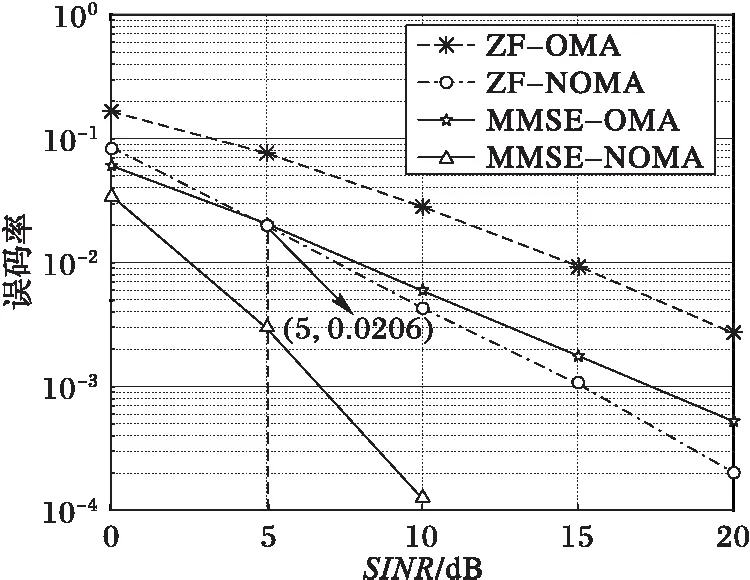
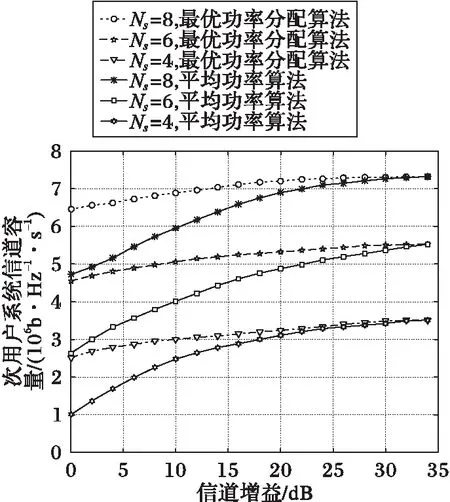
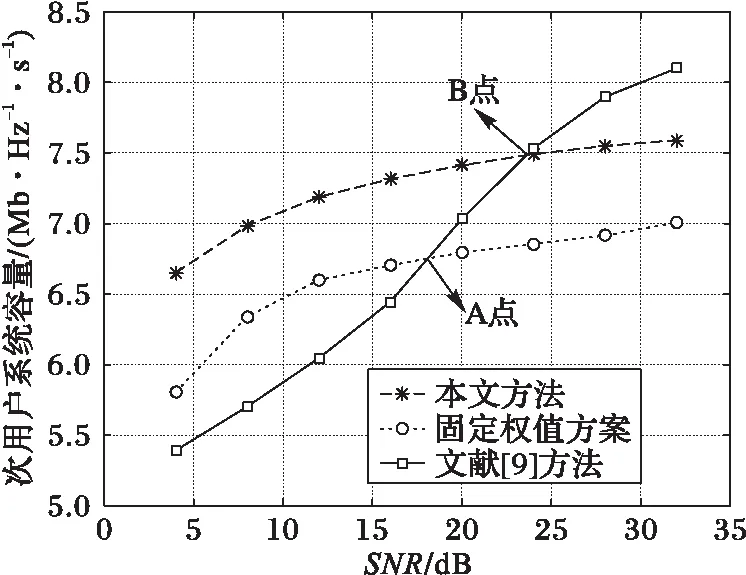
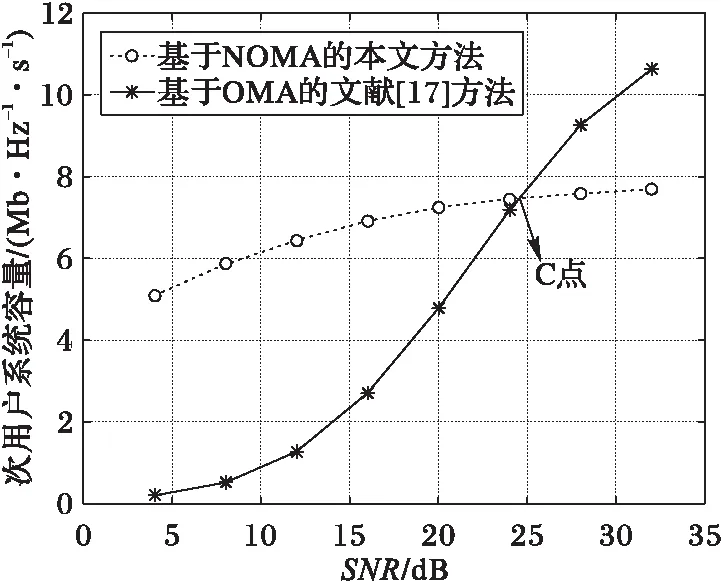
由文献[9]可知,功率因素对信道质量较差的用户影响远大于信道质量好的用户,因此考虑功率因素对信道质量的影响要达到进一步提高系统的整体性能的目的,给信道质量好的用户分配较少功率,信道质量差的用户分配较多功率。假设第n个簇中,信道增益为|hn,1|2>|hn,2|2>…>|hn,K|2,则相应的功率分配系数为an,1 (3) 假设E[|si,j|2]=1,∀i,j,则第k个用户的容量为: (4) 式中,B代表每个发送波束的带宽,且有: (5) 其中:gn,k代表归一化信道增益,对信道进行归一化能够起到简化计算的目的。那么,式(3)可以写为: (6) 整个次用户系统的容量为: (7) 本文假设主用户配有128根天线,次用户基站配有2根天线,共有Ns个次用户并且每个次用户均配有1根天线,将整个次用户分成两个大簇,每个簇中有K个次用户,则Ns=2K。 underlay模式下的基于NOMA的认知MIMO系统主要考虑次用户基站对主用户系统的干扰以及次用户系统分簇之后的簇间干扰和簇内干扰,其他干扰不是主要干扰,为了研究的简便,本文不予考虑。工作于underlay模式下,次用户系统对主用户系统的干扰必须小于预定的阈值Ip,当满足此条件时,主用户和认知用户均可正常工作;当干扰大于阈值时,认知用户不能正常工作[11],即次用户的存在是以不影响主用户正常通信为前提,此时认知基站实际最大发射功率为Pt。Pt的计算式如下: (8) 由于是认知MIMO系统,则认知基站的发射功率要兼顾主用户系统和认知基站自身的性能,图2为干扰阈值与认知基站的发射功率之间的关系图。由图2可以得到主用户的干扰阈值与认知基站的发射功率之间的关系曲线,当次用户对主用户的干扰功率门限增大时,认知基站的发射功率也随之呈线性增大趋势,但是由于认知基站自身的发射功率具有一定的极限值,所以,当干扰阈值达到一定值时,认知基站的实际发射功率维持在其所能容忍的最大发射功率上,这样,保证认知基站工作于正常状态同时,维持认知系统正常工作。 图2 干扰阈值与认知基站发送功率的关系Fig. 2 Relationship between interference threshold and transmitting power of cognitive base station 图3 不同预编码方式的误码率比较Fig. 3 Comparison of BER for different precoding methods 图3比较了四种不同的预编码方式,其中基于正交多址的迫零(Zero-Forcing, ZF)预编码误码率要远远高于其他三种预编码方式,而采用非正交多址的MMSE误码率要远远低于其他三种预编码方式,且在SINR=10 dB时,误码率为零。当SINR<5 dB时,四种不同的预编码方式的误码率从大到小分别为:ZF-OMA> ZF-NOMA > MMSE-OMA >MMSE-NOMA;当SINR≥5 dB时,四种不同的预编码方式的误码率从大到小分别为:ZF-OMA>MMSE-OMA>ZF-NOMA>MMSE-NOMA。 由文献[7]可知,分簇需要使分在同一簇的用户之间的信道相关性和差异性都尽可能大,这样对于干扰抑制和有用信号接收都有利。Kim等[14]将次用户系统分为两个簇,将信道增益强的分为一簇,信道增益弱的分成另一簇,这样分簇能够保证信道之间的相关性,但是信道之间的差异性却不能得到保证。文献[15]是单天线的NOMA系统,其采用头尾分簇方式。本文根据文献[14]的分簇方式,先将次用户按照归一化信道增益从大到小的顺序进行排序,即:g1>g2>…>gNs-1>gNs,然后再进行分簇。这里,本文考虑每个簇中次用户的数量为奇数和偶数两种情况,将整个次用户系统分成两个簇,即n={1,2}。 经过分簇及预编码之后,可以得到该簇的容量为式(9),本文的目标就是求式(9)的最大值。 (9) 由文献[14]可知,次用户系统每簇进行串行干扰消除时,各用户之间的功率需要满足: 令ptol×(Pt/2)-1=β,R0/B=γ,这里β、γ为常数。R0是次用户需要满足的最低速率,当次用户的速率大于等于R0时,才能正常工作;否则,不能正常工作。经过以上分析,根据系统模型可以得出系数分配的优化方程: C4:an,k∈[0,1]; n={ 1,2} ,∀k=1,2,…,K 式中:约束C1表示进行功率分配之后系数之和小于等于1;约束C2对次用户的速率进行限制,次用户系统中的每个用户的速率都满足大于一定值,从而保证次用户的用户服务质量;约束C3表示已经解码的次用户与尚未解码的次用户之间最小的功率之差大于ptol;约束C4表示功率分配系数要满足的条件。 对约束C2进行简化分析,有: 再由Lagrange函数可得: 根据KKT(Karush-Kuhn-Tucker)条件可得: (10) (11) (12) (13) 对由系统模型得出的系数分配的优化方程进行分析可知,原问题是一个非凸的NP-hard(Non-deterministic Polynomial-hard)问题[16],想要求解最优值是很难的,本文采用Lagrange函数及KKT条件结合数学归纳法对以上问题进行求解,并对求解的值进行验证是否符合要求。 设O={λ};Ω={η1,η2,…,ηK};Θ={ζ1,ζ2,…,ζK},由于K≥2,所以可得Lagrange函数L(an,k,λ,η,ζ)最优解的集为:Ψ={λ,η2或ζ2,η3或ζ3,η4或ζ4,…,ηK或ζK},本文假设满足认知系统的最小速率的条件,即:Ψ={λ,ζ2,…,ζK},且ζ1=η1=η2=…=ηK=0时,此时有: (14) (15) ∀k=1,2,3,4 (16) 由式(14)~(15)可解得当每组次用户数目为2、3、4时的功率分配系数。 当K=2时,每簇中每个次用户的功率分配系数为: 当K=3时,每簇中每个次用户的功率分配系数为: 当K=4时,每簇中每个次用户的功率分配系数为: 由数学归纳法得到每簇簇头的功率分配系数为: 由簇中的其他K-1个用户,可得功率分配系数为: 2≤k≤K,n={1,2} 最后根据KKT条件的性质进行验证。验证当N=8的情况,此时,每个簇中有四个次用户,即:K=4,此时,假设Ψ={λ,ζ2,ζ3,ζ4},Θ={ζ2,ζ3,ζ4}。令式(10)等于0,再根据几何运算,可以得到如下关系式: 根据等式性质,可以解得: ζ1=ηk=0;k=1,2,3,4 另外,当次用户系统采用平均功率分配方式时,an,k=1/K,此时系统容量为: 为了进一步提升认知MIMO网络次用户系统的容量,提出了基于非正交多址接收的动态功率分配优化算法。该算法主要思想是:根据认知基站的有效发射天线数,确定分簇的数目,对整体次用户进行分簇之后,为保证次用户之间的公平性,根据信道质量的优劣对次用户进行功率分配,给信道质量好的次用户分配较少功率,给信道质量差的次用户分配较多功率,这样的功率分配即可保证次用户之间的相对公平性。在对系统模型进行分析之后,写出目标函数,再根据约束条件列出约束方程,这样就得到系统的优化方程,对优化方程进行分析可知,其是非凸的NP-hard型问题,直接求解是很困难的,并且无法用凸优化理论进行求解。本文的求解过程为:首先写出优化方程的Lagrange函数,再根据KKT条件进行最优功率分配系数的求解,最后根据数学归纳法得出使得目标函数最优的功率分配系数。并且由于是基于NOMA的认知MIMO网络,那么接收端采用串行干扰消除进行有用信号的接收,这样能够有效降低系统的误码率,从而进一步提高认知系统的容量。 本章验证基于NOMA的认知MIMO认知系统的容量问题。仿真参数设置:为了使本文更符合未来移动通信的实际场景,将主用户收发天线设置为128根,这样可满足将本文所提方法适用于未来大规模MIMO场景中,认知基站有2根收发天线,认知用户数目大于等于4且用户均配置单根收发天线。本文在设置的仿真参数的过程中,尽可能地贴合实际应用场景。其他仿真参数如表1所示。 实验一 采用蒙特卡罗仿真比较了次用户数目不同的情况下,动态功率分配和平均功率分配两种方式下,次用户系统的容量变化。由图4可以看出,采用动态功率分配方式,随着次用户数目的增多,系统容量也会逐渐增多,且次用户从4个增多到6个时,系统容量的提高要比次用户从6个增加到8个提高得更多。同等条件之下,在信道质量相对较差时,采用本文进行的最优功率分配系数方法,能够保证次用户之间的公平性,充分发挥功率分配的优势,达到提高次用户系统容量的目的,而采用平均功率分配方式,将认知基站的实际发射功率平均分配给次用户系统的所有用户,其功率分配与信道质量没有关联,也没有兼顾次用户之间的公平性,所得系统容量低于最优功率分配方法,因而所得的系统容量小于采用最优功率分配方法所得系统容量;当信道质量达到较好状态时,此时信道质量对次用户系统容量的影响就相对减少,动态功率分配方式与平均功率分配方式所得系统容量趋于稳定的最大值。由此可知,本文的动态功率分配方式要比平均功率分配方式获得的系统容量多,其要优于平均功率分配方案,仿真结果如图4所示。 表1 仿真参数Tab. 1 Simulation parameters 图4 不同数量的次用户系统容量随信道增益变化曲线Fig. 4 Changing curve of different number of secondary user system’s capacity with channel gain 由图5可知,由于主用户的存在,认知基站的发送功率受限,所以当发送功率达到一定值时,系统容量呈逐渐增大的趋势,但是当认知基站的发射功率达到一定高度时,认知系统的容量最终趋向于稳定状态。由图5中的交点A可知,本文以信道矩阵迹的均值作为加权系数的最优功率分配方法只有在全部信道均很差的情况之下,才会获得较差的加权系数,因而优于固定权值方案;再由图5中的交点B可知,在信道质量相对较差时,本文所求得的最优动态功率分配系数方法要优于文献[9]采用的方法。 图5 基于NOMA的不同方法次用户系统容量对比Fig. 5 Comparison of secondary user system’s capacity for different methods based on NOMA 实验三 在与实验二相同的仿真参数下,将本文方法与文献[17]基于速率分配的传统的基于正交多址技术的认知MIMO进行对比。由文献[17]可知,采用速率分配方式在提升认知系统容量方面具有显著的优势,且该文献是一篇关于认知无线电速率分配的具有代表性的文献,因而实验三将本文提出的优化方法与文献[17]方法进行比较。与实验二相同,主用户的存在会影响次用户基站的发射功率,当次用户基站的发送功率达到一定程度时,次用户系统容量增加幅度逐渐降低,最终趋于恒定状态。采用速率分配方式受限于设置的最大最小反馈速率及认知基站的发送功率两个限制条件,将基于非正交多址(NOMA)的本文方法与基于正交多址(Orthogonal Multiple Access, OMA)的文献[17]方法进行仿真对比,可以得到仿真结果如图6所示。 由图6中的交点C可知,在认知用户数Ns=8时,相比于文献[17]的最优功率算法,在信道质量相对较差的情况下,本文方法所得的系统容量要远高于基于正交接入的速率分配方案。 图6 不同方法的认知MIMO对比Fig. 6 Comparison of cognitive MIMO for different methods 串行干扰消除是以增加接收机的复杂度为代价提高系统容量的,随着集成电路进一步的发展,对于未来移动通信,NOMA技术是增加系统容量的一项重要候选技术。本文针对认知MIMO与NOMA技术的结合对次用户系统容量的提升的问题进行研究,在对模型进分析之后,列出系数分配优化方程,再结合Lagrange函数及KKT条件等数学推导求解出每簇每用户的最优功率分配系数,然后代入求解系统容量,最后利用Matlab软件进行系统容量的仿真验证。仿真验证表明:在信道状态相对较差时,所提方法能够较大幅度地提高系统的容量。下一步将考虑新的预编码方式和功率分配方式,进一步优化道状态好的情况下NOMA认知MIMO的次用户系统容量。 References) [1] 朱世磊,周游,任修坤,等.认知MIMO干扰网络的顽健干扰对齐算法[J].通信学报,2016,37(3):157-164.(ZHU S L, ZHOU Y, REN X K, et al. Robust interference alignment algorithm for cognitive MIMO interference network [J]. Journal on Communications, 2016, 37(3): 157-164.) [2] 毕奇,梁林,杨姗,等.面向5G的非正交多址接入技术[J].电信科学,2015,31(5):14-21.(BI Q, LIANG L, YANG S, et al. Non-orthogonal multiple access technology for 5G systems [J]. Telecommunications Science, 2015, 31(5): 14-21.) [3] 荣玫,朱世华,李锋.认知无线电网络基于F范数的频谱共享[J].电子学报,2011,39(1):95-100.(RONG M, ZHU S H, LI F. Spectrum sharing based on Frobenius norm in cognitive radio networks [J]. Acta Electronica Sinica, 2011, 39(1): 95-100.) [4] SLIMENI F, SCHEERS B, NIR V L, et al. Learning multi-channel power allocation against smart jammer in cognitive radio networks [C]// Proceedings of the 2016 International Conference on Military Communications and Information systems. Piscataway, NJ: IEEE, 2016: 1-7. [5] 李世超.5G关键技术之NOMA介绍[J].电子制作,2015(4):139-140.(LI S C. The NOMA introduction of 5G key technology [J]. Practical Electronics, 2015(4): 139-140.) [6] ZABETIAN N, BAGHANI M, MOHAMMADI A. Rate optimization in NOMA cognitive radio networks [C]// Proceedings of the 2016 8th International Symposium on Telecommunications. Piscataway,NJ: IEEE, 2016: 62-65. [7] DING Z G, FAN P Z, POOR H V. Impact of user pairing on 5G nonorthogonal multiple-access downlink transmissions [J]. IEEE Transactions on Vehicular Technology, 2016, 65(8): 6010-6023. [8] KIM B, LIM S, KIM H, et al. Non-orthogonal multiple access in a downlink multiuser beamforming system [C]// Proceedings of the 2013 IEEE Military Communications Conference. Piscataway, NJ : IEEE, 2013: 1278-1283. [9] 周志栋,谢显中,邵奇.多小区环境中基于动态功率分配的干扰安排算法[J].吉林大学学报(信息科学版),2011,29(6):504-510.(ZHOU Z D, XIE X Z, SHAO Q. Research on interference alignment based on dynamic power allocation in multi-cell [J]. Journal of Jilin University (Information Science Edition), 2011, 29(6): 504-510.) [10] CHEN Z Y, DING Z G, XU P, et al. Optimal precoding for a QoS optimization problem in two-user MISO-NOMA downlink [J]. IEEE Communications Letters, 2016, 20(6): 1263-1266. [11] ZENG M, TSIROPOULOS G I, DOBRE O A, et al. Power allocation for cognitive radio networks employing non-orthogonal multiple access [C]// Proceedings of the 2016 IEEE Global Communications Conference. Piscataway, NJ: IEEE, 2016: 1-5. [12] LIU Z X, LEI L, ZHANG N B, et al. Joint beamforming and power optimization with iterative user clustering for MISO-NOMA systems [J]. IEEE Access, 2017, PP(99): 1-11. [13] LYU T K. Capacity of Multi-user MIMO systems with MMSE and ZF precoding [C]// Proceedings of the 2016 IEEE Conference on Computer Communications Workshops. Piscataway, NJ: IEEE, 2016: 1083-1084. [14] KIM B, CHUNG W, LIM S, et al. Uplink NOMA with multi-antenna [C]// Proceedings of the 2015 IEEE 81st Vehicular Technology Conference. Piscataway, NJ: IEEE, 2015: 1-5. [15] ALI M S, TABASSUM H, HOSSAIN E. Dynamic user clustering and power allocation for uplink and downlink Non-Orthogonal Multiple Access (NOMA) systems [J]. IEEE Access, 2016, 4: 6325-6343. [16] BOYD S, VANDENBERGHE L. Convex Optimization [M]. Cambridge, UK: Cambridge University Press, 2004: 243-244. [17] 谢显中,何露,杨和林,等.认知无线电中具有双重代价因子的联合功率控制与速率分配博弈算法[J].中国科学:信息科学,2015,45(9):1157-1168.(XIE X Z, HE L, YANG H L, et al. Joint power control and rate allocation game algorithm with dual pricing factors in cognitive radio networks [J]. SCIENTIA SINICA Informationis, 2015, 45(9): 1157-1168.) This work is partially supported by the Program for Changjiang Scholars and Innovative Research Team in University (IRT1299), the Project of Special Fund for Chongqing Science and Technology Commission Key Laboratory (cstc2013yykfA40010). LIAOHan, born in 1991, M. S. candidate. Her research interests include cognitive radio, non-orthogonal multiple access, energy harvesting. MADongya, born in 1992, M. S. candidate. His research interests include cognitive radio, interference alignment. YINLixin, born in 1993, M. S. candidate. His research interests include mobile communication, massive multiple-input multiple-output. CapacityoptimizationofsecondaryusersysteminMIMOcognitivenetworksbasedonnon-orthogonalmultipleaccess LIAO Han*,MA Dongya, YIN Lixin (ChongqingKeyLabofMobileCommunicationsTechnology(ChongqingUniversityofPostsandTelecommunications),Chongqing400065,China) Concerning the demands of large capacity and high spectrum utilization in future mobile communication system, a method for optimizing the capacity of secondary user system in Multiple-Input Multiple-Output (MIMO) cognitive networks based on Non-Orthogonal Multiple Access (NOMA) was proposed. Firstly, the transmitted signals were pre-coded, and then the cognitive users were clustered according to channel gains. Secondly, the power allocation was performed for users after clustering. Finally, the Non-deterministic Polynomial-hard (NP-hard) multi-cluster objective function was transformed into solving the capacity of each sub-cluster. Meanwhile, taking into account Quality of Service (QoS) of cognitive users and requirement of Successive Interference Cancellation (SIC), the optimal power allocation coefficient, which is a constant between 0 and 1, was solved by using Lagrange function and Karush-Kuhn-Tucker (KKT) condition. The simulation results show that, the proposed method outperforms the average power allocation method. And when the channel quality is poor, compared with the MIMO cognitive network based on Orthogonal Multiple Access (OMA), the proposed method has improved the capacity of secondary user system significantly. Non-Orthogonal Multiple Access (NOMA); Multiple-Input Multiple-Output (MIMO) cognitive network; clustering; power allocation; Lagrange function; Karush-Kuhn-Tucker (KKT) condition 2017- 06- 26; 2017- 09- 05。 长江学者和创新团队发展计划项目(IRT1299);重庆市科委重点实验室专项经费资助项目(cstc2013yykfA40010)。 廖晗(1991—),女,湖北襄阳人,硕士研究生,主要研究方向:认知无线电、非正交多址、能量收集; 马东亚(1992—),男,安徽阜阳人,硕士研究生,主要研究方向:认知无线电、干扰对齐; 尹礼欣(1993—),男,安徽铜陵人,硕士研究生,主要研究方向:移动通信、大规模多输入多输出。 1001- 9081(2017)12- 3361- 07 10.11772/j.issn.1001- 9081.2017.12.3361 (*通信作者电子邮箱13594678449@163.com) TN929.5 A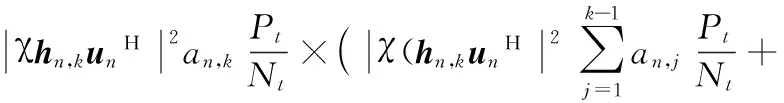
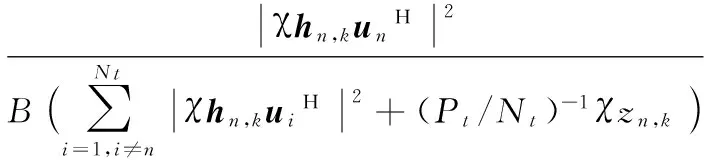
2 问题描述及解决方案
2.1 认知系统
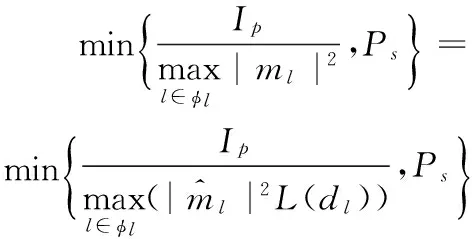

2.2 预编码方式

2.3 分簇方式
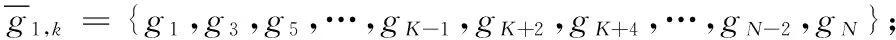

2.4 功率分配及问题求解
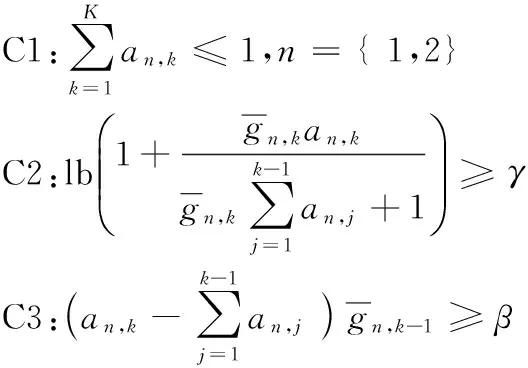
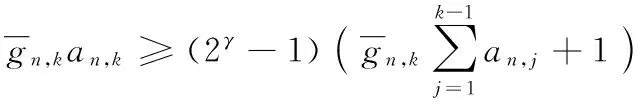
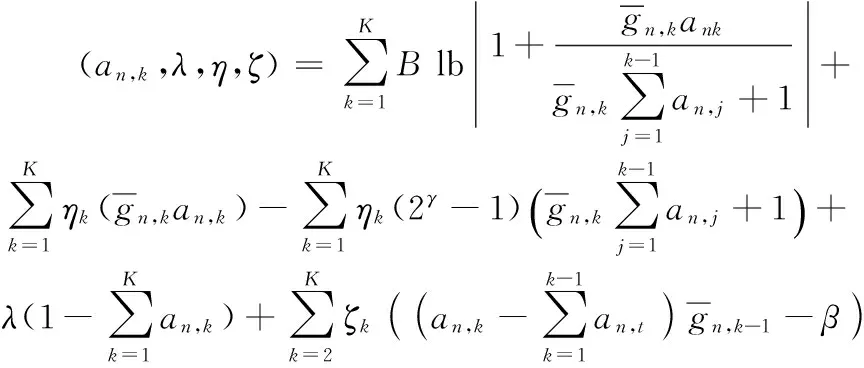
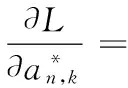
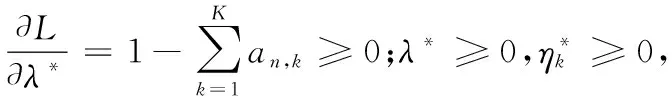


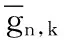
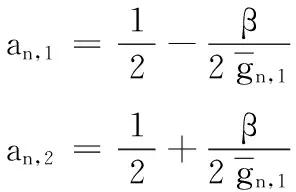
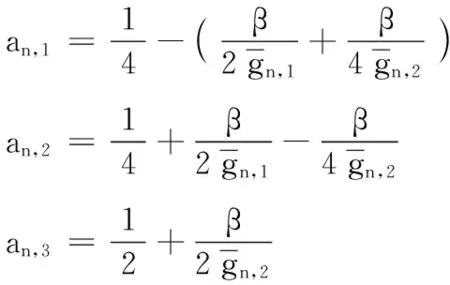
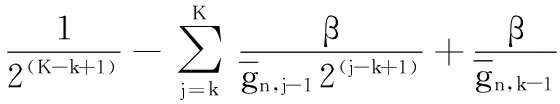
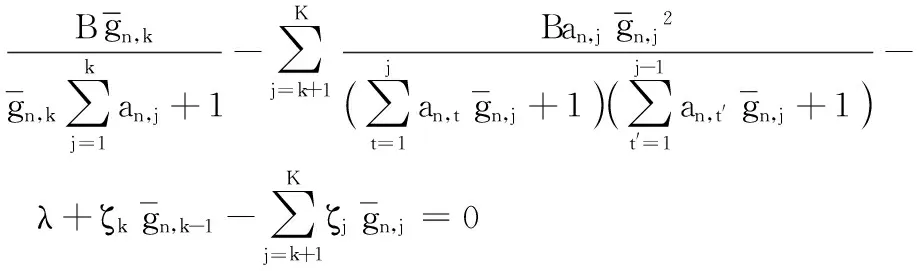
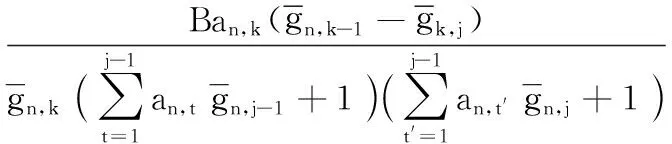

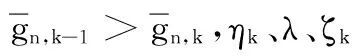

2.5 算法描述与分析
2.6 算法的复杂度分析

3 仿真结果与分析

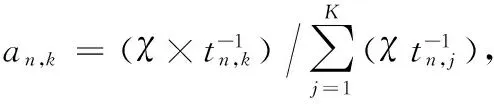
4 结语

