空间太阳能电池金属栅线极限尺寸的理论研究
刘嘉歆,冯仕猛,雷 刚,顾梦奇,龚小童,钟晓霞
(1.上海交通大学 物理与天文系,上海 200240; 2.上海空间电源研究所,上海 200245)
空间太阳能电池金属栅线极限尺寸的理论研究
刘嘉歆1,冯仕猛1,雷 刚2,顾梦奇2,龚小童1,钟晓霞1
(1.上海交通大学 物理与天文系,上海 200240; 2.上海空间电源研究所,上海 200245)
对空间太阳能电池金属栅线空间尺寸对电子平均自由程和电导率的影响进行了理论研究。考虑金属栅线空间尺寸小于100 nm和大于电子自由程两种情况,建立了栅线空间尺寸对其平均自由程影响的物理模型,推导出栅线中电子平均自由程和电导率计算公式。计算机模拟表明:当栅线空间尺寸较小(小于2倍自由程)时,其对应的电子自由程和电导率随栅线空间尺寸的增加而快速增大,反之则快速减小;当栅线空间尺寸大于100 nm时,栅线的边界对电子自由程和电导率有影响,其对应的自由程和电导率随栅线高度和宽度增加而增大,空间尺寸不同影响程度亦不同;当栅线高度和宽度达到800 nm时,电子自由程和电导率达到最大值。理论上,太阳能电池栅线高度和宽度可做到800 nm,可作为将来太阳能电池栅线制备的一个方向。
空间太阳能电池; 金属栅线; 空间尺寸; 栅线边界; 平均自由程; 电导率; 物理模型; 自由电子
0 引言
金属栅线是太阳能电池的一个重要部分,副栅线引导电流,主栅线收集副栅线电流,起汇总作用。太阳能电池栅线电极包括设置在电池片上的主栅线,数量4~10根,宽度0.1~2.5 mm;副栅线数量100~200根,宽度10~39 μm。栅线有一定的面积,它会减少进入电池的光子数量,从而降低转换电池的转换效率。但目前太阳能电池栅线的研究主要集中于优化设计和工艺技术,重点研究银浆配方、线栅的制备工艺等[1-7]。但减小低栅线空间尺寸、增加电池表面的受光面积、提高太阳能电池的转换效率等,需要相应的理论作支撑。减小低栅线空间尺寸,一般会增加其对应的电阻,但详细的影响机理有待研究。以前研究栅线的电导率时,常将属栅线作为块状材料,不考虑金属栅线不同于块状材料的表面散射、接触散射、电子隧道等特性。文献[8-9]在F-S理论基础上,考虑表面和晶界的散射,提出了电导率与厚度的关系式,主要针对薄膜电导率的尺寸效应。另外,金属电导率与材料中电子自由程有关,研究电子自由程与空间尺寸的关系,可给出电导率与空间尺寸的理论表达。早期的Fuchs-Sondheimer理论模型只考虑了边界散射;Mayadas-Shatzkes 模型虽然考虑了晶界散射,但它同样是针对超薄膜结构,并有很多假设[10]。目前,关于栅线中自由程、电导率与空间尺寸的关系的文献很少。
寻找更好的设计方案和技术线路,降低栅线面积,增加电池片的受光面积,尽量使更多的光子进入太阳能电池中,是未来太阳能电池线栅研究的一个方向。本文根据电子自由程的定义,给出栅线空间尺寸对电子自由程影响的物理模型,研究了空间尺寸对电子自由程和电导率的影响,给出空间太阳能电池栅线可能的极限尺寸,可为太阳能电池线栅的研究提供参考。
1 金属栅线中电子自由程理论模型
1.1 金属栅线空间尺寸小于100 nm
金属材料中电子自由程一般40~50 nm。当金属栅线高度和宽度小于100 nm时,对应的电导率会受二维空间尺寸的影响。金属电导率取决于电子平均自由程,金属中电子平均自由程越长,材料电导率越大;反之,电子平均自由程越短,材料电导率越小。
为便于研究,以电子自由程为半径画出自由程球,自由程球在线栅中与线栅重叠的部分分为1、2、3区。其中:1、2区完全相同;3区是自由程球与线栅重叠部分并扣除4个球冠后的空间。设线栅的高度和宽度相同,均为d,不影响理论研究结果。
栅线尺寸效应如图1所示。图1中:栅线的高度和厚度均为d;OA与金属块状材料中电子平均自由程λ相等。以OA为半径作一个自由程球,则由点O出发的自由电子运动到栅线表面会发生碰撞,碰撞回到栅线中再与其他电子相撞,从而影响电子的自由程。
上述模型中自由程球的体积为

(1)
对图1中完全相同的1、2区,即栅线空间和自由程球的重叠区的体积相当于一个球冠,约等于图2所示的体积,则对应的体积
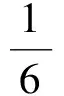
(2)
比较图1、2,可发现式(2)中对应参数的表达式为
(3)
将(3)代入式(2),则得球冠的体积为
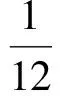
(4)
图1中自由程球与线栅重叠部分并扣除4个球冠后的体积(相当于图1中的第3区)
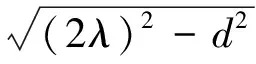
则,栅线中能提供给电子自由运动体积为
(5)
由于线栅边界限制,电子实际自由运动空间变小,则会导致电子自由程减少。根据电子自由程的定义,本文提出栅线中电子自由程应修正为
(6)
由金属电导率与自由程的关系可得金属栅线电导率
(7)
因块状金属电导率σ0=kλ(此处:k为比例常数),则式(7)可变为
(8)
对应的电阻率公式修正为
(9)
式中:ρ为金属栅线电阻率。
1.2 金属栅线空间尺寸大于电子自由程时
当金属栅线的空间尺寸远大于电子自由程时,图2中仅有栅线表面层,或图3中粗实线围成的1、2区的电子才能与边界发生相撞,从而影响对应的自由程。为使1、2 区域中的电子不与边界发生相撞,须多出无任何电子的空间,如图3中点线与栅线表面围成的3、4区,这相当于多给出的虚拟空间。若栅线存在这部分虚拟空间,则栅线中1、2 区的电子不会发生与边界发生相撞。
由此模型,则电子与边界不发生相撞所需的体积
V=(d+λ)2l
(10)
式中:l为栅线的长度。电子真正能活动空间的体积
V2=d2l
(11)
因边界有碰撞,故电子自由程表达式修正为
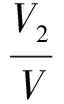
(12)
将式(12)代入电导率公式中,其栅线的电导率

(13)
式中:σ0为块状金属的电导率。
2 讨论
2.1 不同空间尺寸的栅线平均自由程与电阻率
由图1推导出的式(6)、(9),若栅线高度和宽度超过2倍的自由程,则式(6)、(9)中的根号内为负数,两式无意义。因此,式(6)、(9)的使用条件是栅线高度和宽度必须小于2倍的自由程。对栅线高度和宽度小于2倍的自由程时,用式(6),计算机模拟所得不同自由程的栅线高度和宽度(均相同)如图4所示,其中金、银和铜块体材料对应的电子自由程分别为40,30,20 nm。由图4可知:栅线高度和宽度小于2倍的自由程时,栅线中电子平均自由程将随其高度和宽度增加而增大;反之,则变小。当高和宽度都超过2倍的自由程时,若不考虑边界对电子自由程的影响,则栅线电子平均自由程将达到块体材料的自由程,其自由程为一常量(如图4中三条曲线的直线部分)。
由式(9)和金、银、铜的σ0(分别为0.020 65,0.015 9,0.016 7 Ω·mm2/m),计算机模拟可得不同空间尺寸的栅线电阻率如图5所示。由图5可知:随着金栅线高度和宽度的增加,电阻率不断降低,电导率不断增大。当d超过40 nm时,电阻率是一条趋向于零的直线。
2.2 栅线边界对平均自由程影响
当栅线空间尺寸远大于块体材料平均电子自由程时,用式(12),计算机模拟出不同栅线厚度的自由程和电导率如图6所示。其中:图6(a)是式(12)中的d在100~10 000 nm间的关系曲线;图6(b)是式(12)中的d在100~1 000 nm的关系曲线。由图6(b)可知:当栅线的高度和宽度为100~300 nm时,高度和宽度对电子自由程有影响,栅线中电子平均自由程随其对应的高度和宽度增加而增大;当栅线的高度和宽度为300~800 nm时,高度和宽度对电子自由程影响程度逐渐减小,栅线中电子平均自由程将随其对应的高度和宽度增加而缓慢增大;当栅线高度和宽度大于800 nm时,自由程将达到块体材料的自由程,如图6(a)所示。
栅线边界对其电导率影响的关系如图7所示。其中:图7(a)是式(13)中的d为100~10 000 nm的结果;图7(b)是式(13)中的d为100~1 000 nm的结果。由图7(b)可知:栅线空间尺寸的大小对其电导率有影响,其影响程度随空间尺寸不同而各异,当栅线的高度和宽度为100~300 nm时,栅线电导率随其对应的高度和宽度增加而增大;当栅线的高度和宽度为400~800 nm时,栅线电导率随其对应的高度和宽度增加而缓慢增大,如图7(b)所示;当栅线高度和宽度大于800 nm时,电导率将达到块体材料的电导率,如图7(a)所示。
综上所述,理论上太阳能电池栅线高度和宽度可为800 nm。考虑栅线中存在孔洞、杂质等对自由程的影响,其极限宽度最小可为1 000 nm左右,使电池表面收集到更多的光子,以提高其转换效率。
3 结论
本文给出了栅线尺寸影响栅线中电子平均自由程的物理模型,推导了不同条件下栅线中自由电子平均自由程的计算公式。研究表明:当空间尺寸小于2倍的自由程时,栅线中电子平均自由程随空间尺寸的增加而快速增大,反之,则快速减小;当栅线高度和宽度尺寸大于100 nm时,栅线中边界对电子平均自由程和对应的电导率有影响,空间尺寸不同,影响程度不同;当栅线高度和宽度为800 nm时,电导率达到极限值。研究所得的此结论对空间太阳能电池线栅的研究有一定的参考意义。
[1] 杨乐, 高华. 太阳电池栅线优化设计[J]. 光电技术应用, 2012, 27(1): 41-44.
[2] 施小忠, 汪乐, 夏冠群. 太阳电池栅线的设计[J]. 电子学报, 1999, 27(11): 126-127.
[3] 牛源, 卞宝安, 杨健, 等. 网版参数对单晶硅太阳电池栅线印刷的影响[J]. 半导体技术, 2012(12): 37-41.
[4] 许鸿雁, 张景洋, 李景, 等. 丝网印刷网版对太阳电池片细栅线高度及电池性能的影响研究[J]. 太阳能, 2014(3): 34-36.
[5] 刘翔. 太阳能电池栅线电极的优化设计[J]. 新能源, 1998(5): 9-13.
[6] ZOU J, YIP H L, HAU S K, et al. Metal grid/conducting polymer hybrid transparent electrode for inverted polymer solar cells[J]. Applied Physics Letters, 2010, 96(20): 203301.
[7] LIU W, LI Y, CHEN J, et al. Optimization of grid design for solar cells[J]. Journal of Semiconductors, 2010, 31(1): 42-45.
[8] 范平, 伍瑞锋, 赖国燕. 连续金属栅线的电阻率研究[J]. 真空科学与技术, 1999, 19(6): 445-451.
[9] 范平. 超薄金属膜的电导特性[J]. 金属学报, 1999, 19(6): 445-451.
[10] MAYADAS A F, SHATZKES M. Electrical-resistivity model for polycrystalline films: the case of arbitrary reflection at external surfaces[J]. Physical Review B, 1970(1): 1382-1389.
TheoreticalResearchofLimitSizeofMetallicGridinSpaceSolarCell
LIU Jia-xin1, FENG Shi-meng1, LEI Gang2, GU Meng-qi1, GONG Xiao-tong1, ZHONG Xiao-xia1
(1. Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China;2. Shanghai Institute of Space Power-Source, Shanghai 200245, China)
The influence of space size of metal grid line on the electron mean free path and conductivity were studied theoretically in this paper. The physical models to describe the effect of metal grid line’s space size on the mean free path and conductivity were established with the conditions considered in which the first was the gird line size smaller than 100 nm and the second was the gird line size lager than electronic free path. The formula for calculating the electron mean free path and conductivity in the grid line was derived. Computer simulations show that both the mean free path and the electronic conductivity rapidly increase with the increase of space size of the grid line when the grid size is very small (smaller than 2 times of electronic free path). Inverse, the mean free path and the electronic conductivity will rapidly decrease. The different size has different influence. When the size of the gate line space is more than 100 nm, the boundary of the gate line also has an influence on the electronic free path and conductivity. The corresponding free path and conductivity increase with the increase of the height and width of the gate. When the height and width of the gate line reach 800 nm, the electronic free path and conductivity reach the maximum value. In theory, the height and width of the solar cell can be 800 nm, which is a direction for the preparation of the solar cells.
space solar cell; metal grid line; spactial dimension; grid line boundary; mean free path; electronic conductivity; physical model; free electron
2016-11-14;
2017-05-21
国家自然科学基金资助(11275127);航天先进技术联合研究中心资助(USVAST2015-28)
刘嘉欣(1995—),女,硕士生,主要研究方向为材料表面物理。
1006-1630(2017)06-0115-05
TM914.4
A
10.19328/j.cnki.1006-1630.2017.06.018

