迈克耳孙-莫雷实验对狭义相对论的建立起到重要作用了吗？

王欣懿 陈婉盈 张元仲

(1北京陈经纶中学，北京 100020; 2中国科学院理论物理研究所，北京 100190)

迈克耳孙-莫雷实验对狭义相对论的建立起到重要作用了吗？

王欣懿1陈婉盈1张元仲2

(1北京陈经纶中学，北京 100020;2中国科学院理论物理研究所，北京 100190)

本文对迈克耳孙-莫雷实验提供了3种解释：静止以太说的解释、静止以太说+洛伦兹收缩的解释，以及双程光速各向同性的解释。然后分析了寻找光以太的实验(包括迈克耳孙-莫雷实验)对爱因斯坦建立狭义相对论所起的作用。

迈克耳孙-莫雷实验；静止以太说；洛伦兹收缩；双程光速各向同性

在牛顿时代，解释光的传播现象存在两种假说：一种是微粒说，另一种是波动说。19世纪初，光的干涉和衍射现象被发现之后，光的波动说被普遍接受。人们把光波与声波进行类比，由于声波不是独立的物质存在而是媒介的振动，所以没有媒介也就没有声音(真空中不会有声音)。由此，物理学家开始设想宇宙中充满一种看不见摸不着的光媒介(称之为“以太”)，靠这种以太，光波才得以产生并传播。为了寻找以太的物理效应，物理学家设计过各种不同类型的实验装置用以检验以太的存在。迈克耳孙-莫雷实验只是其中的一种：1881年，迈克耳孙首先使用干涉仪的转动检验以太风的速度，但是他没有观察到以太漂移的效应。1887年，迈克耳孙和莫雷以更高的精度重新做了实验，同样没有观察到条纹移动。迈克耳孙-莫雷实验的零结果在很多狭义相对论的书籍和文章中被说成是对狭义相对论的建立起到了重要作用。我们对实验零结果提供了3种解释并阐述迈克耳孙-莫雷实验对爱因斯坦建立狭义相对论所起的作用。

1 静止以太说对迈克耳孙-莫雷实验零结果的解释

1.1 相对于以太运动的参考系中的光速

设S为以太静止系(简称为静系)，S′系是沿x轴方向以速度v相对于以太匀速直线运动的参考系(简称为动系)，动系和静系之间的坐标变换是伽利略变换(略去了z坐标的变换)

(1)

用时间坐标去除空间坐标即得牛顿速度相加公式

(2)

现在计算动系(S′系)中的光速：

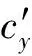
(3)

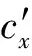
即得到动系中±y′方向的光速其大小是

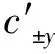
(4)

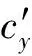
图1 S′系(动系)中的横向光速

1.2 使用1.1给出的S′系中的光速计算迈克耳孙-莫雷实验的条纹移动

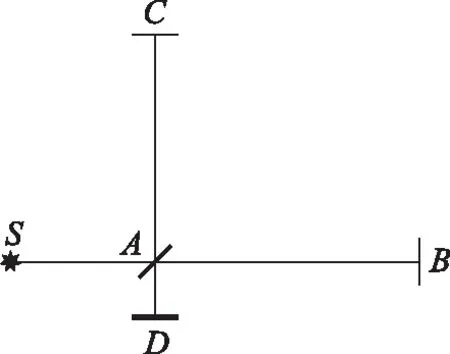
图2 光源S的一束光线，经半透镜A分成两束光，水平光束被反射镜B反射回到A；垂直光束被反光镜C反射回到A,两束反射回的光束经半透镜A投射到观测屏D上形成干涉条纹

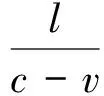
(5)

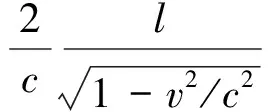
(6)

两束光波从A出发在各自走过往返路径回到A相遇后的时间差则是

(7)

干涉仪在图2 所示的平面内转动90°后两个干涉臂的方向互换，所以转动后的两束光波在A处再相遇后的时间差是

(8)

则转动前后两束光波时间差的改变量δt是

(9)

相应的干涉条纹移动量Δ则是

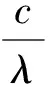
(10)

1887年，迈克耳孙和莫雷的干涉仪臂长11m，光波的波长是5.9×10-7m，如果以太风的速度是地球绕太阳运行的轨道速度30km/s，那么按照静止以太理论的预言干涉条纹移动量Δ≃0.37；但是他们把干涉仪转动90°时发现最大的条纹移动量小于0.01，半年之后地球相对于太阳的运动方向反向了，这时再次实验仍然没有观察到条纹移动，按照实验精度给出的结论是：如果存在以太风的话，那么以太风的速度小于4.7km/s，因而他们的干涉仪观测不到这么小的以太风的效应。

在狭义相对论诞生之后，物理学家们进行过多次类似实验寻找以太的踪迹，精度越来越高，但都是零结果。虽然普遍认为光是一种独立的物质存在而不需要传播媒介，即以太的引入是多余的(当然这只是一种学术观点，不能说以太实验证明了以太不存在，因为实验只能证明“有”，不能证明“无”)； 但是在后来众多的实验文章中之所以仍然使用以太漂移的速度上限表达实验结果，是为了对这类实验的结果精度进行的互相比较。

2 静止以太说+洛伦兹收缩假说对零结果的解释

2.1 洛伦兹收缩假说

干涉仪在以太中静止的时候(即静止在参考系S系的时候)其臂长用l0表示，在动系(S′系)中的干涉仪其横向(y′方向)的臂长不变即仍然是l0，而水平方向(x′方向)的臂长缩短成了l：

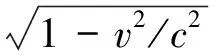
(11)

这就是洛伦兹长度收缩假说：相对于以太运动的物体其运动方向的长度按照方程(11)比它静止在以太中的长度缩短了。

2.2 静止以太说+洛伦兹收缩假说对零结果的解释

在静止以太理论的计算中添加上洛伦兹长度收缩假说后，干涉仪的水平光束与垂直光束在A处重新回合后的时间差由式(7)改写成

(12)

把式(12)中的水平方向的臂长l用式(11)换成l0后得到

Δt0=tABA-tACA=0

(13)

干涉仪转动90°后的时间差仍是零

Δt2π=tABA-tACA=0

(14)

因而转动90°后两束光的时间差没有变化

δt=Δt0-Δt2π=0

(15)

即干涉条纹的移动量Δ=0。

方程(7)称为洛伦兹长度收缩假说(相对于静止以太运动的杆子其长度沿运动方向缩短；在洛伦兹之前斐兹杰惹曾提出过，所以后来有作者把这个假说叫做斐兹杰惹-洛伦兹长度收缩假说[1]；这里简称为洛伦兹长度收缩)。

2.3 洛伦兹的长度收缩与狭义相对论的长度收缩之间的本质差别

方程(7)的洛伦兹收缩与狭义相对论的长度收缩形式相同，但是物理概念完全不同；这里静止在动系S′中的杆子其长度是在相对于杆子静止的条件下度量的，即杆子与观测者相对静止；但是狭义相对论的长度收缩是同时测量运动的杆子两端给出的结果，即杆子相对于观测者是运动的。而且，虽然两种长度收缩公式中都有光速出现，但是式(7)中的光速是指静止以太中的光速，而狭义相对论长度收缩公式中的光速则是光速不变原理中的光速(即任意惯性系中的真空光速)；而且式(7)中的v是由牛顿绝对同时性定义的。

3 双程光速各向同性对零结果的解释

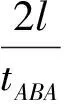
例如使用如下的方程式计算两束光波往返的时间差

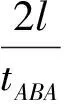
使用式(16)计算的AB方向的光波往返时间是

(18)

使用式(17)计算出的AC方向的光波往返时间是

(19)

所以两束光波往返时间差是

(20)

这就是说只要双程光速各向同性(即cABA=cACA)无论单向光速如何(即无论方向性参数q和q′的数值如何)，式(20)给出的两束光波的往返时间差都是零(即Δt0=0)；转动90°后这个时间差不会变化因而不会有干涉条纹移动。

4 迈克耳孙-莫雷实验对狭义相对论的建立所起的作用

爱因斯坦建立狭义相对论的过程中主要是探讨电动力学的对称性问题，也就是电动力学方程的相对性原理问题，因此他把狭义相对论的第一篇论文[2]叫做“论动体的电动力学”；文中在分析了麦克斯韦电动力学的对称性问题之后说：“……企图证实地球相对于‘光媒质’运动的实验失败，引起了这样一种猜想：不仅在力学中而且在电动力学中，也没有任何现象的特性和绝对静止的观念相对应，倒是应该认为，凡是在力学方程适用的一切坐标系中，也适用着同一的电动力学定律和光学定律……我们要把这个猜想(它的内容以后就称之为‘相对性原理’)提升为假设，并且要引进另一条只在表面上看来同它不相容的假设：光在真空中总是以一个确定的速度V传播着，这个速度同发射体的运动状态无关。……‘光以太’的引用将被证明是多余的。……这里所要阐明的理论……都是关于‘刚体’(坐标系)、时钟和电磁过程之间的关系。”

爱因斯坦的这些陈述指出，早就有了力学的相对性原理(即力学现象不存在绝对静止的参考系也就不存在绝对静止和绝对运动)，但是还没有电动力学的相对性原理；寻找光以太的各类实验的失败使他确认对于电动力学和光学也像力学那样不存在绝对参考系因而假设相对性原理也适合电动力学定律和光学定律。这就是把力学相对性原理推广到适用于电动力学。

至于光速不变的假设彭加勒早已提出了；彭加勒在1898年发表的“时间测量”的论文中写道：“光具有不变的速度，尤其是它的速度在一切方向上都是相同的，这是一个公设，没有这个公设，就无法量度光速。这个公设从来也不能直接用经验来验证；……”所以爱因斯坦不会不知道彭加勒的这个论述。如果说寻找光以太实验的失败对彭加勒的上述观点的产生或许起了很大作用，那么彭加勒的观点对爱因斯坦提出光速不变原理所起到的影响远比光以太实验的影响直接得多和大得多。

即便是有了相对性原理和光速不变原理也不一定能够建立狭义相对论：彭加勒发现了光速不变原理，洛伦兹发现了形式相同的“洛伦兹变换”，但是他们都没有发现狭义相对论。

这是为什么？下面洛伦兹对爱因斯坦相对论的评论可以说明问题。

洛伦兹在1928年的论文中这样评价爱因斯坦的相对论[3]：“相对论实际上完全是爱因斯坦的工作。因此毫无疑问，即使所有前人在此领域的理论工作根本不曾做过，爱因斯坦也会想到它的。在这方面他的工作是与以前的各种理论无关的。”

爱因斯坦在这方面的工作与以前的各种理论无关！也就是说，狭义相对论与以前的各种理论极不相同：在以前的各种理论中，时间的定义都是牛顿的绝对时间，也就是绝对同时性的定义；而狭义相对论中的时间是用不变光速的假设定义的。同时性定义是爱因斯坦建立狭义相对论的关键一步[4]，所以在他1905年第一篇狭义相对论的论文中把同时性定义放在第一部分的第一小节。彭加勒和洛伦兹之所以没有发现狭义相对论也正是由于他们没有对牛顿的绝对同时性定义进行修改。

检验光以太的实验类型很多，例如恒星光行差实验、马司卡脱-贾明以太漂移实验、艾利静止水的以太风实验、菲索流动水实验，以及迈克耳孙-莫雷实验等等都没有观测到以太的效应；虽然这些“企图证实地球相对于‘光媒质’运动的实验失败”促使爱因斯坦提出了狭义相对性原理。但是，迈克耳孙-莫雷实验测量的是光波的往返(双程)时间，不需要定义同时性，也就不可能对建立狭义相对论的关键一步——用不变光速的假设定义同时性[3]起到什么作用。然而，在后来的很多有关狭义相对论的书籍和文章中为何在众多的寻找光以太的实验中单单把迈克耳孙-莫雷实验挑出来作为爱因斯坦建立狭义相对论的重要基础其原由既无据可查也不合理。

[1] 柏格曼P G.相对论引论[M].北京：人民教育出版社，1961：29.

[2] 爱因斯坦.论动体的电动力学[J]//德国《物理学记事》第四系列，1905(17):891-921.

(中译文参见上海人民出版社1973年出版的《爱因斯坦论著选编》第1-22页)

[3] Lorentz H A. Conference on the Michelson-Morley experiment held at mount Wilson[J]. Astrophys J, 1928, 68: 350. (中译文参见科学出版社1980年出版的罗瑟W G V.《相对论导论》第69页)

[4] 张元仲.爱因斯坦建立狭义相对论的关键一步——同时性定义[J].物理与工程，2015，25(3):3-8.

Zhang Yuanzhong. A key step in the development of the special relativity by Einstein-definition of simultaneity[J]. Physics and Engineering， 2015， 25(3): 3-8.(in Chinese)

DIDTHEMICHELSON-MORLEYEXPERIMENTPLAYANIMPORTANTROLEONTHEESTABLISHMENTOFSPECIALRELATIVITY?

WANGXinyi1CHENWanying1ZHANGYuanzhong2

(1Beijing Chenjinglun High School, Beijing 100020;2Institute of Theoretical Physics, Chinese Academy of Sciences，Beijing 100190)

In this paper, the Michelson-Morley experiment is explained by use of three hypotheses: stationary ether hypothesis, stationary ether hypothesis+Lorentz contraction, and the isotropy of the two-way speed of light. Then we analyze the role of the looking for light ether experiments (including the Michelson-Morley experiment) on the establishment of Einstein’s special relativity.

Michelson-Morley experiment; stationary ether hypothesis; Lorentz contraction; the isotropy of the two-way speed of light

2017-08-24

张元仲，男，研究员，主要研究领域是相对论、引力物理与宇宙学，著有专著《狭义相对论实验基础》，zyz@itp.ac.cn。

王欣懿,陈婉盈,张元仲. 迈克耳孙-莫雷实验对狭义相对论的建立起到重要作用了吗？[J]. 物理与工程，2017，27(6)：37-40,44.

■