欧拉-拉格朗日方程在一维波动方程中的应用

王 颖 史旭光

(北京林业大学理学院，北京 100083)

欧拉-拉格朗日方程在一维波动方程中的应用

王 颖 史旭光

(北京林业大学理学院，北京 100083)

本文以一维弦上微元的动能和势能为基础，推导出了一维波动方程。文章首先介绍了通过力学分析得到一维波动方程的方法。然后分析了一维自由运动粒子的动能和势能，引入系统的哈密顿量和拉格朗日函数，由最小作用原理得到了欧拉-拉格朗日方程，也就是粒子的运动方程。将这一方法用于分析一维弦上波动，给出微元的拉格朗日密度函数，得到可以描写无穷多自由度系统的欧拉-拉格朗日方程，从而导出了一维波动方程。最后分析了一维弦上波动的拉格朗日密度与弦理论中Polyakov作用量中的拉格朗日密度的关系。

波动方程；拉格朗日函数；最小作用量原理；欧拉-拉格朗日方程

波动是物理学中的重要概念。人们一般采用动力学、运动学或者叠加原理等方法得到一维波动方程[1-3]，而这些方法中很少有通过能量得到波动方程。本文先介绍从一维弦受力分析得到一维波动方程的方法，然后给出一维粒子拉格朗日函数，并根据最小作用量得到欧拉-拉格朗日方程。通过分析一维弦上微元的动能和势能，给出一维弦上波动的拉格朗日密度函数，从欧拉-拉格朗日方程推导波动方程。

1 一维波动方程力学推导

一维波动方程的推导可由一维弦上微元受力分析得到。考虑一根张紧的弦，弦的一端是振源，当振源简谐振动时，便会有波在弦上传播。如图1，在此弦上选取一段微元dx[4]，微元dx两端的张力分别为T1,T2，T1和水平方向的夹角为θ+dθ，T2与水平方向的夹角为θ。由于微元在水平方向不发生位移，因此水平方向受力平衡

T1cosθ+dθ-T2cosθ=0

(1)

图 1

微元dx在竖直方向有位移，竖直方向受力分析为

(2)

其中ρ是弦的密度。因为dθ很小，根据方程(1)，可以得到条件T1≈T2=T。因此，方程(2)变成

(3)

化简得出波动方程为

(4)

其中u为弦上波速，满足

(5)

2 一维粒子的欧拉-拉格朗日方程

考虑一个粒子在一维空间运动的情况。假设t=0时粒子在x1处，在t时刻粒子在x2处，且满足边界条件

xt1=x1

(6)

xt2=x2

(7)

(8)

(9)

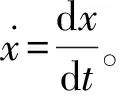
(10)

对此作用量进行变分，结合最小作用量原理[5,6]有

(11)

因为对于任意的δx式(11)都成立，所以式(11)的括号内一项必须为零，即

(12)

此式即为粒子在一维空间运动的欧拉-拉格朗日方程。

3 一维弦上波动的欧拉-拉格朗日方程

考虑到一维弦上波动时，上述一维运动粒子的欧拉-拉格朗日方程需要修改。原因在于一维粒子其自由度只有x和t。而一维弦作为波传播的介质，是一个连续的质点系统，质点和质点之间存在相互作用。当波在一维弦上传播时，是弦上所有质点进行集体运动的结果，其自由度是无穷多的。为了能描述这一质点系系统，需要引入拉格朗日密度函数

L=Lφx,∂μφx,xμ

(13)

其中φ是波函数，描述波动。xμ,μ=0,1是时空坐标，代表t,x。拉格朗日量L与拉格朗日密度函数L满足下式

(14)

由拉格朗日密度函数，推得系统的作用量为

(15)

其中dx2=dxdt为具有边界的二维时空体积R的体积元。当坐标xμ做以下微小的变换

(16)

作用量式(15)的变化为

(17)

考虑到式(16)，有dx′2=1+∂μδxμdx2。可得

(18)

此处δL为

(19)

结合式(18)和(19)，有

(20)

由于

(21)

式(20)变为

(22)

上式第二项来自于斯托克斯公式，∂R是二维时空体积R的边界。在边界∂R上，有δφ=0,δxμ=0。因此，欧拉-拉格朗日方程为

(23)

以上过程可以推广到任意维度，系统的运动方程都是(23)式。

4 由欧拉-拉格朗日方程推导一维波动方程

对于一维弦上的波动，微元在y方向上振动，波沿x方向上传播，坐标xμ代表t,x，此时μ=0,1。我们使用y来表示波函数φ。为了得到拉格朗日密度函数，首先考虑在x处的微元dx的动能，微元dx的动能表达式较为简单，可写为

(24)

微元dx的势能较复杂，可由功能关系推得。微元dx在x方向所受合力为零，没有位移，因此在x没有形变。微元dx的弹性形变产生在y方向上，此方向上的形变记为dy[7]。形变后的微元dx的长度变为

(25)

由此得到由于弦的形变微元dx产生的伸长量为

(26)

也即

(27)

(28)

此功转化为微元dx所具有的势能Ep。考虑到式(7)，微元dx的势能为

(29)

由动能式(24)和势能式(29)，描述微元dx的拉格朗日函数为

(30)

由此可以得到一维弦上的波动的拉格朗日密度为

(31)

参考式(23)，则欧拉-拉格朗日方程变为

(32)

将拉格朗日密度函数式(30)代入此欧拉-拉格朗日方程，得到一维弦上波动方程

(33)

5 讨论

为了给出拉格朗日密度函数式(31)更简洁的表示，定义新坐标

u0=ut,u2=x

(34)

同时引入矩阵

(35)

使用式(34)和式(35)可以得到微元dx的拉格朗日密度函数的

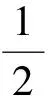
(36)

(37)

此式是平直时空条件下，弦理论polyakov作用量[8]中定义的拉格朗日密度函数。

通过拉格朗日密度函数的方法推导一维波动方程可以使我们更加深入地理解一维弦上波动方程与波的动能和势能的联系。从拉格朗日密度函数出发研究一维弦上波动的问题，不仅可以得到波动方程，还可以给出一维弦上波动问题的哈密顿量，研究一维弦上波的能动张量及各种对称性问题。这正是用拉格朗日方法研究波动问题的优势所在。

[1] 郑承民.用微元思想推导一维波动方程[J].数学学习与研究.2015(03):134-136.

Zheng Chengmin. Deduce one-dimension wave equation by infinitesimal method[J]. Mathematics Learning and Research, 2015(03): 134-136. (in Chinese)

[2] 程守洙,江之永.普通物理学[M].6版.北京：高等教育出版社, 2006:2-4.

[3] Gauthier N,俞志毅.一维波动方程的推导[J].大学物理,1989(12): 45.

Gauthier N, Yu Zhiyi. Deducing the expression of one-dimensional wave equation[J]. College Physics, 1989(12): 45.(in Chinese)

[4] 吴宗试.数学物理方法[M].北京：北京大学出版社,2003.

[5] 段一士.量子场论[M].北京:高等教育出版社,2015:38.

[6] Ryder L H. Quantum field theory[M].2版.Cambridge:世界图书出版公司,1996:80-84.

[7] 郭芳英，闫夷升，李爱玲.用横波推导简谐波的能量[J].物理与工程，2003,12(2):16-17.

Guo Fangying, Ran Yisheng, Li Ailing. The energy in simple harmonic waves for transverse wave[J]. Physics and Engineering, 2003, 12(2): 16-17.(in Chinese)

[8] MacMahon D. String theory demystified[M]. New York: McGraw-Hill Companies, 2009, 36.

APPLICATIONOFEULER-LAGRANGEEQUATIONINONE-DIMENSIONALWAVEEQUATION

WANGYingSHIXuguang

(College of Science, Beijing Forestry University, Beijing 100083)

In this paper, the one-dimensional wave function is studied in frame of the kinetic energy and potential energy. In general, one-dimensional wave equation is obtained through the force analysis of an arbitrary string element and Newton’s second law. In this paper, we introduce the Lagrangian of a particle, which moves in the potentialV. Then Euler-Lagrange equation, Which is also the motion equation of particle, is given based on the principle of the least action. In the frame of this theory, we give the kinetic energy and potential energy of the string element. Then the Lagrange density function of the 1-dimension string element is defined. The Euler-Lagrange equation to describe a system with infinite degrees of freedom is obtained. Based on these, the one-dimensional wave equation is revealed. At last, we give the relations between Lagrange density function in one-dimensional wave and Lagrange density function in Polyakov interaction in string theory.

wave equation; Lagrangian function; principle of least action; Euler-Lagrange equation

2016-11-09;

2017-05-16

中央高校基本科研业务费专项资金资助(2015ZCQ-LY-02)。

史旭光，男，副教授，主要从事大学物理教学和拓扑场论的研究，shixg@bjfu.edu.cn。

王颖,史旭光. 欧拉-拉格朗日方程在一维波动方程中的应用[J]. 物理与工程，2017，27(6)：41-44.

■