“几何”那些事儿
许天枢
几何是什么东东?
直观地说,与图形有关的数学内容就是几何.
抽象地说,数学是研究数量关系(简称“数”)和空间形式(简称“形”)的学科,其中以空间形式为直接研究对象的分支,叫做几何.
几何从哪里来?
当然从生活中来,因为需要,所以创造嘛!
根据史料和实证,古埃及时代,尼罗河水定期泛滥,淤积的泥土经常冲毁两岸土地,水退后土地的界限常常面目全非,当时劳动人民为了重新测出被洪水淹没的土地边界,每年都要进行土地测量,长此以往,积累了许多测量土地方面的经验和知识.几何就起源于测量土地的技术,几何学的英文单词geometry就是由geo(土地)和metry(测量)组成的,另外,制造器皿、测量容器等都是几何起源的摇篮.明代,徐光启和利玛窦将geometry翻译成“几何”,在汉语中是“多少”的意思,你瞧,用数量刻画图形的形状、位置、大小,含意多么隽永啊!
几何是怎么发展起来的?
几何从当初的萌芽到如今的参天大树,不吹不黑地讲,它的发展历史堪称是一部人类认识世界、改造世界的壮丽史诗.
综合东西方数学的发展来看,几何的发展大致可以分成这样三个阶段:
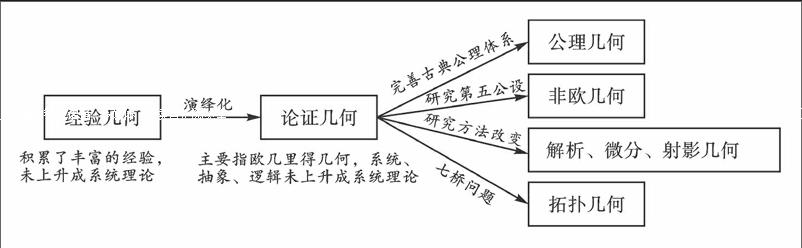
一、几何的萌芽和初步发展——经验几何阶段
远古时代,人们在实践中渐渐感受到丰富的几何概念,比如曲、直、平、圆、大小、长短、宽窄、厚薄、远近,初步有了“形”的意识,进而尝试简单的土地度量、器皿制造等工作,对“几何结构”的探索就慢慢开始了,日积月累,渐渐形成了丰富的几何经验.
例如,大量的出土文物证明,在我国史前时期,人们已经掌握了许多几何的基本知识,出土的陶罐上绘有方格、米字、回文等图案,设计精巧、对称.进一步发展,几何知识逐渐经验化、专业化,如春秋时的著作《考工纪》把几种特殊的角给出了特定的名称,90°的角叫“矩”,45°的角叫“宣”,135°的角叫“磬折”,《周髀算經》提出了勾股定理及其证明,《九章算术》进一步展示了勾股定理如何应用于实践.
所谓经验几何,就是人们“感受体验→归纳概括→应用检验”.其实,这也是我们学习几何的必经之路!经验几何中比较重要的方法是特例研究发现法和不完全归纳法,都是需要我们认真体会和实践的.
二、由哲学而来的几何——论证几何阶段
尽管那时候几何知识已经十分丰富,但这些知识仍然是零散的、孤立的、不系统的.柏拉图和亚里士多德把哲学引入几何,为几何系统化提供了理论依据和思想支柱,而真正把几何总结成一门具有比较严明理论的学科的,是古希腊数学家欧几里得.欧几里得的著作《几何原本》最突出的是从一些特别提出的公理、公设和定义有计划地来论证其他命题,其次是它第一次把丰富而散漫的几何材料整理成了系统严明的读本.正因为如此,他的《几何原本》一直被后世所推崇,以至于两千多年来所有初等几何教科书以及初等几何的论著无不以他的《几何原本》为根据.
所以论证几何的特点就是“系统、严密”,在初中阶段,我们将在证明和说理中体会这些特点.
三、百花齐放的新几何——现代几何阶段
随后,几何出现了百花齐放的局面,笛卡尔将“坐标”引入了几何,从而实现了数形结合,这就是“解析几何”;古希腊依茨都山尼根据几何知识和日光观察,提出了“球面几何”,对地球大小做出了初步估计,这就是后来的“非欧几何”的雏形;希尔伯特在总结前人工作基础上,提出了一个更加完善的几何学公理体系——希尔伯特公理体系,具有“和谐性、独立性、完备性”的特点……再加上“微分几何”“拓扑几何”“射影几何”这些不可忽略的花朵,组成了现代几何阶段的局面.有兴趣的同学不妨去查阅一番,相信你一定会收获满满的!
初中几何学什么?
初中阶段的几何图形既有立体图形,又有平面图形,立体图形涉及不多,主要学的是平面图形(线和角、三角形、四边形、圆)的形状、大小、关系.这里既有直观的观察和感受,也有严密的逻辑推理,充满了“美”和“理”,请大家充满期待吧!
几何就要来了,你准备好了吗?
(作者单位:江苏省南京市第五十中学)endprint

