风储孤网系统小干扰稳定性分析研究*

叶 鹏, 李 山, 何 淼, 王 刚, 韩 月, 孙 峰

(1. 沈阳工程学院 电力学院,辽宁 沈阳 110136;2. 国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006)

风储孤网系统小干扰稳定性分析研究*

叶 鹏1, 李 山1, 何 淼1, 王 刚2, 韩 月2, 孙 峰2

(1. 沈阳工程学院 电力学院,辽宁 沈阳 110136;2. 国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006)

从电力系统运行的一般原理出发，开展风储孤网系统小信号稳定和动态稳定的研究，保障局部地区供电可靠性。基于特征值分析法和李亚普诺夫线性系统稳定性判据，对风储孤网系统小干扰稳定性问题进行了研究。提出风储孤网系统储能单元基于下垂控制模式的储能逆变器控制策略，并根据风储孤网系统各模块的控制策略建立相应的数学模型；基于特征值分析法进行风储孤网系统各模块数学模型的小干扰稳定性分析，并根据李亚普诺夫线性系统稳定性判据进行风储孤网系统的稳定性判断；基于MATLAB/Simulink仿真平台搭建风储孤网系统仿真模型，通过仿真验证了风储孤网系统能够实现稳定运行，与小干扰稳定性分析得出的结论一致。研究成果可为风储孤网系统的运行稳定性研究提供理论参考。

风储孤网系统;下垂控制;小干扰稳定;特征值分析法;李亚普诺夫判据

0 引 言

随着风电产业的快速发展，我国风电装机容量不断增加。然而，受大电网接纳能力的限制，风电大规模接入电网过程中存在“并网难”和“弃风”等问题，成为制约风电发展的重大难题[1-2]。针对上述风电并网难题，国内外专家提出风储联合发电技术。随着储能装置成本的降低和技术的成熟，风储孤网发电技术作为风储联合发电技术的一种有效形式，能够为新能源分散和小规模应用提供较为灵活的运行方式，而逐步受到研究人员的广泛重视。开展风储孤网系统的研究，不仅有利于促进清洁能源技术及储能技术的发展和应用，而且对于解决偏远地区的供电问题、提高电网运行和控制的灵活性有着积极的现实意义。

目前，国内外有关风储联合系统的小干扰稳定性研究主要集中在单一的风力发电系统或者储能系统的小干扰稳定性研究，而对风储孤网系统小干扰稳定性分析的研究较少。文献[3-6]建立风力发电系统的数学模型，并通过特征值分析法对风力发电系统的数学模型进行小干扰稳定性分析，得出了影响风力发电系统稳定运行的若干因素，为风力发电系统的并网稳定运行提供可借鉴的参考。文献[7-8]分析了并网运行的储能逆变器的小干扰稳定性，得出了影响储能逆变器并联运行的主要控制参数，并通过仿真验证了主要控制参数对储能逆变器的小干扰稳定性的影响。文献[9]对风力发电、光伏发电和储能单元组成的混合发电系统进行小干扰稳定性研究，并通过仿真验证了混合发电系统小干扰稳定性分析的正确性。在风储孤网系统中，开展风储孤网系统的小干扰稳定性研究是保障局部地区供电可靠性的关键。

针对风储孤网系统的运行稳定性问题，首先，提出风储孤网系统储能单元基于下垂控制模式的储能逆变器控制策略，并根据风储孤网系统各模块的控制策略建立相应的数学模型；其次，基于特征值分析法进行风储孤网系统各模块数学模型的小干扰稳定性分析，并根据李亚普诺夫线性系统稳定性判据进行风储孤网系统的稳定性判断；最后，基于MATLAB/Simulink仿真平台搭建风储孤网系统仿真模型，通过仿真验证了风储孤网系统能够实现稳定运行，与小干扰稳定性分析得出的结论一致。

1 风储孤网系统结构

风储孤网系统主要由风力发电系统、储能单元和负载组成。与双馈风力发电机组相比，直驱永磁风力发电机组因省去电刷、滑环和齿轮箱，从而大大减少系统的维护费用，提高系统的可靠性[10]。在本文的研究中风电机组采用直驱永磁风力发电机组。风储孤网系统的控制框图如图1所示。直驱永磁风力发电系统主要由风力机、直驱永磁风力发电机、机侧整流器、网侧逆变器和滤波装置组成；储能单元主要由蓄电池、DC/DC双向变流器、储能逆变器和滤波装置组成。直驱永磁风力发电机与储能单元共同经过交流母线向负载供电。

图1 风储孤网系统的控制框图

风储孤网系统工作过程如下：风力机从自然风中捕获最大机械功率，并将产生的机械功率通过主轴传送给发电机组，发电机组发出的电经过背靠背变流器控制电路和滤波装置向负载供电；而储能单元通过采集交流母线侧电压和电流信号来控制储能逆变器的各桥臂的通断以达到抑制因风速的突变而导致的风电输出功率的波动。同时，储能单元还可以作为备用电源，当风电出力过大时，储能单元可以吸收风电发出的多余功率；当风电出力过小时，储能单元可以输送存储的功率向负载供电。

2 风储孤网系统数学模型

2. 1 风力机数学模型

风力机将风能转化成机械功率。风力机产生的机械功率为：

(1)

式中：ρ——空气密度；

r——风轮机半径；

Cpmax——最大风能利用系数；

λopt——最佳叶尖速比；

wg——风机机械角速度。

风机机械转矩Tm为

(2)

风机机械运动方程为：

(3)

式中:Te——发电机电磁转矩，Te=1.5pφiqs；

p——发电机极对数；

φ——永磁体磁链；

iqs——定子电流q轴分量；

TJ——风机系统总转动惯量。

2. 2 永磁风力发电机数学模型

在dq坐标系下，永磁风力发电机的数学模型为

式中：uds、uqs——定子电压d、q轴分量；

ids、iqs——定子电流d、q轴分量；

φ——永磁体磁链；

wg——机械角速度；

Rs、Ls——定子电阻和电感。

2. 3 发电机侧整流器控制数学模型

图2 发电机侧整流器控制结构图

发电机侧整流器控制的数学模型为：

(6)

式中:x1、x2、x3——中间变量；

kp1、kp2、kp3——3个PI控制器的比例系数；

ki1、ki2、ki3——3个PI控制器的积分系数；

ids、iqs——定子电流d、q轴分量；

Ls、Rs——定子电感、定子电阻；

wg——风机转速；

uds、uqs——定子电压d、q轴分量。

2. 4 网侧数学模型

网侧逆变器控制结构图如图3所示。网侧滤波电路主要是滤除谐波。在dq坐标系下网侧滤波电路数学模型为：

(11)

式中：ugd、ugq——网侧逆变器端口输出电压的d、q轴分量；

igd、igq——网侧逆变器经过滤波装置之后输出电流的d、q轴分量；

Lg、r——网侧滤波电感和电阻；

U0d——交流母线上的电压的d轴分量；

w——交流母线上电压对应的角频率。

网侧逆变器的主要作用是实现网侧功率因数调整或无功功率控制，提供稳定的直流电压控制，网侧逆变器采用电压外环和电流内环的控制策略。网侧逆变器控制的数学模型为

式中:x4、x5、x6——中间变量；

kp4、kp5、kp6——3个PI逆变器控制的比例系数；

ki4、ki5、ki6——3个PI控制器的积分系数；

udc——直流侧电容两端的实际电压；

Lg——网侧滤波电感；

w——交流母线上电压对应的角频率。

图3 网侧逆变器控制结构图

2. 5 直流侧电容数学模型

整流器和逆变器之间的直流侧电容的主要作用是实现发电机侧和网侧之间的能量交换，稳定直流侧的电压并使其具有电压源特性。直流侧电容数学模型为[11]

(17)

式中:ids、iqs——定子电流d、q轴分量；

igd、igq——逆变器经过滤波电感之后输出电流的d、q轴分量；

C——整流器和逆变器之间的电容；

udc——整流器和逆变器之间的电容两端的电压；

uds、uqs——定子电压d、q轴分量；

ugd、ugq——网侧逆变器端口输出电压的d、q轴分量。

2. 6 储能单元数学模型

储能单元中，双向储能逆变器进行双向有功功率交换的控制和交流母线电压的控制。为简化研究本文只对储能逆变器的小干扰稳定进行分析。本文中储能逆变器采用下垂控制模式。储能逆变器下垂控制模式的控制框图如图4所示。储能单元中储能逆变器网侧LC滤波电路在dq坐标系下的数学模型为：

(18)

图4 储能逆变器下垂控制模式控制框图

式中:U0d、U0q、i0d、i0q——储能逆变器中经LfCf滤波输出的三相电压U0abc、三相电流i0abc通过abc/dq0变换后的得到的电压和电流的d、q轴分量；

w——交流母线上电压对应的角频率；

rf、Lf——电阻和滤波电感；

Cf——滤波电容；

Ud、Uq、id、iq——储能逆变器输出的三相电压Uabc和三相电流iabc通过abc/dq0变换后的得到的电流的d、q轴分量。

储能逆变器下垂控制模式的数学模型如下：

储能逆变器输出瞬时有功功率和无功功率的方程为

(20)

瞬时功率经过一阶低通滤波器可以得到平均功率为

(21)

式中:U0d、U0q、i0d、i0q——储能逆变器中经LfCf滤波输出的三相电压U0abc、三相电流i0abc通过abc/dq0变换后的得到的电压和电流的d、q轴分量；

wc——截止角频率；

P、Q——平均有功功率、平均无功功率。

储能逆变器输出电压频率和幅值的下垂特性方程为

(22)

式中：w0、E0——储能逆变器输出的额定角频率、额定电压；

mp、nq——有功下垂系数、无功下垂系数；

P、Q——储能逆变器实际输出的平均有功功率、平均无功功率；

Pref、Qref——储能逆变器参考有功功率、无功功率。

储能逆变器在经过下垂控制之后需经过电压外环和电流内环的双环控制策略。电压外环和电流内环的控制策略如图5所示。

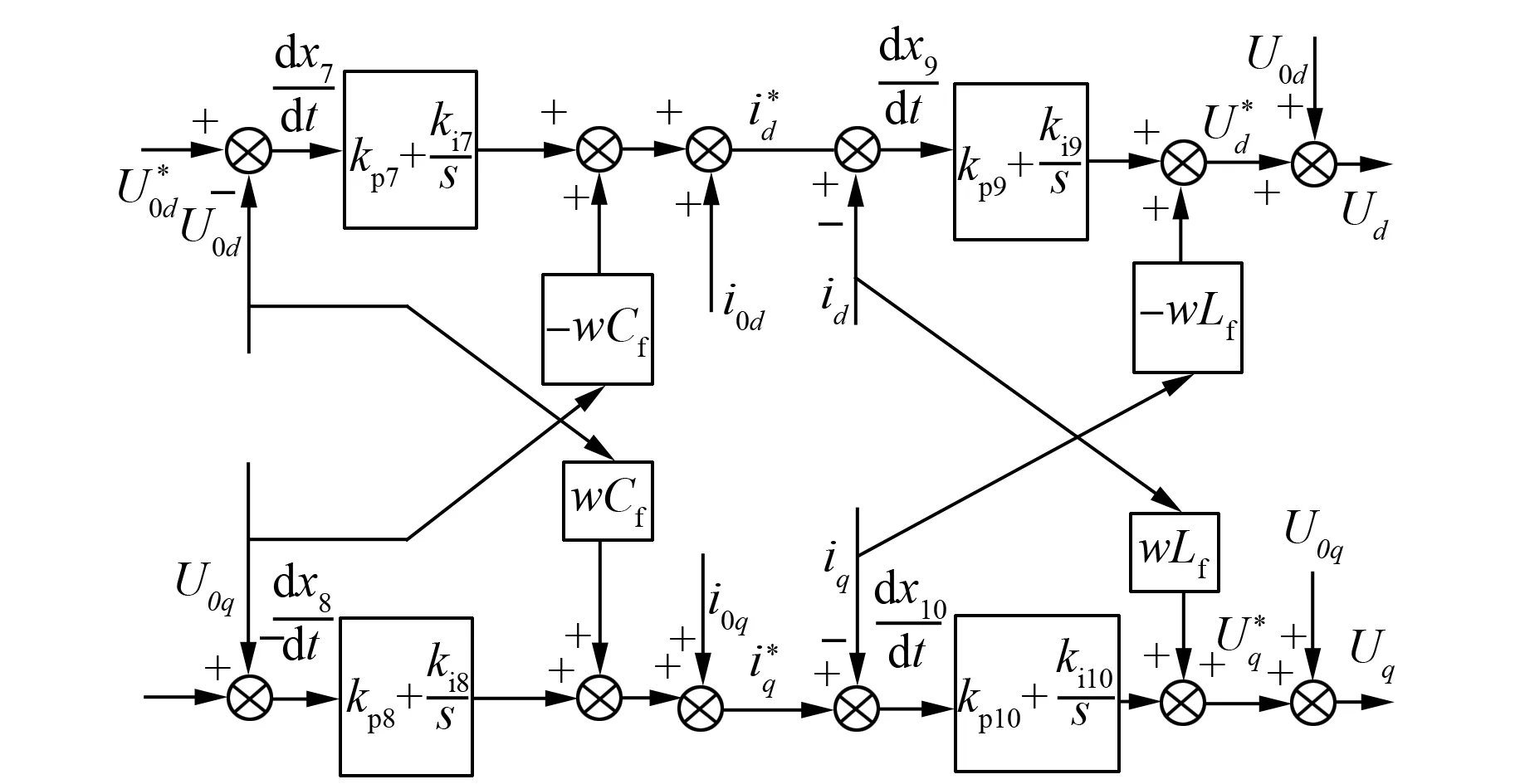
图5 电压外环和电流内环的控制策略

电压外环和电流内环控制的数学模型为

(23)

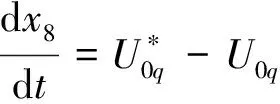
Ud、Uq——储能逆变器输出的三相电压Uabc通过abc/dq0变换后的得到的电流的d、q轴分量；

x7、x8、x9、x10——中间变量；

kp7、kp8、kp9、kp10——4个PI控制器的比例系数；

ki7、ki8、ki9、ki10——4个PI控制器的积分系数；

id、iq——储能逆变器输出的三相电流iabc通过abc/dq0变换后的得到的电流的d、q轴分量；

w——交流母线上电压对应的角频率；

Lf——滤波电感，

Cf——滤波电容；

U0d、U0q、i0d、i0q——储能逆变器中经LfCf滤波输出的三相电压U0abc、三相电流i0abc通过abc/dq0变换后的得到的电压、电流的d、q轴分量。

储能单元中，储能电池采用铝离子电池，储能电池的充放电模型以及剩余电量(SOC)的表达式为

式中：Edisc——放电电压；

Ec——充电电压；

E0——参考电压；

K——极化常数；

Q——蓄电池最大容量；

it——可提取的电能；

i*——低频参考电流；

i(t)——低频动态电流；

A——指数电压；

B——指数容量。

3 系统小干扰稳定性分析

电力系统运行稳定性分析常用的方法主要有：特征值分析法、数值仿真法、频域分析法和Prony分析方法。本文采用特征值分析法进行风储孤网系统小干扰稳定性分析。小干扰稳定性分析的特征值分析法的相关理论可参考文献[12]。

对式(3)～式(30)进行小干扰稳定线性化分析和化简，可得出风储孤网系统小干扰稳定线性化方程为

式中:wg(0)、uds(0)、ids(0)、uqs(0)、iqs(0)、ugd(0)、igd(0)、w(0)、wc(0)、iod(0)、ioq(0)、Uoq(0)、Uod(0)——相关变量的稳态值。

则风储孤网系统小干扰稳定线性化矩阵方程可表示为

(56)

其中：x=[ids,iqs,wg,x1,x2,x3,igd,igq,x4,x5,x6,Udc,P,Q,id,iq,U0d,U0q,x7,x8,x9,x10]T

由式(34)～式(55)可得，风储孤网系统小干扰稳定线性化矩阵A为

(57)

a19,14=-nq，a19,17=-1，a20,18=-1，a21,13=mpCfU0q,a21,14=-kp7nq，a21,15=-1，a21,17=-kp7，a21,18=-wCf，a21,19=ki7，a22,13=-mpCfU0d，a22,16=-1，a22,17=wCf，a22,18=-kp8，a22,20=ki8；矩阵中其他相关元素为0。

3. 1 系统稳定性分析

根据李亚普诺夫线性系统稳定性判据可知：当矩阵的特征值全部位于s平面的左半部分，即所有的特征值的实部均为负时，系统处于稳定运行状态；当矩阵的特征值有部分或者全部位于s平面的右半部分，即部分或者全部的特征值的实部为正时，系统运行不稳定。因此，在进行风储孤网系统稳定性分析的过程中，可以根据风储孤网系统小干扰稳定线性化矩阵的所有特征值在s平面的分布情况来判断系统是否稳定。

利用上文建立的风储孤网系统的小干扰模型，判断风储孤网系统算例的小干扰稳定性。某一运行状态下的风储孤网系统算例参数的选取如表1所示。

将表1中的系统参数代入式(57)，得到风储孤网系统小干扰稳定线性化矩阵的特征根在实轴和虚轴的分布如图6所示。由图6可知，风储孤网系统算例的小干扰稳定线性化矩阵的特征根均分布在s平面的左半部分，由李亚普诺夫线性系统稳定性判据可知，风储孤网系统处于稳定运行状态。

3. 2 仿真分析

按照图1中的风储孤网系统的控制框图进行系统仿真模型的搭建。设额定风速为12 m/s，风机输出额定功率为25 kW，交流母线侧的负载功率为30 kW，蓄电池荷电状态的初始值为80%，其余控制参数可参考表1。则风储孤网系统的仿真图如图7～图12所示。

由图7～图12可知，交流母线侧的负载有功功率为30 kW，而风电机组输出的额定功率为25 kW，在风电机组输出有功功率不能满足交流负载的情况下，为了维持系统的有功功率平衡，蓄电池储能系统通过自身放电向交流负载提供5 kW的有功功率。在系统稳定运行的过程中，交流母线上的三相电压和频率均满足风储孤网系统交流负载的需求。从仿真分析可知风储孤网系统能够实现稳定运行。

表1 风储孤网系统算例的参数选取表

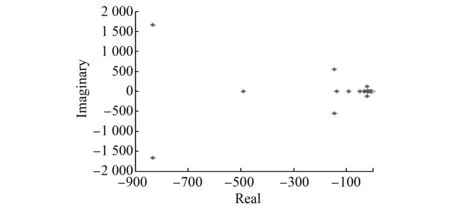
图6 系统小干扰线性化矩阵特征根分布

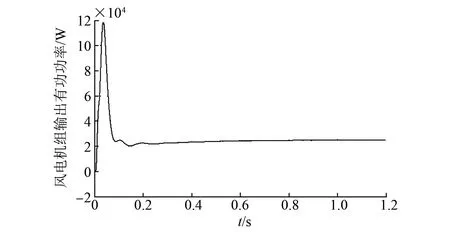
图7 风电机组输出有功功率

图8 负载有功功率

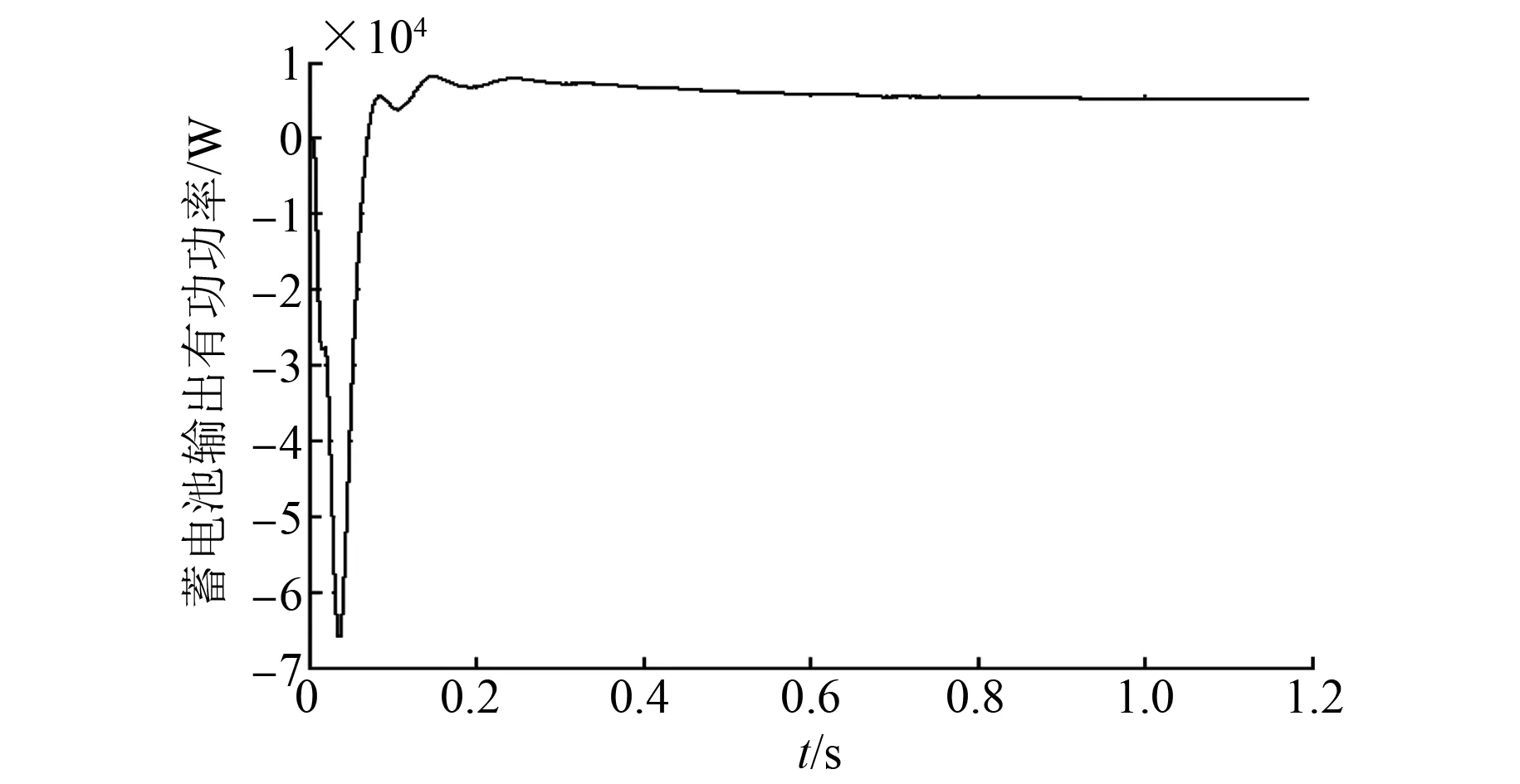
图9 蓄电池输出有功功率

图10 交流母线侧三相电压

图11 蓄电池荷电状态

图12 交流母线侧频率

4 结 语

基于特征值分析法和李亚普诺夫线性系统稳定性判据，本文对风储孤网系统的运行稳定性问题展开了深入的研究，主要研究内容如下：

(1) 提出了风储孤网系统各模块的控制策略，其中储能单元采用基于下垂控制模式的储能逆变器控制，根据各模块的控制策略建立了相应的数学模型；基于特征值分析法进行风储孤网系统各模块数学模型的小干扰稳定线性化分析，并根据李亚普诺夫线性系统稳定性判据完成风储孤网系统运行稳定性的判断。

(2) 在完成风储孤网系统运行稳定性的判断之后，基于MATLAB/Simulink仿真平台搭建风储孤网系统仿真模型，并进行风储孤网系统的仿真分析。仿真分析验证了风储孤网系统能够实现稳定运行，与小干扰稳定性分析得出的结论一致。仿真结果从侧面验证了基于特征值分析法和李亚普诺夫线性系统稳定性判据在分析风储孤网系统的运行稳定性问题上的有效性。本文的研究成果可为风储孤网系统的运行稳定性问题的进一步研究提供理论参考。

[1] VRETTOS E I, PAPATHANASSIOU S A. Operation policy and optimal sizing of a high penetration RES-BESS system for small isolated grids[J].IEEE Transactions on Energy Conversion,2011,26(3): 744-756.

[2] SOUZA R L A, SAAVEDRA O R, LIMA S L, et al. Isolated micro-grids with renewable hybrid generation: The case of Lencois island[J].IEEE Transactions on Sustainable Energy,2011,2(1): 1-11.

[3] 杨昆,杨秀.基于小扰动稳定性分析的并网直驱永磁风电系统建模优化和仿真[J].华东电力,2014,42(9): 1796-1801.

[4] 李军军,吴政球,谭勋琼.下垂控制对直驱永磁风力发电系统的小扰动稳定影响[J].中国电机工程学报,2011,31(3): 52-59.

[5] 刘严,袁越,傅质馨.直驱永磁风电场并网运行的小干扰稳定性分析[J].电力系统及其自动化学报,2012,24(5): 1-6.

[6] 李军军,吴政球,谭勋琼.直驱永磁型风电系统的小扰动稳定性分析[J].电力系统及其自动化学报,2012,24(5): 49-57.

[7] 周丹,赵波,张雪松等.并网运行的储能逆变器小信号稳定性分析[J].浙江电力,2014(1): 1-5.

[8] 张野.微网中电池储能系统控制策略的研究[D].天津:天津大学,2013.

[9] 黄汉奇.风力发电和光伏发电系统小干扰稳定研究[D].武汉:华中科技大学,2012.

[10] 胡书举,李建林,许洪华.永磁直驱风电系统变流器拓扑分析[J].电力自动化设备,2008,28(4): 77-82.

[11] 李军军.并网型风力发电系统的小扰动稳定性分析研究[D].长沙:湖南大学,2011.

[12] 冯闯.永磁风力发电机组小扰动稳定性分析[D].长沙:湖南大学,2013.

ResearchonSmallDisturbanceStabilityofWindStorageIsolatedNetworkSystem*

YEPeng1,LIShan1,HEMiao1,WANGGang2,HANYue2,SUNFeng2

(1. School of Electric Power, Shenyang Institute of Engineering, Shenyang 110136, China;2. State Grid Liaoning Electric Power Research Institute, Shenyang 110006, China)

Based on the general principle of power system operation, the study of the small signal stability and dynamic stability of the wind storage isolated network system was the key to ensure the reliability of power supply in some areas. Based on the eigenvalue analysis method and the Lyapunov stability criterion of linear system, the problem of small disturbance stability of the wind storage isolated network system was studied. The energy storage inverter control strategy based on droop control mode is proposed, and the corresponding mathematical model was established according to the control strategy of each module of the wind storage isolated network system. Small disturbance stability of mathematical model of each module of the wind storage isolated network system was analysed based on eigenvalue analysis, and the stability judgment of the wind storage isolated network system was determined according to the Lyapunov stability criterion of linear system. Based on the MATLAB/Simulink simulation platform, the simulation model of the wind storage isolated network system was established, and the simulation results showed that the system could achieve stable operation, which was consistent with the small disturbance stability analysis. The research results could provided theoretical reference for the study of the stability of wind storage isolated network system.

windstorageisolatednetworksystem;droopcontrol;smallsignalstability;eigenvalueanalysis;lyapunovcriteria

辽宁省教育厅项目(L2015376); 辽宁省自然科学基金指导计划(201602534)

叶 鹏(1974—)，男，博士，教授，研究方向为电力系统运行与控制，新能源发电及特高压交直流输电技术等。

李 山(1989—)，男，硕士研究生，研究方向为电力系统运行与控制、新能源发电技术。

TM 315

A

1673-6540(2017)12- 0084- 10

2017 -05 -03

引领技术发展趋势 报道经典实用案例 反映行业最新动态