渐开线转子型线的参数化与最优化研究

李玉龙, 冉光泽，张宸赫

(成都大学 机械工程学院，四川 成都 610106)

渐开线转子型线的参数化与最优化研究

李玉龙, 冉光泽，张宸赫

(成都大学 机械工程学院，四川 成都 610106)

为实现罗茨泵渐开线转子副的造型参数化与尺寸最优化，基于渐开线的成形原理，从几何关系、理论型线、取值范围、实际型线和参数化模型等方面，给出实际型线的全参数化坐标方程与3D模型的构建方法；以节圆半径和形状系数为设计变量，转子副所占方体空间的最小体积为目标函数，构建优化模型和实例分析.结果表明，峰圆弧与谷圆弧仅为型线的过渡曲线，并不参与啮合运动；三维模型验证，均能实现零件与装配件的全参数化；容积利用系数的拟合精度高，4阶的多项式拟合能满足设计要求；实例参数下，105 mm节圆半径和1.367形状系数的优化结果，说明转子尺寸优选的必要性.

罗茨泵；渐开线转子；造型参数化；容积利用系数；设计最优化

0 引 言

罗茨泵是一种回转式容积泵，工作原理类似于齿轮泵，具有原理简单、体积小、重量轻、成本低、密封性好与无污染等特点，在鼓风、抽真空与介质输送等方面有着广泛的应用[1-3].其中，多叶转子是罗茨泵的核心部件，其型线设计的好坏，直接决定泵的性能.依据应用场合的不同，转子可采用圆弧、渐开线、摆线、直线、抛物线等多种线型，或彼此间的组合线型[4-5].目前，针对型线造型的研究比较多，但能够真正实现全参数化的却比较少.虽然渐开线被齿轮传动所广泛采用，但在罗茨泵转子上的应用研究却很少，现有的也仅限于给出了型线的理论方程[6-7].另外，转子几何尺寸的确定，会受到诸如旋心距取整、最小谷部尺寸、最大最小转子宽度及最小容积利用系数等多方面的限制，存在着一个设计上的优化问题[8]，但相关文献报道极少.基于此，本研究针对渐开线转子，拟就其实际型线的全参数化方程和转子尺寸的优化设计做进一步的深入研究与分析.

1 几何关系

转子型线分为节圆之内的谷型线和节圆之外的峰型线两类，且两者互为共轭.对渐开线型线而言，其共轭曲线仍为渐开线.设N为转子的叶数，以主动转子旋心o1为原点，谷部对称轴线(简称谷轴)为x轴，构建xo1y坐标系，截取一半完整叶后的几何轮廓如图1所示.其中，δ为转子间的间隙.δ=0时，得到的是转子的理论型线，否则是实际型线.

图1渐开线型线几何关系

渐开线转子的理论型线，由图1中峰圆弧段1、渐开线段2和谷圆弧段3组成.其中，根据啮合传动的需要，峰圆弧段1的圆心on位于节圆和峰轴上，谷圆弧段3的圆心on位于节圆和谷轴上.令，

(1)

式中，φ为转子理论型线所对应的旋心夹角；r为节圆半径；α为节圆压力角；rb为基圆半径；ra为理论峰径；rv为理论谷径；ε为理论形状系数.rn为理论峰弧段1的圆半径.

由渐开线段2在基圆上的纯滚动角也为φ，得峰圆弧段1和谷圆弧段3不参与啮合，这一点与常见渐开线齿轮的齿顶圆弧和过渡曲线段一样.

2 理论型线

转子理论型线上的渐开线段2如图2所示.设点m为其上的任意一点，渐开线段2的起始与终止点为点s与点e；s、m与e三点各自所对应的曲心为os、om与oe；各自所对应的半径为rs、rm与re；各自法线与节圆的交点为ps、pm与pe；各自的压力角与展角为αs与θs、αm与θm、αe与θe.

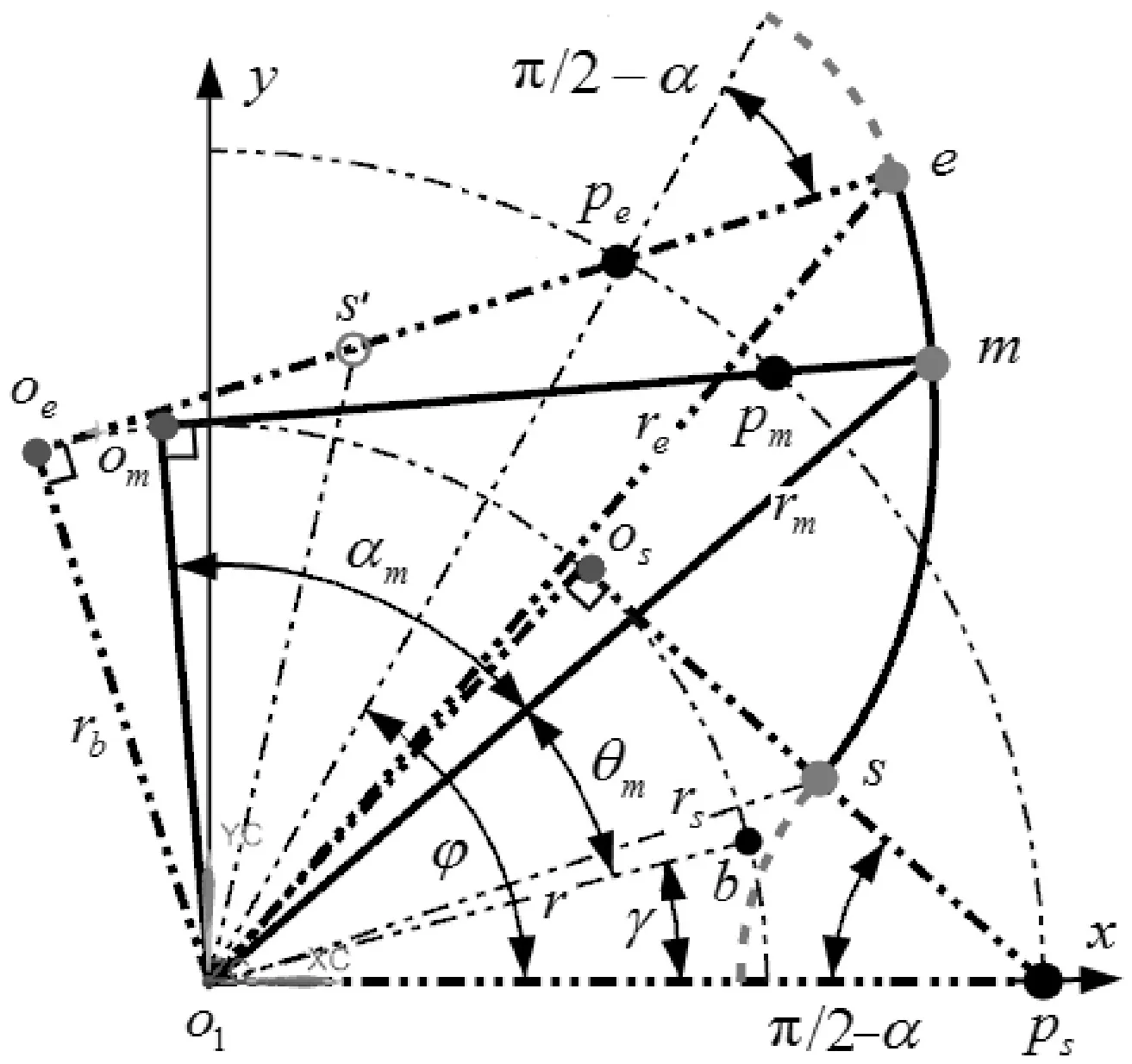
图2转子理论型线示意图

在图2的Δo1pss与Δo1pee中，由各自三边长间的几何关系，整理得，

(2)

由渐开线的形成特点，得，

γ=∠pso1os-∠so1s-∠bo1s

=α-αs-(tgαs-αs)

(3)

式中，γ为渐开线段2在基圆上的对应点b与谷轴所对应的旋心角.其中，

αs=tg-1(tgα-rn/rb)

(4)

由于rm介于rs与re之间，则设，

rm(t)=rs+(re-rs)t

(5)

式中，t为0～1间的变量，并有，

αm(t)=cos-1(rb/rm)

θm(t)=tgαm-αm

(6)

3 取值范围

在图2中，将直角Δo1oss纯滚动到直角Δo1oee位置，设s′为s纯滚动后的新位置，则有，

(7)

式中，“-"表示两点间展开线的长度；“⌒"表示两点间基圆弧的长度，得，

(8)

在图2的直角Δo1osps中，由，

(9)

得，

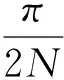
(10)

式中，αmin为α的取值下限.

由δ≪2rb，则，

(11)

式中，εmax为ε的取值上限.

4 实际型线

由于间隙δ的存在，图3中的理论渐开线段2上的任意一点m，将沿着该点处的法线向曲心om偏置0.5δ后到点mδ，该点即为转子实际型线上的任意一点，此时有，

(12)

图3转子实际型线示意图

5 坐标方程

在图1的xo1y坐标系中，设实际峰圆弧段1上任意一点的坐标为(x1，y1)，实际渐开线段2的坐标为(x2，y2)，实际谷圆弧段3的坐标为(x3，y3).有，

(13)

和，

(14)

且，

6 参数模型

能生成实体的截面必须具有封闭轮廓.为此，需再构建出如下的峰轴线和谷轴线的参数化方程，

(16)

式中，(xa,ya)、(xv,yv)分别为峰、谷轴线的坐标方程.

首先，创建峰轴线、实际峰圆弧段1、实际渐开线段2、实际谷圆弧段3和谷轴线的规律曲线[9]；其次，再由它们围成的封闭轮廓，拉伸成半叶实体；第三，在对半叶实体的轴孔除料后，由半叶实体关于由峰轴和z轴生成的面(简称峰轴面)对称成一个整叶实体，再利用整叶的N参数化，圆周阵列出一个完整的转子模型，并插入峰轴面、谷轴面和旋心轴.具体如图4a所示.

图4参数模型示意图

在转子副装配模型中，生成主、从动转子的装配基准面和旋转基准轴，其中，两者之间的距离为2r(见图4b).然后，通过装配的参数化角度的约束关系，生成一对关于旋转角度参数化的转子副[9](见图4c).叶数和δ=1 mm的参数化模型，如图5所示.图5中，实际间隙不可能达到1 mm，这里仅为显示用.

图5 转子副模型示意图

7 优化设计

在优化设计中，改设轴径为0.00001 mm，将区间[1,εmax]9等分后，采用三维软件的面积测量工具，测出形状系数ε分别为这些等分点下的转子截面积，然后计算得到一组容积利用系数λe的数据系列1.在Excel软件中，采用“插入→图表→XY散点图→趋势线→多项式→选项→显示公式”的功能，得到的拟合方程为，

(17)

N=3时，容积利用系数的拟合曲线和拟合方程如图6所示.图6曲线显示，拟合精度极高，4阶多项式拟合足能满足要求.

图6拟合曲线和拟合方程

定义，

(18)

式中，v为转子峰顶的切向线速度，一般控制在30～50 m/s之间；n为转速；φL为转子宽径比，一般控制在1～2 之间；Qs为实际抽速；λgas=0.8～0.9为吸气系数，常取λgas=0.85[2,9].

以转子副所占立体空间的体积近似为泵的体积，整理后得，

Vinvolute=(2ra)(2ra+2r)L

(19)

式中，L为转子的宽度.

则，优化模型为，

(20)

式中，OF表示目标函数；DV表示设计变量；CF表示约束函数，其中，r=int()表示r取整数.

当实例参数取，N=3、δ=0.1 mm、λgas=0.85、n=2 000 r/min、Qs=1.5 m3/s时，优化结果为，105 mm的节圆半径和1.367的形状系数.此时，并没有采用N=3下1.464的最大形状系数，说明存在一个优化设计的问题.

8 结 论

本研究认为：峰圆弧与谷圆弧仅为型线的过渡曲线，并不参与啮合运动；经三维模型验证，渐开线型线均能实现单个零件和装配件模型的全参数化；容积利用系数的拟合精度高，且4阶的多项式拟合足能满足设计要求；实例参数下，105 mm节圆半径和1.367形状系数的优化结果，说明转子尺寸存在着一定的优选.

[1]刘坤,李培印,李强，等.三轴罗茨真空泵的抽气理论和结构设计[J].真空科学与技术学报,2015,35(8):934-939.

[2]Garambois P,Donnard G,Rigaud E，et al.Multiphysicscouplingbetweenperiodicgearmeshexcitationandinput/outputfluctuatingtorques:Applicationtoarootsvacuumpump[J].J Sound Vibr,2017,405(1):158-174.

[3]Wang J,Cui D,Pang X,et al.Geometricdesignandperformanceanalysisofanovelsmoothrotorprofileofclawvacuumpumps[J].Vacuum,2017,143(2):174-184.

[4]李海洋,赵玉刚,胡柳,等.渐开线型罗茨真空泵转子型线的改进研究[J].机床与液压,2011,39(22):37-39.

[5]张帅,宋爱平,田德云，等.罗茨泵转子的轮廓型线设计及仿真[J].机械传动,2014,38(3):91-93，101.

[6]杨常青.三级罗茨泵直腰茧形转子型线的研究[J].真空,1986，23(6):8-13.

[7]朱超颖,林景殿,苏中地.一种新罗茨转子型线的构成方法[J].真空科学与技术学报,2015,35(12):1449-1452.

[8]胡祖藩.各种齿型罗茨泵面积利用系数的计算及比较[J].流体工程,1989,18(2):27-35.

[9]李玉龙．UGNX 9.0机械CAX教程[M]．成都：西南交通大学出版社，2015．

[10]Hsieh C F,Deng Y C.Adesignmethodforimprovingtheflowcharacteristicsofamultistagerootspumps[J].Vacuum,2015,121(3):217-222.

ParameterizationandOptimizationResearchonInvoluteProfileofRotor

LIYulong,RANGuangze，ZHANGChenhao

(School of Mechanical Engineering, Chengdu University, Chengdu 610106, China)

In order to achieve the shaped-profiles parameterization and design optimization of involute rotor pairs for roots pump and based on the forming principle of involute,the paper,from five aspects of geometric relationship,theoretical involute shaped-profiles,value range of shape coefficient,practical involute shaped-profiles and parametric model,proposes the full parametric coordinate equation of involute shaped-profiles and its corresponding 3D model construction method.Then by using pitch circle radius and shape coefficient as two design variables,the minimum wrapping cube space volume of rotor pair as an objective function,the optimized model is constructed and a case study is done.All results show that the peak-arc and the valley-arc are only served as transition curve not engaged in the meshing movement;the full parameterization of single part and assembly rotor parts can be realized in corresponding 3D parametric model experiments.The fitting accuracy of the volume utilization coefficient is high,so that the four-order polynomial fitting is needed to meet the design requirements.The optimization results obtained under the condition of the optimal pitch circular radius of 105 mm and the optimal shape coefficient of 1.367 illustrate the necessity of optimization of the rotor size.It is concluded that the full parametric modeling methods and design method can be used for other shape rotor of roots pump.

roots pump;involute rotor;parametric shaped-profiles;volume utilization coefficient;design optimization

TB752+.26；TH166

A

1004-5422(2017)04-0398-04

2017-08-15.

四川省教育厅自然科学基金(16ZA0382)资助项目.

李玉龙(1968 — )，男，博士，教授，从事泵理论与玑代设计方法研究.