基于数据密度感知的非平衡数据模糊聚类方法

王 进，游 磊，黎忠文，苗 放

(1.成都大学 信息科学与工程学院，四川 成都 610106； 2. 成都大学 大数据研究院，四川 成都 610106)

基于数据密度感知的非平衡数据模糊聚类方法

王 进1，游 磊1，黎忠文1，苗 放2

(1.成都大学 信息科学与工程学院，四川 成都 610106； 2. 成都大学 大数据研究院，四川 成都 610106)

非平衡数据分析是数据领域的重要问题之一，其类间分布的巨大差异给聚类方法带来严峻挑战.围绕非平衡数据聚类问题，分析了非平衡数据对模糊聚类方法的影响，提出了基于密度感知的模糊聚类方法.方法将数据分布密度特征嵌入模糊聚类初始化过程中，用于定位初始聚类中心点，避免了少数类中心点位置的消失，在此基础上进一步设计了基于密度的模糊聚类优化更新方法.经数据集分析验证，本研究方法能够有效解决非平衡数据分类中少数类消失问题，并且在聚类算法性能上比传统方法有明显提高.

模糊聚类；分布密度；非平衡数据

0 引 言

模糊聚类方法(fuzzy C-means，FCM)，是一种典型的非监督学习方法，其在传统聚类方法的基础上，模糊聚类方法引入隶属度概念，刻画了每个数据个体与不同类的相似性，隶属度最大的类被视为该数据个体的母类.对数据隶属度分布的分析，可以得到数据个体的细节特征.然而，如何处理非平衡数据聚类依然是模糊聚类面临的一个重要问题[1].非平衡数据的主要特征在于不同类的数据量差异巨大，占多数数据量的主要类往往对聚类结果起决定性影响，造成占少数数据量的次要类在聚类结果中逐渐消失.针对该问题，现有研究主要通过聚类权重进行解决，即按照每类所含数据量分配类权重，确保少数类不受多数类影响，例如，csiFCM、ssFCM、FMLE及siibFCM等[2-6].事实上，由于大多数数据是无标记的，聚类初始无法明确得到每类所含数据点数，使得基于权重的方法应用受到一定的限制.数据分布密度是数据集的重要特征，反映了数据的空间几何结构.在低维场景下，可直接通过数据分布密度获取数据聚类信息，高密度区域通常代表潜在的聚类(见图1).基于该思路，本研究通过数据分布的密度特征进行聚类：聚类初始，通过数据密度选择初始中心点；聚类过程中，采用潜在中心点附近数据点更新聚类中心位置，由此避免少数类消失问题.具体实现时，采用分治思路对模糊聚类算法重新设计，将FCM算法扩展至可并行计算，应用数据分布密度解决非平衡数据聚类问题.

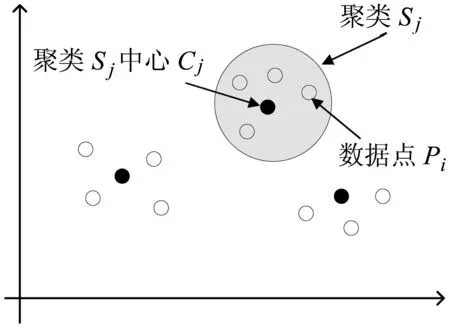
图1聚类分布示意图

1 基于密度的模糊聚类算法设计

基于密度的模糊聚类方法，旨在利用数据集的空间几何结构来优化聚类算法.对此，本研究首先利用高斯核密度估计方法获取数据的分布密度，将数据集粗分为不同子集，针对不同子集进行局部迭代优化，确保少数类中心点不消失.数据集粗分与子集局部优化是该方法需要解决的2个重要问题.

1.1 基于密度的数据划分方法设计

通常，聚类中心点邻域的数据分布密度略高于附近邻居点的邻域密度，且距离更高密度点较远[7].基于该特征，下面给出其具体数学模型，其中包括局部密度和特征距离2个参数.

(1)

其中，‖xi-xj‖为欧式距离，dc为距离门限值.

特征距离δi定义为数据点xi到距离其最近的高密度点的距离，如式(2)所示.

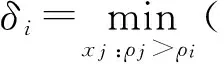
(2)

基于有向无环图的数据集粗分方法如图2所示.其中，端点表示数据点，端点之间的有向边表征其有向邻居关系，有向边的长度则为其特征距离.

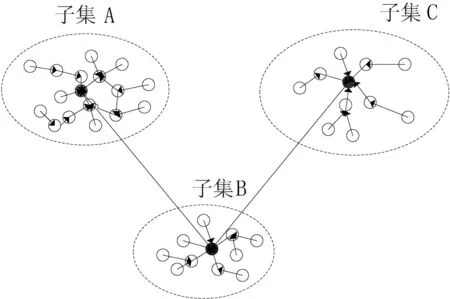
图2基于有向无环图的数据集粗分方法

定义1 数据点p的有向邻居定义为距离该点最近的高密度点，即，

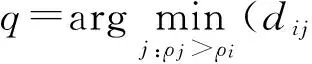
有向邻居点的若干特性如下：

1)全局密度最高的数据点没有有向邻居点，从算法设计角度考虑，将其特征距离设置为，

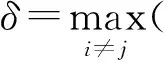
2)有向邻居点之间密度服从，ρpρq；

3)每个数据点有且仅有一个有向邻居点；

4)有向邻居关系是不可逆的，即数据点p的有向邻居为q，但数据点q的有向邻居不是p.

由图2可知，特征距离小的数据点通常跟其有向邻居位于同一个类中，而特征距离较大的点则与其有向邻居位于不同类.由此，将有向邻居图按照有向边长度进行粗分为不同区域，即潜在的类.具体分割方法如下：对于任意数据点，如果其特征距离小于门限dc,则将其划分到与其有向邻居相同的区域；否则，以该点为中心点构建潜在新类.其类归并伪代码如下：

InputtCen={tc1,tc2，…，tck，…，tcM};

Input {tClustk}，k=1,2,…，M;

Input the cluster number C;

tCennew=sortWithGama(tCen,′descending′)

FORj=1:(M-C),

waitForMerge=tCennew[M-j+1];

mergeTo=dirNeighborOf(tCennew[M-j+1]);

tClustmergeTo=Append(tClustwaitForMerge);

END;

由此，将数据集粗分为若干潜在聚类，其中心点具有局部最大的数据密度.本研究将门限dc设置为所有数据距离的2分位点.实际应用中，门限还可以通过优化得到.

依据聚类数量，进一步将上述潜在聚类归并，并优化数据集分割.假定潜在聚类为，

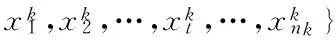
其中，k和nk分别为聚类标识和每个子类tClustk中数据点数量,子类中心点为tCen={tc1,tc2,…，tck，…，tcM}⊂X.

由于潜在聚类中心点通常同时具有较大特征距离和数据密度[7].基于此，本研究依据γi=δi*σi对所有子类中心进行排序，将所有子类归并到就近的c个子类中，完成子类归并.

1.2 子集聚类优化方法

围绕上述得到的子类，{tClustk}，k=1,2,…，C，进一步设计基于密度的聚类优化方法，

FN×C=[f1，1，f1，2，…，f1，C；…；fN，1，fN，2，…，fN，C]

来表示初始划分的聚类关系，其中，

本研究进一步将聚类中心点计算方法设计为如式(3)所示，

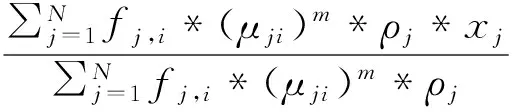
(3)

每次局部中心点位置更新只取决于局部子类中的数据点.模糊聚类的隶属度和目标函数分别为，

(4)

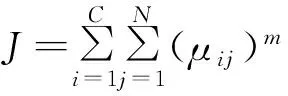
(5)

基于密度的模糊聚类算法伪代码如下：

InputtCen={tc1,tc2,…，tck，…，tcM};

Input {tClustk},k=1,2,…，M;

Input the cluster number C,ε;

[tCennew，tClustnew]=Merger(tCen,tClust);

Computed(xi,vj) with Eq. 4;

Compute membership with Eq. 5.

WHILE|Ji+1-Ji|>ε,

Update centroids with Eq. 3;

Computed(xi,vj) with Eq. 4;

Compute membership with Eq. 5.

END;

2 算法性能评估

本研究采用具有代表性的非平衡数据集ecoli-0-1-4-6[9]评估来研究所提算法的性能.数据集ecoli-0-1-4-6包括阳性和阴性2类数据，其中阳性类数据有20例，阴性类数据有260例，数据维度为8.另一个数据集来自文献[7]，该数据集包括2 535数据样本，共5类，每个数据样本维度是2，其每个类所包含的数据量分别为，C1n=1 456,C2n=246,C3n=246,C4n=431,C5n=156.该数据集是无标记的，并且含有噪声(见图3).同时，本研究应用文献[7]方法对数据进行标记，去除部分噪声.表1详细给出上述2个数据集的特征信息.

表1 数据集描述

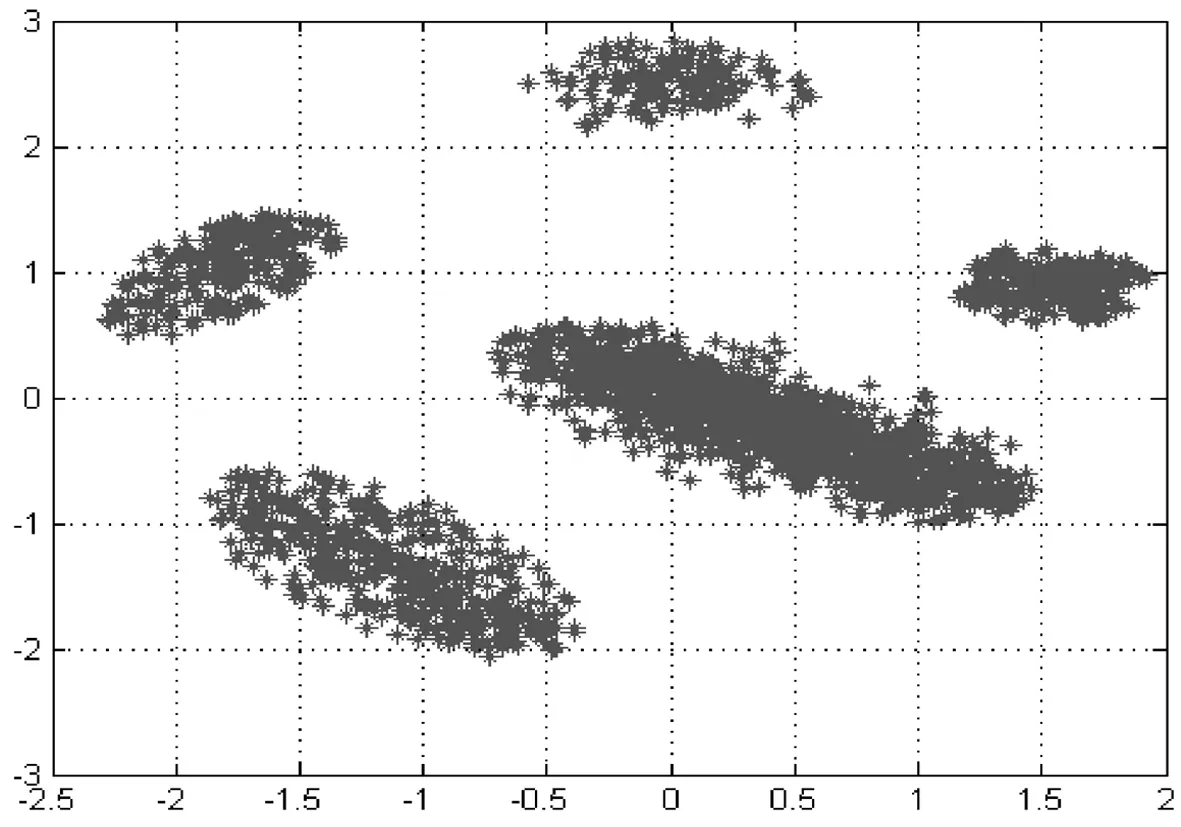
图3文献[7]数据集分布

算法性能的比较主要通过聚类准确性与迭代次数来衡量算法在聚类性能和计算性能的差异.

首先，采用文献[7]数据集分析非平衡数据对聚类性能的影响.该数据集包括2个主要类和3个少数类(见图3)，其中3个少数类分别与2个主要类极为接近，易受到主类影响.图4与图5为采用传统模糊聚类方法得到的聚类结果.

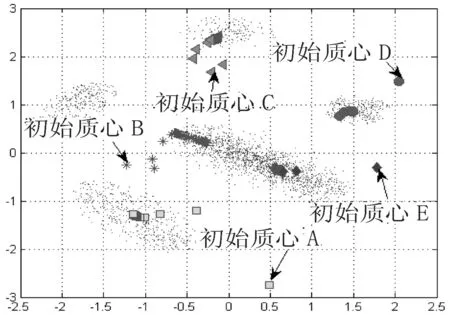
图4传统模糊聚类方法的中心点变化

由图4、图5可知，其中1个多数类被误分为2个类.究其原因，传统聚类算法采用随机选择初始中心点，且通常距离真实聚类中心点距离较远(见图4)，随着聚类优化过程不断进行，聚类中心点逐渐倾向于附近的主要类区域，造成最后没有聚类中心点落在少数类，尤其初始中心点B，最后漂移到附近的多数类区域.可以看出，传统模糊聚类方法在处理非平衡数据问题的误分类率较高.

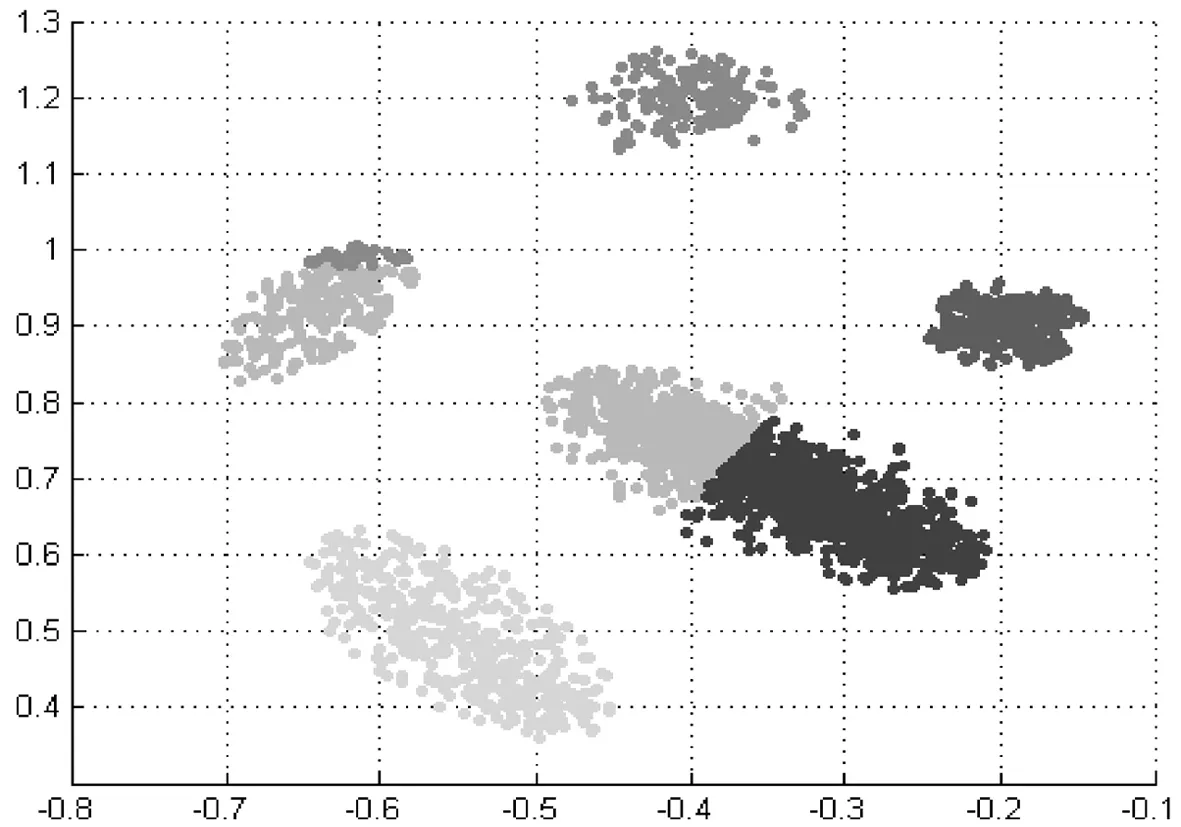
图5传统模糊聚类方法在文献[7]数据集的聚类结果

相比之下，本研究设计的基于密度的聚类方法则始终能保证聚类中心点位于数据分布的高密度区域(见图6、图7). 由于本研究采用局部数据密度来优化模糊聚类，使得聚类中心点能够以较少的迭代次数平稳地收敛.在聚类迭代次数上，本方法仅需要13次聚类迭代，而传统方法则需要30次；在计算时间上，本方法依然比传统方法有优势，具体如表2～表4所示.同时，本研究进一步采用数据集ecoli-0-1-4-6来评估模糊聚类算法和基于密度的模糊聚类算法性能.相比于文献[7]数据集，数据集ecoli-0-1-4-6空间分布相对较散(见图8).数据分布密度差异不明显，可通过此类数据来评估本研究方法在数据空间分布密度差异较小场景下的可用性.由计算结果也可以看出，聚类方法在此类数据集上分类准确性不高.尽管如此，本研究方法依然能够达到比传统方法更优的结果(见表3、表4).

图6基于密度聚类过程的中心点变化

图7本研究方法的聚类结果

表2 聚类计算迭代次数评估

表3 计算时间评估

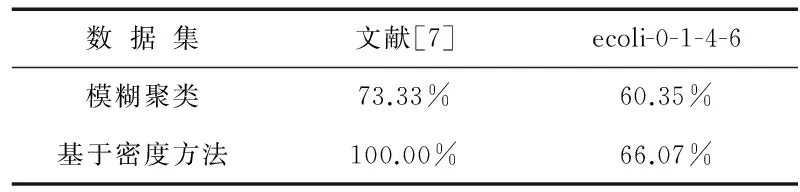
表4 聚类准确性比较

图8数据集ecoli-0-1-4-6的低维分布

3 结 语

针对非平衡数据聚类少数类消失问题，本研究提出并设计了一种新的模糊聚类算法，该方法采用数据分布密度进行聚类初始点选择，旨在解决非平衡数据分布造成聚类准确率低的问题.同时，本研究进一步将密度分布应用于模糊聚类优化过程，提升了聚类算法计算性能.数据集上的测试结果表明，本方法确实能够提升非平衡数据聚类性能，而且能有效降低聚类迭代次数，展示出了处理大数据的潜力.

[1]Clark M C,Hall L O,Goldgof D B，et al.Mrisegmentationusingfuzzyclusteringtechniques[J].IEEE Eng Med Biol,1994，13(5):730-742.

[2]Beyan C,Fisher R.Classifyingimbalanceddatasetsusingsimilaritybasedhierarchicaldecomposition[J].Pattern Recogn，2015，48(5)：1653-1672.

[3]Noordam J C,Van den Broek W H A M，Buydens L M C,et al.Multivariateimagesegmentationwithclustersizeinsensitivefuzzyc-means[J].Chemometr Intell Lab Syst，2002，64(1)：65-78.

[4]Bensaid A M,Hall L O,Bezdek J,et al.Partiallysupervisedclusteringforimagesegmentation[J].Pattern Recogn，1996，29(5)：859-871.

[5]Gath I,Geva A.Unsupervisedoptimalfuzzyclustering[J].IEEE Trans Pattern Anal Mach Intell，1989，11(7)：773-781.

[6]Lin P L,Huang P W，Kuo C H,et al.Asize-insensitiveintegrity-basedfuzzyc-meansmethodfordataclustering[J].Pattern Recogn，2014，47(5)：2042-2056.

[7]Rodriguez A，Laio A.Clusteringbyfastsearchandfindofdensitypeaks[J].Science,2014，344(6191):1492-1496.

ImbalancedFuzzyClusteringMethodBasedonDataDensityPerception

WANGJin1,YOULei1,LIZhongwen1,MIAOFang2

(1.School of Information Science and Engineering, Chengdu University, Chengdu 610106, China; 2.Institute of Big Data, Chengdu University, Chengdu 610106, China)

Imbalanced data analysis is a key part in biomedical areas but poses a computational challenge for clustering methods due to the huge differences in the distribution between categories.This paper discusses the effects of imbalanced datasets on fuzzy clustering method based on imbalanced data clustering,and proposes a data-density-aware fuzzy clustering method to solve this problem.Specifically,a dataset is segmented into different areas with similar local density,and then a novel fuzzy clustering algorithm is implemented based on the initial partition.As a result,the initial clustering center point can be located and the disappearance of the minority class central point can be avoided.An updated method is further optimized based on data-density-aware fuzzy clustering,which is based on the above mentioned initial density method.The experimental results show that our method can better deal with the disappearance of the minority class in imbalanced datasets classification and compared with the traditional FCM,the clustering algorithm performance of the new FCM is obviously enhanced.

FCM;distribution density;imbalanced dataset

TP301.6

A

1004-5422(2017)04-0373-04

2017-08-25.

四川省教育厅自然科学基金(17ZA0082)资助项目.

王 进(1980 — )，男，博士，讲师，从事机器学习相关技术研究.