使用最小串行策略的小通用脉冲神经膜系统

李 立

(安庆广播电视大学，安徽 安庆 246003)

使用最小串行策略的小通用脉冲神经膜系统

李 立

(安庆广播电视大学，安徽 安庆 246003)

膜计算是生物计算的新分支，具有强大的计算能力和潜在的应用价值.使用最小串行策略的脉冲神经膜系统是一类基于神经元细胞的膜计算模型，在该系统中引入带权的突触，分别构造了含有71个神经元的基于最小脉冲数目的函数计算型小通用串行脉冲神经膜系统和含有66个神经元的基于最小脉冲数目的数的产生型小通用串行脉冲神经膜系统，通过模拟注册机证明了2个系统的通用性.

膜计算；脉冲神经膜系统；突触；通用性；注册机

0 引 言

2006年，Ionescu等[1]根据神经网络中神经元相互之间通过突触来处理脉冲的生物现象提出了脉冲神经膜系统.脉冲神经膜系统的拓扑结构可以用有向图来表示，其中的节点表示神经元.神经元之间的脉冲信号由用弧线表示的突触传递，每个神经元中包含若干个脉冲及一定数量的激发规则和遗忘规则.据此，国内外学者根据不同的生物动机提出了一些特殊的脉冲神经膜系统，并对其计算性能进行了研究[2-8].小通用计算设备具有良好的通用性和扩展性，可以节约开发成本，缩短研发周期，因此对小通用计算系统的研究一直是业内的热点[9-10].本研究探讨使用最小串行策略的脉冲神经膜系统的小通用性，并对文献[8]构造的含137个神经元的函数计算型和含126个神经元的数的产生型的基于最小脉冲数目的小通用的串行脉冲神经膜系统进行了改进，引入了带权的突触，将神经元的个数分别降到71和66.

1 相关定义及概念

1.1 基于最小脉冲数目的串行脉冲神经膜系统

标准的脉冲神经膜系统的形式化[1]定义为，

Π=(O,σ1,σ2，…，σm，syn,in,out)

其中：

1)O={a}是系统中脉冲的集合.

2)σ1，σ2，…，σm代表系统中的m(m≥1)个神经元，记为，σ1=(ni，Ri)(1≤i≤m)，其中，ni≥0表示神经元σi中包含的初始脉冲数，Ri是具有下列2种形式的规则构成的有限集合.

激发规则：E/ac→a;d(c≥1,d≥0),E为a的正则表达式，d表示神经元从被激发到发送脉冲所间隔的时间，称为时延.如果神经元σi中含有k个脉冲，满足ak∈L(E)(k≥c),那么神经元σi被激发，消耗c个脉冲，并在d步后向其相关的神经元分别送出1个脉冲.若规则E/ac→a;d满足E=ac，则可以简写成ac→a;d，若同时d=0，则可以直接简写为ac→a.

遗忘规则：as→λ(s≥1),对Ri中的任意规则E/ac→a;d，都满足as∉L(E)；如果神经元σi中包含s个脉冲，则Ri中的遗忘规则as→λ(s≥1)将被使用，其中的全部s个脉冲被消耗掉，且不会产生新的脉冲.

3)syn⊆{1,2,…，m}×{1,2,…，m}表示神经元之间的突触连接，对每个1≤i≤m，都有(i,i)∉syn，若用正整数w表示突触的权值，则带权的突触记为(i,j,w).

4)in,out∈{1,2,…，m}分别表示输入神经元和输出神经元.

对于基于最小脉冲数目的串行脉冲神经膜系统，在每步计算中，若有多个活跃神经元(即满足激发条件的神经元)，则只有脉冲数目最少的活跃神经元可以使用对应规则激发.若同一时刻含最小脉冲数目的活跃神经元有多个，则可以非确定性地选择1个神经元开始激发.

1.2 通用注册机

本研究构造的基于最小脉冲数目的串行脉冲神经膜系统的通用性是通过模拟通用注册机来实现.注册机M=(m,H,l0,lh,I)有3种形式的指令，即：加法指令(li:(ADD(r),lj))，减法指令(li:(SUB(r),lj,lk))和终止指令(lh：HALT).注册机可以在产生模式或接受模式下工作，产生或接受所有的图灵可计算数集.先向注册器r1,r2,…，rk中输入参数n1,n2,…，nk，然后从起始指令l0一直执行到终止指令lh，此时特定的注册器rt中存储的数就是函数计算的结果.

本研究采用文献[9]的1个特定通用注册机Mu=(8,H,l0,lh,I)的指令集，如图1所示.输入的数分别存放在注册器1和2中，计算结果存放在注册器0中.

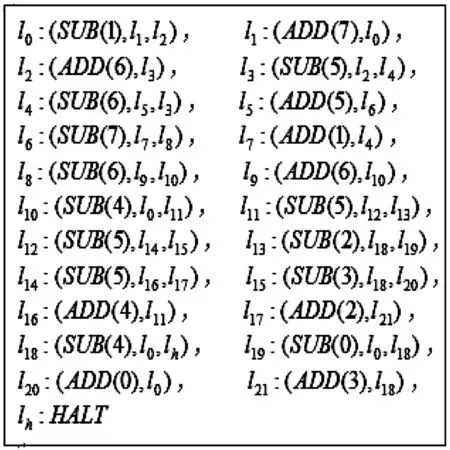
图1文献[9]中的小通用注册机

2 基于最小脉冲数目的函数计算型小通用串行脉冲神经膜系统

定理1 存在1个包含71个神经元的基于最小脉冲数目的函数计算型小通用串行脉冲神经膜系统.

证明从环境中读取二进制字符串102n1102n21…102nk1，其中1对应的每个计算步骤表示输入神经元收到1个脉冲.将计算结果定义为输出神经元发送前2个脉冲的时间间隔，在系统发出第2个脉冲后，计算停止.若系统产生形如0b104r-21(b≥0)的脉冲串，则计算结果为，r=f(n1,n2,…，nk).

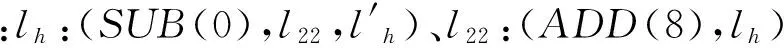
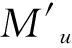
系统Π中的确定型加法模块如图2所示，模拟加法指令li:(ADD(r)，lj).初始时，神经元σr中含有(2n+2)(n≥0)个脉冲，即注册器r中存储的数为n.神经元σli收到1个脉冲后开始激发，使用规则a2/a→a，向神经元σlj和σr各发送1个脉冲.由于突触(li,r,2)的权为2，则神经元σr和神经元σlj分别获得2和1个脉冲.神经元σr中的脉冲数增加了2个，即模拟了注册器r中存储的数加1，而神经元σlj下一步可以激发系统，开始模拟注册机中的lj指令.

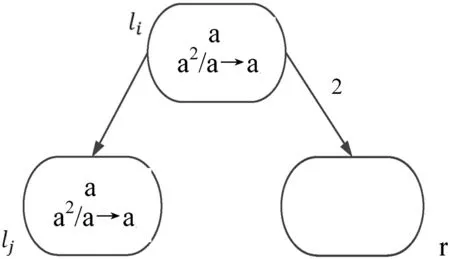
图2系统Π的加法模块

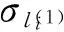
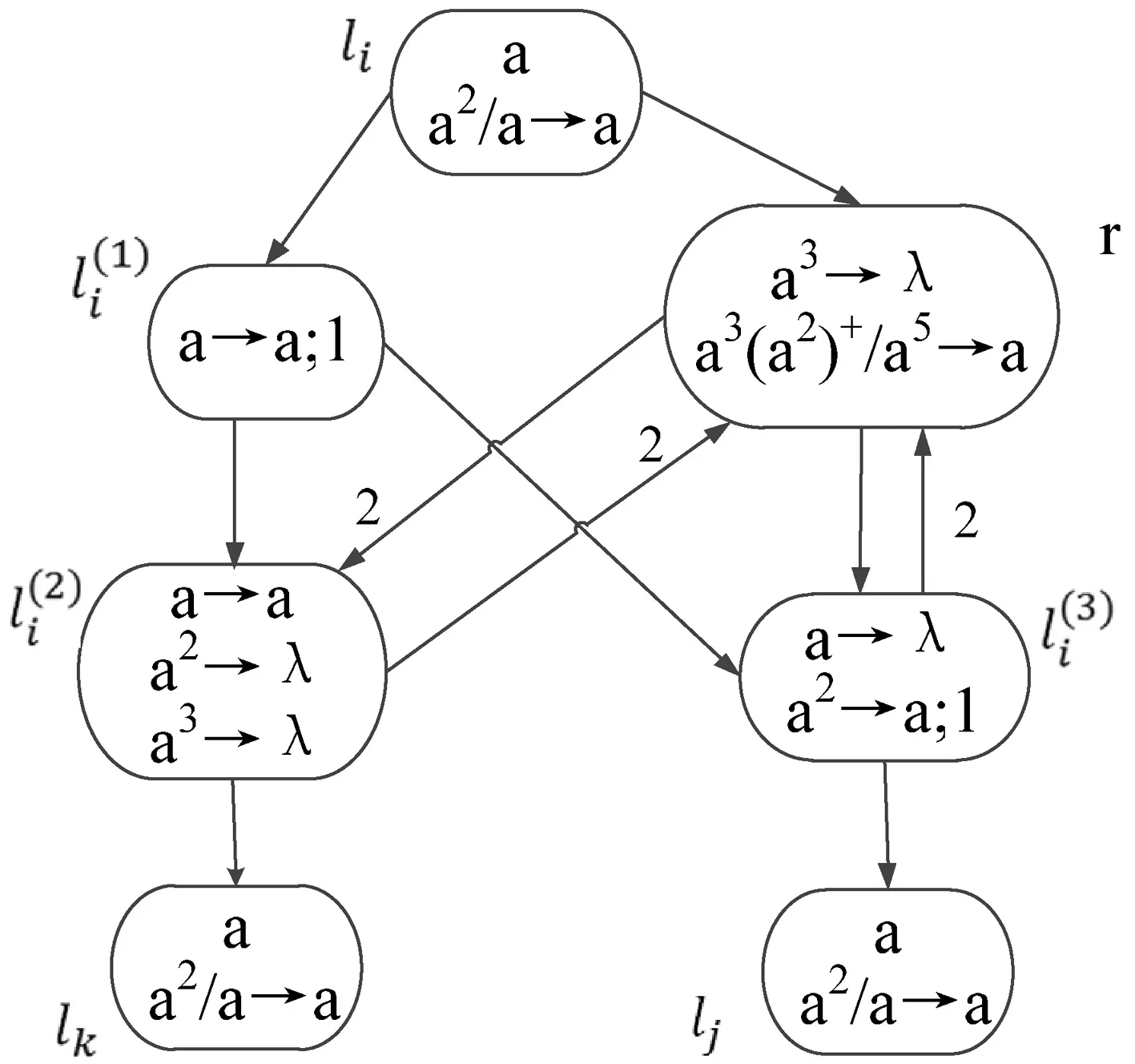
图3系统Π的减法模块

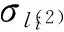
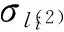
因此，从神经元σli的激发开始，如果注册器r中存储的数大于0，则减去1，系统结束于神经元σlj；如果注册器r中存储的数等于0，系统结束于神经元σlk.系统Π正确地模拟了相对应的减法指令li:(SUB(r),lj,lk).

对某个注册器r来说，可能会存在多个加法指令和减法指令作用在相同的注册器r上，加法模块和减法模块之间可能的相互影响分析如下：

在图2所示的加法模块中，神经元σr每次都是收到2个脉冲，不会激发其中的任何规则，因此在加法模块之间以及加法模块和减法模块之间都没有相互影响.

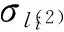
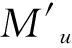
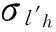
1)若n=1，神经元σ8含有3个脉冲数，将优先激发，向神经元σd1和σout各发送1个脉冲.第t+3步，神经元σ8、σd1和σout的脉冲数分别为1、5、2，只有神经元σout可以激发，向环境发送第2个脉冲，计算停止，此时产生的脉冲串为0b1021.

2)若n≥2，则神经元σd1优先激发，向神经元σout发送1个脉冲，由于突触(d1，out,2)的权为2，神经元σout获得2个脉冲.第t+3步，神经元σout使用其中的遗忘规则a3→λ，移去现有的3个脉冲.第t+4步，神经元σ8激发，之后，神经元σd1、σout、σ8依次激发，不断重复，直到第(t+4n-2)步，只剩余3个脉冲的神经元σ8再次激发，向神经元σd1和σout各发送1个脉冲.第(t+4n-1)步，神经元σ8、σd1和σout的脉冲数分别为1、5、2，只有神经元σout可被激发，向环境送出第2个脉冲，计算停止，产生的脉冲串为0b104n-21.

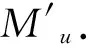
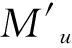
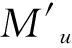
2)分析6组顺序执行的减法指令和加法指令(l0和l1、l4和l5、l6和l7、l8和l9、l14和l16、lh和l22)可知：对应的中间指令(l1,l5，l7，l9，l16，l22)在模拟的小通用注册机的其他指令中都未出现，可以把每组的减法指令和加法指令合并，每组可节省2个神经元，6组可减少12个神经元.

故，系统共需要使用71个神经元.

定理1得证.

3 基于最小脉冲数目的数的产生型小通用串行脉冲神经膜系统

定理2 存在1个包含66个神经元的基于最小脉冲数目的数的产生型小通用串行脉冲神经膜系统.

证明作为产生数集的装置，脉冲神经膜系统的通用性定义[10]为，设(φ0，φ1，…)为一元部分递归函数的1个固定可枚举，对于数的产生型脉冲神经膜系统，存在1个递归函数g，对所有自然数x，若向系统输入数g(x)，系统产生的数集为{n∈N|φX(n)}，则称其是通用的.

对第2节构造的系统做3点修改，就可以得到相应的基于最小脉冲数目的数的产生型小通用串行脉冲神经膜系统Πu.

1)系统Πu不需要单独的输出模块用来输出计算停止后的结果，因此指令lh和注册器8可省略，把输入模块和输出模块合并为1个.通过从环境读取符号串102g(x)1，向神经元σ1中存入2g(x)个脉冲.

2)合并后的输入—输出模块在计算开始时随机产生1个自然数n，即向神经元σ2中存入2n个脉冲，同时输出形如104n-21的脉冲串.

3)为了检测部分递归函数φx是否对n已定义，开始执行如图1所示的注册机Mu，其中的注册器1和2中已分别存入数g(x)和数n.若注册机Mu中的计算停止，即构造的系统Πu停机，则系统Πu产生了数n.

由此得到系统Πu中含有神经元的个数统计为，8+22+13*3+8=77.根据上述优化方法，系统Πu中的1组顺序执行的加法指令和5组顺序执行的减法指令和加法指令，可以减少11个神经元.

故，系统Πu一共需要使用66个神经元.

定理2得证.

4 结 语

本研究研究了基于最小脉冲数目的串行脉冲神经膜系统的小通用性.作为计算函数的装置，本研究构造了1个含有71个神经元的基于最小脉冲数目的小通用串行脉冲神经膜系统；作为产生数集的装置，本研究构造了1个含有66个神经元的基于最小脉冲数目的小通用串行脉冲神经膜系统.带权突触的引入减少了辅助神经元，使得构造的2个小通用系统比文献[8]中的系统使用的神经元数目减少了近一半.下一步的研究计划能引入更新的思路和更好的证明技巧，构造出所需神经元更少的基于最小脉冲数目的小通用串行脉冲神经膜系统.

[1]Ionescu M,Pǎun G，Yokomori T.SpikingneuralPsystems[J].Fundam Inform,2006,71(2):279-308.

[2]Pǎun G.AquickoverviewofmembranecomputingwithsomedetailsaboutspikingneuralPsystems[J].Front Comput Sci Chin,2007,1(1):37-49.

[3]Metta V P,Krithivasan K.ParallelprogramminginspikingneuralPsystemswithanti-spikes[J].Sci Technol,2014,17(1):33-45.

[4]Paun G.SpikingneuralPsystemswithastrocyte-likecontrol[J].J UCS,2007,13(11):1707-1721.

[5]Pan L,Wang J,Hoogeboom H J.SpikingneuralPsystemswithastrocytes[J].Neural Comput,2012,24(3):805-825.

[6]Song T,Pan L,Paun G.SpikingneuralPsystemswithrulesonsynapses[J].Theoret Comput Sci,2014,25(9):82-95.

[7]Pǎun A,Sidoroff M.SequentialityinducedbyspikenumberinSNPsystems:Smalluniversalmachines[J].Lect Notes Comput Sci,2011,71(84):333-345.

[8]Jiang K Q,Huang Y F,Xu J B.SmalluniversalsequentialspikingneuralPsystemsbasedonminimumspikenumber[J].Rom J Inform Sci Technol,2014,17(1):5-18.

[9]Korec I.Smalluniversalregistermachines[J].Theoret Comput Sci,1996,168(2):267-301.

[10]Pǎun A,Pǎun A G.SmalluniversalspikingneuralPsystems[J].BioSystems,2007,90(1):48-60.

SmallUniversalSpikingNeuralPSystemsWorkinginSequentialModeInducedbyMinimumSpikeNumber

LILi

(Anqing Radio and Television University, Anqing 246003, China)

Membrane computing is a new branch of biological computing with strong computing power and potential application value.Spiking neural P system working in sequential mode induced by minimum spike number is a kind of neural-like computation models in the framework of P systems.In this system,the synapse with weights is introduced.As devices for computing functions,we construct a universal sequential spiking neural P system based on the minimum spike number which uses 71 neurons;as a generator of sets of numbers,a universal sequential spiking neural P system based on minimum spike number with 66 neurons is also obtained.The universality of the two systems is demonstrated by simulation registers.

membrane computing;spiking neural P system;synapse;universality;register

TP301

A

1004-5422(2017)04-0385-05

2017-10-11.

安徽省教育厅高校自然科学基金(KJ2017A942)资助项目.

李 立(1980 — )，女，硕士，副教授，从事膜计算与数据挖掘研究.