稳流仓料位的T-S模糊建模

谢娅妮，袁铸钢，张 强

(济南大学 自动化与电气工程学院，山东 济南 250022)

稳流仓料位的T-S模糊建模

谢娅妮，袁铸钢，张 强

(济南大学 自动化与电气工程学院，山东 济南 250022)

为利用基于模型的方法研究稳流仓的料位控制问题，提出了一种稳流仓料位的T-S模糊建模方法。基于水泥联合粉磨工艺分析，结合现场采集的数据，采用回归分析和最小二乘支持向量机(LS_SVM)的学习算法建立了稳流仓料位不同工况下的数学模型；结合稳流仓料位工作特点划分隶属度曲线，建立其T-S模糊模型；仿真结果表明所提方法的有效性。

稳流仓料位；回归分析；最小二乘支持向量机；T-S模糊模型

稳流仓是水泥联合粉磨预粉磨环节重要的一部分，其料位的高低是影响预粉磨环节辊压机工作效率高低的关键[1]。稳流仓对物料进行缓冲，是保证物料进入辊压机之前能够充分混合的设备。由于其自身工况波动频繁，难以精确分析，所以建立一个能够准确反映稳流仓料位变化动态的数学模型对实现稳流仓料位的控制至关重要。

近年来，学者们对水泥粉磨做出了很多研究。文献[2]通过神经网络能任意逼近非线性关系能力的特点，建立了基于神经网络的水泥强度模型；文献[3]根据极限学习机神经网络(ELMNN)建立在线的联合粉磨稳流仓的内部模型；文献[4]介绍了最小二乘支持向量机的基本理论、核函数的选择、模型参数的选取，建立了最小二乘支持向量机水泥比表面积软测量模型。文献[5]在对水泥联合粉磨进行工艺分析的基础上，结合现场数据及经验，对水泥联合粉磨建立了加权最小二乘模型。然而上述文献存在以下问题：文献[2]由于神经网络存在过拟合、局部最小值问题，所以很难达到良好的建模效果；文献[3-5]由于稳流仓料位存在多工况的情况，具有滞后以及非线性等特点，难以建立全局模型，未对稳流仓料位划分工况，在不同的工况下建模分析。因此，它们难以满足工程需求。所以，对稳流仓料位在不同的工况下建立模型是必要的。

图1 半终粉磨工艺图

基于以上分析，本文提出了一种稳流仓料位的T-S建模方法。并通过仿真验证所建模型的准确性和有效性。

1 水泥联合粉磨工艺分析

半终粉磨工艺如图1所示。

图1中，熟料、矿渣、柠檬酸渣等原材料按照一定配比混合的物料经皮带机进入稳流仓，缓冲后稳定地进入辊压机进行辊压，大颗粒的物料被破碎，然后再由入磨提升机进入V选，粗略选粉后较粗的物料重新进入稳流仓进行循环。V选出的略细物料进入前选粉机继续分选，分选后更细的物料在循环风机的带动下进入混料机，前选粉后的粗物料进入球磨机进行粉磨。经球磨机粉磨后的物料，一部分经收尘器直接进入混料机，另一部分在出磨提升机的带动下进入后选粉机进行分选，较粗的物料进入球磨机继续进行研磨，较细的物料经收尘器进入混料机。进入混料机的物料与矿粉混合后进入水泥库。

根据图1工艺流程，假设球磨机终粉磨环节保持恒定，由于辊压机功率一般情况下是固定的，压力也是固定的，可假设稳流仓出口端固定，辊压机电流、入磨提升机电流固定，故稳流仓料位只考虑入口端变量。根据现场工艺和操作员经验，可假设V选粉机转速是固定不变的，那么影响稳流仓料位的因素就是喂料量、前选粉机转速和循环风机转速。

2 稳流仓料位T-S模糊建模

为建立稳流仓料位的数学模型，需要先进行数据预处理。常用的方法有很多，如插值法、中值法、均值法等。本文采用滚动滤波法进行数据预处理，其滤波函数如下：

(1)

式中：xi为第i个经过滤波后的值，xj为采集到的实时数据。本文中n=5，即每次选取5个数据的平均值。

根据工艺分析及现场采集的数据，得到稳流仓料位的工况模板如表1所示。

根据表1中的数据，采用回归分析和最小二乘支持向量机(LS_SVM)的学习算法建立稳流仓料位不同工况下的数学模型，并根据稳流仓料位工况模板划分隶属度曲线，建立稳流仓料位的T-S模糊模型。

表1 稳流仓料位的工况模板

2.1 两种数学模型介绍

本文主要用到多元线性回归分析[6]和最小二乘支持向量机(LS_SVM)[7,8]进行建模。

2.1.1 多元线性回归建模

假设系统为双输入单输出系统，对输入输出得到n组数据，其结构形式：

(2)

其中：y是输出变量；u是输入变量；m、n、p是维数；ε是未知的干扰量；a0、ai、bi、ci是待拟合的参数；i=1,2,…,m,j=1,2,…,n。

为便于分析，将式(2)改写为

y=Φθ+ε。

(3)

利用最小二乘估计，根据式(2)，回归方程可写成:

参数估计向量:

(5)

2.1.2 最小二乘支持向量机建模

假设系统为单输入单输出系统，对于采集的样本数据(x1,y1),…,(xn,yn)其中xk∈RN,yk∈R,k=1,2,...n。在ω空间函数的估计问题为

(6)

(7)

其中：b为偏差量，c为正规化参数，ek为误差变量，k为样本数据个数。

定义拉格朗日函数

(8)

其中：αk是拉格朗日乘子。

核函数定义为

ψ(xk,xl)=φ(xk)φ(xl)。

(9)

其中：k,l=1,2,3…,N。ψ(xk,xl)函数任意对称并满足Mercer条件，式(9)可转化成式(11)的形式：

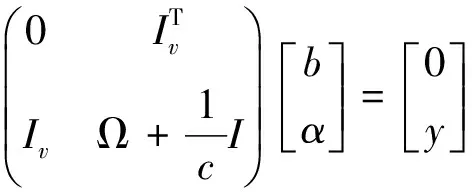
(10)

其中：y=[y1,…,yN]；Iv=[1,…,1]；∂=[∂1,…,∂N]； Ωkl=φ(xk)Tφ(xl)k,l=1,2,3,…,N。

运用径向基函数RBF为通用核函数，即核函数

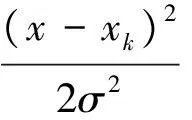
(11)

其中：σ2为核宽。所以LS_SVM模型的函数估计为:

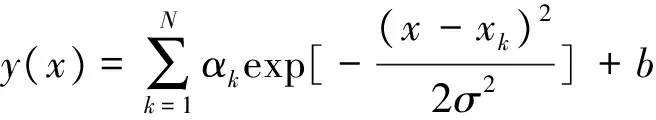
(12)

2.2 稳流仓料位工况1的数学模型

基于以上两种模型，下面将对不同的工况采用合适的模型进行建模。对于工况1，由于其占全工况区段小，但稳流仓料位各参变量波动很大，采用最小二乘支持向量机的学习算法进行建模。

由公式(12)选择喂料量、前选粉机转速、循环风机转速作为输入量，稳流仓料位作为输出量。选择100组训练样本，根据实际应用比较以及经验选取c、σ，其中c=15、σ2=0.5，模型系数α1=-1.168 9,α2=1.522 4,α3=-0.100 5,…,α100=0.820 7,b=-0.002 3。

LS_SVM模型的训练曲线和误差曲线如图2和图3所示。

2.3 稳流仓料位工况2的数学模型

对于工况2，虽然稳流仓料位各参变量呈现非线性变化趋势，但是占据总区间很小，所以采用回归分析的学习算法建立数学模型。

由公式(4)选择100组训练样本，输入喂煤量、前选粉机转速及循环风机转速，输出为稳流仓料位。回归方程可写成：

其中:y1,y2,…,yn是k时刻稳流仓料位的采样值；y1(k-i),y2(k-i),…,yn(k-i)是k-i(i=1,2)时刻的采样值；u1(k-i),u2(k-i),…,un(k-i)值是k-i,(i=1,2,3)时刻喂料量的采样输入值z1(k-i)；z2(k-i),…,zn(k-i)是k-i,(i=1,2,3)时刻前选粉机转速的采样输入值；w1(k-i),w2(k-i)…,wn(k-i)是k-i,(i=1,2,3)时刻循环风机转机转速的采样输入值；ε1,ε2,…,εn是未知的干扰量；ai,bi,ci,di,i=1,2,3是待拟合的参数。

所得到典型工况2的稳流仓料位多入单出模型

工况2的模型训练曲线和误差曲线如图4和图5所示。

2.4 稳流仓料位工况3的数学模型

对于工况3，稳流仓料位各参量波动范围不大，可以采用回归分析的算法建立多输入和单输出的动态模型。方法同上，在此不再赘述。

得到典型工况3的稳流仓料位多入单出模型

典型工况3的模型训练曲线和误差曲线如图6和图7所示。

由图2和图3可以看出，模型拟合值和实际值之间的拟合精度很高。因此，所建的模型一定程度上能够反映稳流仓位变化状态，具有一定的可靠性。由图4～图7可知，所建的模型拟合性能较好，拟合值和实际值之间的误差在范围，符合实际生产要求。

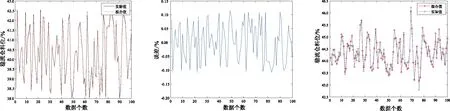
图2 模型训练曲线 图3 误差曲线 图4 模型训练曲线

图5 误差曲线 图6 模型训练曲线 图7 误差曲线

2.5 稳流仓料位工况4的数学模型

对于工况4，此段数据变化不大，但由于此段总空间比较大，暂无法确定采用线性还是非线性的方式进行拟合。假设在此采用近似线性关系进行拟合，采用回归分析的方法，方法同上，在此不再赘述。模型的训练曲线和误差曲线如图8和图9所示。为了得到更精确的模型，对典型工况4采用LS_SVM建立模型。采用公式 (12)选择 100 组训练样本，根据实际应用比较以及经验选取c、σ，其中c=20、σ2=0.5，模型系数α1=-0.989 5,α2=-1.576 0,α3=1.015 3…,α100=1.259 1,b=0.019 6。模型的训练曲线和误差曲线如图10和图11所示。

图8 模型训练曲线 图9 误差曲线

图10 模型训练曲线 图11 误差曲线

由图8和图9所知，训练误差比较大，精确度比较低，不符合实际现场生产需求。由图10和图11可知，误差变化特别小。因此，所建的LS_SVM模型符合实际生产的要求，一定程度上能够反映稳流仓位变化状态，具有一定的可靠性。

2.6 T-S模糊数学模型

模糊隶属函数如图12所示。

μi(u1)的具体形式如下：

(16)

由模型后件结构，得知用模糊规则描述系统的稳流仓料位T-S模糊模型[9,10]可用如下表示：

图12 隶属函数图

R1:Ifu1isA1theny=y1；R2：Ifu2isA2theny=y2；R3：Ifu3isA3theny=y3；R4：Ifu4isA4theny=y4其中：R1～R4为模糊规则；A1～A4为模糊集,A1为u1<42.58,A2为42.58≤u1<48.79,A3为46.38≤u1<48.79,A4为u1≥48.79；y1～y4为上文建立的稳流仓料位局部模型。因此，T-S模型的最终输出可以写成各个子系统输出的加权的形式：

(17)

3 仿真分析

依据上文所述建模方法和模糊建模规则，建立稳流仓料位T-S模糊模型。选取覆盖全工况的100组数据，对比实际的稳流仓料位，验证模型的可靠性。

稳流仓料位T-S模糊模型的仿真验证曲线及误差曲线如图13和图14所示。

由图13和图14可知，模型的误差在±0.5%以内。因此，仿真结果表明该建模方法是有效的，所建立的模型能够描述工况参数的变化，准确地反映了实际输出的被控变量的变化动态。

图13 仿真验证曲线 图14 误差曲线

4 结 语

本文提出了在不同工况模板下利用数据预处理、回归分析和LS_SVM相结合建立稳流仓料位模型。通过不同工况的模型可知，工况2和工况3采用回归分析建模误差较小；工况1和工况4采用回归分析建模误差较大，其采用LS_SVM建模型误差较小。最后结合水泥预粉磨环节稳流仓料位工作特点划分隶属度曲线，建立稳流仓料位T-S数学模型。通过仿真验证可知，模型有效，可用于实际生产现场。

[1] 刘志鹏，颜文俊.预粉磨系统的智能建模与复合控制[J].浙江大学学报(工学版),2012,46(08)：1506-1511.

[2] 郭一军.基于人工神经网络的水泥强度预测模型研究[D].昆明：昆明理工大学,2006：6-10.

[3] 吴茂胜,袁铸钢,张强,等.联合粉磨稳流仓ELMNN建模及其内模控制[J].洛阳理工学院学报(自然科学版),2016,26(1):55-60.

[4] 栾维磊,孟庆金,申涛.基于最小二乘支持向量机的水泥粒度软测量[J].济南大学学报(自然科学版),2013,27(4):347-351.

[5] 任万杰.水泥粉磨系统的建模与控制方法研究[D].济南：济南大学，2013：17-29.

[6] 张承慧，李希霖.最小二乘法在水泥配料成分估计中的应用[J].山东工业大学学报,1989,19(3):9-17.

[7] 顾燕萍,赵文杰,吴占松.基于最小二乘支持向量机的电站锅炉燃烧优化[J].中国电机工程学报,2010,30(17):91-97.

[8] Ehsan S,Jafar A,Mohammad H A.Assessment of Cu(II) adsorption from water on modified membrane adsorbents using LS_SVM intelligent approach[J].Journal of Saudi Chemical Society,2016,20:213-219.

[9] 袁平,王福利.一种T-S模糊系统建模方法[J].系统仿真学报,2006,18(4):817-820.

[10] 郎月.T-S模糊模型的建模研究[D].锦州：渤海大学,2014:4-30.

Weighing Bin of the Combined Grinding Model Via ELMNN and Internal Model Control

XIE Yani,YUAN Zhugang,ZHANG Qiang

(University of Jinan,Jinan 250022,China)

The paper proposes a T-S fuzzy modeling method for weighing warehouse material level. The approach is based on the analysis of the combined cement grinding process and the collected data from the field. A mathematical model,which is for different conditions of the weighing warehouse material level,is established by using regression analysis and the learning algorithm of least squares support vector machine (LS-SVM);Then,on this basis,combined with the working characteristics of Warehouse Material Level,the membership curve is divided and the T-S fuzzy model is established. Finally,the simulation results show the effectiveness of the proposed method.

weighing warehouse material level;regression analysis;Least square support vector machine (LS_SVM);T-S fuzzy model

10.3969/i.issn.1674-5403.2017.03.015

TP273

A

1674-5403(2017)03-0056-06

2016-12-25

谢娅妮(1988-)，女，山东烟台人，在读硕士研究生，主要从事流程工业自动化方面的研究.

山东省科技重大专项项目(2015ZDXX0101F01).