浅谈绝对值函数在高考中的几种考查

☉江苏省宿迁市文昌高级中学 王少鹏

浅谈绝对值函数在高考中的几种考查

☉江苏省宿迁市文昌高级中学 王少鹏

近几年，含有绝对值不等式问题的高考题经常出现，这些试题新颖别致，灵活多变，综合性强，难度大，得分很低.笔者以绝对值函数常考的几种题型来谈谈此类问题的解法.

考查一——两个绝对值相加的函数最值的求法

例1求函数f（x）=|ax-b|+|cx-d|（a＞0，c＞0）的最小值.

图1

图2

图3

图4

图5

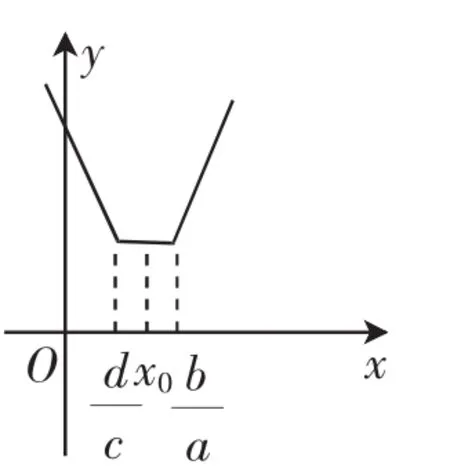
图6

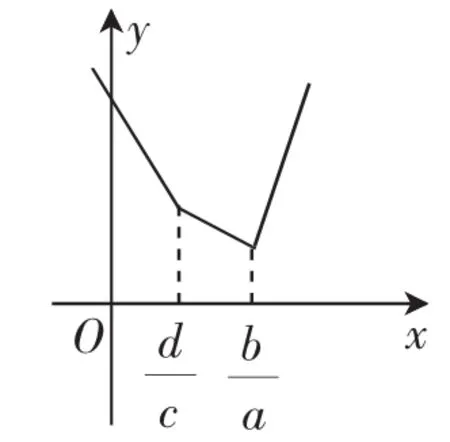
图7

小结：由（1），（2），（3）可知：

也就是说，当正数a和c不相等时，求f（x）min，只需比较正数a和c的大小，哪个大，最小值点就为其所属绝对值里面函数的零点.

考查二——多个绝对值相加的函数最值求法

我们熟悉函数（fx）=|x-a|+|x-b（|a＜b）的性质，其解法可以用函数性质解答，也可以用绝对值求解.事实上，我们很容易想到：若是n个绝对值相加会是什么情况呢？这类问题其实有章可循，可以利用图像特征求解最小值.进一步，再思考：当x的系数不全为1时，其最值又如何求解？下面就借助函数（fx）=作进一步的探讨.

例2若不等式恒成立，求实数m的取值范围.

解析：不等式可化为|2x|+|x-2|+|2（x-1）|＞2m，即|x|+|x|+|x-1|+|x-1|+|x-2|＞2m恒成立.

又函数y=|x|+|x|+|x-1|+|x-1|+|x-2|的最小值为f（1）=3，于是只需3＞2m，得

例3求函数y=|2x-1|+|x-1|+|x-2|的最小值，并求相应x的值.

解析

考查三——含有一个绝对值的函数最值的求法

学生对含参带绝对值的函数的题型都有畏惧心理，这种题型综合性强，学生对其分类讨论的思想辨别不清，对其所需要的分类讨论能力还不够.这类问题，可以充分利用绝对值不等式的性质：||x|-|y||≤|x±y|≤|x|+|y|，其中等号成立的条件满足

笔者通过自己的教学实践，谈谈这类题型的解法.

（1）略；

（3）若对任意实数a，b，总存在实数x0∈［0，4］使得不等式（fx0）≥m成立，求实数m的取值范围.

解析：本题出现，本质上还是二次函数，我们只需换元：令则（fx）=h（t）=|at2-t+b|.

（3）原题等价于对任意实数a，b，总存在实数t0∈［0，2］使得不等式h（t0）≥m成立.先让a，b固定，记M（a，b）是h（t）在［0，2］上的最大值，于是只需M（a，b）≥m，∀a，b∈R，而这又等价于当a，b变化时，M（a，b）min≥m.由（2）可知，，接下来，我们来求M（a，b）min.

本题解法没有完全从函数角度讨论，而是结合绝对值不等式的性质解决.

美国著名数学教育家波利亚曾说：“一个专心的认真备课的老师能够拿出一个有意义的但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就像通过一道门户，把学生引入一个完整的理论领域.”在高中数学教学中，作为一线教师，应多研究解题，多角度考虑，开阔学生视野，发散学生思维，优化学生解题方法.长期以往，我们就能收到意想不到的效果.