失谐叶盘受迫响应的灵敏度分析方法

谭元球，臧朝平,，周标，段勇亮，E.P.PETROV

1.南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，南京 210016 2.赛克斯大学 工程与信息学院，布莱顿 BN1 9QT,英国

失谐叶盘受迫响应的灵敏度分析方法

谭元球1，臧朝平1,*，周标1，段勇亮1，E.P.PETROV2

1.南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，南京 210016 2.赛克斯大学 工程与信息学院，布莱顿 BN1 9QT,英国

针对失谐叶盘结构的受迫响应与叶片失谐之间的敏感性问题，提出了一种失谐叶盘最大响应幅值分别关于叶片频率失谐参数和叶片节点失谐质量的一阶和二阶灵敏度系数计算方法，以探究叶盘结构失谐参数对其最大响应幅值的影响。该方法立足于高保真失谐叶盘减缩建模和响应分析技术，直接对失谐叶盘结构的动力学方程进行推导获取其一阶和二阶灵敏度系数的数学表达式，未引入任何其他近似和简化计算措施，可以有效地求解高保真失谐叶盘最大响应幅值在不同激励频段、激励阶次和失谐形式下的灵敏度系数。该灵敏度分析方法在大规模高保真失谐叶盘结构模型上验证了其有效性。结果表明，与常规的数值差分灵敏度近似计算方法相比，本文提出的灵敏度分析方法在计算精度和计算效率方面具有巨大的优势，对进一步的失谐叶盘响应分析具有广泛的应用前景和通用性。

失谐；叶盘；高保真；灵敏度分析；数学表达式

由于受到叶片加工误差、运行磨损、安装间隙、几何偏差和材料性质差异等不确定因素的影响，实际叶盘结构各扇区之间的物理参数或几何参数不可避免地存在偏差而引入了叶片失谐。叶盘系统对叶片失谐非常敏感，极小的失谐量仍使得振型及激励在叶盘结构中不能均匀地传播，能量集中在较少的叶片上而出现振动局部化现象，从而导致叶片过早地发生高周疲劳失效[1-5]。李其汉等[6]研究表明叶盘结构中由于叶片高阶共振所致的高周疲劳失效是制约航空发动机结构完整性和可靠性的主要问题。因此对失谐叶盘结构在高频范围内的振动特性研究极其重要。

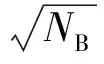
灵敏度系数是目标函数随指定变量变化的梯度信息的定量描述。灵敏度分析在一般结构动力学系统中得到了广泛应用，如Haug[8]，Haftka[9-10]和Komkov[11]等分别开展了线性和非线性动力学系统响应幅值关于设计参数的一、二阶灵敏度系数计算方法的研究；Wang[12]和Oguamanam[13]等分别给出了特征值和频率关于附属刚度和质量的灵敏度计算方法。失谐叶盘结构的最大响应幅值与各个叶片的随机参数差异相关，是典型的高维变量函数。同时，叶片失谐破坏了叶盘结构的循环对称特性，导致其响应特性十分复杂。因此，目前针对失谐叶盘结构开展的灵敏度分析研究相对较少，仅有Petrov等[14-15]在早期研究中分别针对线性系统和非线性简单系统探索研究了叶盘最大响应幅值关于叶片失谐参数的灵敏度计算方法，但没有明确给出一阶和二阶灵敏度系数的计算表达式。

综上所述，本文提出了一种失谐叶盘最大响应幅值分别关于叶片频率失谐参数和叶片节点失谐质量的灵敏度系数计算方法，旨在对大规模高保真叶盘结构有限元模型在高中低阶频率范围进行有效的灵敏度分析，探究叶盘结构各叶片频率失谐参数和各节点失谐质量变化对最大响应幅值带来的影响。该方法立足于本课题组在前期研究中发展建立的高保真失谐叶盘减缩建模和响应分析技术[16-17]，直接对失谐叶盘结构的动力学方程推导获取其一阶和二阶灵敏度系数的数学表达式，未引入任何其他近似和简化计算措施，具有准确、高效的特点，有望在为进一步深入研究失谐叶盘最大受迫响应幅值特性发挥巨大作用。

1 失谐叶盘受迫响应计算

1.1 失谐叶盘复响应

失谐叶盘结构在阶次激励(Engine Order excitation, EO)下的运动方程表示为

(1)

f=[fS, eiα kfS,…,eiα k(NB-1)fS]T

(2)

(3)

式中：c为线性组合系数向量。基于谐调模态及组合系数矩阵表示的失谐叶盘的特征方程为

(4)

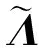
(5)

1.2 节点最大响应幅值

(6)

式中：上标“H”表示对向量取共轭转置。搜寻叶盘所有节点，且选取节点在一个振动周期内的最大位移和工作频率范围内响应最大的激励频率点，即可获得叶盘结构节点最大振动幅值为

(7)

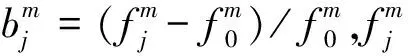
2 灵敏度系数分析方法

2.1 节点响应幅值关于失谐参数的灵敏度

本文仅讨论叶盘失谐是由失谐质量矩阵δM引入的情况，即刚度失谐矩阵和阻尼失谐矩阵假设为零，即式(1)中δD=0和δK=0。失谐叶盘复数响应幅值关于失谐参数的一阶和二阶灵敏度系数可以通对式(1)分别求其前两阶导数获得：

x′=A(ω2δM′x)

(8)

(9)

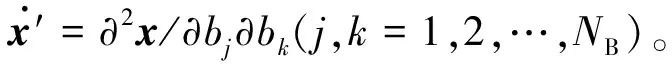
为了获取节点最大位移幅值的灵敏度系数，先对式(6)求关于节点位移向量a的导数，即

(10)

节点最大响应幅值关于叶片频率失谐参数bj的一阶灵敏度系数可表示为

(11)

(12)

其中:wα(α=1,2,…,6)为向量w的第α个元素。将式(12)再一次关于叶片频率失谐参数bk进行求导得

(13)

(14)

(15)

其中:δα β(α,β=x,y,z)为Kronecher符号。

然而，当应用式(11)和式(13)求解节点最大响应幅值的一阶和二阶灵敏度系数时，还需要用到对应节点3个自由度复数响应幅值向量关于叶片频率失谐参数的一、二阶灵敏度系数，即∂w/∂bj和∂2w/∂bj∂bk。因此，在2.2节中，将针对失谐叶盘最大响应幅值关于频率失谐参数和节点失谐质量的灵敏度系数，分别给出节点复数响应幅值向量关于对应失谐参数的灵敏度系数计算方法。此外，两类灵敏度分析中，均假设失谐是由叶盘结构的质量失谐矩阵δM引入，且

δM=diag(δM1, δM2,…,δMNB)

(16)

式中:δMj(j=1,2,…,NB)为第j个扇区的质量失谐矩阵。对于失谐矩阵的构成，首先构建一个常量摄动质量矩阵δMS，使该矩阵为一个集中质量矩阵且其维度与单个扇区自由度数一致，即表示为

δMS=diag(δm1,δm2,δm3,…,δmN)

(17)

其中:δmj(j=1,2,…,N)为施加到扇区第j个自由度的质量元素，一般仅选取叶片表面部分节点失谐质量不为零，其余大部分都为零元素。所以第j个扇区施加的失谐质量矩阵δMj可以表示成常量摄动矩阵δMS与一个失谐水平系数μj相乘，即

δMj=μjδMS

(18)

对于单个叶片，在给定的初始常量摄动矩阵δMS下，叶片的失谐水平系数μj与频率失谐参数bj之间存在一定的函数对应关系μj=μ(bj)。这种对应关系可以通过对叶片设定不同的失谐水平系数进行有限元仿真计算获取[19]，即建立μj与bj之间的对应关系(如图1所示)。

图1 叶片失谐水平系数与频率失谐量的关系
Fig.1 Relationship between mistuning coefficient and frequency mistuning of a single blade

2.2 复数响应幅值关于叶片频率失谐的灵敏度

叶盘结构整体质量失谐矩阵δM关于第j个叶片的频率失谐参数bj的第一阶导数为

(19)

整体失谐矩阵δM依次对bj和bk求导得：

(20)

式中：δjk为Kronecher符号。

将式(19)和式(20)分别代入到式(8)和式(9)得：

(21)

(22)

式中：

(23)

(24)

2.3 复数响应幅值关于节点失谐质量的灵敏度

最大响应幅值关于节点失谐质量的灵敏度系数能够给出节点响应幅值随失谐质量变化的梯度信息，有助于深入地研究失谐叶盘的动态特性以及失谐质量不确定性带来的影响。假设引入失谐的质量矩阵为集中质量。则叶盘整体失谐质量矩阵对第j个扇区的第l个节点质量的导数为

(25)

(26)

所以将式(8)和式(9)表示成对不同节点失谐质量进行求导，可以得到复数响应幅值对失谐质量的一、二阶灵敏度，即

(27)

(28)

式中：

(29)

(30)

2.1～2.3节给出的灵敏度系数计算方法直接基于高保真叶盘结构系统的减缩模型对其运动方程进行推导，未引入任何近似和简化措施，能够有效、精确地计算出失谐叶盘最大节点响应幅值关于叶片频率失谐参数和节点失谐质量的一阶和二阶灵敏度系数。

2.4 失谐叶盘受迫响应幅值灵敏度分析流程

计算失谐叶盘节点最大响应幅值关于叶片频率失谐参数和节点失谐质量的一阶和二阶灵敏度系数的流程如图 2所示。首先采用文献[16-17]给出的失谐叶盘减缩建模及动力响应计算方法计算出失谐叶盘受迫响应；然后如2.1～2.3节所示即可计算相应的灵敏度系数。其具体步骤如下：

1) 在考虑的激励阶次(EO)、分析频率范围ω-、ω+和失谐形式b下，采用文献[16-17]建立的失谐叶盘响应分析方法计算出叶盘在各个频率点下的响应参数。然后筛选出分析频率范围内叶盘结构最大节点响应幅值a以及对应的频率点ωmax和复数响应幅值xωmax。

3) 根据2.1节推导的公式，计算失谐叶盘在最大响应频率点下响应幅值关于失谐参数(叶片频率失谐或叶片节点失谐质量)的灵敏度系数，分别如式(11)和式(13)。因此，文中给出的两类灵敏度系数计算方法(① 最大节点响应幅值关于叶片频率失谐灵敏度；② 最大节点响应幅值关于叶片节点失谐质量灵敏度)分别如图2中左侧和右侧流程所示。

图2 失谐叶盘灵敏度系数分析流程图
Fig.2 Flow chart of sensitivity coefficient analysis for mistuned bladed discs

3 数值分析算例

图3 叶盘结构有限元模型
Fig.3 Finite element model of bladed disc

图4 谐调叶盘结构的频率节径图
Fig.4 Natural frequency of tuned bladed disc vs nodal diameter number

引入叶片失谐的集中质量矩阵的质量点均匀地分布在叶片的表面部分节点上，并且节点的失谐质量元素的大小与节点对应的叶片厚度成正比。单个叶片施加不同失谐水平系数倍初始失谐矩阵的失谐质量μjδΜS，然后计算叶片对应的各阶频率。通过改变不同的失谐水平系数μj多次计算，可以计算出参考阶次频率失谐参数bj与失谐水平系数μj(bj)之间的函数关系，如图1所示。实际航空发动机采用的叶片频率失谐范围一般在±5.0%之间。因此，在获取叶片频率失谐参数与失谐水平关系时，在频率失谐范围内生成一组叶片频率失谐形式，然后通过建立的关系μj(bj)求出各个叶片频率失谐对应的失谐水平系数。

图5 一组随机生成的失谐样本
Fig.5 A randomly generated mistuning pattern

图6 归一化最大节点受迫响应幅值
Fig.6 Normalized maximum forced response displacement of node

随机生成一组叶片频率失谐形式用来对该叶盘结构进行受迫响应和灵敏度计算，如图5所示。在该失谐形式和图4中标出的激励阶次和频率范围情况下(9.0～10.5 kHz，6EO)，叶盘结构最大节点受迫响应幅值随频率变化的关系曲线如图6所示。此处最大节点受迫响应幅值进行了归一化处理，即采用失谐叶盘最大响应幅值放大因子[20](失谐叶盘在各计算频率点最大响应幅值与谐调叶盘最大响应幅值之比)来表征失谐叶盘结构的振动水平。

3.1 最大响应幅值关于叶片频率失谐灵敏度

本节主要分析失谐叶盘最大响应幅值关于叶片频率失谐参数的一阶和二阶灵敏度系数。选取图 6中第1个最为显著的响应峰值点(标记为Peak)处对应的频率作为叶盘灵敏度分析算例的计算频率点。为了验证第2节提出的灵敏度计算方法的计算精度，在本节将采用差分近似法计算的一阶和二阶灵敏度系数与文中给出方法计算的灵敏度系数进行比较验证。对于失谐叶盘结构，可将其最大响应幅值视为各个叶片失谐参数的高维变量函数a(b)。因此，采用差分近似方法计算失谐叶盘最大响应幅值的一、二阶灵敏度系数可以表示为

(31)

(32)

式中：b0为初始失谐形式列向量；ej(j=1,2,…,NB)为只有第j个元素为1其他元素都为零的列向量；标量Δb为叶片频率失谐量摄动值。

失谐叶盘最大响应幅值关于叶片频率失谐的一阶灵敏度系数分布如图7所示。图中黑色柱状图(图中标记为Derivation)表示采用第2节推导的公式计算得到的灵敏度系数，而白色框图(图中标记为Approximation)表示采用数值差分近似法计算得到的灵敏度系数。从图中的灵敏度系数比较可以看出两者计算结果几乎一致。此外，叶片频率失谐的引入使得叶盘结构最大响应幅值关于各个叶片频率失谐参数的灵敏度系数也各不一样，编号为13、23和32的叶片最为敏感。

通过比较两者(文中推导方法和差分近似法)的计算效率可以看出：采用文中第2节推导出的方法只需要对失谐叶盘进行一次响应计算，然后采用文中给出的公式即可快速计算出最大响应幅值关于各个叶片频率失谐参数的灵敏度系数；而采用差分近似法计算则针对各个不同叶片频率失谐参数的灵敏度系数均需要再进行一次失谐形式摄动，并求出对应的最大响应幅值，即对于算例采用的有限元模型采用差分近似方法求解一阶灵敏度系数需要求解1+NB=49次最大响应幅值。

另外，叶盘结构最大节点响应幅值关于频率失谐参数的二阶灵敏度系数如图8所示。比较图中由本文推导方法求解的灵敏度结果(图中标记为Derivation)和由差分近似法求解的结果(图中标记为Approximation)，可以看出两者计算的灵敏度系数十分相近。显然，失谐叶盘最大响应幅值对于各叶片频率失谐参数的敏感程度差异显著。

图7 叶盘结构一阶频率失谐灵敏度
Fig.7 The 1st order sensitivity coefficients with respect to frequency mistuning of bladed disc

图8 叶盘结构二阶频率失谐灵敏度
Fig.8 The 2nd order sensitivity coefficients with respect to frequency mistuning of bladed disc

对于二阶灵敏度计算，两者的计算效率差异更为明显：采用本文给出的二阶灵敏度计算方法仅需进行一次响应计算，然后使用推导的公式即可直接计算出最大响应幅值关于各个叶片之间的二阶灵敏度系数；而采用差分近似法则需要进行1+NB(1+NB)/2=1 177 (二阶灵敏度系数矩阵为对称阵)次响应计算。

上述算例结果表明，本文提出的基于大规模高保真失谐叶盘模型的灵敏度分析方法相较于常规的数值差分近似计算方法，在计算精度和求解效率方面具有巨大的优势。

3.2 最大响应幅值关于节点失谐质量灵敏度

本节主要对叶盘结构最大响应幅值关于节点失谐质量的灵敏度系数分布进行探讨分析，在关心的分析频率范围(9.0～10.5 kHz)中，仍然选取图6中标为Peak处所在频率为分析算例的计算频率点，其激励阶次为6EO，叶片频率失谐形式如图5所示。

叶盘结构在该激励频率点处的最大节点响应幅值关于各叶片表面节点失谐质量的一阶灵敏度系数分布如图9所示。图9中比较敏感叶片的灵敏度系数的单独视图如图10所示。从灵敏度系数在叶片表面的分布来看，图10中3个灵敏度系数显著叶片的分布趋势十分相近，其主要原因在于：失谐叶盘受迫响应不再是某一阶模态单独被激发，而是多阶谐调模态贡献的结果。

为了进一步探讨失谐叶盘最大响应幅值关于各叶片表面节点失谐质量的灵敏度系数与叶片模态振型之间的关系，给出单个叶片的6～8阶模态振型，如图11所示。该算例中选取的灵敏度计算

频率点靠近叶盘结构的第6模态族，因此叶片的6阶模态对叶盘受迫响应占据了主要的贡献。此外，通过对比图10的灵敏度系数分布和图11的模态振型，可以看出：6阶叶片模态对响应占据主导作用，致使图10中各叶片的灵敏度系数分布与图11(a)中的6阶模态振型分布十分相似。

另外，该算例叶盘最大响应幅值关于各叶片表面的节点失谐质量灵敏度系数的分布柱状图如图12所示，从图中可以看出：失谐的引入使得叶盘最大响应幅值关于节点失谐质量的灵敏度系数也存在局部化现象，其中对25号叶片上的失谐质量点最为敏感。

图9 叶盘结构节点失谐质量灵敏度系数分布云图
Fig.9 Visualization of sensitivity coefficients with respect to mistuned nodal mass of bladed disc

图10 敏感叶片的节点失谐质量灵敏度系数分布云图
Fig.10 Visualization of sensitivity coefficients with respect to mistuned nodal mass for individual blades

图11 单个叶片的模态振型
Fig.11 Mode shape of a single blade

图12 叶盘结构的节点失谐质量灵敏度系数分布
Fig.12 Distribution of sensitivity coefficients with respect to mistuned nodal mass of blade disc

4 结 论

1) 本文中所提出的失谐叶盘最大响应幅值关于叶片频率失谐参数和节点失谐质量的一阶和二阶灵敏度分析方法可以有效地求解高保真失谐叶盘最大响应幅值在不同激励频段、激励阶次和失谐形式下的灵敏度系数。

2) 该灵敏度分析方法的有效性在大规模高保真失谐叶盘结构模型上得到了验证。结果表明，相较于常规的数值差分灵敏度近似计算方法，本文提出的灵敏度分析方法在计算精度和计算效率方面具有巨大的优势。

3) 该灵敏度分析方法为进一步深入开展失谐叶盘响应特性的研究提供了准确的灵敏度信息，在失谐叶盘结构布局优化设计、预测失谐参数不确定性造成的影响以及失谐叶盘结构的响应面替代模型构建等研究领域具有广阔的应用前景和通用性。

[1] 臧朝平, 兰海强. 失谐叶盘结构振动问题研究新进展[J]. 航空工程进展, 2011, 2(2): 133-142.

ZANG C P, LAN H Q. Advances in research vibration problem of mistuned blisk assemblies[J]. Advances in Aeronautical Science and Engineering, 2011, 2(2): 133-142 (in Chinese).

[2] CASTANIER M P, PIERRE C. Modeling and analysis of mistuned bladed disk vibration: Current status and emerging directions[J]. Journal of Propulsion and Power, 2006, 22(2): 384-396.

[3] PIERRE C. Mode localization and eigenvalue loci veering phenomena in disordered structures[J]. Journal of Sound and Vibration, 1988, 126(3): 485-502.

[4] SLATER J C, MINKIEWICZ G R, BLAIR A J. Forced response of bladed disk assemblies—A survey[J]. Shock and Vibration Digest, 1999, 31(1): 17-24.

[5] 王建军, 姚建尧, 李其汉. 刚度随机失谐叶盘结构概率模态特性分析[J]. 航空动力学报, 2008, 23(2): 256-262.

WANG J J, YAO J Y, LI Q H. Probability characteristics of vibratory mode of bladed disk assemblies with random stiffness mistuning[J]. Journal of Aerospace Power, 2008, 23(2): 256-262 (in Chinese).

[6] 李其汉, 王延荣, 王建军. 航空发动机叶片高周循环疲劳失效研究[J]. 航空发动机, 2003, 29(4): 16-18.

LI Q H, WANG Y R, WANG J J. Investigation of high cycle fatigue failures for the aero engine blades[J]. Aeroengine, 2003, 29(4): 16-18 (in Chinese).

[7] WHITEHEAD D S. The maximum factor by which forced vibration of blades can increase due to mistuning[J]. Journal of Engineering for Gas Turbines and Power-transactions of the ASME, 1998, 120(1): 115-119.

[8] HAUG E J, EHLE P E. Second-order design sensitivity analysis of mechanical system dynamics[J]. International Journal for Numerical Methods in Engineering, 1982, 18(11): 1699-1717.

[9] HAFTKA R T. Second-order sensitivity derivatives in structural analysis[J]. AIAA Journal, 1982, 20(12): 1765-1766.

[10] HAFTKA R T, MROZ Z. First and second order sensitivity analysis of linear and nonlinear structures[J]. AIAA Journal, 1986, 24(7): 1187-1192.

[11] KOMKOV V, CHOI K K, HAUG E J. Design sensitivity analysis of structural systems[M]∥Mathematics in Science and Engineering, Volume 177. Orlando, FL: Academic Press, 1986: 381.

[12] WANG B P. Eigenvalue sensitivity with respect to location of internal stiffness and mass attachments[J]. AIAA Journal, 1993, 31(4): 791-794.

[13] OGUAMANAM D C, LIU Z S, HANSEN J S. Natural frequency sensitivity analysis with respect to lumped mass location[J]. AIAA Journal, 1999, 37(8): 928-932.

[14] PETROV E P, IGLIN S P. Search of the worst and best mistuning patterns for vibration amplitudes of bladed disks by the optimization methods using sensitivity coefficients[C]∥Proceedings of the 1st ASSMO UK Conference, Engineering Design Optimization. Ilkley: MCB University Press, 1999.

[15] PETROV E P. A sensitivity-based method for direct stochastic analysis of nonlinear forced response for bladed disks with friction interfaces[J]. Journal of Engineering for Gas Turbines and Power, 2008, 130(2): 022503.

[16] 臧朝平, 段勇亮, E.P. PETROV. 失谐叶片轮盘的减缩建模及动力响应预测方法[J]. 航空学报, 2015, 36(10): 3305-3315.

ZANG C P, DUAN Y L, PETROV E P. Reduced-order modelling and dynamics response prediction method for mistuned bladed discs[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3305-3315 (in Chinese).

[17] DUAN Y, ZANG C, PETROV E P. Forced response analysis of high-mode vibrations for mistuned bladed disks with effective reduced-order models[J]. Journal of Engineering for Gas Turbines and Power, 2016, 138(11): 112502.

[18] YANG M T, GRIFFIN J H. A reduced-order model of mistuning using a subset of nominal system modes: 99-GT-288[R]. New York: ASME, 1999.

[19] PETROV E P, SANLITURK K Y, EWINS D J. A new method for dynamic analysis of mistuned bladed disks based on the exact relationship between tuned and mistuned systems[J]. Journal of Engineering for Gas Turbines & Power, 2002, 124(3): 586-597.

[20] 王建军, 李其汉. 航空发动机失谐叶盘振动减缩建模与应用[M]. 北京: 国防工业出版社, 2009: 1-3.

WANG J J, LI Q H. Methods and applications of reduction modeling for mistuned bladed disk in aero-engine [M]. Beijing: National Defense Industry Press, 2009: 1-3 (in Chinese).

Sensitivityanalysismethodforforcedresponseofmistunedbladeddiscs

TANYuanqiu1,ZANGChaoping1,*,ZHOUBiao1,DUANYongliang1,E.P.PETROV2

1.JiangsuProvinceKeyLaboratoryofAerospacePowerSystem,CollegeofEnergyandPowerEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China2.SchoolofEngineeringandInformatics,UniversityofSussex,BrightonBN1 9QT,UnitedKingdom

Theforcedresponseofbladeddiscsisverysensitivetorandomblademistuning.Thispaperproposesaneffectivesensitivityanalysismethodtoexploretheimpactofblademistuningparametersonthemaximumvibrationalamplitudeofmistunedbladeddiscs.Thismethodisconstructedbasedonthereduced-ordermodelandasubsequentforcedresponseanalysisofmistunedbladeddiscs.Mathematicalexpressionsofthefirstandsecondordersensitivitycoefficientsforthemaximumbladevibrationalamplitudewithrespecttobladefrequencymistuningparametersandmistuningnodalmassarederivedfromtheequationsformotionofmistunedbladeddiscs,withoutanyhypothesisornumericalsimplification.Themethodproposedcanbeusedtoperformeffectivesensitivityanalysisforbladeddiscswithanyrandomblademistuningpatternvibratingindifferentfrequencybandsunderanengineorderexcitation.Themethodisnumericallyvalidatedinahigh-fidelitymistunedbladeddiscmodel.Itisshownthattheproposedmethodhastheadvantagesofhighaccuracyandcomputationalefficiencyoverthemethodoffinitedifferenceapproximationofthesensitivitycoefficients.Benefitingfromitsversatility,themethodproposedisexpectedtofurthercontributetotheforcedresponseanalysisofmistunedbladeddiscs.

mistuning;bladeddisc;high-fidelity;sensitivityanalysis;mathematicalexpression

2017-04-06；

2017-06-19；

2017-06-27；Publishedonline2017-08-021601

URL：http://hkxb.buaa.edu.cn/CN/html/20171218.html

s：NationalNaturalScienceFoundationofChina(11372128,51175244);AeronauticalScienceFoundationofChina(20152152031)

.E-mailc.zang@nuaa.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221305

2017-04-06；退修日期2017-06-19；录用日期2017-06-27；网络出版时间2017-08-021601

http://hkxb.buaa.edu.cn/CN/html/20171218.html

国家自然科学基金(11372128,51175244)；航空科学基金(20152152031)

.E-mailc.zang@nuaa.edu.cn

谭元球，臧朝平，周标，等.失谐叶盘受迫响应的灵敏度分析方法J. 航空学报，2017,38(12):221305.TANYQ,ZANGCP,ZHOUB,etal.SensitivityanalysismethodforforcedresponseofmistunedbladeddiscsJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):221305.

V231.9

A

1000-6893(2017)12-221305-11

徐晓)