一种复杂可修系统的可用度计算方法

李军亮，滕克难，夏菲

1.海军航空工程学院 科研部，烟台 264001 2.中国人民解放军92635部队，青岛 266041 3.国网辽阳供电公司信息通信分公司，辽阳 111000

一种复杂可修系统的可用度计算方法

李军亮1, 2,*，滕克难1，夏菲3

1.海军航空工程学院 科研部，烟台 264001 2.中国人民解放军92635部队，青岛 266041 3.国网辽阳供电公司信息通信分公司，辽阳 111000

论文采用分-立的思想构建了一种复杂可修系统的可用度计算方法，即采用先分解后综合的方法来构建系统的可用度模型。分解主要是指分析系统包含的子系统和部件之间的故障行为特性，包括部件故障时间分布函数、故障传播路径、系统结构等内容，采用通用发生函数(UGF)建立了多部件系统的0-1状态可靠性评估模型，并对系统的可靠度进行分析，在此基础上将系统看作一个整体，通过更新过程理论建立故障时间和维修时间服从一般分布的系统可用度方程，给出并证明了系统可用度求解的一般方法。通过算例分析表明，论文设计方法严谨、科学，具有较强的可用性和通用性，在可靠性工程领域有很强的推广价值。

可修系统；可靠性；可用性；通用发生函数；拉氏变换

军用飞机是一种复杂的可修系统，计算其可用性时，既要准确分析飞机的可靠性，又要分析保障系统的维修性。目前常用的可用度建模方法有：随机过程理论、计算机仿真、通用发生函数(Universal Generating Function，UGF)以及三者之间的综合方法[1-22]。随机过程理论主要通过建立系统的马尔科夫方程、更新方程等方法来构建精确的系统可用度模型[4-5]，但是难以用于结构复杂的系统可用性评估；计算机仿真方法主要有蒙特卡洛仿真[6-7]、离散事件调度[8-9]等，该类方法主要通过计算机软件对部件和系统故障行为的多次模拟来实现系统可用度评估，可以准确反映系统结构的拓扑特性，但是没有精确的数学模型，而且随着系统规模的增大算法运行时间增长；UGF是拉氏变换和母函数理论在可靠性领域的推广，在计算多状态复杂系统的可靠性和可用度方面有较好的应用[11-21]，该方法既可以准确反映系统结构的拓扑特性，又可以在计算过程中通过对逻辑算子的同类项合并等操作提高运算效率，易于编程实现。传统的UGF在可用度的度量中主要通过算子δ(u(z),w)来实现，u(z)为系统实际性能状态，w为系统要求达到的性能阈值，比如“最小速度”或者“最小流量”等[11-14]，未考虑系统的维修特性；在计算系统可靠性时没有考虑系统的故障传播特性。文献[20]研究了部件维修策略对系统可用度的影响；文献[21]研究了工作共享组内部存在故障传播和覆盖时，不同结构形式对系统可靠性的影响。论文基于分立思想，采用UGF构建考虑故障传播特性的系统可靠性模型，确定系统故障时间分布函数及特征参数，然后确定系统的维修时间分布函数及特征参数，采用更新过程理论建立系统可用度方程，并且通过拉氏变换和逆变换对系统的可用度求解，进而准确分析系统的可用度。

1 基本假设和研究思路

1.1 基本假设

军用飞机是一种复杂的可修系统，其自身由多个子系统和部件组成，子系统和部件的失效存在相互影响。在计算其可靠性时，需要考虑部件、子系统、系统三者内部和之间的故障行为。

在研究过程中进行以下假设：① 发现故障则立即修理，不存在维修延时；② 系统或者部件维修时，采用完全维修策略，即修复如新[23]。

1.2 研究思路

基于以上假设，论文采用分-立的思想构建复杂可修系统的可用度计算方法，即采用先分解后综合的方法来构建系统的可用度模型。第2节采用UGF构建系统的可靠性评估模型，第3节采用更新过程理论构建系统的可用度模型，第4节完整地描述系统可用度计算的通用方法步骤，第5节通过案例分析来验证设计方法的有效性和正确性。

2 系统可靠性评估模型

2.1 UGF理论简介

UGF是现代离散数学领域的重要方法，它能以某种统一的程序方式处理求数列的表达式、求递推关系、求数列均值和方差等问题。Gregory和Anatoly等在可靠性理论应用和发展了该方法，使之成为多状态系统可靠性分析和建模的新工具[11-15]。

记单部件的离散状态变量为x，具有K种可能的状态，不同的状态记为xk,对应的概率记为qk,则部件的u函数[12]为

(1)

对于多部件系统，第j个部件的u函数可表示为

(2)

式中:xjk为部件的性能状态;qjk为对应的概率。

部件之间的u函数可通过结构算子计算，不同结构的系统算子定义如式(3)和式(4)[12]，两部件并联系统为

(3)

两部件串联系统为

(4)

系统的u函数，通过部件和子系统的u函数的复合运算得到，但传统的基于UGF的系统可靠性建模方法并未考虑系统的故障传播特性，基于此本文考虑存在故障传播的结构算子的设计。

2.2 部件之间存在故障传播时的u算子

(5)

式中：Mmax为部件i最大状态数量。

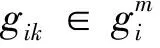
(6)

当Gj=gjc时部件的概率为

(7)

(8)

(9)

那么部件i和部件j的u函数可表示为

(10)

(11)

2.3 部件对部件组存在故障传播时的u算子定义

(12)

(13)

式中：

pnc1pjh1,pnc2pjh2,…,pncMpjhM。

2.4 系统可靠性评估

系统的u(z)可以通过子系统和部件的复合运算得到，并且利用u(z)函数的特性，对u(z)在z=1处求一阶偏导和二阶偏导，可求得系统的可靠性u函数G(t)的数学期望和方差[18-19]分别为

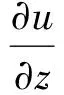
(14)

σ2(G(t))=u″+u′-(u′)2

(15)

即可得到系统的平均可靠度和方差。

3 基于更新过程的系统可用度模型

假设系统故障时间X服从一般概率分布F(t)，修理时间Y服从一般概率分布M(t)，系统在修复后，其工作寿命服从分布如新部件一样，并且X和Y相互独立，令Zα=Xα+Yα为第α个周期内的装备寿命和更新时间(α=1,2,…)，则Zα,α=1,2,…是一个服从独立同分布的随机变量序列，可构成一个更新过程，根据文献[24]可得系统的可用度方程为

A(t)=1-F(t)+Q(t)×A(t)

(16)

式中：Q(t)=P(X+Y≤t)，对式(16)进行Laplace变换可得

(17)

对于式(16)，只需确定系统的故障时间分布函数F(t)和修理时间分布函数M(t)，从而求得F(s)和M(s)，再对式(17)进行反Laplace变换即可得到系统的瞬时可用度方程A(t)为

A(t)=Lz-1A(s)

(18)

为了说明系统可用度函数A(t)存在，需证明2个问题，即A(t)的Laplace变换和逆变换的存在。

3.1 A(t)的Laplace变换存在

证明：假设装备的周期为T，Tα为第α个检查周期，则满足:

(19)

且假设在同一周期内至多有一次修理过程。则在周期Tα内，系统的可用度函数可分为以下4种情况讨论：

1) 当Xα≥Tα时

A(t)=R(t)Tα-1≤t≤Tα+1

(20)

2) 当Yα≥Tα时

A(t)=M(t)Tα-1≤t≤Tα+1

(21)

3) 当Xα+Yα≤Tα时

(22)

4) 当Xα+Yα>Tα时

(23)

式中：R(t)为可靠性函数。

由于F(t)和修理时间分布函数M(t)均为连续函数1)，则在以上4种情况下，则A(t)满足在周期Tα内分段连续，另外Tα满足式(21)时可任意划分，所以A(t)满足在t≥0的任一区间上分段连续。

由可用度定义可知A(t)≤1，当t→+∞时，存在正常数M>1，使得A(t)≤M，存在c≥0，使得A(t)≤M≤Mec t,0≤t≤+∞。

根据以上分析可知，满足Laplace变换存在附录中定理②，所以A(s)存在。

3.2 A(t)的逆Laplace变换存在

根据3.1节的证明，显而易见A(t)满足Dirichlet条件。

证明：

因为

符合Laplace逆变化存在附录中定理③，故A(t)的逆Laplace也存在。

4 复杂可修系统可用度计算方法

根据第2节和第3节的分析，设计复杂系统可用度的计算方法如图1所示，图中，λi为部件故障率，λs为系统故障率，其基本步骤设计如下：

步骤1根据系统结构绘制其可靠性框图。

步骤2分析部件、子系统和系统故障行为，分析部件失效对其他部件、子系统和系统的影响。

步骤3构建每个部件的uj(z)函数。

步骤4根据步骤2和3构建系统的us(z)函数。

步骤5求解系统的可靠度，计算系统的平均可靠度。

步骤6基于更新过程理论构建系统的可用度方程A(t)。

步骤7确定系统的故障时间和维修时间分布函数，采用拉氏变换和逆变换求解系统可用度函数A(t)。

步骤8分析计算结果，分析系统的可用度。

图1 本文方法的基本流程
Fig.1 Flow chart for proposed method

5 算例分析

假设某型飞机的某子系统由5个子部件组成，2个泵设备(部件1、2)以及3个反应器(部件3、4、5)，部件1、2并联，并与部件3、4、5组成的并联子系统串联，系统可靠性框图如图2所示。第1个泵设备(部件1)失效会引起部件3失效，第2个泵设备(部件2)失效引起部件3、4失效。因此，部件1、2存在选择性失效传播。

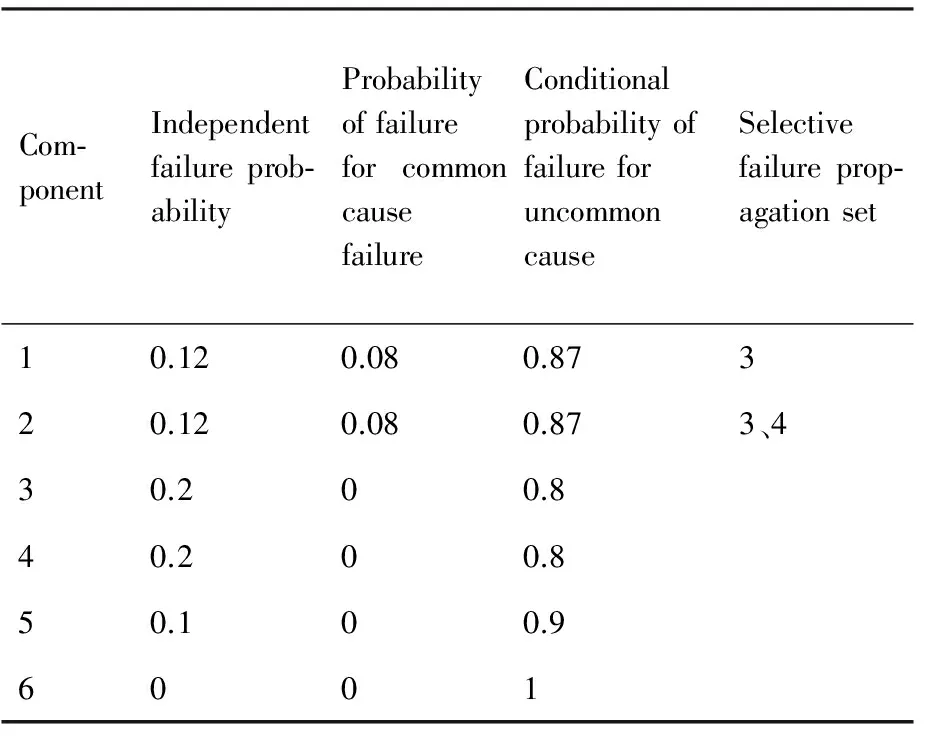
图2中，虚线箭头的指向为系统部件之间的失效传播关系。各个部件的失效概率，根据部件在使用过程中的统计数据得出，具体如表1所示。

根据表1计算部件和系统的u函数，假设部件的状态向量为xk，表达式为

(24)

则部件的为

(0.12+0.08)z0+(1-0.12-0.08)z1=

0.2z0+0.8z1

同理，可得

u2(z)=0.2z0+0.8z1

图2 系统可靠性框图
Fig.2 Block diagram of system reliability

Com⁃ponentIndependentfailureprob⁃abilityProbabilityoffailureforcommoncausefailureConditionalprobabilityoffailureforuncommoncauseSelectivefailureprop⁃agationset10．120．080．87320．120．080．873、430．200．840．200．850．100．96001

(p30+p3010×p10+p3020×p20)z0+

[1-(p30+p3010×p10+p3020×p20)]z1=

(0.2+(0.12+0.08+0.12+0.08)×0.2)z0+

{1-[0.2+(0.12+0.08+0.12+0.08)×

0.2]}z1=0.28z0+0.72z1

(p40+p4020×p20)z0+

[1-(p40+p4020×p20)]z1=

[0.2+(0.12+0.08)×0.2]z0+

{1-[0.2+(0.12+0.08)×0.2]}z1=

0.24z0+0.76z1

u5(z)=0.1z0+0.9z1

系统u函数的求解：

0.04z0+0.32z1+0.64z2

0.067 2z0+0.385 6z1+0.547 2z2

0.060 48z0+0.099 04z1+0.402 12z2+

0.494 28z3

0.100 2z0+0.381 3z1+0.573 6z2

根据据u函数的特性，利用式(14)可得

计算结果表明系统的平均可靠度大于1，是由于系统的总体结构为双余度结构。在此添加虚拟部件6，其故障行为参数如表1第7行所示，其u函数为

u10=0×z0+1×z1

则系统的u函数为

[(0.100 2+0.381 3+0.573 6)×0+

0.100 2×1]z0+(0.381 3+0.573 6)×1z1根据u函数的特性

将本文计算结果和文献[10]中的2种方法对比，其结果如表2所示。

本文设计算法计算结果介于方法1和2之间，和方法1的差值为0.008，和方法2的差值为0.005 9，平均误差为0.006 95，小于0.7%，说明论文建立的可靠性评估模型的正确性。

论文假设系统的状态为0-1状态，其状态变量为离散变量，与状态变量对应的概率分布也是离散型的；为了构建系统可用度方程，在评估系统可靠性特征参数的基础上，假设系统故障时间函数为某种已知的连续性分布形式。

文献[26-27]研究发现军用飞机在分队级保障过程中，子系统或者部件的故障时间和维修时间均服从指数分布。同样，徐宗昌对不同类型的系统维修时间分布类型进行了总结[2]，发现经过短时间调整或者迅速换件的系统维修时间适用于指数分布。

在此，假设系统的故障时间服从指数分布，则系统的平均故障率为

λs=1-E(G(t))=0.045 1

(25)

故障时间分布函数F(t)=1-exp(-λt)，其可靠性如图3所示。

同样，假设系统维修时间函数服从指数分布，分布参数为μ时，其维修时间分布函数为M(t)=1-exp(-μt)。采用论文第4节设计方法可得系

表2 由3种不同方法计算的可靠性比较Table 2 Comparisons of reliability for three methods

图3 系统的可靠度函数
Fig.3 Reliability function for system

统的可用度方程为

当维修时间分布参数变化时，系统的如图4所示。

随着μ的增加，系统的可用度提高，系统的初始时刻系统可用度最高，当系统在运行一段时间后，达到稳态可用度。

图4 维修率不同时的系统瞬时可用度
Fig.4System instantaneous availability with different value of μ

6 结 论

1) 基于UGF对0-1状态的多部件和存在失效传播的复杂系统可靠性进行了评估，并与两种不同的方法相比，平均误差小于0.7%，验证了该方法的有效性，改进并拓展了u函数理论在可靠性领域的应用；研究过程中发现采用u函数理论计算系统可靠性问题时，可以充分考虑系统结构的拓扑性和故障传播特性，评估系统的平均可靠度评估时，如果系统为多余度系统，则需要添加虚部件，对系统的u函数进行降幂处理。

2) 论文设计了一种求解复杂可修系统可用度的通用方法，并在理论上证明了该方法的正确性。

3) 在研究过程中仍然存在以下不足：一般可修系统处于运行、修理、等待的过程，论文未考虑有修理延迟的过程; 对待系统故障时间和修理时间的函数构造方法需进一步加强分析，而不仅限于常见的几种分布形式。

[1] KANG R, ZHANG Q Y, ZENG Z G. Measuring reliability under epistemic uncertainty: Review on non-probabilistic reliability metrics[J].Chinese Journal of Aeronautics, 2016, 29(3): 571-579.

[2] 徐宗昌. 保障性工程[M]. 北京: 兵器工业出版社， 2002: 50-65.

XU Z C. Supportablity engineering[M]. Beijing: Weapon Industry Press, 2002:50-65(in Chinese).

[3] 孔德良, 王少萍. 可修系统的可用度分析方法研究[J]. 北京航空航天大学学报, 2002, 28(2): 129-132.

KONG D L, WANG S P. Study on availability analysis for repairable system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(2): 129-132 (in Chinese).

[4] 王蕴, 王乃超, 马麟. 考虑备件约束的多部件串联系统使用可用度计算方法[J]. 航空学报, 2015, 36(4): 1195-1201.

WANG Y, WANG N C, MA L. Operational availability calculation methods of various series systems under the constraint of spare part[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1195-1201 (in Chinese).

[5] 杨懿, 任思超, 于永利. 均匀分布下系统瞬时可用度理论分析[J]． 北京航空航天大学学报， 2016， 42(1): 28-34．

YANG Y, REN S C, YU Y L. Theory analysis of system instantaneous availability under uniform distribution[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 28-34(in Chinese).

[6] 肖刚. 评估复杂可维修系统可靠度与瞬态可用度的蒙特卡洛方法[J]. 兵工学报, 2002, 23(2): 46-50.

XIAO G. A Monte Carlo method for obtaining reliability and availability confidence limits of complex maintenance system[J]. Acta Armamentarii, 2002, 23(2): 46-50(in Chinese).

[7] 阮渊鹏， 何桢. 基于MCS的多状态复杂系统可靠性评估[J]. 系统工程与电子技术, 2013, 35(4): 900-904.

RUAN Y P, HE Z. Reliability evaluation of complex system with common cause failures based on MCS-CA system with common cause[J]. System Engineering and Electionics, 2013, 35(4): 900-904(in Chinese).

[8] JAVIER F, ANGEL A J. Predicting availability functions in time-dependent complex systems with SAEDES simulation algorithms[J]. Reliability Engineering and System Safety, 2008, 93: 1761-1771.

[9] HINDOLO G, EDOARDO P. A hybrid load flow and event driven simulation approach to multi-state system reliability evaluation[J]. Reliability Engineering and System Safety, 2016,152: 351-367.

[10] 阮渊鹏, 何祯. 基于MCS的多状态复杂系统可靠性评估[J]. 系统工程学报, 2013, 28(3): 410-418

RUAN Y P, HE Z. Reliability evaluation of multi-state complex systems based on MCS[J]. Journal of Systems Engineering, 2013, 28(3): 410-418(in Chinese).

[11] GREGORY L, LISNIANSKI A. Importance and sensitivity analysis of multi-state systems using the universal generating function method[J]. Reliability Engineering and System Safety, 1999, 65: 271-282.

[12] GREGORY L. A universal generating function approach for the analysis of multi-state systems with dependent elements[J]. Reliability Engineering and System Safety, 2004, 84: 285-292.

[13] GREGORY L, YI D. Using inverse Lz-transform for obtaining compact stochastic model of complex power station for short-term risk evaluation[J]. Reliability Engineering and System Safety, 2016, 145: 19-27.

[14] GREGORY L, LIU D X, SUPRASAD V, et al. Reliability of non-repairable phased-mission systems with propagated failures[J]. Reliability Engineering and System Safety, 2013, 119: 218-228.

[15] ANATOLY L, DAVID E, DAVID L. A multi-state Markov model for a short-term reliability analysis of a power generating unit[J]. Reliability Engineering and System Safety, 2012, 98: 1-6.

[16] HUAN Y, JUN Y, HUADONG M. Reliability analysis of repairable multi-state system with common bus performance sharing[J]. Reliability Engineering and System Safety, 2014, 132: 90-96.

[17] LI Y F, ZIO E. A multi-state model for the reliability assessment of a distributed generation system via universal generating function[J]. Reliability Engineering and System Safety, 2012,106: 28-36.

[18] 任博, 吕震宙, 李贵杰. 基于通用生成函数的系统寿命可靠性分析[J]. 航空学报, 2013, 34(11): 2550-2556.

REN B, LYV Z Z, LI G J. Reliability analysis for system life based on universal generating function[J]. Acta Aeronautica et Astronautica sinica, 2013, 34(11): 2550-2556(in Chinese).

[19] 高鹏, 谢里阳. 基于改进发生函数方法的多状态系统可靠性分析[J]. 航空学报, 2010, 31(5): 934-939.

GAO P, XIE L Y. Reliability analysis of multi-state systems based on improved universal generating function[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 934-939(in Chinese).

[20] PENG R, XIE M, NG S H, et al. Element maintenance and allocation for linear consecutively connected systems[J]. IIE Transactions, 2012, 44(11): 964-973.

[21] PENG R, ZHAI Q, XING L, et al. Reliability analysis and optimal structure of series-parallel phased-mission systems subject to fault level coverage[J]. IIE Transactions, 2016, 48 (8): 736-746.

[22] 李军亮, 滕克难, 杨春周. 任务准备期内的军用飞机瞬时可用性研究[J]. 北京航空航天大学学报, 2017, 43(4): 754-760.

LI J L, TENG K N, YANG C Z. Research on instantaneous availability of the military aircraft during the mission preparation period[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 754-760(in Chinese).

[23] JYOTIRMOY S, SAHADEB S. Availability of a periodically inspected system under perfect repair[J]. Journal of Statistical Planning and Inference, 2000, 91: 77-90.

[24] 曹晋华, 程侃. 可靠性数学引论[M]. 北京: 科学出版社, 1986: 266-268.

CAO J H, CHEN K. Introduction to reliability mathematics[M]. Beijing: Science Press, 1986: 266-268(in Chinese).

[25] 张元林. 积分变换[M]. 3版. 北京: 高等教育出版社, 2003: 67-106.

ZHANG Y L. Integral transformation[M]. 3th ed. Beijing: Higher Education Press, 2003: 67-106(in Chinese).

[26] 徐文静. 不完全维修条件下的可用度与维修策略分析[D]. 长沙: 国防科学技术大学, 2008.

XU W J. Research on availability and maintenance policy under imperfect repair[D]. Changsha: National University of Defense Technology, 2008(in Chinese).

[27] YANG S C, LIN T W. On the application of quasi-renewal theory in optimization of imperfect maintenance policies[C]∥Reliability and Maintainability Symposium, Piscataway, NJ: IEEE Press, 2005: 410-415.

Anavailabilitycalculationmethodforcomplexrepairablesystems

LIJunliang1, 2,*,TENGKe’nan1,XIAFei3

1.NavalAeronauticalandAstronauticalUniversity,Yantai264001,China2.92635PLAForce,Qingdao266041,China3.StateGridLiaoyangElectricPowerSupplyCompany,Liaoyang111000,China

Inthispaper,anavailabilitycalculationmodelispresentedforthecomplexrepairablesystem.Themethodoffirstdecompositionbeforeintegrationisadoptedtobuildthemodelforthesystemavailability.Decompositionmainlyreferstoanalysisofthefailurebehaviorsbetweensubsystemsandcomponentsofthesystem,includingdistributionfunctionforpartsfaulttime,faultpropagationpath,systemstructure.TheUniversalGeneratingFunction(UGF)methodisusedtodevelopareliabilityassessmentmodelforthe0-1binarystatemulti-componentssystem,andthereliabilityofthesystemisanalyzed.Thegeneralsystemisthenviewedasawhole,andthesystemavailabilitymodelisbuiltbasedontherenewalprocesstheorywhenthesystemfaultandrepairtimeobeysgeneraldistribution,andageneralmethodispresentedtosolvesystemavailabilitymodel.Acasestudyispresentedtoillustratethatthedesignmethodisrigorousandscientific,andhasstrongusabilityandversatilityandthusverystrongapplicabilityinthefieldofreliabilityengineering.

repairablesystem;reliability;availability;universalgeneratingfunction;Laplacetransform

2017-02-07；

2017-03-09；

2017-04-17；Publishedonline2017-05-031644

URL：http://hkxb.buaa.edu.cn/CN/html/20171214.html

NationalDefencePre-researchFoundation(9140A27020212JB14311)

.E-mailNavy_air523@126.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221169

2017-02-07；退修日期2017-03-09；录用日期2017-04-17；网络出版时间2017-05-031644

http://hkxb.buaa.edu.cn/CN/html/20171214.html

国防预研基金(9140A27020212JB14311)

.E-mailNavy_air523@126.com

李军亮，滕克难，夏菲.一种复杂可修系统的可用度计算方法J. 航空学报，2017,38(12)：221169.LIJL,TENGKN,XIAF.AnavailabilitycalculationmethodforcomplexrepairablesystemsJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):221169.

V37;TP391.9

A

1000-6893(2017)12-221169-09

张晗)

附录

① 假设F(t)和G(t)修理时间分布函数服从某种已知的分布形式，如指数分布、正态分布、对数正态分布、威布尔分布。

② 拉氏变换存在定理

当f(t)满足以下2个条件：

1.在t≥0的任一区间上分段连续。

2.当t→+∞时，f(t)的增长不超过某一指数函数，亦即存在常数M>0及c≥0，使得

f(t)≤Mect,0≤t≤+∞,则f(t)的拉氏变换存在。

③ Laplace逆变换存在定理

拉氏逆变换的存在，满足Fourier积分定理(-∞,+∞)上满足：

1.f(t)在任一区间满足Dirichlet条件。

则存在Laplace逆变换。