一种基于特征关系式的预处理远场边界条件

李欢，陈江涛，马明生，周乃春

中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

一种基于特征关系式的预处理远场边界条件

李欢，陈江涛，马明生*，周乃春

中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

高速可压缩流动的计算方法应用于不可压低速问题会因为当地速度和当地声速量级相差较大产生刚性问题并导致数值收敛困难。预处理方法引入预处理矩阵使传统的可压缩方法具备了求解不可压或低速问题的能力。由于预处理方程改变了Navier-Stokes方程的特征值，原Navier-Stokes方程的远场边界条件不再适用。目前被广泛使用的预处理方程的远场边界条件为简化边界条件。本文以预处理方程为基础进行分析，推导了一种基于特征关系式的远场边界条件。通过典型状态算例数值实验，验证了该边界条件及预处理方法的有效性。结果显示，对于定常/非定常低速不可压流动，合理地设置远场边界条件，预处理方法都能够提高计算的收敛性和精度；对于跨声速流动，预处理方法和未加预处理方法两者的计算效率和计算精度相当。本文的预处理远场边界条件与简化预处理远场边界条件相比一是能够进一步提高计算的收敛速度；二是能够有效降低远场边界位置对预处理方法数值计算结果的负面影响。

预处理方法；Navier-Stokes方程；特征关系式；远场边界条件；数值收敛性

传统的可压缩方法在亚/跨/超声速流场数值模拟计算中迅速发展并被广泛运用，但无法有效求解低速不可压流场，导致长期以来可压缩流场与不可压缩流场采用不同的计算体系[1]。但是对于一些不可压低速流域和可压缩特性高速流域相互耦合的多种速度尺度并存的复杂流动问题，如直升机悬停状态[2-3]、大收缩比管道流[4-5]及低速大迎角流动[6-7]等，传统的不可压缩方法不能求解。而传统的可压缩方法由于稳定性限制和低速时近似因子分裂的离散误差，导致数值求解收敛困难，计算效率和计算准确性降低，甚至完全错误[8]。预处理方法通过改变Navier-Stokes方程的时间导数项使方程的特征速度在低速保持同一数量级，消除数值刚性问题，使可压缩方法能够同时求解不可压流场[9]。但由于预处理方法改变了方程的特征系统，预处理方程的无反射边界条件复杂繁琐，目前，国内外研究者[10-18]大都采用简化远场边界条件。简化的远场边界条件由于未考虑流场内信息的传播方向和物理量的守恒关系，为反射远场边界条件。反射远场边界条件数值求解收敛过程会小幅震荡，计算效率较低,只有在远场边界位置取得足够远才能够得到精度高的数值解[19]。

无反射特征线(特征关系式)法通过计算和计算域内部节点同样的物理守恒特征相容关系得到边界处未知的物理条件，是Euler方程一种准确的边界条件设定理论[20]。但目前只有少数文献[21-24]对基于特征关系式确定预处理方程远场边界条件的方法开展研究。文献[21-23]将边界面上左右两端的来流值与计算域内的值根据网格边界面上的特征值进行Roe平均确定边界值。这种方法相对于简化边界条件考虑了流场物理信息传播的方向，但不能准确描述边界值、计算域内的值和来流值的守恒关系；文献[24]以一维预处理欧拉方程为基础进行分析，将流场信息冻结在最外层网格，推导了一种物理量的守恒关系式，且考虑了流场物理信息传播的方向。但当预处理方程退化为Navier-Stokes方程时，该预处理边界条件并不能回归到原边界条件，同时作者也未具体分析该边界条件的收敛性。本文参考文献[24]的思想，在计算域的边界上将预处理方程的对流项解耦成一系列对应于相应的物理信息传播的特征波以求得边界处的未知物理条件。应用Weiss-Smith[25]预处理矩阵，从可压缩Navier-Stokes方程出发，推导基于双时间步法[26]和LU-SGS[27]隐式迭代的定常与非定常预处理方程和一种基于特征关系式的预处理方程的远场边界条件，保证远场边界条件与方程形式的映射对应关系。同时研究预处理方法在定常/非定常流场中的应用和预处理边界条件对计算收敛性和计算精度的影响。经过数值试验验证，本文基于特征关系式的预处理方程的远场边界条件能够有效降低远场边界条件位置对计算精度的影响，进一步提高预处理方法的计算效率和流场适用范围。

1 控制方程

1.1 Navier-Stokes方程

本文使用的流场解算器为自主研发的MFlow软件[28]。守恒形式的非定常可压缩Navier-Stokes方程的积分形式为

(1)

或者原始变量的非定常可压缩Navier-Stokes方程的积分形式为

(2)

式中：Ω表示控制体的体积；∂Ω表示控制体封闭面的面积；S为积分面积；Fc为无黏通量；Fv为黏性通量, 通量定义参考文献[24]；W为守恒变量；Q为原始变量；M为W与Q的转换矩阵。W、Q和M的形式为

(3)

W=[ρρuρvρwρE]T

Q=[puvwT]T

(4)

式中：u、v和w为速度在x、y和z方向的分量；cp、ρ、T、p、H和E分别为定压比热、密度、温度、压力、单位质量气体的总焓和总能量；ρp、ρT分别为密度对压力和温度的偏导数。

1.2 预处理方程

Weiss-Smith预处理矩阵用参数Θ替换式(2)中转换矩阵M中的参数ρp，得到预处理方程的形式为

(5)

式中：

(6)

(7)

式中：Ur、U∞、k和c分别为参考速度、远场来流速度、截断参数和当地声速。

由于预处理方法改变了原有控制方程组的瞬时特性，对于非定常计算，引入双时间步法进行时间推进求解。非定常预处理方程形式为

(8)

式中：t和τ分别为真实时间和虚拟时间。

2 方程离散与时间推进

非定常预处理方程左端第一项隐式离散为

(9)

式中：ΔW=Wn+1,m+1-Wn+1,m;Vol为控制单元体积;上角标m为伪时间层，上角标n为物理时间层,φ取不同的值代表不同的时间精度,φ取0为时间一阶精度，φ取1/2为时间二阶精度。

伪时间导数项显式离散为

(10)

对流通量采用隐式离散：

(11)

黏性通量采用显示离散：

(12)

式中：下角标i为单元体面序号。将式(9)～式(12)代入式(8)，控制方程经过数值离散后改写为

(13)

式中：Res为残差向量；A为雅克比矩阵，具体形式为

(14)

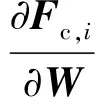
(15)

LU-SGS方法将隐式算子式(13)分解为

(D+L)D-1(D+U)ΔWn=Res

(16)

式中：因子L由严格下三角矩阵组成；U由严格上三角矩阵组成；D为对角矩阵。式(16)可以分两步求逆——前扫描和后扫描，即

(17)

(18)

(19)

(20)

由表1可知，预处理方程和Navier-Stokes方程的数值离散格式仅在矩阵J和方程特征系统的特征值λk处存在差异，而当ε=1或ε′=1时，各方程特征系统的特征值λk相同，矩阵J的形式相似，预处理方程转化为Navier-Stokes方程。因此定常/非定常预处理方程和Navier-Stokes方程在此种离散推进格式的数据结构上很相似，预处理方法易于在原Navier-Stokes方程程序上编写调试。

表1 数值离散格式对比Table 1 Comparison of numerical discretization schemes

3 远场边界条件

Weiss-Smith预处理矩阵的引入改变了原Navier-Stokes方程的的特征系统，因此原Navier-Stokes方程基于特征关系式的黎曼不变量远场边界条件需要进行预处理修正。大多数文献采用简化边界条件(Precodtioned Equation and Simplified farfield Boundary condition，PESB)。PESB采用Turkel等[29]建议的简化边界条件，亚声速入流边界速度和温度采用自由来流赋值，压强采用流场计算域内插值；亚声速出流边界速度和密度采用流场计算域内插值，压强采用流场外赋值；超声速边界所有的原始变量则根据流动方向从自由来流或者流场中赋值。

本文从一维定常预处理方程出发，推导一种基于特征关系式的远场边界条件(Precodtioned Equation and Preconditioned characteristic variable Boundary condition，PEPB)，并类推到三维定常预处理方程和三维非定常预处理方程。

式(5)忽略黏性项的微分形式为

(21)

式(21)可进一步转化为

(22)

(23)

式中：Λ为矩阵Γ-1AM的特征值组成的对角矩阵；P为矩阵Γ-1AM的左特征向量组成的矩阵。式(23)为定常预处理方程的特征相容关系式，式(23)展开形式为

(24)

(25a)

(25b)

(26a)

(26b)

式中：

(27a)

A2=ρ(λ4-εu),B2=ρ(λ5-εu)

(27b)

A2A1=1,B2B1=1

(27c)

由式(27c)可知：式(25a)和式(25b)、式(26a)和(26b)本质上具有相同的形式。文献[24]直接将A2、B2和C1冻结在计算域最外层网格单元I，得到预处理方程的3个不变量。

本文将特征相容关系式(24)进一步化简为D(p/ργ)/Dt=0,即沿特征线dx/dt=λ1，p/ργ=const1。式(25a)和式 (26a)形式复杂，直接化简不易，这里将A1和B1进一步分解为

A1=A3/ρc,B1=B3/ρc

A3=(λ4-u)/εc,B3=(λ5-u)/εc

(28)

将式(28)中的A3和B3冻结在计算域最外层网格单元I，特征相容关系式(25a)和式(26a)可以进一步化简为

(29)

(30)

式中：

A3,I=(λ4,I-uI)/(εIcI)

B3,I=(λ5,I-uI)/(εIcI)

(31)

式中：λ4,I、λ5,I、εI、cI和uI均为网格单元I的体心值。

由特征相容关系式(29)和式(30)，可以得到预处理方程的2个不变量，本文的3个不变量形式为

(32)

预处理方程特征关系式得到了与Euler方程的Riemann不变量(Riemann Invariants，RI)类似的3个不变量，定义为类黎曼不变量(Similar Riemann Invariants，SRI)。SRI、RI和文献[24]的不变量对比见表2。

表2 不变量对比Table 2 Comparison of invariants

表2中，A0、B0和C0的定义为

(33)

在ε=1时,Γ=M，预处理方程回归为Euler方程。A3,I=1，B3,I=1，SRI也与RI完全相同，本文的预处理远场边界条件回归到Euler方程的远场边界条件，保证了远场边界条件与方程形式的映射对应关系。而文献[24]中的不变量却与RI不相同，文献[24]中的预处理远场边界条件不能回归到Euler方程的远场边界条件。对于大收缩比喷管流动，大部分区域为不可压缩流动，但在入流或出流存在超声速流动，文献[24]的边界条件是不合适的；在ε≠1时，式(32)虽然是在一维定常预处理方程基础上推导得出，但很容易推广到三维定常/非定常预处理方程。由于预处理方程未改变原方程特征值的符号，因此预处理方程基于SRI推导PEPB边界条件与Euler方程采用基于Riemann不变量推导无反射边界条件(No precodtioned Equation and characteristic variable boundary condition，NE)的过程完全类似，具体参考文献[30]。

4 考核算例

4.1 无黏圆柱绕流

此算例考察预处理方法两种边界条件和未加预处理方法计算效率的差别。运用预处理方程和欧拉方程对典型算例无黏圆柱绕流进行计算，网格分布为197×61×2(周向×法向×展向)的同心圆网格。预处理方程采用两种远场边界条件：PESB和PEPB；欧拉方程采用黎曼无反射边界条件：NE。分别计算来流马赫数Ma=0.001,0.01,0.1,0.3这4个工作状态。

图1为残差收敛曲线和升力系数收敛曲线历程。其中升力系数收敛曲线历程图中NE方法的横坐标为图中上下横坐标区间，图上方横坐标为图下方横坐标迭代步数的延续；PEPB和PESB的横坐标为下横坐标。图1显示，对于Ma=0.1,0.01,0.001这3种工况，不管采用何种远场边界条件，预处理方法都能保证数值解的精度并显著改善数值解的收敛性，升力系数在15 000步已收敛至0，残值在15 000步下降了8个量级。PEPB的残值收敛历程基本无震荡，PESB的残值收敛历程震荡剧烈；不加预处理的可压缩方法(NE)不仅收敛慢，且升力系数计算结果不正确。对于工况Ma=0.1，升力系数在150 000步才能收敛至0，计算时间约为预处理方法的10倍。而对于Ma=0.01和Ma=0.001这两种工况，升力系数在150 000步和300 000步均未收敛至0，计算结果不正确。对于工况Ma=0.3，残值收敛历程预处理方法的PEPB的计算收敛速度最快，残值在15 000步依然下降了8个量级，而预处理方法的PESB的残值收敛性反而不如未加预处理方法的NE的残值收敛性。升力系数最终都能收敛到0，但NE在25 000步收敛至0，计算时间约为预处理方法的1.6倍。无黏圆柱绕流算例既考核了预处理方法高效率高精度求解无黏低速不可压流场的能力,又验证了预处理方法的PEPB能够进一步提高预处理方法的计算效率。

图1 残差收敛曲线和升力系数收敛曲线历程
Fig.1 Convergence history of residual and lift coefficients curves

4.2 Re=40的圆柱绕流

此算例考核预处理方法求解黏性流场的能力和远场边界位置对计算结果的影响。来流马赫数为0.02，Re=40的圆柱绕流尾部上下两侧会形成稳定的涡，此状态为定常状态。预处理方法仍然采用两种远场边界条件，Navier-Stokes方程为基于黎曼不变量的远场边界条件。计算网格采用同心圆网格，网格分布为113×169×2(周向×法向×展向)；壁面最小距离为0.002D(D为圆柱直径)，计算域的远场边界位置取30D(Farfield_30D)和10D(Farfield_10D)。

图2为采用PEPB计算的圆柱绕流的流线图，远场边界位置取30D(Farfield_30D)。预处理方法能够准确计算出圆柱绕流尾部上下两侧形成的稳定的涡结构。

图3为计算的壁面压力系数和实验数据[31]的对比图。表3为该流动状态的阻力系数CD和前驻点压力系数Cpf与文献计算结果的对比。由图3和表3可以清晰地看到PEPB计算的CD和Cpf与参考文献符合很好，不受远场边界位置影响；PESB计算结果受远场边界位置影响较大，在远场边界位置Farfield_30D时与参考文献符合较好；在远场边界位置Farfield_10D，计算结果与参考文献偏差较大，CD偏差约为6%，Cpf偏差约为11.5%。而不加预处理的Navier-Stokes方程计算结果与参考文献相比都存在较大偏差。

来流马赫数为0.02、Re=40的圆柱绕流算例考核了预处理方法模拟低速黏性流场的能力，只要远场边界位置选取合适，相比未加预处理方法，预处理方法计算结果更准确。如果远场边界位置取得不是足够远，采用预处理方法的PESB会对计算结果造成一定程度的偏差，但采用PEPB能够有效降低远场边界位置对计算结果的影响。

图2 圆柱绕流的流线图
Fig.2 Streamline diagram of flow around cylinder

图3 壁面压力系数对比
Fig.3 Comparison of wall pressure coefficients

=
=

计算方法CDCpfPESB＿Farfield＿30D1．5321．165PESB＿Farfield＿10D1．6271．275PEPB＿Farfield＿30D1．5111．143PEPB＿Farfield＿10D1．5361．190NE＿Farfield＿30D1．5901．180NE＿Farfield＿10D1．6711．275文献[24]1．5171．123文献[32]1．5491．147

4.3 Re=200的圆柱绕流

此算例考核预处理方法的非定常计算能力。来流马赫数为0.02、Re=200的圆柱绕流尾部会形成周期性涡脱落，此状态为非定常状态。预处理方法仍然采用两种远场边界条件，Navier-Stokes方程为基于黎曼不变量的远场边界条件。计算网格采用同心圆网格，网格分布为113×179×2(周向×法向×展向)；壁面最小距离为0.002D，计算域的远场边界位置取60D(非定常低速流动远场边界位置对结果影响较大)。真实时间步长Δt=0.002 5 s。

图4为预处理方法的PEPB计算的某一时刻马赫数等值线，预处理方法的PEPB能够捕获明显的涡脱落现象。

图5和图6为计算的升力系数和阻力系数历程(图中时间步为真实时间步)。对于升力系数历程，预处理方法的PEPB和PESB数值模拟结果基本一致，在2 000步流场达到周期谐振解；未加预处理方法在3 000步流场达到周期谐振解。对于阻力系数历程，预处理方法的PESB和未加预处理方法的NE的模拟结果的振幅不断变化，精度不高；而预处理方法的PEPB的模拟结果的周期和振幅保持不变，具有更高的计算精度。升力系数和阻力系数历程说明PESB和NE能够定性求解低速非定常流场，但时间精度和空间精度不高。表4为PEPB具体的数值结果与文献的对比，St表示斯特劳哈尔数(St=nD/U∞，n为谐振频率),St考核非定常方法的时间精度。预处理方法的PEPB的数值模拟结果和参考文献吻合得很好，说明了本文发展的预处理方法具有求解非定常流场的能力，时间精度和空间精度均较高。

图4 瞬时马赫数等值线云图
Fig.4 Contours of instantaneous Mach number

图5 升力系数历程
Fig.5 History of lift coefficients

图6 阻力系数历程
Fig.6 History of drag coefficients

=
=

计算方法CLCDStPEPB±0．681．30±0．0500．188文献[33]±0．691．31±0．0490．192文献[34]±0．661．32±0．0400．192

4.4 ONERA-M6机翼跨声速绕流

此算例考核预处理方法非结构网格求解跨声速可压缩流场的能力以及预处理方法相比未加预处理方法对跨声速可压缩流场计算结果的影响。计算的湍流模型采用S-A模型[35]，计算状态为

(34)

式中：雷诺数基于机翼的平均气动弦长。在该计算状态下，机翼表面为附着流，机翼上表面有λ型激波[36]。上表面网格分布与空间网格分布如图7所示，在激波流场特征处未有明显的加密网格。

图8为ONERA-M6机翼壁面压力系数分布对比，x/L为相对弦长，y/b为相对展长。预处理方法和未加预处理方法计算结果保持一致，说明预处理方法相比未加预处理方法对跨声速流场计算结果无影响；对于机翼下表面，数值计算结果与实验数据[37]吻合得很好；虽然上表面存在λ型激波，且计算网格分布未在激波处加密，但上表面压力系数数值计算结果与实验值仍然吻合得较好，验证了预处理方法具有求解跨声速流场的能力。

图7 ONERA-M6机翼网格
Fig.7 Grid of ONERA-M6 wing

图8 ONERA-M6机翼壁面压力系数分布对比
Fig.8 Comparison of wall surface pressure coefficients distribution of ONERA-M6 wing

5 结 论

1) 本文发展的定常/非定常预处理方程和Navier-Stokes方程在离散推进格式的数据结构上相似，预处理方法易于在原Navier-Stokes方程程序上编写调试。

2) 本文发展的基于特征关系式的预处理远场边界条件PEPB的基础是SRI(类黎曼不变量)，PEPB考虑了特征波的传播方向和守恒不变量；当预处理方程回归为原方程，SRI回归到RI(黎曼不变量)，保证了远场边界条件与方程形式的映射对应关系。

3) 对于无黏低速流场，预处理方法的求解效率高于未加预处理方法。计算的马赫数越低，未加预处理方法的计算时间成本越高。计算的马赫数越高，本文发展的PEPB的收敛效率越优于PESB。

4) 对于低雷诺数黏性低速流场，远场位置较近，PEPB比PESB的计算精度高；远场位置足够远，PEPB和PESB的计算精度保持一致。PEPB能有效降低远场边界位置对模拟结果的负面影响，节省数值计算的网格成本。

5) 对于低雷诺数黏性非定常低速流场， PEPB高于PESB和未加预处理方法的计算精度与计算效率。对于跨声速流场，预处理方法与未加预处理方法两者的求解精度相当，预处理方法对跨声速流场计算结果无影响。

本文发展了预处理方法，并在忽略黏性的基础上发展了基于特征关系式的预处理边界条件，获得类黎曼不变量。提高了预处理方法无黏低速流场的计算效率，有效降低了远场边界位置对预处理方法计算结果的负面影响。对于跨声速流动，本文发展的预处理方法具有与未加预处理方法相当的计算效率和计算精度。下一步工作一是开展预处理矩阵研究，提高预处理方法在跨声速甚至全速域流场的求解效率；二是考虑黏性的影响，进一步开展预处理方法的边界条件研究。

[1] 肖中云， 江雄， 陈作斌, 等. 低速预处理方法在悬停旋翼模拟中的应用[J]. 航空学报, 2008, 29(2): 321-326.

XIAO Z Y, JIANG X, CHEN Z B, et al. Application of low speed preconditioning to hovering rotor simulation[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 321-326 (in Chinese).

[2] POTSDAM M, SANKARAN V, PANDYA S. Unsteady low mach preconditioning with application to rotorcraft flows: AIAA-2007-4473[R]. Reston, VA: AIAA, 2007.

[3] XIAO W, SHENG C H, CHEN J P. Numerical study of preconditioned algorithm for rotational flows: AIAA-2005-5126[R]. Reston, VA: AIAA, 2005.

[4] VENKATESWARAN S, WEISS J M, MERKLE C L. Propulsion-related flowfields using the preconditioned Navier-Stokes equations: AIAA-1992-3437[R]. Reston, VA: AIAA, 1992.

[5] TOURRETTE L. Navier-Stokes simulations of air-intakes in crosswind using local preconditioning: AIAA-2002-2739[R]. Reston, VA: AIAA, 2002.

[6] 陈龙, 伍贻兆, 夏健. 基于非定常低速预处理和DES的三角翼数值模拟[J]. 南京航空航天大学学报, 2011, 43(2): 159-164.

CHEN L, WU Y Z, XIA J. Delta wing numerical simulation using unsteady low speed precondition and DES[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(2): 159-164 (in Chinese).

[7] CHOI Y H, MRKLE C L. The application of preconditioning in viscous flows[J]. Journal of Computational Physics, 1993, 105(2): 207-223.

[8] VENKATESWARAN S, MERKLE C L. Dual time stepping and preconditioning for unsteady computations: AIAA-1995-0078[R]. Reston, VA: AIAA, 1995.

[9] VENKATAKRISHNAN V. Improved convergence of compressible Navier-Stokes solvers: AIAA-1998-2967[R]. Reston, VA: AIAA, 1998.

[10] 刘中玉， 张明锋， 郑冠男, 等. 基于预处理HLLEW格式的全速域数值算法[J]. 计算物理, 2016, 33(3): 273-282.

LIU Z Y, ZHANG M F，ZHENG G N, et al. Preconditioning HLLEW scheme for flows at all Mach numbers[J]. Chinese Journal of Computational Physics, 2016, 33(3): 273-282 (in Chinese).

[11] 白晓征, 郭正, 刘君. 黏性极低速流动的预处理方法研究[J]. 空气动力学学报, 2009, 27(4): 451-455.

BAI X Z, GUO Z, LIU J. Study of preconditioning methods for very low speed viscous flows[J]. Acta Aerodynamica Sinca, 2009, 27(4): 451-455 (in Chinese).

[12] 刘晨, 王江峰, 伍贻兆. 低马赫数流动中的预处理Euler方程的收敛特性[J]. 航空学报, 2009, 30(5): 842-848.

LIU C, WANG J F, WU Y Z. Convergence characteristics of preconditioned Euler equations at low Mach numbers[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(5): 842-848 (in Chinese).

[13] 韩忠华, 宋文萍, 乔志德. 一种隐式预处理方法及其在定常和非定常流动数值模拟中的应用[J]. 计算物理, 2009, 26(5): 679-684.

HAN Z H, SONG W P, QIAO Z D. An implicit preconditioning method for steady and unsteady flows[J]. Chinese Journal of Computational Physics, 2009, 26(5): 679-684 (in Chinese).

[14] LIU Z N, RAMAKRISHNAN S V. Preconditioned upwind schemes for simulation of low speed flows on hybrid grids: AIAA-2004-1268[R]. Reston, VA: AIAA, 2004.

[15] PANDYA S A, VENKATESWARAN S. Implementation of preconditioned dual-time procedures in overflow: AIAA-2003-0072[R]. Reston, VA: AIAA, 2003.

[16] TURKEL E. Preconditioning techniques in computational fluid dynamics[J]. Annual Review of Fluid Mechanics, 1999, 31: 385-416.

[17] HAUKE G, HUGHES T J R. A comparative study of different set of variables for solving compressible and incompressible flows[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 153(1): 1-44.

[18] MERKLE C L. Preconditioning methods for viscous flow calculations[J]. Computational Fluid Dynamics Review, 1995, 153: 419-436.

[19] DARMOFAL D L. Eigenmode analysis of boundary conditions for the one-dimensional preconditioned Euler equations[M]. Cambridge, Massachusetts: Academic Press Professional, Inc., 1998.

[20] THOMPSON K W. Time-dependent boundary conditions for hyperbolic systems[M]. Cambridge, Massachusetts: Academic Press Professional, Inc., 1987.

[21] BARTH T J. Aspects of unstructured grids and finite-volume solvers for the Euler and Navier-Stokes equations[R]. Moffett Field, California: Lecture notes for the Von Karman Institute for Fluid Dy-namics Lecture Series,1994.

[22] UNRAU D，ZINGG D W. Viscous airfoil computations using local preconditioning: AIAA-1997-2027[R]. Reston, VA: AIAA, 1997.

[23] 张强， 杨永. 迎风格式的低速预处理及远场边界影响研究[J]. 西北工业大学学报, 2012, 30(3): 412-416.

ZHANG Q， YANG Y. A better preconditioning method of low Mach number flow with effects of farfield boundary conditions considered [J]. Journal of Northwestern Polytechnical University, 2012, 30(3): 412-416 (in Chinese).

[24] 肖天航, 昂海松, 余少志, 等. 预处理法求解定常/非定常混合网格的全速流场[J]. 空气动力学学报, 2007, 25(4): 425-430.

XIAO T H, ANG H S, YU S Z, et al. Using preconditioning method to simulate steady/unsteady flows at all speeds on hybrid grids[J]. Acta Aerodynamica Sinca, 2007, 25(4): 425-430 (in Chinese).

[25] WEISS J M, SMITH W A. Preconditioning applied to variable and constant density flows: AIAA-1995-0033[R]. Reston, VA: AIAA, 1995.

[26] JAMESON A. Time depended calculations using multigrid with applications to unsteady flows past airfoils and wings: AIAA-1991-1596[R]. Reston, VA: AIAA, 1991.

[27] KIM J S, KWON O J. Improvement on block LU-SGS scheme for unstructured mesh Navier-Stokes computa-tions: AIAA-2002-1061[R]. Reston, VA: AIAA, 2002.

[28] 张耀冰, 周乃春, 陈江涛. 小展弦比飞翼标模雷诺数影响数值模拟研究[J]. 空气动力学学报, 2015, 33(3): 279-288.

ZHANG Y B, ZHOU N C, CHENG J T. Numerical investigation of Reynolds number effects on a low-aspect-ratio flying-wing model[J]. Acta Aerodynamica Sinica, 2015, 33(3): 279-288 (in Chinese).

[29] TURKEL E, VATSA V N, RADESPIEL R. Preconditioning methods for low-speed flows: AIAA-1996-2460 [R]. Reston, VA: AIAA, 1996.

[30] 廖守亿, 王承尧. 预处理方法求解低马赫数流场的边界条件[J]. 国防科技大学学报, 2001, 23(2): 52-56.

LIAO S Y, WANG C Y. Boundary conditions for solving flowfields at low Mach numbers by preconditioning[J]. Journal of National University of Defense Technology, 2001, 23(2): 52-56 (in Chinese).

[31] GROVE A S, SHAIR F H, PETERSEN E E, et al. An experiment investigation of the steady separated flow past a circle cylinder[J]. Joural of Fluid Mechanics, 2006, 19(1): 60-80.

[32] ROGERS S E, KWAK D. An upwind differencing scheme for the incompressible Navier-Stokes equations: NASA-1988-101051[R]. Washington, D.C.: NASA, 1988.

[33] LIU C, ZHENG X, LIAO C. Preconditioned multigrid methods for unsteady incompressible flows: AIAA-1997-0445[R]. Reston, VA: AIAA, 1997.

[34] 牟斌, 肖中云, 刘刚, 等. 基于Roe格式的低速预处理方法研究[J]. 空气动力学学报, 2010, 28(2): 125-131.

MOU B, XIAO Z Y, LIU G, et al. Low-speed preconditioning for Roe scheme[J]. Acta Aerodynamica Sinica, 2010, 28(2): 125-131 (in Chinese).

[35] SPALART P, ALLMARAS S. A one-equation turbulence model for aerodynamic flows : AIAA-1992-0439[R]. Reston, VA: AIAA, 1992.

[36] 崔鹏程, 邓有奇, 唐静, 等. 基于伴随方程的网格自适应及误差修正[J]. 航空学报, 2016, 37(10): 2992-3002.

CUI P C, DENG Y Q, TANG J, et al. Adjoint-based grid adaptation and error correction[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 2992-3002 (in Chinese).

[37] SCHMITT V, CHARPIN F. Pressure distributions on the ONERA M6-wing at transonic mach number[R]. Paris: AGARD, 1979.

Afarfieldboundaryconditionforpreconditioningmethodbasedoncharacteristicrelations

LIHuan,CHENJiangtao,MAMingsheng*,ZHOUNaichun

ComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Duetolargedifferencebetweenlocalflowspeedandlocalsoundspeed,thenumericalmethodoriginallydevisedforcomputationofhigh-speedcompressibleflowswillsufferfromnumericalstiffproblemstoslowdowntheconvergencerate,whenthemethodisextendedtocomputationoflow-speedincompressibleflows.Afterthepreconditioningmatrixisintroduced,theoriginalmethodwillbecapableofhandlinglow-speedincompressibleproblems.However,thewidely-usedfarfieldboundaryconditionofNavier-Stokesequationsisnolongerappropriateforpreconditioningsystemssincetheeigenvaluesoftheequationsarealtered.Currently,thefarfieldboundaryconditionappliedtopreconditioningequationsismuchsimplified.Inthispaper,animprovedfarfieldboundaryconditionisproposed,whichisdevisedbasedoncharacteristicrelations.Thevalidityoftheproposedboundaryconditionisdemonstratedbyseveraltypicalcases.Itisprovedthatthepreconditioningmethodwithappropriatefarfieldboundaryconditionswillimprovetheconvergencerateandaccuracyoflow-speedincompressibleflowcomputations.Whenthepreconditioningmethodisappliedtotransonicflowproblems,theefficiencyandaccuracyofthecomputationsreachthesamelevelasthetraditionalcompressiblemethod.Theadvantagesoftheproposedfarfieldboundaryconditionoverthesimplifiedconditionlieintwoaspectstheconvergencerateisaccelerated,andthenegativeeffectofinsufficientfarfieldextentisreduced.

preconditioningmethod;Navier-Stokesequations;characteristicrelations;farfieldboundarycondition;numericalconvergencerate

2017-04-27；

2017-05-23；

2017-06-26；Publishedonline2017-07-041701

URL：http://hkxb.buaa.edu.cn/CN/html/20171206.html

.E-mailma_mingsheng@sina.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121364

2017-04-27；退修日期2017-05-23；录用日期2017-06-26；网络出版时间2017-07-041701

http://hkxb.buaa.edu.cn/CN/html/20171206.html

.E-mailma_mingsheng@sina.cn

李欢，陈江涛，马明生,等．一种基于特征关系式的预处理远场边界条件J． 航空学报,2017,38(12):121364.LIH,CHENJT,MAMS,etal.AfarfieldboundaryconditionforpreconditioningmethodbasedoncharacteristicrelationsJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):121364.

V211.3

A

1000-6893(2017)12-121364-13

李明敏)