线性变分法求解氢分子离子薛定谔方程

梁丽娜 闫彬（贵州工程应用技术学院毕节循环经济研究院，贵州 毕节 551700）

线性变分法求解氢分子离子薛定谔方程

梁丽娜 闫彬（贵州工程应用技术学院毕节循环经济研究院，贵州 毕节 551700）

用量子力学处理原子、分子等微观体系往往归结为解薛定谔方程。求解氢分子离子（H2+）的薛定谔方程在结构化学中是非常重要的内容。一般参考资料中没有给出求解H2+薛定谔方程的详细过程，造成学生学习的困难。因此本文给出了利用变分法求解薛定谔方程的详细过程。

氢分子离子；薛定谔方程；变分法?

H2＋是由两个氢原子核和一个电子组成的，可以作为讨论双原子分子的起点。分子轨道理论把H2＋作为一个整体处理，认为H2＋是一个包含两个原子核和一个电子的体系。[1]电子在两个氢核 a和b组成的平均势场中运动。H2＋的Schrödinger方程如下：

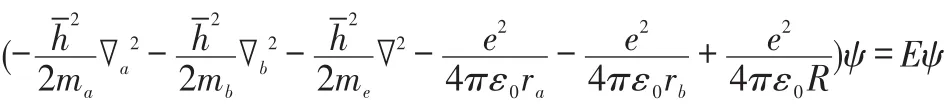
利用玻恩-奥本海默近似，H2＋的Schrödinger方程简化为：[2]

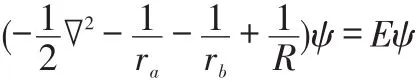
利用线性变分法[3]解上式。选择变分函数。假设分子轨道是由两个氢原子的原子轨道组成。当电子出现在氢原子核a附近时，分子轨道ψ很近似于原子轨道ψa。同样的，当这个电子出现在另外一个氢原子b附近时，分子轨道ψ也近似于原子轨道ψb。这是两种极端情况，实际上电子既属于a核也属于b核。因此y既与ya有关，又与yb有关。取其线性组合作为试探变分函数。要求其是品优波函数，单值，连续，平方可积；具有正交归一性。符合体系的边界条件：当R→∞时，ra→∞,rb→∞。

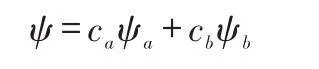
其中：ca、cb为线性组合系数，也是待定参数。[4]ψa、ψb分别为氢原子a、b的原子轨道波函数。

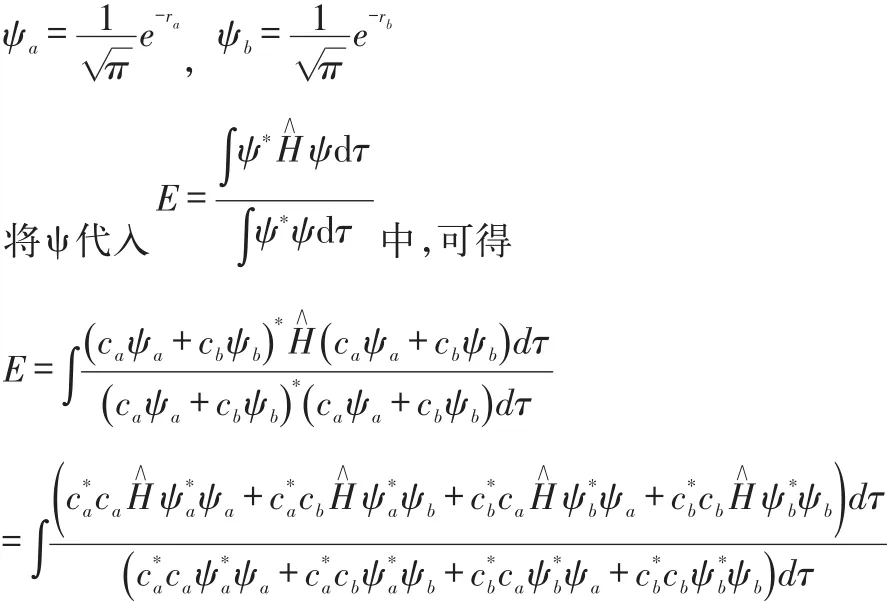
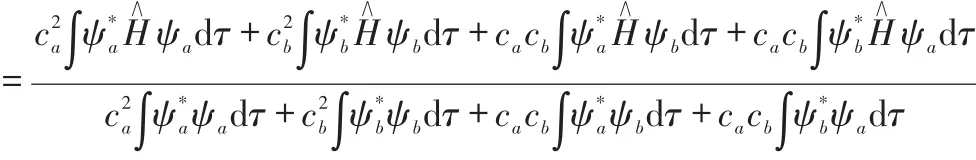
由于H2＋的两个核是等同的，并且ψa、ψb都是归一化函数，则可令

则有：

利用E取极值的条件，等式同时消去Y，并将方程组按ca、cb为未知数整理得：

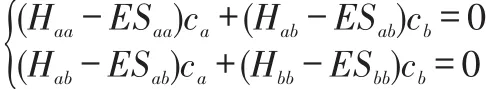
上式即为H2＋的久期方程[5]。它是关于ca、cb的线性齐次方程组。系数行列式为0时，式才有非零解。即：

由以上两式可得：

解此行列式，

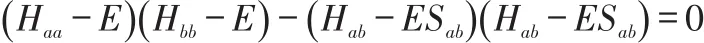
同核双原子分子

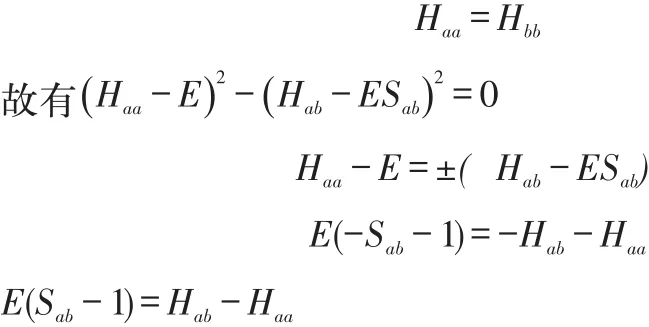
得到E的两个解：

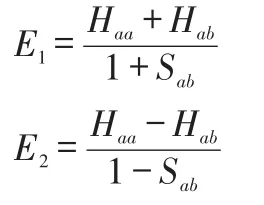
将E1代入H2＋的久期方程：

两边同时乘以（1+Sab），

将E1代入H2＋的久期方程：

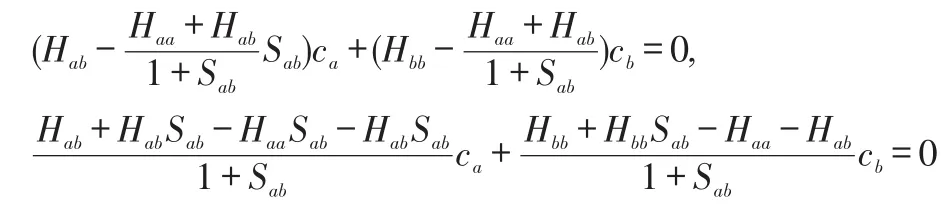
两边同时乘以1+Sab，并带入ψ1，

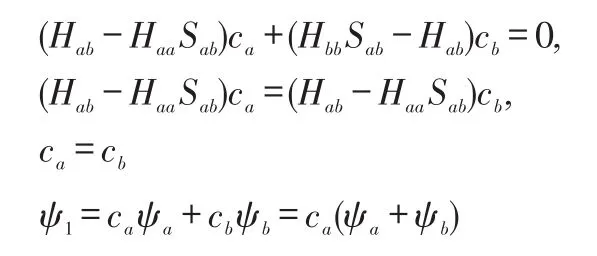
利用波函数归一化条件，可得：

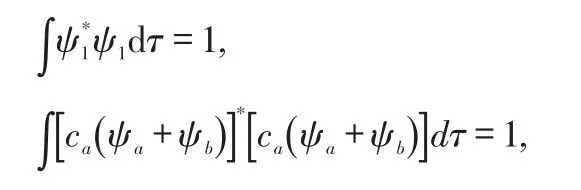
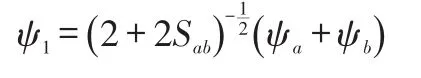
将E2代入H2＋的久期方程：

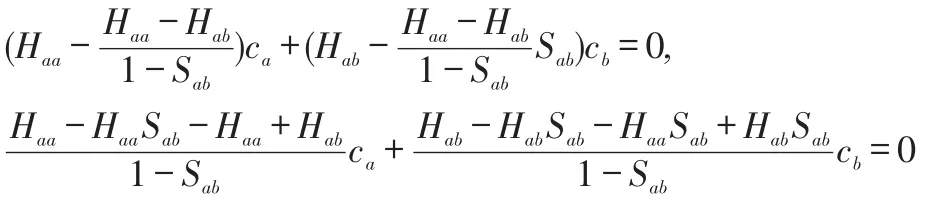
两边同时乘以1-Sab，并带入ψ1，

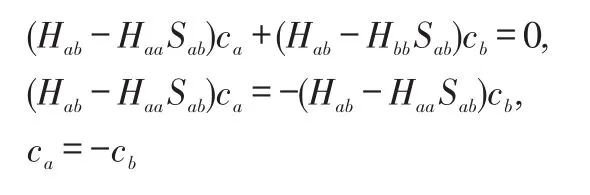
利用波函数归一化条件，可得：

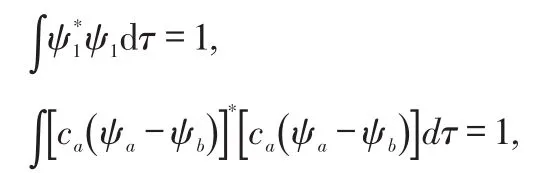
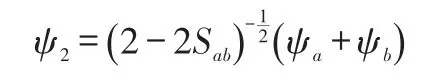
我们利用线性变分法解氢分子离子的薛定谔方程得到以下解：

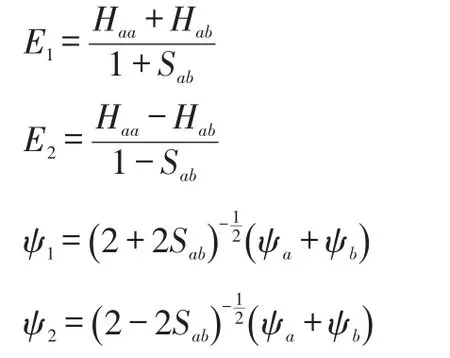
ψ1的能量E1要比1s轨道的能量低，所以当电子从氢原子的1s轨道进入ψ1时，体系的总能量降低，故ψ1为成键轨道。而当电子进入ψ2时，氢分子离子的能量E2要比原来的氢分子和氢离子的总能量高，所以ψ2就为反键轨道。

[1]申泮文.无机化学[M].化学工业出版社,2002.1.

[2]北京师范大学,华中师范大学,南京师范大学.无机化学(第四版)[M].高等教育出版社,2002.8.

[3]赵成大,郑载兴,潘道皑.物质结构[M].人民教育出版社,2004.6.

[4]马树人,何雁.结构化学基础[M].华东理工大学出版社,1994.10.

[5]刘靖疆.基础量子化学与应用[M].高等教育出版社,2004.6.