船型技术经济评价方法比较研究

张明霞 姜哲伦 徐晓丽

（1.大连理工大学 船舶工程学院 大连116024；2.中国船舶重工集团公司经济研究中心 北京100120）

船型技术经济评价方法比较研究

张明霞1姜哲伦1徐晓丽2

（1.大连理工大学 船舶工程学院 大连116024；2.中国船舶重工集团公司经济研究中心 北京100120）

船型选型问题是典型的多目标决策问题，传统的评价方法（如层次分析法、模糊综合评价法）以及由这两种方法衍生出来的模糊层次分析法在船舶技术经济评价中多有应用，而改进复合权重TOPSIS法在船舶技术经济评价问题中却应用较少。该文主要将上述4种方法从原理、特点方面进行比较，结合8艘修井船实例，通过各方法评价结果对照得到各方法的优势与劣势，对船型技术经济评价问题应该如何选择适合的评价方法给出相关建议。

层次分析法；模糊综合评价法；模糊层次分析法；改进复合权重TOPSIS法；船型技术经济论证

引 言

作为一类生产周期长、资源耗费巨大、单件小批量生产的产品，船舶的方案设计更要充分体现技术的先进性和经济的合理性，那么就要求设计者在方案初始设计阶段，对各可行方案进行科学合理的技术经济论证。如此，评价方法的优劣将直接影响决策者的判断，因而对传统方法及衍生法的特点及优劣的研究就十分必要了。

层次分析法（Analysis Hierarchy Process，AHP）、模糊综合评价法（Fuzzy Comprehensive Evaluation，FCE）及模糊层次分析法（Fuzzy Analytical Hierarchy Process，FAHP）在船舶领域应用广泛。李劲松［1］、汪敏［2］、姚雷［3］等人采用层次分析法分析船型方案的多目标决策问题，指出层次分析法具有思路简单明了，不需要建立复杂的教学模型，层次清楚，计算简单的特点［1］；刘元丰［4］、高丹［5］等人将模糊综合评价法分别应用于船舶航行安全评价、船舶溢油事故定级方面，验证了模糊综合评价法的适用性 ；黄志［6］、俎秀花［7］、周晓洁［8］等人利用模糊层次分析法分析船舶安全状况评价、船舶机舱综合评价、船舶热源系统优选问题中，得出模糊层次分析法具有能够将客观与主观结合起来，将一些模糊概念进行量化的特点［7］。改进复合权重TOPSIS法（Improved Composite Weight and TOPSIS Evaluation，ICW-TOPSIS）在船舶领域极少应用，熊云峰［9］建立了基于复合权重TOPSIS 的船舶性能综合评价方法，指出该方法具有原理简单、算法简捷、科学实用的特点；李晓伟［10］、张爱美［11］等人分别将复合权重TOPSIS法应用在公路建设项目评价、化工企业环境绩效评价方面，验证该方法的可行性。

船舶的设计受船东、设计人员的主观意愿影响较大，因此，本文选择层次分析法、模糊综合评价法、模糊层次分析法和改进复合权重TOPSIS法这4种能够反映决策者主观意愿的方法进行比较分析。

1 层次分析法

层次分析法是将与决策有关的元素分解成目标、效果、指标等层次，并在此基础上进行定性和定量分析，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策。

1.1 构造判断矩阵

层次分析法模型结构由上到下分为目标层G、一个或多个准则层C和方案层P，称之为递阶层次模型；为表述每一层中各要素对应其上层某要素的相对重要程度，构造判断矩阵如下：

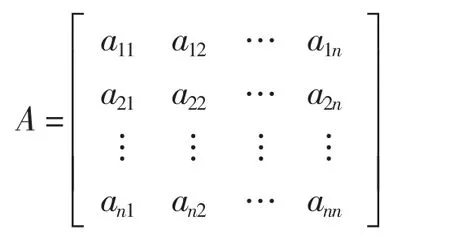
其中，aij为针对Ck而言，要素Ai相对Aj重要程度的数值，即重要性的标度。通常采用1~9比较标度［2］。为检验各元素重要度之间的协调性，判断矩阵A需经一致性检验［2］，若A不满足一致性，还需对其进行调整，直到满意为止。

1.2 指标权重计算

判断矩阵A通过一致性检验后，根据A计算该层次要素关于相邻上一层次要素Ck的优先权重，称为单层次排序。单层次排序可以归结为计算判断矩阵A最大特征值λmax所对应的特征向量W，即满足AW=λmaxW，特征向量W1=（w1，w2， …，wn）T，作为该层次n个要素的优先权重向量。常用方根法计算特征向量［2］。

若准则层层数大于1层，需要进行层次总排序，即在各层单排序基础上，从上到下逐层排序。假定层次结构模型包含2层准则层，模型设为目标层G、准则层C1、准则层C2和方案层A1。准则层C1各要素C11、C12、…、C1k对于目标层G的单排序已完成，其数值分别为w1,1、w1,2、…、w1,k；且准则层C2各要素C21、C22、…、C2n对Cj（j=1，2，…，k）的层次单排序结果是w21,j、w22,j、…、w2n,j，则层次总排序如下页表1所示。

1.3 构建标准化决策矩阵

设U={U1，U2，……，Um}为方案集，其中Ui代表第i（0＜i≤m）个可行的方案，每个方案的评价指标集设为P={P1，P2，……，Pn}，用xij表示第i（0＜i≤m）个方案的第j（0＜j≤n）个评价指标值，可以建立初始决策矩阵B={xij|i=1，2，…，m；j=1，2，…，n}见式（1）。

表1 层次总排序

评价指标通常分为两类：一类是值越大越好的效益型指标，另一类是值越小越好的消耗型指标。同时，指标间具有不同的量纲与数量级，不具有一致的可比性。为消除指标的这一问题，需要对指标矩阵进行标准化处理。

首先需对评价指标分别进行无量纲处理，公式如下：

对于收益性指标，为

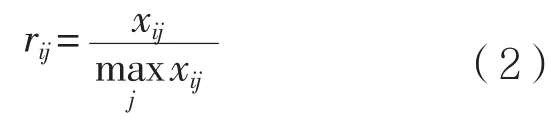
对于消耗性指标，为

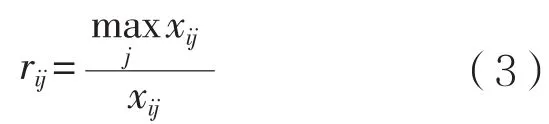
接着进行归一化处理：

则最终得到的标准化决策矩阵R1为：

1.4 方案评价排序

计算得到层次总排序之后，得到指标权重向量W1=（w1，w2， …，wn）T，则各方案的最终得分由式（6）得到：

2 模糊综合评判法

船型方案选择往往涉及若干相互制约的质量指标和很多复杂的影响因素。为获得一个理想的方案，设计者常常设计许多方案，然后进行综合分析和考虑，进行方案优选和排列。在这一过程中，设计者的经验和观点，船东的要求和意愿等，起着很重要的作用。但是，这些经验、观点、要求、意愿等，往往具有模糊性。在船型方案选择中，如何将这种模糊性加以解析化和定量化是个十分重要的问题，模糊综合评判方法是处理此类问题的一种可行方法。

2.1 定义方案集

由若干个被评判的船型方案（或设计方案）构成方案集V=（V1，V2，…，Vm）。

2.2 选择评定指标（因素）

选取表征船型方案（或设计方案）质量优劣的指标（因素），作为评判依据，组成指标集（或称因素集），记为U=（U1，U2，…，Un）。

2.3 对评定指标（因素）考评

船型方案（或设计方案）每项指标i，总是存在一个期望值Mi和允许值mi，于是就有一个允许取值区间，记为 ［mi，Mi］。设在该区间上定义一个相应于最优值的模糊子集Ai，即

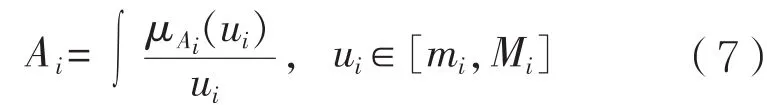
评定船型方案的每项评定指标通过方案的技术与营运经济性能计算获得。一个评定指标值经满意度函数计算后，就可给出一个模糊评定（或评分）。对各方案的各项评定指标分别进行考评，可得评判矩阵：

矩阵R2中每一行，是对船型方案某项评定指标的具体评定结果，是相对于某个统一标准的一个评分。矩阵R2中的每一列，是对某船型方案各项评定指标的评分。

2.4 进行综合评判

如前所述，船型方案确定涉及若干互相制约的评定指标和许多复杂的影响因子，因此，完成了对各评定指标单因素评定后，尚需进行多因素的综合评判。这里引入“重要度”这一概念来处理，重要度记为W2=（wu1，wu2， …，wun），其表征着对船型方案各评定指标重要程度作出评定。

确定了对各评定标准满意度和重要度的评定以后，综合评判问题归结为：

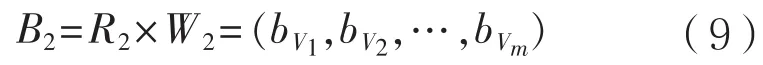
根据bVi的大小，可以完成各方案的排序，从而找出满意的方案。

3 模糊层次分析法

模糊层次分析法是层次分析法与模糊综合评价法相结合的衍生法，原理是将层次分析法计算得到的指标权重向量W1（见1.2节）与模糊综合评价法计算得到的评判矩阵R2（见式（8））相乘，见式（10）：

从而得到各方案得分。

4 改进复合权重TOPSIS法

为兼顾主观意愿和客观事实，本方法将层次分析法和熵权法以动态方式结合，构成改进复合权重，并将其与TOPSIS法理论结合，对方案进行综合评价［13］。

假设某评价问题有m个评价对象和n个评价指标，假设通过层次分析法（AHP）确定的第j个指标的权重为ωj，通过熵权法（EVM）确定的第j个指标的权重为θj，又假设决策者以εj的风险偏好倾向于使用层次分析法确定的权重，以（1-εj）的风险偏好倾向于使用熵权法确定的权重。

4.1 改进复合权重

4.1.1 层次分析法权重系数

层次分析法权重向量W计算方法可参见1.2节所述。

4.1.2 熵权法权重系数的获取

熵权法（EVM）是一类根据决策矩阵数据特点得到的客观赋权法，优势在于该方法能够最大程度利用决策矩阵的结构信息，分析出各目标的权系数值，EVM适用于评价对象间彼此相关性很小或不相关的情况。

根据指标矩阵计算熵Ej：

式中：i=1，2，…，m；j=1，2，…，n（m和n的定义见上文）；K>0，K=1/ln（n）（ln为自然对数），K为常系数；xij见2.1定义；Ej代表第j个指标的熵值，且有Ej∈［0，1］。

定义fj为各方案在第j个评价指标下贡献度的一致性程度：

因此，第j个评价指标标准化的熵权法权重系数值为：

4.1.3 改进复合权重计算

上面已经求出层次分析法权重系数ωj与熵权法权重系数θj，于是，复合权重ρj可表示为：

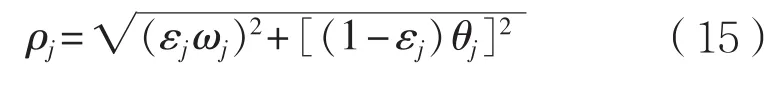
为确定εj的值，可用最小二乘法建立如下规划模型：

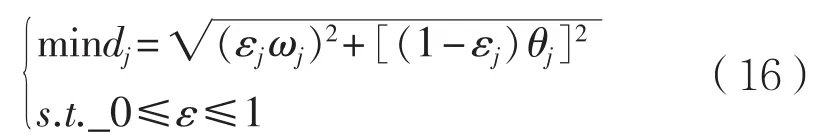
经求解，可得动态的权重偏好系数εj：

4.2 建立改进复合权重TOPSIS综合评判模型

逼近理想解排序法（TOPSIS）的基本原理是借助多目标决策问题中的正理想解和负理想解的相对距离来对评价方案进行排序。正理想解通常是虚构出来的一个最佳方案，它的每一个指标都取为待评价方案中的最优值；相对的，负理想解的指标则是待评价方案中的最劣值。TOPSIS通过考量方案对于正理想解和负理想解的趋近程度对方案进行综合排序，显然，方案越趋近正理想解越优。

4.2.1 构建标准化决策矩阵

决策矩阵标准化与层次分析法相同，见第1.3节。

4.2.2 贴近度分析

由于在决策矩阵标准化的过程中，收益性指标和消耗性指标的评价标准已经修正为一致的，即指标值都越大越优，因此，正理想解为决策矩阵R中各行向量的最大值构成的方案，负理想解则取决策矩阵R中各行向量的最小值，表达式为：

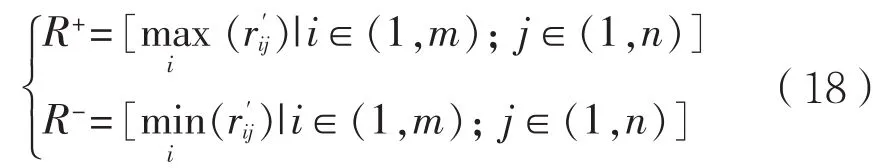
式中：R+与R-分别为正理想解和负理想解。

则各评价方案与正负理想解的距离分别表示为：

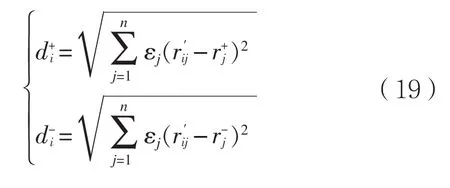
则贴近度ci的计算公式即可表达为：

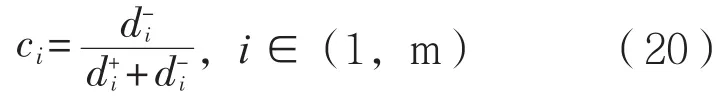
显然，待评价方案的贴近度取值为（0，1），越接近1说明其距离负理想解的相对距离越远，方案越优。

5 算 例

完井修井船是一类高技术含量、高附加值、造价高昂的海洋工程船舶，主要用于海上油田的维护、集油树的安装和拆卸等，服务于海洋石油开采工作。而目前，国内对于完井修井船的设计、建造尚处于起步阶段，技术、经验尚且不足，因此，需要与国际上现有的完井修井船进行比较排序，本文选择8艘完井修井船进行技术经济性论证，8艘船分别是深海半潜式完井修井船、 Havila Harmony、Akofs Seafarer、Helix 534、Skandi Constructor、 Island Wellserver、 Island Frontier、Well Enhancer，完井修井船主尺度见下页表2。

综合考虑完井修井船的工作性能与绿色度要求，建立最大钩载系数（RH）、作业水深系数（RDW）、可变载荷系数（RF）、单位进尺油耗（RQ）、海军部系数（RE）、EEDI这6个评价指标，其中单位进尺油耗（RQ）、EEDI是消耗型指标，值越小越好，其他指标为效益型指标，值越大越好。经计算得到完井修井船指标值见下页表3。

下面分别用上述4种方法进行方案评价、排序，各方法分别采用5~6组不同的权重系数，研究不同方法的权重系数对方案排序的影响。

5.1 层次分析法（AHP）

李劲松［1］、汪敏［2］、姚雷［3］等人分别采用层次分析法对高速客船、游览船、水面舰艇进行技术经济分析，发现该方法不仅可以得到最优方案，而且可以得到各方案的优先次序，能反映众多专家的意见，适用于船型方案决策问题。

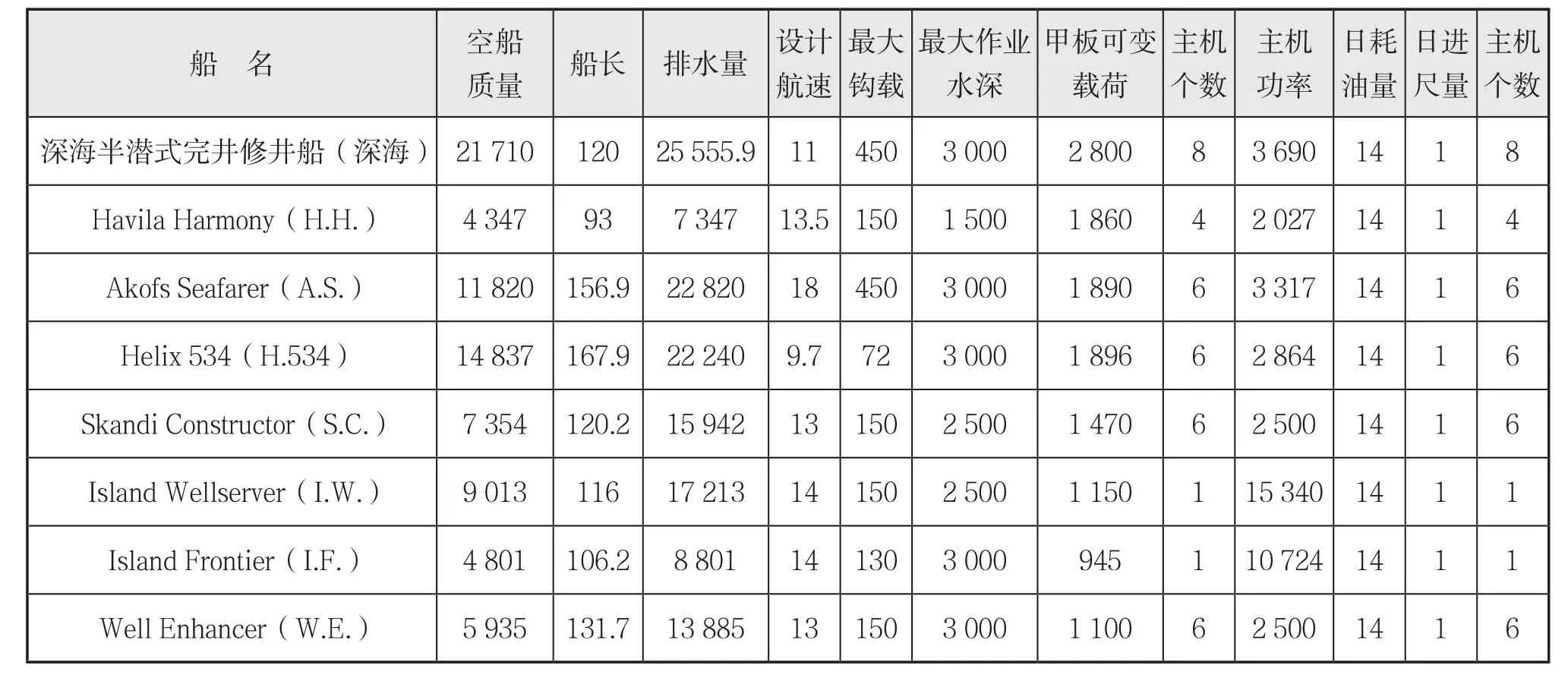
表2 修井船主尺度

表3 修井船各项指标初始数据

5.1.1 指标重要度

定义RH、RDW、RF、RQ为主要指标，RE、EEDI为次要指标，共设6组指标重要度如下：

1-RDW=RF>RH=RQ>RE>EEDI

2-RH=RF>RDW=RQ>RE>EEDI

3-RH=RDW>RF=RQ>RE>EEDI

4-RDW=RF>RH=RQ>EEDI>RE

5-RH=RF>RDW=RQ>EEDI>RE

6-RH=RDW>RF=RQ>EEDI>RE

以第一组指标重要度为例，建立相应的判断矩阵A1如下：

经计算，A1通过一致性检验，其他5组的判断矩阵同样也通过了一致性检验。

5.1.2 指标权重向量

计算得到 6组指标（RH，RDW，RF，RQ，RE，EEDI）权重向量W分别为：

AHP-1=（0.155 9，0.292 3，0.292 3，0.155 9，0.074 1，0.029 5）；

AHP-2=（0.292 3，0.155 9，0.292 3，0.155 9，0.074 1，0.029 5）；

AHP-3=（0.292 3，0.292 3，0.155 9，0.155 9，0.074 1，0.029 5）；

AHP-4=（0.155 9，0.292 3，0.292 3，0.155 9，0.029 5，0.074 1）；

AHP-5=（0.292 3，0.155 9，0.292 3，0.155 9，0.029 5，0.074 1）；

AHP-6=（0.292 3，0.292 3，0.155 9，0.155 9，0.029 5，0.074 1）。

5.1.3 计算结果及分析

由式（1）— 式（5）得到标准化判断矩阵，将其与权重向量分别带入式（6），得到层次分析法计算结果见表4、图1。

表4 层次分析法评价得分汇总

图1 层次分析法评价结果

（1）从图1中可以看出，在层次分析法中，当指标权重发生改变时，各方案得分也会发生改变。

（2）在6组指标权重下，H.H.船、A.S.船、H.534船的最高分与最低分的分差较大，分别为0.021、0.018、0.016，而S.C.船的得分变动最小，为0.002。

（3）说明H.H.船对指标权重的改变最敏感，而S.C.船对指标权重的改变不敏感。

（4）H.H.船、A.S.船随着指标权重的不同，评价得分的高低也有变化。其中，当指标权重取AHP-3时，A.S.船得分高于H.H.，其他权重下，H.H.船均高于A.S.船，说明A.S.船的最大钩载系数（RH）、作业水深系数（RDW）这两个指标组合起来最优，而H.H.的作业水深系数（RDW）、可变载荷系数（RF）和最大钩载系数（RH）、可变载荷系数（RF）的组合是最优的。

（5）H.534船在6组权重系数下，得分均为最低，说明该船技术、经济指标较差；S.C.船在6组指标权重系数下，得分基本接近，说明该船各项技术、经济指标比较均衡，既不太优秀，也不太差。

5.2 模糊综合评价法（FCE）

刘元丰［4］、高丹［5］等人将模糊综合评价法分别应用与船舶航行安全评价、船舶溢油事故定级方面，发现本方法将各种指标系统化、具体化，具有较好的可信度、效率高的特点，适用于船型方案决策问题。

5.2.1 指标取值范围

模糊综合评价法中，容许值表示某类船舶某一指标可取的最差值，即该指标的下限，期望值表示某类船舶某一指标可取的最优值，即该指标的上限。为确定各指标的容许值、期望值，需要所有方案每个指标的最大值、最小值见表5（由表2方案初始数据得到）。

表5 修井船指标最大值、最小值

对于效益型指标（RH、RDW、RF、RE）设定容许值为所有方案中该项指标最小值的95%，期望值为最大值的105%，对于成本型指标（RQ、EEDI），设定容许值为最大值的105%，期望值为最小值的95%。

5.2.2 设计满意度函数

对于效益型指标（最大钩载系数、作业水深系数、可变载荷系数、海军部系数）：

对于成本型指标（单位进尺油耗、EEDI）：

5.2.3 计算结果及分析

现根据评价指标侧重点不同建立几组权重不同的模糊综合评价模型，这些模型分别反映了五个（RH、RF、RDW、RE、EEDI）影响船舶作业性能的指标对待评价船的排序的影响。

5 组指标（RH，RDW，RF，RQ，RE，EEDI）权重分别为：

FCE-1=（0.35，0.15，0.15，0.1，0.15，0.1）；

FCE-2=（0.15，0.35，0.15，0.1，0.15，0.1）；

FCE-3=（0.15，0.15，0.35，0.1，0.15，0.1）；

FCE-4=（0.15，0.15，0.15，0.1，0.35，0.1）；

FCE-5=（0.15，0.15，0.15，0.1，0.1，0.35）。

由式（7）、式（8）得到决策矩阵，将其与权重向量分别带入式（9），得到模糊综合评价法计算结果见表6、图2：

（1）从图2中可以看出，在模糊综合评价法中，当指标权重发生改变时，各方案得分均发生较大变化。

（2）8艘船的得分曲线趋势近乎一致，只是H.H.船与A.S. 船得分高低有变化。

（3）当指标权重取FCE-2时，A.S.船得分低于H.H. 船；其他权重下，H.H. 船均低于A.S. 船。说明A.S. 船的可变载荷系数（RF）指标较差，最大钩载系数（RH）、作业水深系数（RDW）、海军部系数（RE）、EEDI指标均较好，而H.H.船的可变载荷系数（RF）指标较好，最大钩载系数（RH）、作业水深系数（RDW）、海军部系数（RE）、EEDI指标一般。

表6 模糊综合评价法评价得分汇总

图2 模糊综合评价法计算结果

5.3 模糊层次分析法（FAHP）

黄志［6］、俎秀花［7］以及周晓洁［8］等人在利用模糊层次分析法分析船舶安全状况评价、船舶机舱综合评价以及船舶热源系统优选的问题中，得出模糊层次分析法具有能够将客观与主观结合起来，将一些模糊概念进行量化的特点［7］，适用于船型方案决策问题。

（1）指标取值范围与满意度函数与5.2节相同，权重向量与5.1.2节相同。

（2）计算结果及分析

由式（10）计算模糊层次分析法计算结果，如下页表7、图3所示：

① 从图3中可以看出，在模糊层次分析法中，当指标权重发生改变时，各方案得分的变化程度介于层次分析法与模糊综合评价法之间。

② 6个指标权重下，I.F.船与H.H.船得分变化较大，分差分别为0.149、0.144，且两者相对顺序有明显变化，说明I.F.船、H.H.船对指标权重改变较为敏感；深海船、S.C.船、I.W.船的得分变化相差较小，分别为0.034、0.048、0.048，说明深海船、S.C.船、I.W.船对指标权重改变不敏感。

③ 当指标权重取FAHP-3、FAHP-6时，A.S.船得分高于H.H.船，其他权重下，H.H.船均高于A.S.船，说明A.S.船的最大钩载系数（RH）、作业水深系数（RDW）指标组合起来最优，而H.H.船的作业水深系数（RDW）、可变载荷系数（RF）或最大钩载系数（RH）、可变载荷系数（RF）的组合最优。

表7 模糊层次分析法评价得分汇总

图3 模糊层次分析法计算结果

5.4 改进复合权重TOPSIS（ICW-TOPSIS）

5.4.1 改进复合权重计算

按照4.1节中方法，其中层次分析法权重与5.1节中的相同，结合式（11）— 式（17），计算得到6 组指标（RH，RDW，RF，RQ，RE，EEDI）改进复合权重分别为：

ICW-TOPSIS-1=（0.177 6，0.259 7，0.228 5，0.197 0，0.090 5，0.046 6）；

ICW-TOPSIS-2=（0.227 2，0.198 8，0.233 2，0.201 0，0.092 3，0.047 6）；

ICW-TOPSIS-3=（0.223 3，0.260 5，0.181 1，0.197 5，0.090 7，0.046 8）；

ICW-TOPSIS-4=（0.174 5，0.255 1，0.224 4，0.193 4，0.043 9，0.108 6）；

ICW-TOPSIS-5=（0.223 0，0.195 2，0.228 9，0.197 3，0.044 8，0.110 8）；ICW-TOPSIS-6=（0.219 3，0.255 8，0.177 9，0.194 0，0.044 1，0.109 0）。

5.4.2 贴近度计算结果

由式（18）— 式（20），计算各方案的贴近度如表8、图4所示。

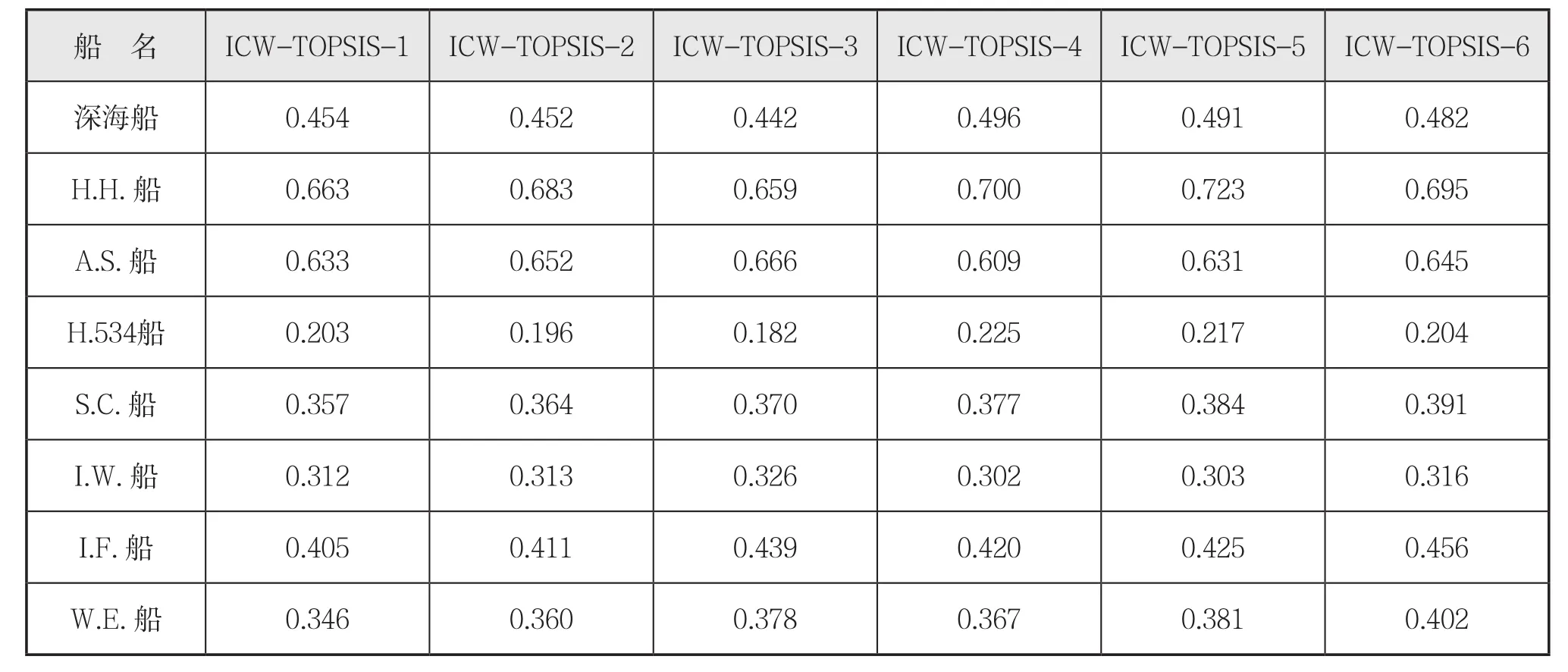
表8 改进复合权重TOPSIS评价得分汇总

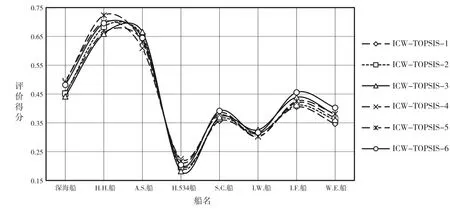
图4 改进复合权重TOPSIS法计算结果

（1）从图4中可以看出，在改进复合权重TOPSIS法中，当指标权重发生改变时，各方案得分的变化小。

（2）6个指标权重下H.H.船与A.S.船得分变化较大，分差分别为0.064 4、0.056 9，说明H.H.船与A.S.船对指标权重改变敏感；H.534船、S.C.船、I.W.船的得分变化相差较小，分差分别为0.0428、0.034 5、0.024，说明H.534船、S.C.船、I.W.船对指标权重改变不敏感。

（3）指标权重取ICW-TOPSIS-1、ICW-TOPSIS-2、ICW-TOPSIS-3时，H.H.船的评价得分分别等于、大于、小于A.S.船的评价得分，说明H.H.船的最大钩载系数（RH）、可变载荷系数（RF）指标组合起来最优，A.S.船的最大钩载系数（RH）、作业水深系数（RDW）指标组合起来最优。

5.5 三种方法结果汇总比较

下面分别讨论在同样的指标重要度情况下，各评价方法对8艘船评价得分的区别。由于层次分析法、模糊层次分析法、改进复合权重TOPSIS法的6组指标重要度一致，其中层次分析法、模糊层次分析法中6组指标权重向量均由层次分析法的判断矩阵算得，改进复合权重TOPSIS法中6组指标权重向量由层次分析法的判断矩阵结合熵权法复合得到；而模糊综合评价法中指标重要度定义与上述三种方法不同，通过自定义的方式得到5组指标权重向量，因而只对层次分析法、模糊层次分析法、改进复合权重TOPSIS法进行综合比较分析。

表9、图5为指标权重1下，层次分析法、模糊层次分析法、改进复合权重TOPSIS法的方案评价得分结果及曲线。

表9 三种方法方案评价得分——指标权重1

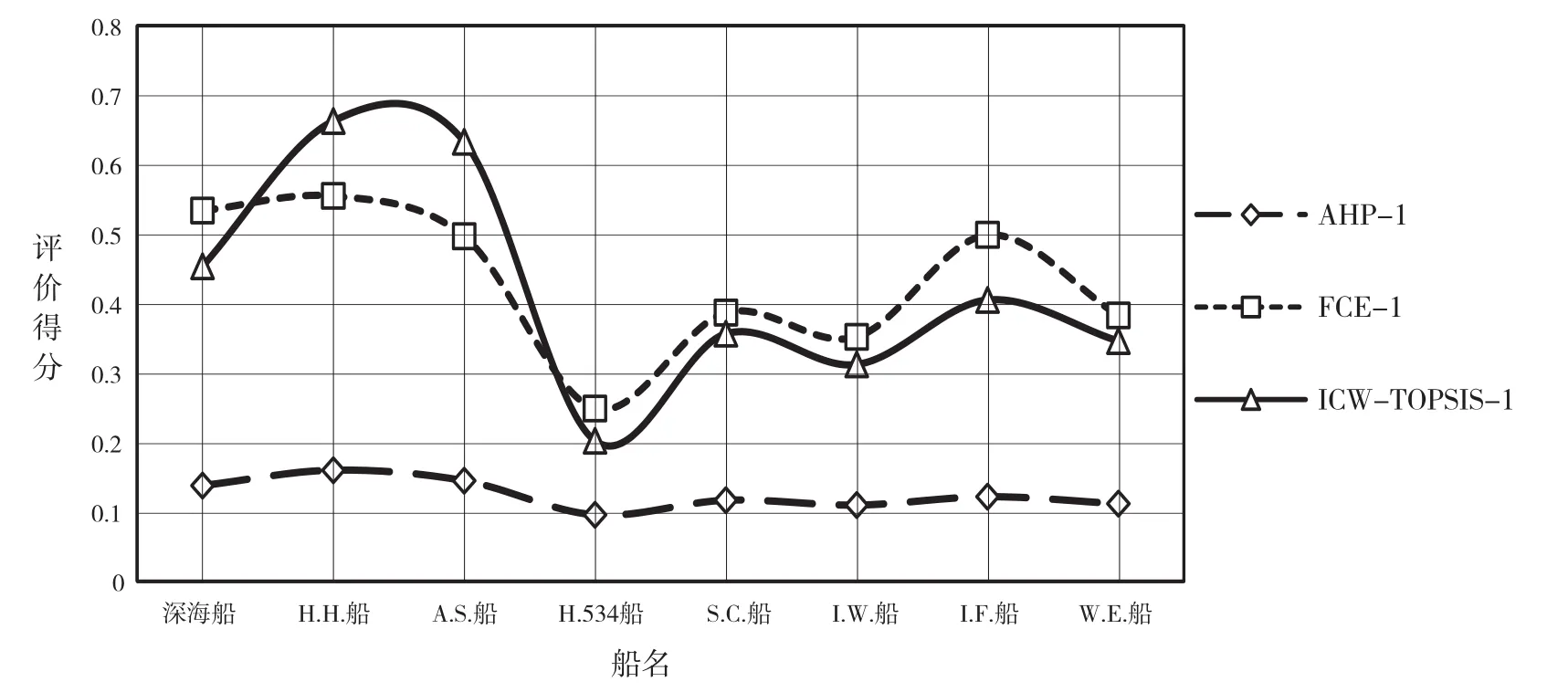
图5 三种评价方法评价得分比较（权重1）

（1）从图5中看出，模糊层次分析法（FCE-1）与改进复合权重TOPSIS（ICW-TOPSIS-1）这两种方法的方案评价得分区分度较大，且得分曲线趋势一致，层次分析法（AHP-1）的方案评价得分曲线趋于平稳，区分度较小。

（2）8艘船的改进复合权重TOPSIS（ICWTOPSIS-1）评价得分与模糊层次分析法（FCE-1）相比，具有较优方案得分更高，较差方案得分更低的特点。

（3）3种方法在同样一组权重系数下，AHP方法与ICW-TOPSIS方法的排序相同；而AHP方法与FCE方法第一、第二、第三方案的排序有变，其余方案排序相同。

6 结 论

经过比较与分析，4种方法中，6组（或5组）权重系数下，各方案排序的趋势基本一致，比较好的船型均为H.H.船、A.S.船，较差的船型均为H.534船，而深海船、I.F.船则在不同方法中排序有变化。具体来说，4种方法的特点如下：

（1）层次分析法：具有计算原理简单，将评价问题分层次的形式使复杂评价问题简单化的优点，适合评价指标数量较多的情况；不过有评价方案得分的区分度小的缺点，不利于方案的决策与取舍，当待评价方案数量较多时，不建议直接使用此方法。

（2）模糊综合评价法：具有指标权重赋值较为灵活的特点，可用来讨论某一指标对方案排序的影响情况，适用于评价指标数量较少的情况；不过，当指标权重改变，方案的得分发生整体性的变化，不利于评价比较，当待评价方案数量较多时，不建议直接使用此方法。

（3）模糊层次分析法：本方法是层次分析法与模糊综合评价法的结合，克服了层次分析法评价得分的区分度小的问题，并且当指标权重改变，方案的得分不会发生整体性变化，即使评价问题的指标、方案较多，此方法也适用。

（4）复合权重TOPSIS：在这四种方法中，该方法的方案评价得分区分度最高，并且本方法中较优方案得分更高，避免出现忽略较优方案的现象；此外，当指标权重改变时，各方案本身得分变化程度最小，有利于方案的决策，适用于方案数量较多的情况。

［ 1 ］ 李劲松，冯恩德. 船型方案的多目标决策——层次分析法［J］. 武汉水运工程学院学报，1993（3）： 295-305.

［ 2 ］ 汪敏，王丽铮. 层次分析法在船型方案选优中的应用［J］. 船海工程，2005（4）： 42-44.

［ 3 ］ 姚雷，李国安，段宏. 层次分析法在大型水面舰船船型多方案优选中的应用［J］. 中国舰船研究，2006（3）：12-14.

［ 4 ］ 刘元丰，唐兴莉. 基于模糊综合评判方法的船舶航行安全评价［J］. 重庆交通学院学报，2004（3）： 123-126.

［ 5 ］ 高丹，寿建敏. 模糊综合评价法在船舶溢油事故定级中的应用［J］. 船舶，2007（4）： 18-21.

［ 6 ］ 黄志，吴兆麟. 船舶条件优劣的模糊综合评价［J］.大连海事大学学报，2001（1）： 9-13.

［ 7 ］ 俎秀花，孟常胜，王涛. 模糊综合评价法在船舶机舱综合评价中的应用［J］. 南通航运职业技术学院学报，2009（4）： 49-52.

［ 8 ］ 周晓洁. 基于模糊综合评价法的船舶热源系统优选研究［D］. 上海交通大学， 2008.

［ 9 ］ 熊云峰，陈章兰，袁红莉. 基于复合权重TOPSIS的船舶性能综合评价法［J］. 船舶工程，2012（3）：28-31.

［10］ 李晓伟，陈红，马娟. 基于AHP复合熵的公路建设项目TOPSIS排序模型［J］. 武汉理工大学学报（交通科学与工程版），2012（5）： 958-961.

［11］ 张爱美，董雅静，吴卫红，等. 基于复合权重-TOPSIS法的我国化工企业环境绩效评价研究［J］. 科技管理研究，2014（18）： 48-52.

［12］ 宋人杰，陈禹名. 基于变权系数的继电保护状态模糊综合评价方法［J］. 电力系统保护与控制， 2016（3）：46-50.

A comparative study of ship technical and economic evaluation methods

ZHANG Ming-xia1JIANG Zhe-lun1XU Xiao-li2
(1.School of Naval Architecture & Ocean Engineering, Dalian University of Technology,
Dalian 116024, China;2.China Shipbuilding Industry Corporation Economic Research Center, Beijing 100120, China)

Ship type selection is a typical problem of multi-objective decision. The traditional evaluation methods,including the analytic hierarchy process(AHP) and the fuzzy comprehensive evaluation(FCE), and the fuzzy analytic hierarchy process(FAHP) derived from the two methods are widely applied in the ship technical and economic evaluation. However, the improved composite weights TOPSIS (ICW-TOPSIS) method is used less in the ship technical and economic evaluation. The paper compares the principle and characteristics of the above four methods to find out their respective advantages and disadvantages according to the evaluation results based on eight work over ships. It provides the relevant suggestions on the selection of the appropriate method for the ship technical and economic evaluation.

analytic hierarchy process(AHP); fuzzy comprehensive evaluation(FCE); fuzzy analytic hierarchy process(FAHP); ICW-TOPSIS; ship technical and economic evaluation

U692.6

A

1001-9855（2017）06-0084-13

10.19423 / j.cnki.31-1561 / u.2017.06.084

2017-06-12；

2017-07-03

张明霞（1969-），女，博士，副教授。研究方向：船舶设计、船舶稳性、海上安全作业智能系统开发、防污染控制技术以及船型技术经

济论证与评价。

姜哲伦（1993-），女,硕士。研究方向：船舶全生命周期理论、船舶技术经济论证。

徐晓丽（1987-），女，工程师。研究方向：海洋工程技术经济分析。