基于应力线性化和主S-N曲线的方形管节点疲劳评估方法
沈秋彬 吴剑国
(浙江工业大学 建筑工程学院 杭州310014)
基于应力线性化和主S-N曲线的方形管节点疲劳评估方法
沈秋彬 吴剑国
(浙江工业大学 建筑工程学院 杭州310014)
通过对美国新奥尔良大学董平沙教授的基于结构应力的主S-N曲线法的介绍,提出了一种基于应力线性化的主S-N曲线法,并给出该方法的操作流程。就方形管节点,分别采用董平沙教授的主S-N曲线法、美国ASME规范中的主S-N曲线法以及文中所述基于应力线性化的主S-N曲线法,进行疲劳寿命评估和比较。通过与热点应力法计算结果进行对比,表明该方法简单易行,且与热点应力法的结果更为接近。
疲劳寿命;主S-N曲线法;结构应力;应力线性化;方形管节点
引 言
管节点在海洋钻井平台中运用比较广泛。其由不同形状和尺寸的空心钢管焊接而成,这些空心管状结构除用于运输石油或天然气外,还支撑着整个平台。 由于管节点不可避免会存在结构几何形状的曲率不连续性以及加工和焊接缺陷,因此造成很大的应力集中,在风、浪、流、冰和潮汐等疲劳载荷作用下,接头高应力区会首先产生表面裂纹,进一步发展将导致节点损坏。
常用的管节点焊接接头疲劳评估方法有名义应力法、局部应力法、热点应力法,其中热点应力法使用比较广泛,并且其计算精度高于名义应力和局部应力法。然而,实际疲劳计算表明,热点应力法尚存在如下缺点:热点应力计算过程比较繁琐;热点应力对网格尺寸和网格划分方式有严格要求;对形状不规则的弧形接头使用不方便;不适用于实体单元。
自2001年起,美国新奥尔良大学董平沙教授及其合作者[1-3]提出一种对网格不敏感的焊接结构疲劳寿命预测方法——主S-N曲线法。 由于该方法对网格尺寸和单元类型均不敏感, 预测的疲劳寿命和失效位置与试验结果又非常一致,因此具有广阔的工程应用前景,现已被ASME规范[4]正式采用。
1 基于等效结构应力和主S-N曲线的疲劳计算方法介绍
鉴于焊接疲劳破坏通常发生在焊趾处,并沿着焊趾在厚度方向扩展,由此可以推断垂直焊线的力及绕焊线的弯矩是张开型裂纹的主要原因[2]。董平沙教授及其合作者首先将有限元计算得到的焊趾处的节点力转化为分布线力;然后基于结构力学基本原理,由线力计算结构应力; 进而在断裂力学框架内给出考虑焊趾缺口、板厚尺寸和加载模式等因素影响的等效结构应力转化方程I(r);最后基于等效结构应力和主S-N曲线即可预测焊趾疲劳寿命。
该方法至今经历了三个发展阶段:第一阶段为董平沙教授在2001年与2002年发表的文献中论述的主 S-N 曲线法(以下简称“P·Dong” 法)[1-2];第二阶段为2007年Fe-safe软件公司和董平沙教授合作开发Verity模块进行疲劳预测;第三阶段为2007年ASME规范对董平沙教授的主S-N曲线法进行修正后编入规范的主S-N曲线法[4]。下文将对P·Dong 法的等效结构应力计算原理以及主S-N曲线法作简要的介绍,其他内容参见相关参考文献。
1.1 结构应力定义
由文献[1]可知,图1中的焊趾处沿板厚方向应力呈非线性分布,该位置总应力其中为薄膜应力为弯曲应力为非线性峰值应力。
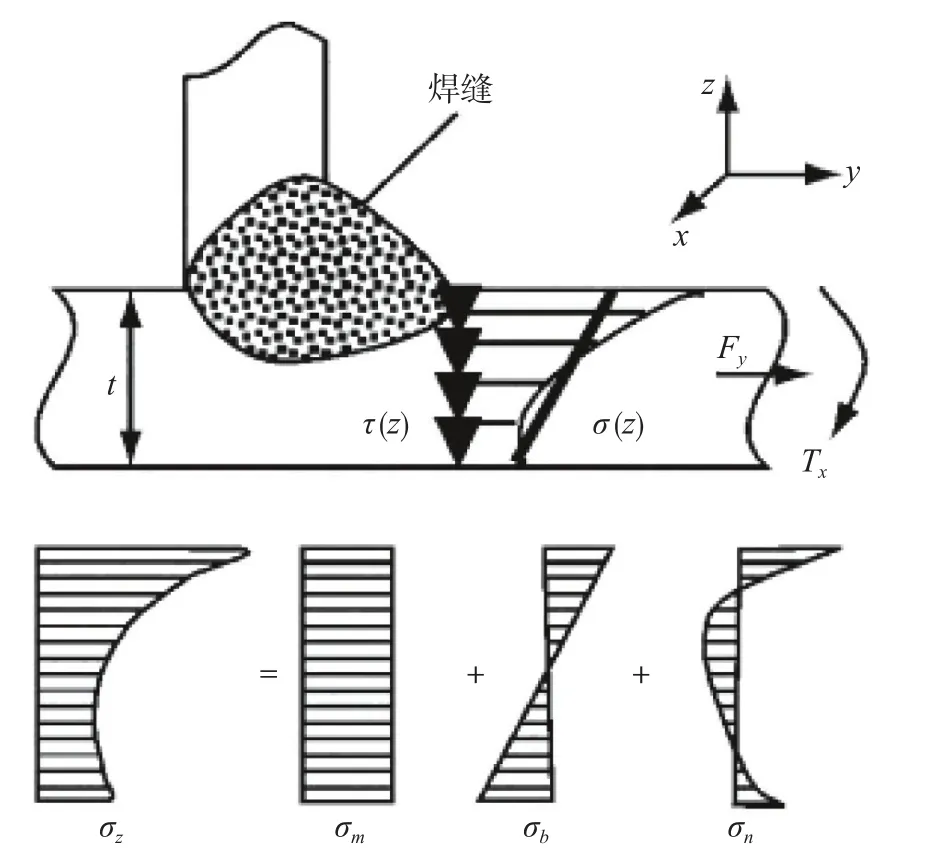
图1 焊趾的应力分布

式中:fy为垂直于焊线方向(x方向)的线力,N;mx为y方向相切与焊线的弯矩,N·mm;t为板厚,mm。
有限元计算时,单元节点力要向边的分布载荷转化,如图2所示。

图2 线力的定义
图2左侧节点1和右侧节点2在y方向的节点力为Fy1和Fy2,绕x方向的节点弯矩为Tx1和Tx2,y方向沿单元边单位厚度的线力在节点1处为fy1,在节点2处为fy2;绕x轴的线力矩在节点1处为mx1,在节点2处为mx2,为x轴向分布的单位厚度线载荷,其表达式见式(2)。


同理,可得到Tx与mx的转换公式,见式(4):

将求得的线力和线力矩带入式(1),从而算得结构应力。
由于结构应力是基于节点力导出的,首先必须从有限元模型中得到焊趾处单元的节点力,如果总体坐标系的y轴未垂直于焊趾,那么还需建立如图2所示的局部坐标系。通过坐标转换得到局部坐标系下的节点力和节点弯矩,然后将节点力转化为相对于厚度中心的线力fx和线力矩my。虽然结构应力对网格不敏感,但是求解过程繁琐[5-6],且计算量相当大,故需要使用特定的计算软件(如Fe-safe软件)。
1.2 基于结构应力的主S-N曲线法
基于结构应力的主S-N曲线法又称“P·Dong法”。在文献[2] 中,董平沙教授导出的等效结构应力见式(5):

P·Dong 法的主S-N曲线可表示为:

式中的参数K和m的值见表1,主S-N曲线如图3所示。
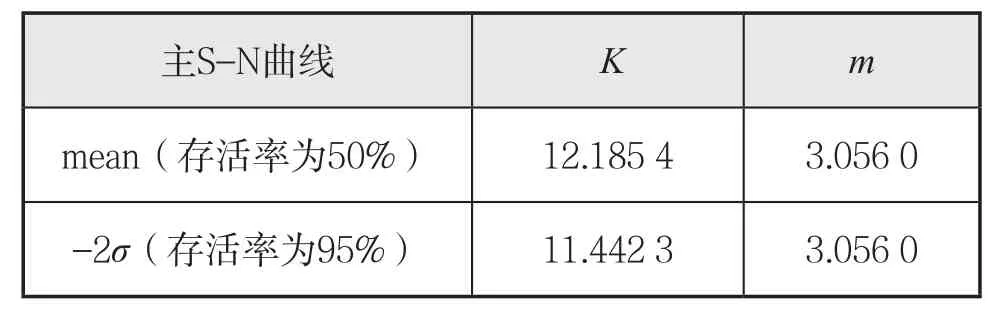
表1 主S-N曲线参数表

图3 主S-N曲线
2 基于应力线性化和主S-N曲线的疲劳计算方法
虽然基于结构应力的主S-N曲线法对网格不敏感,但是求解结构应力比较繁琐,需要使用特定软件求解(如Fe-safe软件中VERITY模块),尤其是采用二次实体单元的模型时,需要在有限元中提取出沿厚度方向的所有节点力,工作量比较大。本文提出以应力线性化方法得到的薄膜和弯曲应力代替结构应力,再结合主S-N曲线进行疲劳寿命计算。
2.1 应力线性化原理
由相关文献[7-8]可知,所谓等效线性化处理就是把计算应力沿厚度分布曲线根据静力等效原理将应力分解成三部分:第一部分是与合力等效且沿截面厚度(或沿应力分类线Stress Classification Line( SCL)[7-8])均匀分布的薄膜应力;第二部分是与合力矩等效且沿截面厚度(或SCL)线性分布的弯曲应力;第三部分是合力和合力矩均为0,且沿截面厚度(或SCL)非线性分布的峰值应力。
沿着厚度截图的应力线性化图解见图4。

图4 沿着厚度截面的应力线性化图解
薄膜应力可以沿壁厚按式(7)计算。根据图4,利用对各类应力的定义,假定单元沿着厚度方向(曲面的外法线方向)为x的正向,现根据静力等效和静弯矩等效,可导出各种分类应力。
薄膜应力:
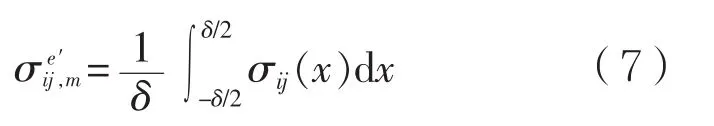
弯曲应力:
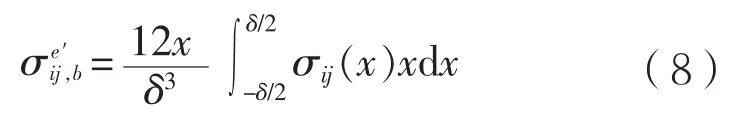
对于实体单元,可以直接通过有限元软件(如ABAQUS、ANSYS)中的使用应力线性化功能来提取薄膜应力和弯曲应力;对于壳单元,只需提取内表面应力和外表面应力,然后由式(9)与式(10)来计算薄膜应力和弯曲应力。

2.2 操作流程
本文在主S-N曲线的基础上,以应力线性化方法得到的薄膜应力和弯曲应力之和代替结构应力,然后使用一条主S-N曲线计算出加载循环次数。操作流程如图5所示。

图5 操作流程图
3 RHS模型与应力计算
3.1 RHS模型介绍
为对基于应力线性化的主S-N曲线法和基于结构应力的主S-N曲线法进行对比,本文建立了如图6所示的方形管节点(Rectangular Hollow Section,RHS)有限元模型,针对计算点(如图7所示),分别计算了结构应力和线性化应力。

图6 有限元模型
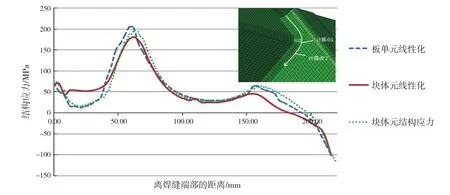
图7 沿焊趾应力分布曲线
现对图6所示模型作如下说明:
(1)模型由101.6 mm×101.6 mm和50.8 mm×152 mm方形截面空心管焊接而成,管长分别为600 mm和364 mm,空心管的壁厚t为7.9 mm。材料弹性模量为210 GPa,泊松比为0.3。把正方形截面管左端通过MPC Beam命令刚性耦合到截面的中心点,在中心点正上方317.5 mm处定义一个参考点并将中心点与参考点刚性耦合,模型接头的另外两端固定在参考点上沿x方向施加17.8 kN的对称交变载荷。
(2)焊缝使用T型单边焊,焊缝倾角为45°,焊脚长度为t。
(3)图6(a)为本文采用的壳单元模型,使用S4R单元进行网格划分,焊缝单元采用S4R单元,厚度为
(4)图6(b)为本文采用的实体单元模型,使用C3D20R单元进行网格划分,沿管壁厚方向分4层,焊缝单元采用C3D15R单元。
3.2 应力计算结果
使用ABAQUS软件对图6中两个模型进行有限元模拟与分析,计算结果见图7,计算点应力汇总见下页表2。

表2 计算点应力汇总MPa
4 基于主S-N曲线的疲劳计算
应用文献[3]、ASME规范中的主S-N曲线法和本文提出的基于应力线性化的主S-N曲线法对图6所示模型进行疲劳计算。为与文献[3]结果进行对比,使用平均主S-N曲线计算点1的循环次数(文献[3]使用平均主S-N曲线,考虑到结果的可比性,对计算点1使用相同的主S-N曲线进行疲劳计算),结果见表3。将表3的结果绘制成图8(a)所示柱状图。

图8 使用应力线性化与结构应力的疲劳计算结果对比
为与热点应力法进行对比,使用-2σ主曲线计算点2的循环次数(热点应力法采用的S-N曲线,其对应的存活概率为 97.6%,所以这里采用存活率为 95%的-2σ主曲线对计算点2进行疲劳计算),结果见表4。同时,运用热点应力法对图6(a)中的计算点2进行疲劳计算,获得计算点处的热点应力范围Δσh=305 N/mm2,修正后的热点应力范围ΔσD=259 N/mm2。使用CCS《船体结构疲劳强度指南》规范中的S-N曲线(D曲线)计算得到循环次数N为87 200。将热点应力结果与表4结果绘制成柱状图,参见图8(b)。
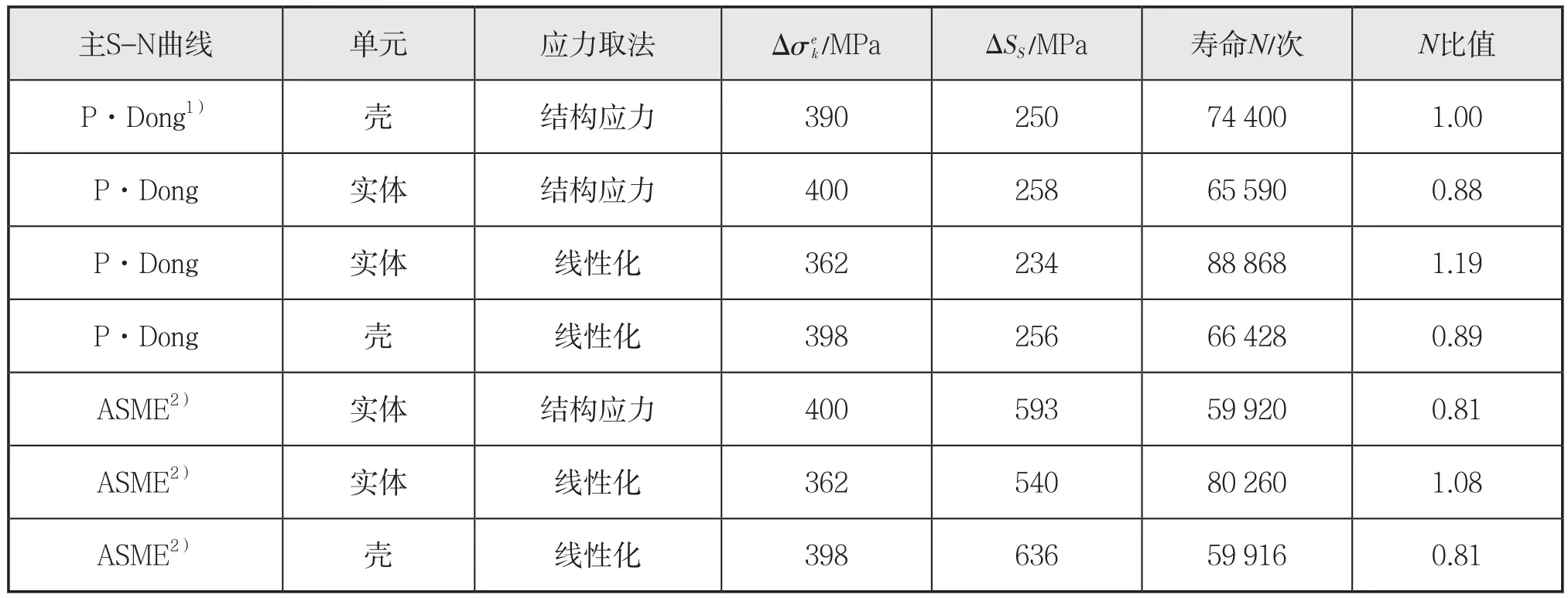
表3 计算点1应力范围与寿命

表4 计算点2应力范围与寿命
5 结 论
通过对整条焊缝焊趾处提取的线性化应力和结构应力对比并且结合图7可知,使用应力线性化计算所得的线性化应力和结构应力吻合较好。
提取两种疲劳计算点的线性化应力和结构应力,分别结合两种主S-N曲线,然后将计算得到的疲劳结果和文献疲劳结果对比,可知:
(1)有限元计算的结果与文献的结果较接近,误差在20%以内。分析产生该误差的原因:一是对于模型焊缝处的网格划分,文献的模型与本文采用的模型存在差别;二是热点应力法中的D曲线和-2σ主曲线的存活率不同,两者相差2.6%。
(2)两种主曲线计算的结果比较接近。
(3)通过图8(b)的比较可知,本文提出的基于应力线性化和主S-N曲线计算出的循环次数与基于热点应力法计算出的循环次数更加接近,所以使用线性化应力代替结构应力简单易行。
综上所述,本文提出的基于应力线性化和主S-N曲线的方形管节点疲劳评估方法是可行的。
[1] DONG P. A structural stress definition and numerical implementation for fatigue analysis of welded joints[J].International Journal of Fatigue,2001(10):865-876.
[2] DONG P,HONG J K,OSAGE D,et a1.Master S-N curve method for fatigue evaluation of welded components[J]. WRC Bulletin,2002(8):474.
[3] HIROKO K, DONG P, Equilibrium-equivalent structural stress approach to fatigue analysis of a rectangular hollow section joint[J]. International Journal of Fatigue, 2005,27; 85-94.
[4] ASME Boiler and Pressure Vessel Committee on Pressure Vessels.ASME VIII division 2-2010 ASME boiler and pressure vessel code[S]. New York: The American Society of Mechanical Engineer, 2010.
[5] 龚琼琼,王成,王效贵. 基于八节点二次壳单元的等效结构应力法[J]. 浙江工业大学学报,2014(5):554-558.
[6] 武奇,邱慧清,郑洋. 基于壳单元的焊接接头的结构应力求解[J]. 焊接学报,2010(7):22-26.
[7] 江楠.压力容器分析设计方法[M].北京:化学工业出版社,2013.
[8] 沈鋆. ASME压力容器分析设计[M].上海:华东理工大学出版社,2014.
Fatigue evaluation of rectangular hollow section joint based on stress linearization and master S-N curve method
SHEN Qiu-bin WU Jian-guo
(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)
A master S-N curve method based on stress linearization and its operation process are presented through the introduction of the main S-N curve method based on the structural stress that was proposed by Professor Dong of University of New Orleans, USA. The fatigue life of a rectangular hollow section (RHS)joint is evaluated and compared by using the master S-N curve method of Professor Dong and ASME rules, as well as the master S-N curve method proposed in the current study. Compared with the hot spot stress method,the master S-N curve method based on stress linearization is simple and practicable with the results closer to the calculations of the hot spot stress method.
fatigue life; master S-N curve method; structural stress; stress linearization; rectangular hollow section(RHS) joint
TG405
A
1001-9855(2017)06-0001-07
10.19423 / j.cnki.31-1561 / u.2017.06.001
2017-08-20;
2017-09-05
沈秋彬(1989-),硕士。研究方向:结构工程分析与设计。
吴剑国(1963-),博士,教授。研究方向:船舶结构分析和设计。

