基于灰关联分析的物流服务失误的评价模型
苏畅 哈尔滨工业大学 徐振中 北京航空航天大学 高瑄 吉林大学 高闻酉 长春理工大学
基于灰关联分析的物流服务失误的评价模型
苏畅 哈尔滨工业大学 徐振中 北京航空航天大学 高瑄 吉林大学 高闻酉 长春理工大学
基于灰关联理论建立物流服务失误的评价模型。首先确定导致物流服务失误的各影响因素,随后对原始数据进行同一量纲处理,利用灰关联分析,计算各因素指标的关联度。
灰关联 服务失误 评价模型
当前物流业已经成长为企业的“第三利润源”,事实上,随着物流业的快速发展,各大物流企业的技术、价格等越来越同质化,在服务失误之后增强自身补救能力已经成为物流企业竞争的优势。
1 构建物流服务失误的评价体系
本文主要用灰关联分析方法计算服务失误的关联度大小,构建物流服务失误的评价模型。
2 灰关联分析的计算方法
A.原始数据转换
均值化处理:设有原数列X,对于任意x(k),k=1,2,3…n,均值化处理得到新数列。
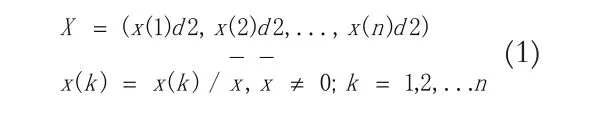
B. 计算关联系数
设灰关联模型的母序列为x0,比较序列为xi,则

计算出下式:

k点x0和xi的绝对差表示为:

两级最小差为:
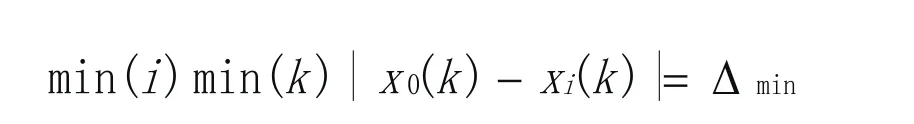
该公式可以拆分为下列两个公式:
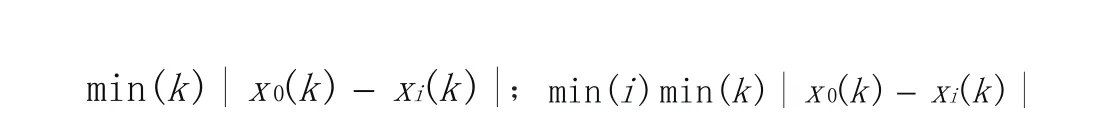
其中前者为第一级最小差,第二个表示为第二级最小差。第二级最大差为:
上述公式中ρ为分辨系数,一般情况下,取值0.5。
C.计算灰关联度
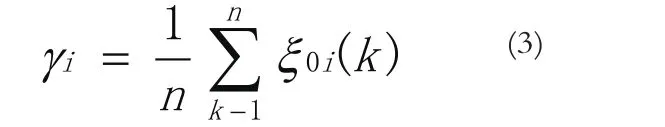
D.排关联序
根据计算得出的关联度排序,可以得出各个因素序列对于母序列的关联程度。
E.列出灰关联矩阵
设有n个母序列{Y1,Y2,Y3….Yn} ,m个因素序列{x1,x2,x3…xm};第m因素序列对于Y的关联度表示为矩阵:

3 案例分析
下面运用上述方法针对于某一物流站点的服务失误进行分析。表1,2是原始数据

表1 顾客对于x物流站点不满意比例 (%)

表2 顾客对于X物流站点不满意的因素比例(%)
3.1 原始数据均值化处理
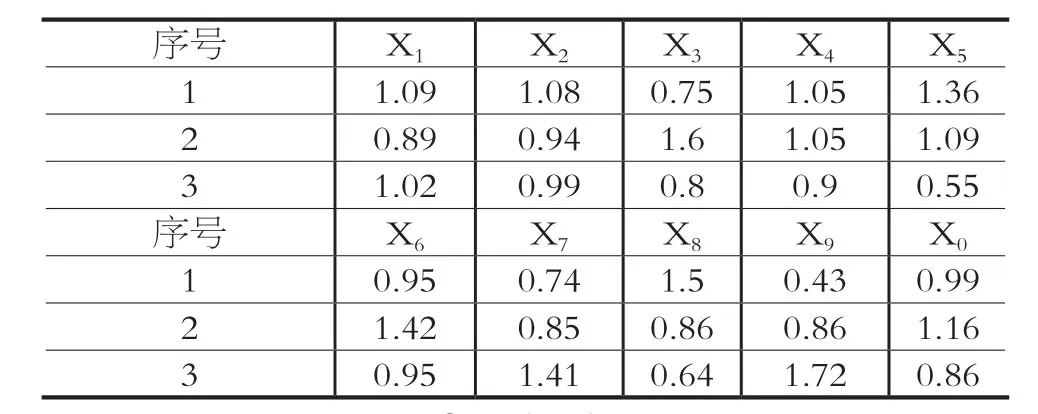
表3 均值变换表
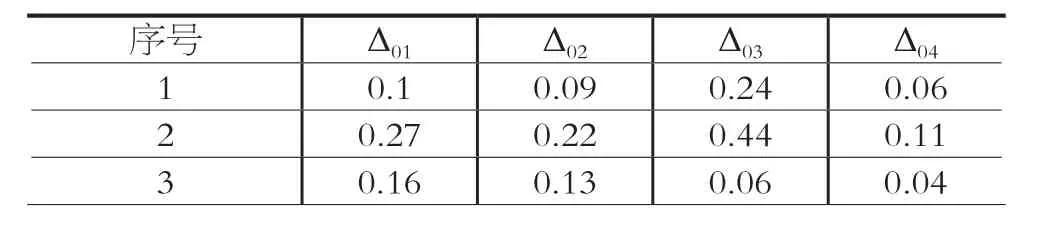
表4 绝对值
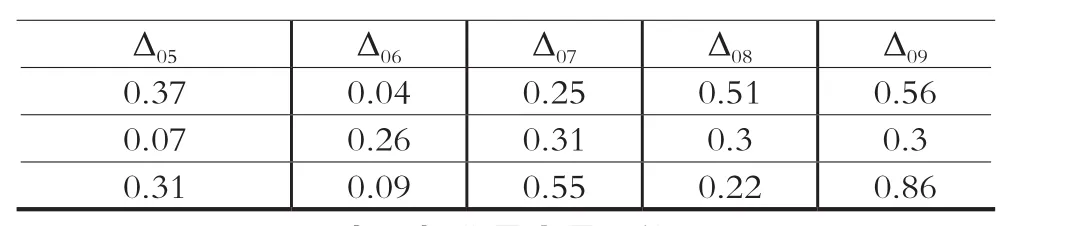
Δ05 Δ06 Δ07 Δ08 Δ09 0.37 0.04 0.25 0.51 0.56 0.07 0.26 0.31 0.3 0.3 0.31 0.09 0.55 0.22 0.86
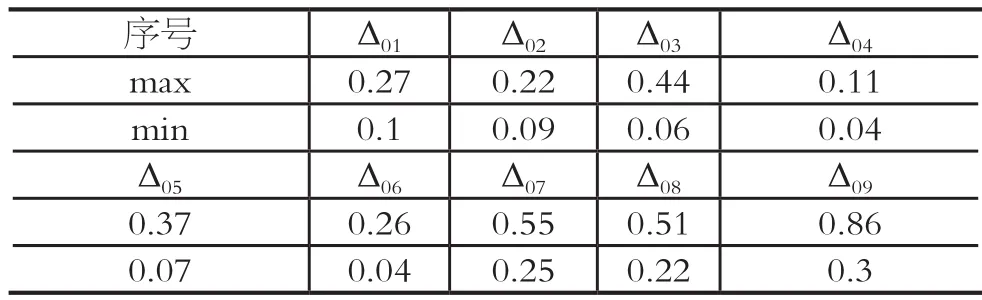
表5 极差最大最小值
3.2 计算关联系数
两级最大值和两级最小值分别为:0.86和0.04,关联度系数结算结果如表6
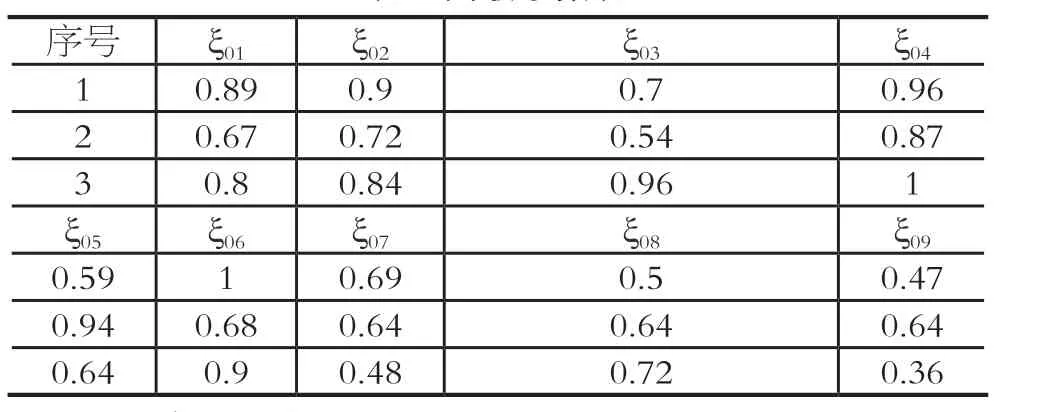
表6 关联系数表
3.3 求关联度
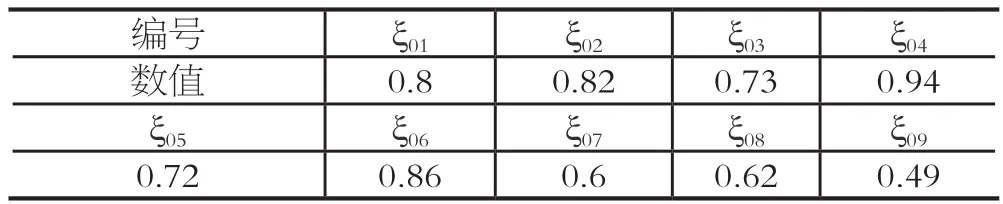
表7 关联度表
3.4 排关联序
根据上表得出的结果,进行关联度排序:
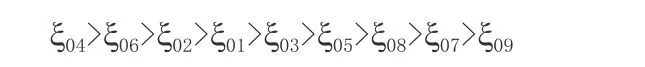
3.5 列关联矩阵
本文的关联矩阵为:(0.8,0.82,0.73,0.94,0.72,0.86,0.6,0.62,0.49)T
4 结论
该文从若干服务失误因素出发,利用灰关联分析建立分析模型,找出导致服务失误最主要的因素,能够很好促进其服务改进。
[1] 魏斐翡.基于网上消费者风险的快递服务满意度分析[J].武汉理工大学学报,2011,33(6):1003-1010.
[2] Sprcng R,Hm'rell D,Mackoy.Service recovery:impact on satisfaction and intentions[J].Joumal of Services Marketing,1995,1:15-23.
苏畅(1995.9—),女,吉林省长春市人,哈尔滨工业大学外语学院英语专业,本科;徐振中(1994.2—), 男,山东临沂, 北京航空航天大学,硕士;高瑄(1993.8—),男,吉林省长春市人,吉林大学超硬材料国家重点实验室,硕士;高闻酉(1968.2—),男,吉林省长春市人,长春理工大学经济与信息管理学院,副教授。

