椭圆中的最值问题归纳
陈国林
(赣南师范大学科技学院 341000)
椭圆中的最值问题归纳
陈国林
(赣南师范大学科技学院 341000)
本文就椭圆中的几类最值问题加以归纳,并举例加以阐述.
椭圆;最值问题;例题
一、知识归纳
1.椭圆过中心的弦中,最长的为A1A2=2a,最短的为B1B2=2b.
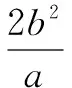
3.椭圆中最大的焦半径为a+c,最小的焦半径为a-c;或者说:椭圆上任一点到焦点的距离的最大值为a+c,最小值为a-c.

4.求一点与椭圆上一点的距离最值问题常用两点距离公式表示,消去x或y转化成二次函数求最值问题.求解时需注意自变量的取值范围.
5.在平面内,设P为一动点,M为定直线l外一定点,d为P到l的距离,d0为M到l的距离,则 |PM|+d的最小值为d0.

6.设A、B是直线l同侧两定点,且直线AB⊥l,点P为直线l上一动点,则∠APB有最大值.
7.设点P为椭圆上任一点,则cos∠F1PF2≥1-2e2,S△F1PF2的最大值为bc.
8.当直线l与椭圆相离时,椭圆上总存在到直线l的距离有最大(小)值的点.
方法1 设P(acosθ,bsinθ),利用点到直线的距离公式——求三角函数的最值;
方法2 设与l平行的直线系l′——与椭圆方程联立消元——令Δ=0——得出与l平行的椭圆的两条切线l1、l2——求出l与l1、l与l2的距离即为所求.
9. 设P为平面内一动点,A、B为两定点,则
(1)|PA|+|PB|≥|AB| 当且仅当点P在线段AB上时取得最小值;
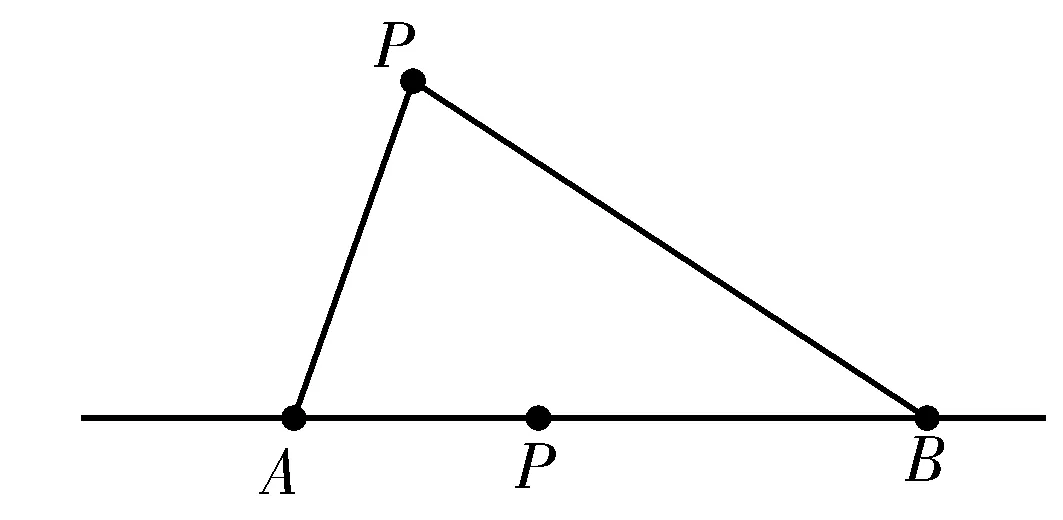
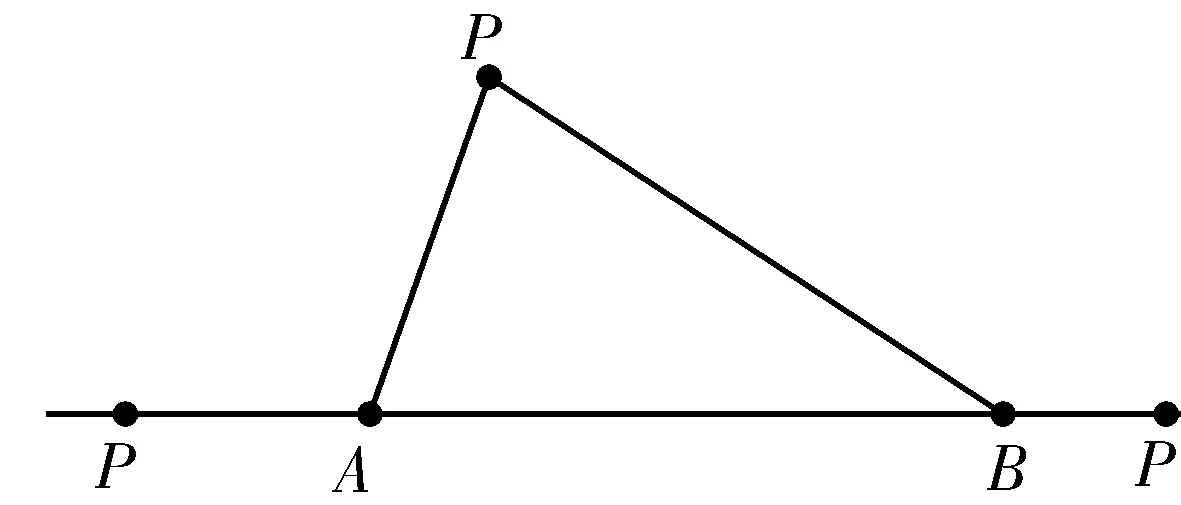
(2) -|AB|≤|PA|-|PB|≤|AB| 当且仅当点P在线段AB(或BA)的延长线时取等号.
10.椭圆上点与一定点距离之和(差)的最值问题往往可用定义转化到另一焦点距离之差(和)进而求解.
二、例题分析





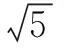



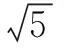

解析由题意知椭圆的两个焦点F1,F2分别是两圆的圆心,且PF1+PF2=10,从而PM+PN的最小值为PF1+PF2-1-2=7.
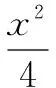
解析设M(x1,y1),N(x2,y2),△F2MN的内切圆半径为r,则



(1)求椭圆E的方程;
(2)当α变化时,讨论线段AD与BC长度之间的关系,并给出证明;
(3)当α变化时,求四边形ABCD面积的最大值及对应的α值.
解析(1)由已知,得b=c=1,所以a2=2.


(2)AD=BC.下面证明:
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),直线AB:x=my-1,则直线DC:x=my+1.





点F2到直线AB:x-my+1=0的距离是

结语椭圆中距离的最值问题一般会从这两点进行考查:①利用椭圆的定义结合平面几何知识求解(适用于所求的表达式中隐含有长轴或者离心率e);②根据椭圆标准方程的特点,把距离问题转化为二次函数求最值的问题(适用于定点在椭圆的对称轴上).
[1]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书( 数学选修2-1)[M]. 北京:人民教育出版社,2008.
G632
A
1008-0333(2017)31-0011-02
2017-07-01
陈国林(1994.12-),男,安徽利辛人,从事数学教育研究.
杨惠民]

