对于解三角形中最值问题的思考

杨冠华

(江苏省金坛第一中学 213200)

对于解三角形中最值问题的思考

杨冠华

(江苏省金坛第一中学 213200)

解三角形日益成为高考的难点和热点，解答时需借助正弦定理、余弦定理、三角形的面积公式，还要熟练掌握三角形的一些平面性质.在高考数学试卷中，作为解答题，解三角形位置相对靠前，难度不是太大，但是当解三角形问题与不等式相结合时，学生常常难以入手.本文结合实例谈一谈三角形最值的求法，并结合三角函数最值，启发学生对数学学习的思考.

三角形；最值问题；解题技巧

问题启发:

那么本题的证明思路已经很清晰了，利用基本不等式，

我们再反过来看这样一个问题，当一个直角三角形面积为定值时，求三角形周长的最小值.已知三角形的三边长分别为a,b,c,且满足a2+b2=c2，设三角形面积为k，k为定值，则三角形的周长l=a+b+c.则由基本不等式：

深入思考：上述两个三角形的最值问题很具有典型性和一般性，但是仅仅解决了关于三角形边的几个基本最值问题.现我们进一步思考这样一个问题，假设我们知道三角形的一条边和一个角，能不能求出三角形周长和面积的最大值.根据三角形边和角的位置关系，我们需要把这个数学问题分成两类：

当角和边相对应时，已知A=θ,A的对边长度为a,求三角形面积和周长的最大值.

y=simBsimC,B+C=π-θ；

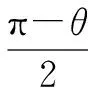
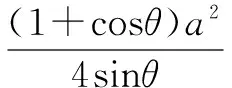
上述从角的角度考虑，运用正弦定理和三角函数解决了面积最大值的问题，如果我们从边的角度出发，同样也可以求出S的最大值.

a2=b2+c2-2bccosθ≥2bc(1-cosθ),

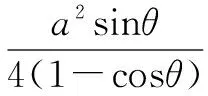
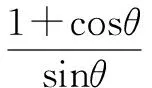
下面我们用类比的方法来解决三角形周长的最大值问题，设三角形的周长为l,则

那么上述问题即转化成求sinB+sinC的最值问题.

记y=sinB+sinC,B+C=π-θ,

y=sinB+sin(B+θ)=(1+cosθ)sinB+cosBsinθ,

y′=(1+cosθ)cosB-sinθsinB.

根据导数的性质，可知当

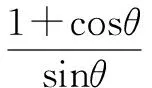
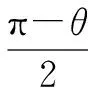
ABC分类法是目前最常用的库存管理方法之一。ABC分类法又称主次因素分析法或“帕累托”现象。这种方法简单易行，在库存管理中应用广泛。ABC分类法的基本原理是将库存物资按品种和占用资金的多少分为特别重要的库存（A类）、一般重要的库存（B类）和不重要的库存（C类）三个等级，然后针对不同重要等级分别进行管理和控制[2]。该方法的核心是“分清主次，抓住重点”，针对企业库存中占用大量资金的少数生鲜农产品，需要进一步加强库存管理和控制；而企业库存中占用少量资金的大多数生鲜农产品，可进行相对较为宽松的库存管理与控制。

此外我们知道sinx其实是一个上凸函数，根据上凸函数的性质我们很容易证明：

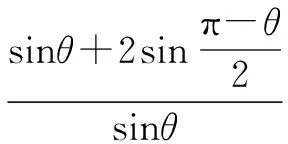
如果我们从边的角度出发，要求l的最大值，其实就是求b+c的最大值.

由余弦定理a2=b2+c2-2bccosθ,进一步对上述整理我们可以得到：

同样我们用上述方法也得到了l的最大值.

当三角形中给的边长和角不对应时，三角形的面积和周长是否依然还存在最大值呢？

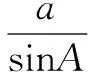
上述表达式在定义域内单调减，所以S不存在最值，因此我们分析得到知道三角形的一条边和一个角不对应时，S不存在最值.

结语：

根据上述研究思路和研究方法，我们也可以类比地得到已知角和边不对应的面积和周长最值的求法，本文就不再深入展开.对于解三角形的最值问题，本文讲述了如何用基本不等式，凸函数以及导数来解决解三角形的最值问题，对于三角形的最值问题还有很多值得我们思考与商榷，笔者也会在以后的学习生活中更加深入地思考.

[1]葛军.新编高中数学竞赛指导[M].南京：南京师范大学出版社，2014:78-79.

G632

A

1008-0333(2017)31-0002-02

2017-07-01

杨冠华(1988.08-)，男，江苏省常州人，硕士，中学二级教师，从事中学数学教学.

杨惠民]