有限群的Engel自同构

常学武,刘亚薇

(山西大学 数学科学学院,太原 030006)

有限群的Engel自同构

常学武,刘亚薇

(山西大学 数学科学学院,太原 030006)

推广了群论中Engel元的定义, 引入了有限群的Engel自同构的概念, 得到了该类自同构的阶与群的方次数的一个精确的整除关系和最佳上界估计,并对有限p-群研究了其Engel自同构集合的若干性质和结构信息, 所得结果不仅加强了Baer定理, 而且可用来研究有限群的自同构及其对群结构的影响.

自同构;Engel元;Engel自同构;Engel次数

0 引言

本文所使用的符号和术语大多是标准的, 可参考群论专著Isaacs[1]和Huppert[2]。

设G为任意群(未必有限), 任取x,y∈G, 记[x,1y]=[x,y]=x-1y-1xy. 一般地, 对任意正整数n≥2, 我们记

[x,ny]=[[x,n-1y],y].

如果对任意x,y∈G均存在正整数n, 使得[x,ny]=1, 则称G为一个Engel群。设g∈G,如果存在正整数n,使得对任意x∈G,都有[x,ng]=1,则称g为G的一个(右)Engel元。

上述Engel条件最先出现在李代数理论中, 如著名的Engel定理:如果一个有限维李代数的每个元素都是ad-幂零的(即Engel元), 则该李代数是幂零李代数。 事实上, 无限Engel群的研究非常活跃, 得到了大量的深刻结果,见文献[3-12]等。 关于有限Engel群,许多学者也进行了深刻的研究, 见文献[13-15]。其中Zorn[2]在1936年证明了一个著名的定理, 即有限Engel群均为幂零群。 Baer[2]得到了两个经典结果, 其一是证明了:如果有限群G可由Engel元生成, 则G幂零;其二是推广了上述Zorn定理, 我们叙述如下,

Baer定理设G为有限群, 则g∈G为Engel元当且仅当g∈F(G)。

其中F(G)表示有限群G的Fitting子群, 即G的唯一极大的幂零正规子群。

[x,nα]=[[x,n-1α],α], ∀x∈G.

如果自同构α也满足类似的Engel条件, 即存在某个正整数n, 使得[x,nα]=1对所有x∈G都成立, 我们称α为G的一个Engel自同构, 而称如此最小的正整数n为α的Engel次数, 简称次数。

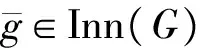
本文首先研究了Engel自同构的次数, 给出了Engel自同构的阶与群的方次数一个精确的整除关系, 并且还得到了最佳的上界估计。 其次探讨了两个Engel自同构的乘积何时还是Engel自同构, 获得了一个有效的充分条件。 最后, 为了得到关于Engel自同构集合更为精确的结构信息, 我们重点考察了有限p-群, 建立了该类群的全体Engel自同构的集合恰为一个群的充要条件。 本文所得的结果, 显示了Engel自同构对群结构有很大的限制和影响,特别是将上述Baer定理推广到自同构, 为深入研究群的结构提供了有用的技术。

1 主要结果及证明

我们先引入Engel自同构的概念。

定义1 设G为有限群,α∈Aut(G), 如果存在一个正整数n使得[G,nα]=1,则称α为G的一个Engel自同构。 称如此最小的正整数n为α的Engel次数, 记为deg(α).

我们记Aute(G)为G的全体Engel自同构组成的集合, 显然G的恒等自同构总是一个Engel自同构。 值得注意的是Aute(G)一般不是乘法封闭的, 从而Aute(G)未必是Aut(G)的子群。

下面是Engel自同构的基本性质, 为此我们需要回顾一个概念。 设α∈Aut(G)为有限群G的一个自同构, 如果存在子群列

G=G0≥G1≥…≥GS=1

使得[Gi,α]≤Gi+1,其中i=0,1,…,s-1,则称α固定该子群列。

引理2 设G为有限群,α∈Aut(G). 则下述等价:

(1)α为G的Engel自同构。

(2)α可固定G的一个子群列。

证明先证明 (1)⟺(2). 假设α为G的Engel自同构, 设deg(α)=n, 根据定义, 可知α固定下述子群列

G≥[G,α]≥[G,α,α]≥…≥[G,nα]=1 .

反之, 如果α可固定G的一个子群列

G=G0≥G1≥…≥GS=1,

按定义即[Gi,α]≤Gi+1, 对任意i=0,1,…,s-1, 据此可推出[G,sα]=1, 表明α为G的Engel自同构。

所以, 我们有

注意到α∈F, 从上述等式可知

按定义, 表明α是G的一个Engel自同构, 即(1)成立。

当α为群G的一个Engel自同构时, 由上述引理知α能固定G的一个子群列。 根据推论4.30[1], 则α的阶o(α)的素因子均整除群G的阶|G|. 本文第一个定理给出了该经典结果的一个加强, 并且得到了最佳上界估计。

定理3 如果α∈Aute(G)且deg(α)=n, 则o(α)|exp(G)n-1, 其中exp(G)为G的方次数, 即G中所有元素的阶的最小公倍数。

证明对deg(α)=n作数学归纳法。 当n=1时, 按定义α为G的恒等自同构, 此时o(α)=1, 结论自然成立。 当n=2时, 按定义有[G,α,α]=1, 下证o(α)|exp(G).

因为[G,α,α]=1, 即对任意的x∈G, 都有[x,α]α=[x,α]. 我们断言[x,αm]=[x,α]m. 下面对m作归纳来证明。 当m=1时, 显然成立。 当m>1时, 由归纳假设, 则

[x,αm]=[x,α·αm-1]=[x,αm-1][x,α]αm-1=[x,α]m-1[x,α]=[x,α]m,

故断言得证。 特别地, 可令m=exp(G), 则[x,αm]=1, 从而o(α)|exp(G)显然成立, 表明所证结论对n=2成立。

下设n≥3.考虑G的长度为n的子群列

G≥[G,α]≥[G,α,α]≥…≥[G,nα]=1.

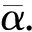
下述例子表明定理3中所给出的上界是最佳的,一般不能再加以改进。

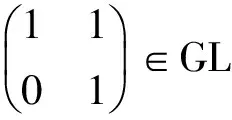
下面我们将研究有限群G的全体Engel自同构的集合Aute(G), 考察其何时也构成一个群,等价于任意两个Engel自同构的乘积仍为Engel自同构。 以下给出一个充分条件。

命题5 设G为有限群, 任取α,β∈Aute(G), 如果αβ=βα, 则αβ仍为Engel自同构。

仍由Baer定理知αβ是G的Engel自同构。

简单计,下面我们将重点讨论G为p-群的情形, 此时有下述关于Engel自同构的简单判据。

定理6 设G为有限p-群, 任取α∈Aut(G), 则α为Engel自同构当且仅当o(α)为p的方幂。

当G=Q8为Hamilton四元数群时,熟知Aut(G)≅S4为四次对称群[10], 由上述定理可知G的Engel自同构等同于阶为2的方幂的自同构,但S4可由对换生成。 该例表明任意群G的两个Engel自同构的乘积一般不是Engel自同构, 即Aute(G)未必成群。 进而, 该例也表明由全部Engel自同构所生成的子群〈Aute(G)〉一般也不是幂零群。

下面给出Engel自同构集合Aute(G)成群的一个充要条件。

定理7 设G为有限p-群, 则Aute(G)是Aut(G)的子群当且仅当Aut(G)的Sylowp-子群正规,即Aut(G)为p-闭群,此时Aute(G)恰为Aut(G)唯一的Sylowp-子群。

证明根据定理6,可知Aute(G)是Aut(G)中所有p-元的集合, 从而等于Aut(G)的所有Sylowp-子群的并,由此推出Aute(G)是一个子群当且仅当Aut(G)的Sylowp-子群是唯一的,即Aut(G)为p-闭群。

一个极端情形是所有的自同构均为Engel自同构,下面给出该现象发生的一个充要条件。

推论8 设G为有限p-群,则Aut(G)=Aute(G)当且仅当Aut(G)仍为p-群。

证明如果Aut(G)=Aute(G),则Aute(G)为群,根据定理7,则Aute(G)恰为Aut(G)唯一的Sylowp-子群,所以Aut(G)为p-群。 反之, 如果Aut(G)为p-群,根据定理6,可知Aut(G)中成员均为Engel自同构,即Aut(G)=Aute(G).

[1] Isaacs I M.Finite Group Theory[M].AMS Providence,Rhode Island，2008.

[2] 胡佩特.有限群论[M].第一卷,第一分册.福州：福建人民出版社,1992.

[3] Golod E S.Some problems of Burnside Type[J].ProcInternatCongrMath,1966,84(2):284-289.

[4] Kappe L C,Kappe W P.On Three-Engel Groups[J].BulletinoftheAustralianMathematicalSociety,1972,7(3):391-405.DOI:10.1017/S000497270004524X.

[5] Macdonald I D,Neumann B H.A Third-Engel 5-group[J].JournaloftheAustralianMathematicalSociety,1967,7(4):555-569.DOI:10.1017/S144678870000450X.

[6] Plotkin B I.Notes on Engel Groups and Engel Elements in Groups.Some Generalizations[Z/OL].arXiv:math/0406100v1 [math.GR],2004.

[7] Bussman C.Commutator Conditions in Normal Closures of Engel Group[D].Saint Louis University,2011.http:∥math.geek-den.net/Bussman-dissertation.pdf.

[8] Khukhro E,Shumyatsky P.Engel-type Subgroups and Length Parameters of Finite Groups[Z/OL].arXiv:1506.00233v2 [math.GR],2015.5

[9] Bacon M R,Kappe L C,Morse R F.On the Nonabelian Tensor square of a 2-Engel Group[J].ArchivderMathematik,1997,69(5):353-364.DOI:10.1007/S000130050133.

[10] 徐明曜.有限群导引(上册)[M].北京:科学出版社,1987.

[11] Shirshov A I.On Some Groups which are Nearly Engel[M]∥Selected Works of A.I. Shirshov. Birkhäuser Basel,2009:137-147.

[12] Mochizuki S B H Y.Third Engel Groups and the Macdonald-Neumann Conjecture[J].BulletinoftheAustralianMathematicalSociety,1971,5(3):379-386.DOI:10.1017/S0004972700047365.

[13] Burns R G,Medvedev Y.A Note on Engel Groups and Local Nilpotence[J].JournaloftheAustralianMathematicalSociety,1998,1(1):92-100.DOI:10.1017/S1446788700001324.

[14] Wilson J S.Two-Generator Conditions for Residually Finite Groups[J].BulletinoftheLondonMathematicalSociety,1991,23(3):239-248.DOI:10.1112/blms/23.3.239.

[15] Bastos R.On Residually Finite Groups with Engel-like Conditions[J].CommunicationsinAlgebra,2016:4177-4184.DOI:10.1080/00927872.2015.1087014.

EngelAutomorphismsofFiniteGroups

CHANG Xuewu,LIU Yawei

(SchoolofMathematicalSciences,ShanxiUniversity,Taiyuan030006,China)

The concept of Engel automorphisms of a finite group is introduced, which generalizes the notion of Engel elements of finite groups. A sharp dividing relationship and a best upper boundary estimation between the order of an Engel automorphism and the exponent of the group are established. Moreover, some properties and structural informations of the set of Engel automorphisms ofp-groups are studied. The results obtained strengthened Baer’s theorem and can be used to study the automorphism groups of finite groups and its influence on the structure of the groups.

automorphism;engel element;engel automorphism;engel degree

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.007

2016-07-27；

2016-12-01

山西省自然科学基金 (201601D011006)

常学武(1984-),男,理学博士,讲师,研究领域为有限群表示论。E-mail:changxuewu@sxu.edu.cn

O152.1

A

0253-2395(2017)04-0721-04