有理Bézier曲线降阶综述

蒋 莉

（湖南农业大学 理学院，湖南 长沙 410128）

有理Bézier曲线降阶综述

蒋 莉

（湖南农业大学 理学院，湖南 长沙 410128）

有理Bézier曲线的降阶是样条曲线和曲面造型中的关键技术之一，为了实现不同CAD系统之间的数据交换，都要用到这一技术，因此它已经成为该领域的热点问题.本文结合作者在该领域的研究成果，综述了近年来国内外专家学者关于有理Bezier曲线的降阶逼近研究的方法、理论成果及实际应用情况，对各种不同的方法进行了分析比较.

有理Bézier曲线；NURBS曲线；齐次坐标；权因子；降阶逼近

1 引言

有理Bézier曲线的降阶逼近问题是指对于给定的一条n阶的有理Bézier曲线，要求我们找到一条m(m＜n)阶的有理Bézier曲线，使其与原曲线的逼近误差达到最小.它经常应用于计算机辅助几何设计的很多方面.比如数据交换，高次曲线曲面的降阶处理，曲线曲面的光顺性研究等.对于这个问题，近年来许多学者都进行了很多研究，提出了一些方法，产生了一些研究成果.覃廉和关履泰[2]提出了基于最优化理论和方法的有理Bézier曲线降阶方法，还将此方法用于NURBS样条曲线曲面的降阶，即将曲线曲面降多阶问题转化为一个二次规划问题来求解.郭清伟，宋颖祥[3]提出了基于广义逆矩阵的有理Bézier曲线一次降多阶逼近的方法.成敏[4]在2003年提出了一种NURBS曲线降阶逼近新算法，该方法利用了已有的NURBs曲线的显式矩阵表示和具有最佳一致逼近性质的chebyshev多项式.周联提出了基于权因子优化的有理Bézier曲线约束降多阶，利用Möbius变换，即重新参数化的方法得到含参数的新的权因子.给出一个方差最小化的目标函数，求解得到参数的值，从而给出了优化的权因子.由于有理Bézier曲线降阶不仅在曲线曲面造型而且在CAD/CAM系统中都有重要的应用，本文总结了几种经典的有理Bézier曲线降阶逼近方法，并分析了各种方法的优缺点.

2 几种有理Bézier曲线的降阶方法

我们首先描述有理Bézier曲线的降阶逼近问题.给定一条n次有理Bézier曲线：

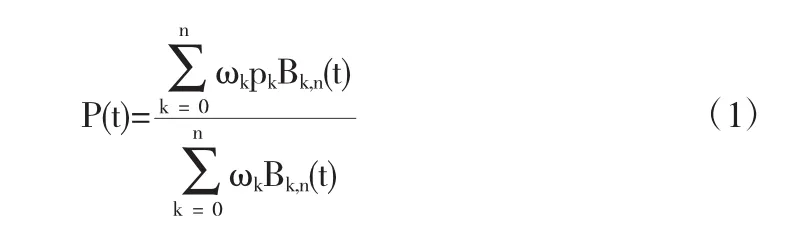
所谓在L2范数下，曲线P(t)作n-m(n＞m)阶降阶逼近，指去寻找一组控制顶点q0,q1,…,qm及相应的权因子γ0,γ1,…,γm，由其确定的m次有理Bézier曲线

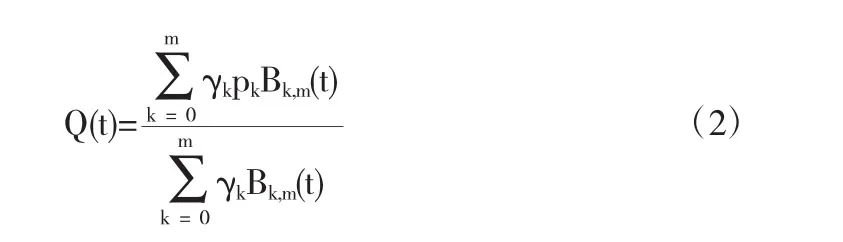
满足条件||P(t)-Q(t)||L2为最小值，

曲线P(t),Q(t)在齐次坐标下的曲线分别是指

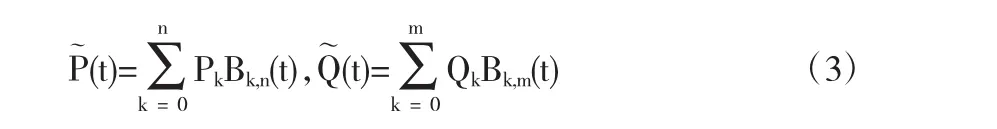
针对上述问题已有如下求解方法.

2.1 将有理Bézier曲线降多阶问题转化为二次规划问题的求解方法

为了解决有理Bézier曲线降阶的非线性规划问题的遗传算法[5]非常费时的问题，覃廉和关履泰将有理Bezier曲线曲面和NURBS曲线曲面放到齐次坐标空间中来讨论[2]，即考虑r次NURBS曲线

其中Nj,r(t)是B样条基函数.利用齐次坐标系，先将f(t)表示成齐次坐标形式然后用 k(k＜r)次 B 样条曲线逼近它.利用齐次坐标，作者将有理Bezier曲线曲面和NURBS曲线曲面的降阶问题转化为如下二次规划问题：

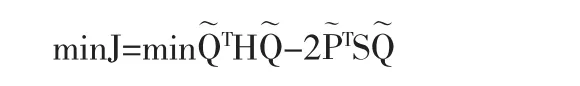
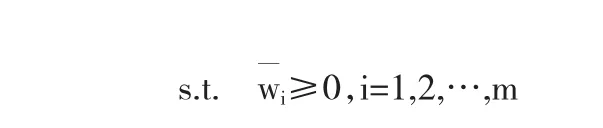
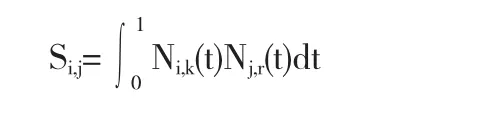
2.2 基于广义逆矩阵的有理Bézier曲线降多阶逼近方法[3]

郭清伟，宋颖祥提出了基于广义逆矩阵的有理Bézier曲线的降多阶逼近方法[3]，该方法完全类似于基于广义逆矩阵的多项式Bézier曲线的降阶逼近的方法，利用了齐次坐标表示，且分别考虑了不保端点插值和保端点高阶插值条件两种情形.假设有一条n次有理Bézier曲线P(t)（见（1））和一条m次有理Bézier曲线Q(t)（见（2）），且Q(t)是P(t)的降阶逼近曲线.利用齐次坐标作者首先把P(t)和Q(t)分别表示成齐次坐标形式应用多项式Bézier曲线的升阶公式n-m次，即逐次将Sm(t)升高，每次升高1阶，直到升高到n次，可得

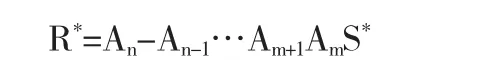
其中S*是升阶前的控制顶点，R*是升阶后的控制顶点，An是n阶升为n+1阶的升阶矩阵，其它Ai类似.将上式简记为：

其中 A=An-An-1…Am+1Am.由于此关系式中的 A(n+1)×(m+1)并非可逆矩阵，但是是一个列满秩矩阵，故利用广义逆矩阵来求解得：

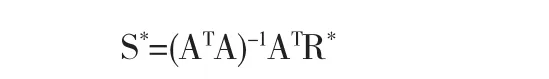
上式是不保端点插值下的一次降n-m阶后的有理m

考虑保端点高阶插值的降阶逼近时，即要求在首末端点处(r,s)(r+s+1＜m+n)阶插值的一次降n-m(n-m≥2)阶，实际上作者是在控制顶点处增加如下条件：

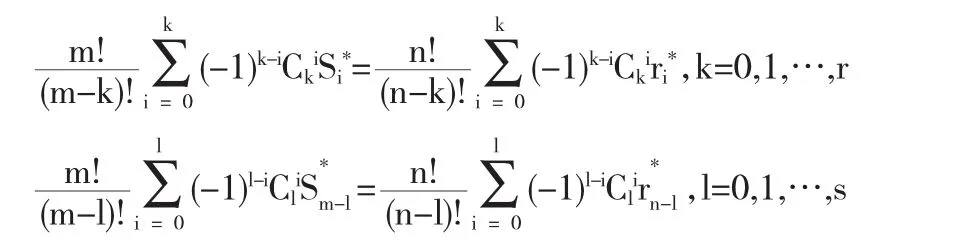
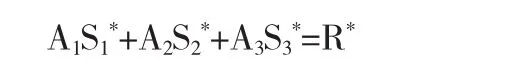
来求得，其中A1和A3分别是A的前面r+1列和后面s+1列，由此解得

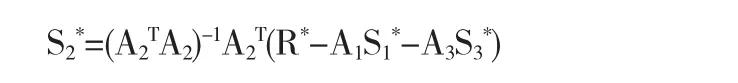
分析和评价：优点是利用升阶的反过程，但因为其矩阵并非方阵，没有逆，故而利用广义逆矩阵，原理比较清晰易懂.给出了显示表达式.存在的问题是采用的是齐次坐标，即在齐次坐标下利用升阶的逆过程来求解得到降阶曲线，但是在仿射坐标系下有本质上的不同，所得到的降阶曲线完全不是严格意义上的升阶的逆.因此也并没有给出降阶后误差函数的界的估计，逼近的效果如何不明显.

2.3 基于权因子优化的有理Bézier曲线的约束降阶

周联首先利用齐次坐标变换和蔡宏杰的结论[6]，得到保端点高阶插值的降多阶的顶点的显式变换公式.

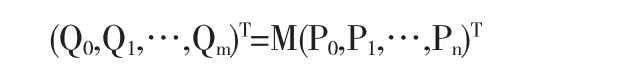
其中Q0,Q1,…,Qm和P0,P1,…,Pn分别是降阶前后的控制顶点，变换矩阵M要经过计算给出.显然，他给出了一个显式的变换公式.接着推导了一个误差上界函数的公式：

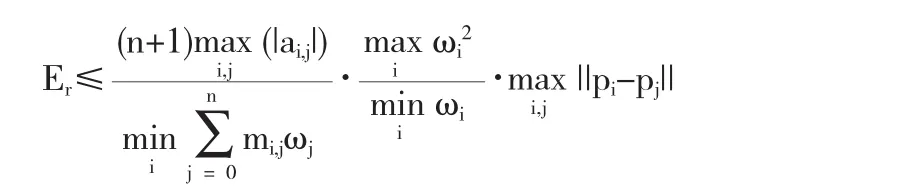
周联在文献[7]中证明了，缩小原曲线权因子之间的比值可以减少降阶误差；而且，利用文献[7]的一种重新参数化的技术，也就是利用Möbius参数变换只改变权因子但不改变控制顶点的性质重新参数化原曲线，得到新的含参数χ的权因子；利用权因子方差最小化建立关于参数χ的一个目标函数，它是一个二次函数，解此最优化问题求出这个合适的参数χ的值.从而实现了原曲线权因子之间的比值缩小的目的.又作者研究出在有些情况下，利用上述方法求出的结果中可能会出现负权因子，所以作者在此目标函数上增加了一个不等式约束，以保证降阶曲线的权因子为正.

分析和评价：该文章的优点是首先利用了已有的一个Bézier曲线的显式降阶算法，该算法在两端点处保任意阶连续，利用的是齐次坐标，原理比较清晰易懂.且给出了显示表达式.然后证明了一个定理，即缩小最大和最小权因子间的比值就能减少误差.利用此定理和Möbius变换，即重新参数化的方法得到含参数的新的权因子，这是因为Möbius变换中有一个自由参数，就利用这个自由参数建立了一个目标函数，使得方差最小化，从而优化最大权因子和最小权因子之间的比值，得到最优参数的值.文章还给出了降阶误差函数的上界的一个表达式，对误差进行了一定的分析和讨论.但是并没有讨论其他参数化方法.

2.4 基于NURBS曲线显式矩阵表示和Chebyshev逼近理论的NURBS曲线降阶逼近[4]

在齐次坐标空间中，成敏利用规范化参数变换将NURBS曲线在非空区间中的一段转换成幂基形式[4].即考虑相应于节点向量T的k阶(k-1次)NURBS曲线：

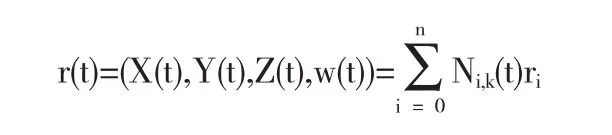
先转换成幂基形式

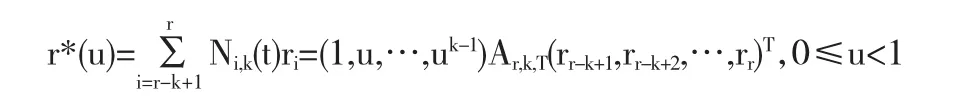
其中系数矩阵Ar,k,T的求解是NURBS曲线表示为幂基形式的一个关键问题.利用广义差商和Marsden恒等式可以求出系数矩阵的两种显示形式.其次，根据可退化即可降一阶的充分必要条件这是一个线性方程组）求出rr-k+1，rr-k+2，…,rr的值.由此推出降阶曲线的表达式为

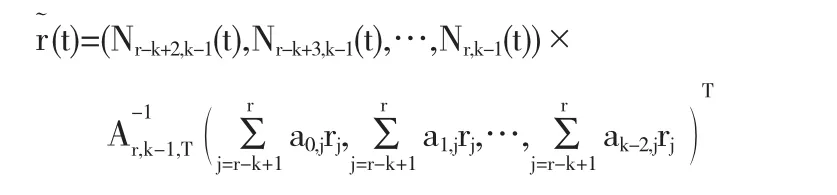
又利用Chebyshev基与Bernsetin基的转换公式推出Chebyshev多项式基Tn(x)=cos(narccosx)与幂基Mn=(1,u,…,un)的线性转换矩阵：

从而将NURBS曲线转化成Chebyshev多项式形式：

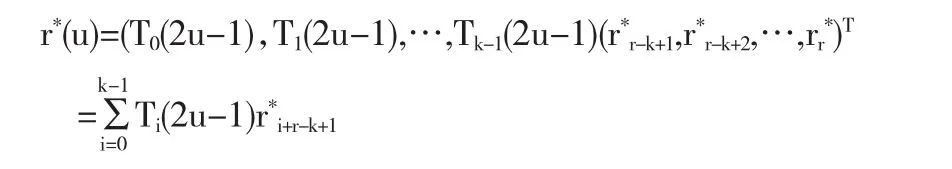
根据已知的Chebyshev多项式的最佳一致逼近性质，得到k-1次曲线最佳一致逼近降阶多项式，即如下k-2次曲线：

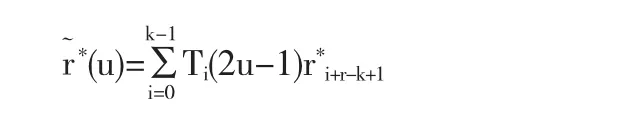
它的特点是系数完全相同，只是减少了一项.

最后再利用前面的公式将它化回NURBS形式：

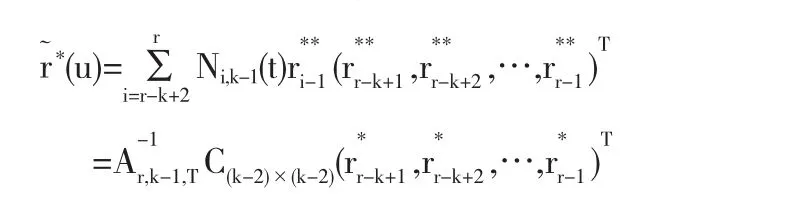
用这种方法一次降多阶就相当于逐次应用降一阶的方法来降阶.算法给出了NURBS降阶逼近曲线的显式表达式，且不需要解方程组，每次降阶都只需要减少一项就可以了.降多阶时就重复其步骤，等价于取曲线在Chebyshev级数表示下的部分和，快速高效，方法独特，计算方便，并且避免了累积误差.类似地利用了它的近似最佳一致逼近性质作者得到了低次的Chebyshev多项式.算法对单区间上的NURBS曲线段有较好的降阶效果，然而对于整条曲线的降阶，作者首先分段处理，然后再对不同段上相同位置的控制点和权因子进行平均，从而得出整条曲线的近似最优降阶逼近曲线.显然，该方法得到的曲线不一定是整条曲线的最优降阶逼近曲线.

2.5 其他有理Bézier曲线的降阶方法

Sederberg和常庚哲在1993年给出了有理平面Bézier曲线的一种降阶方法，利用的是最佳线性公因子，该方法是对没有公因子的多项式组{x(t),y(t),w(t),a≤t≤b}进行一个微小摄动{Xx(t),Xy(t),Xw(t)}，使得扰动后的{x(t)+Xx(t),y(t)+Xy(t),w(t)+Xw(t)}具有有公因子t-T，将问题转化为多变量的管道问题，然后结合Chebyshev多项式进行求解，接着求出有理降阶逼近曲线.但是此方法没有实现在端点处插值.利用移位的Chebyshev多项式，陈发来进行了保端点的摄动，给出了保端点插值的有理曲线降阶逼近方法.康宝生、石茂则把有理曲线的降阶问题转化为求解最优化问题，结合仿生学和遗传算法来实现保端点插值的多次降阶.但是没有显式解，且计算繁琐.

3 结论

鉴于它的实际应用背景，有理平面Bézier曲线的降阶问题已经成为了研究热点，且已经取得了一些研究成果.但这些方法各有弊端，有的可以得到好的降阶效果，有的效果却不明显.本文小结了已有的国内外几乎所有的方法，为将方法推广到B样条曲面和NURBS曲线曲面降阶提供了思路，其中的问题也很多，如齐次坐标下逼近误差与非齐次误差之间的关系研究成果还比较少，需要更进一步地研究.

〔1〕张锐，张彩明.B样条曲线曲面降阶综述[J].工程图学学报，2009(2):1-8.

〔2〕覃廉，关履泰.有理曲线曲面的降阶逼近[J].中国图像图形学报，2006，11(8):1062-1067.

〔3〕郭清伟，宋颖祥.基于广义逆矩阵的有理Bézier曲线降多阶逼近[J].合肥工业大学学报(自然科学版)，2005，28(7):824-828.

〔4〕成敏.基于显式矩阵表示和多项式逼近论的NURBS曲线降多阶[J].中国科学（E 辑），2003，33(8):673-681.

〔5〕康宝生，石茂，张景峤.有理 Bézier曲线的降阶[J].软件学报，2004，15(10):1522-1527.

〔6〕Cai hong-jie WANG-Guo-jin-(Institute-of-Computer-Images-and-Graphics，-State-Key-Laboratory-of-CAD-&-CG，-Zhejiang-University，-Hangzhou-310027，-China).Constrained multi-degree reduction of rational Bézier curves using reparameterization[J].Journal of Zhejiang University(Science A:An International Applied Physics&Engineering Journal)， 2007，8(10):1650-1656.

〔7〕周联.用重新参数化技术改进有理参数曲线曲面的导矢界[J].计算机辅助设计与图形学学报，2010，22(7):1104-1109.

O241.5；TP391

A

1673-260X（2017）12-0001-03

2017-09-22

本文系15年湖南省教育厅科学研究项目“项目名称:有理Bézier曲线曲面的降阶逼近算法及误差分析”(项目编号：15C0656）