基于阻抗特性的六足机器人动态稳定性

艾青林 徐 冬 张立彬

浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州，310014

基于阻抗特性的六足机器人动态稳定性

艾青林 徐 冬 张立彬

浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州，310014

针对六足机器人在崎岖路面行走时，易受到外力干挠发生倾覆失稳的问题，提出一种考虑外力、重心位置、支撑面倾角、运动特性以及机器人阻抗特性的动态稳定性分析方法。建立机器人正运动学和重心求解理论模型，对机器人的实时重心与足端位置进行求解，将机器人绕足端支撑边界的倾翻动作等效为机械旋转系统，在规范化能量稳定裕度判定方法的基础上，建立基于阻抗特性的机器人动态稳定性数学模型，分析不同因素对机器人动态稳定性的影响规律。研究结果表明，机器人阻抗特性极大地提高了机器人的动态稳定性。

六足机器人；动态稳定性；阻抗特性；能量稳定裕度

0 引言

随着机器人技术的发展，机器人在工业、农业、医疗、卫生、娱乐等方面得到了广泛应用[1-2]。目前，机器人结构主要包括串联式、并联式、串并混联式[3]。多足机器人作为串并联机器人，是一个强耦合冗余非线性系统[4]，在行走过程中，机器人自身稳定性是评定机器人性能的一个重要指标[5]。影响机器人稳定性的因素，除了自身结构以外，还包括机器人步行方式、运行速度、外力干扰以及控制误差等[6]。

多足机器人各条腿之间协调动作，实现机器人的步行运动，而步态生成策略则取决于机器人的步行稳定性[7]。目前针对六足机器人在崎岖地面上的动态稳定性，主要采用足力稳定裕度(foot force stability margin,FFSM)[8-9]、零力矩(zero moment point,ZMP)来判定[10]，然而这些判定方法只考虑了机器人的足端反力，考虑因素过少，且不能反映机器人的抗干扰能力。文献[11-12]采用了改善的规范化动态能量稳定裕度(normalized dynamic energy stability margin,NDESM)方法，该方法考虑了机器人运行过程中的惯性力、操作力等，但忽略了机器人的阻抗特性，不能准确地反映机器人抵抗外力冲击的能力。

为了准确地评定机器人运动稳定性与抗干扰能力，本文提出一种考虑自身阻抗特性的六足机器人能量稳定裕度分析方法，并建立了基于阻抗特性的机器人动态稳定性数学模型，分析不同因素对机器人动态稳定性的影响规律，解决了机器人稳定性分析中因忽略外力、外力矩、斜面坡度、运动特性及自身阻抗特性等因素而存在的稳定性判断失误问题，为有效地实现机器人在复杂崎岖地面上动态稳定性控制提供了理论依据。

1 运动学建模

1.1 实验平台

图1所示为六足机器人实验平台，由机身、控制器、电池、传感器以及6条腿组成。在机身上安装了陀螺仪传感器GS-12和红外传感器，可用于检测机身角速度、倾斜程度以及与周围环境距离等；每条腿由3个驱动关节组成，各关节采用高精密伺服舵机Dynamixel RX-24F驱动；机身为正六边形，边长为180 mm，基节长70 mm，股节长150 mm，胫节长135 mm，机器人重4 kg。

图1 六足机器人实验平台Fig.1 The experiment platform of the six-legged robot

1.2 机器人正运动学

根据图1所示的六足机器人平台建立图2所示的六足机器人结构示意图，其中，坐标系ΣO为世界坐标系，与地面固定，坐标系OCxCyCzC与机身固定，坐标原点OC位于机身中心处。

图2 六足机器人结构示意图Fig.2 The structure diagram of the six-legged robot

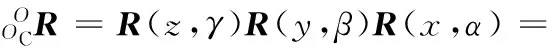
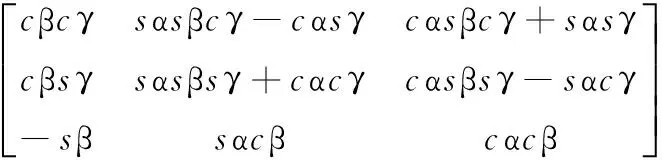
式中，cα=cosα,sα=sinα,cβ、sβ、cγ、sγ依此类推；α、β、γ分别为机器人机身坐标OC在坐标系ΣO下的机身姿态。

图3 机器人单腿D-H模型Fig.3 The D-H model of a leg

已知坐标系原点OC在ΣO中的位置OPC为

式中,vx、vy、vz分别为坐标系原点OC在坐标系ΣO中x、y、z的坐标。

求得两坐标之间的齐次变换矩阵:

(1)

同理可求得各相邻坐标系之间的齐次变换矩阵Mij，则机器人各部分在坐标系ΣO位置坐标可表示为

M0n=M01·M02·…·M(n-1)n

(2)

1.3 实时重心求解

由文献[13]可知，机器人实时重心位置是影响机器人稳定性的重要因素，因此当腿部质量所占比重较大时，进行稳定性分析需考虑腿部质量的影响。为了简便计算，近似求解机器人的实时重心CG，以下推导基于如下假设：机器人各部件均为匀质材料，即各部件的重心均在其几何中心上，如图3所示。

结合式(1)、式(2)求得机器人重心CG_th在坐标系ΣO中的位置坐标：

式中，OCPcg_th为机身重心在坐标系OC中的位置坐标。

根据坐标系之间的齐次变换与运算方法，同理得出，各部件重心在坐标系ΣO中的位置坐标：

把上述各部分质心坐标代入式(3)求得机器人重心在坐标系ΣO的实时位置：

(3)

式中，M为机器人总质量；mcg_th为机身质量；(xO,yO,zO)为机身质点在世界坐标系中的位置；mj、(xj,yj,zj)分别为把所有机器人所有腿共分成n部分时其中一部分的质量，以及质点在世界坐标系中的位置。

在ADAMS中导入六足机器人的三维模型，应用aggregate mass计算工具求得机器人的重心坐标为CG(-1.6918×10-3，-43.2241，1.4772×10-3)mm，在MATLAB中使用式(3)求得机器人的重心坐标为CG(-1.6989×10-3，-43.2242，1.4706×10-3)mm，两者结果相近，验证了式(3)的正确性。

2 机器人的稳定性理论建模

2.1 机器人静态稳定性数学模型

机器人低速步行时，机器人惯性力、角速度等动能对稳定性的影响比较小，为了计算方便，大多数研究一般忽略机器人动能对稳定性的影响，通过采用机器人的静态稳定性判据分析机器人的稳定性。引用文献[14]中所描述的规范化能量稳定裕度NESM(normalized energy stability margin)方法，即机器人实时重心沿各相邻支撑足所组成的支撑边界旋转到支撑边界所在竖直面时重心高度的竖直位移，来分析机器人在斜面上的静态稳定性。该方法考虑了机器人重心位置、斜面坡度，以及支撑足位置对稳定性的影响。根据此方法建立机器人在斜面上的分析图，见图4。

在图4中，CG(XCG，YCG，ZCG)表示机器人的实时重心位置，并设A(xA，yA，zA)、B(xB，yB，zB)为机器人相邻立足点，点O为CG在斜面S上的投影，P(xP，yP，zP)为CG向直线AB作垂线的交点，CG′为CG绕支撑边界AB旋转所能达到的最高点，δi为CG绕支撑边界AB旋转到最高点的旋转角度，φ为斜面坡度，θi为支撑边界与水平面的夹角，E为重心CG向直线PCG′作垂线的交点,fi为各足端所受竖直向上的支撑力。

图4 六足机器人在斜面行走示意图Fig.4 The diagram of the six-legged robot walking on the inclined plane

已知A、B的坐标求得直线AB的表达式为

设

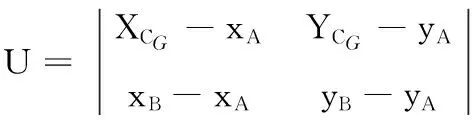
结合上述公式求得CG到直线AB的距离：

(4)

设Z方向的法向量nZ=(0,0,1)，求经过直线AB竖直面ABCG′的法向量nABCG′为

nABCG′=(a,b,c)=lAB×nZ=

(5)

已知P、CG两点坐标，由式(4)、式(5)求得

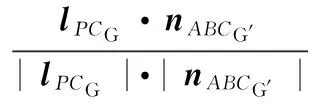
(6)

因此结合式(4)、式(6)求得

D=Hi-hi=Hi-Hicosδi=Hi(1-cosδi)

(7)

式中，D为点E到点CG′的距离；Hi为重心到直线AB的垂直距离；hi为垂足点E到垂足点P的距离。

根据以上公式，同理求得直线AB与地面的夹角θi，且0≤θi≤φ。

结合式(4)，求得以AB为边界的静态稳定程度：

ESNEi=Dcosθi=Hi(1-cosδi)cosθi

(8)

根据稳定裕度的概念，取各相邻支撑边界的稳定程度最小值，即稳定裕度

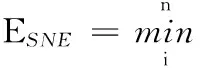
(9)

当ESNE>0时，机器人稳定，且ESNE越大表示其抗外界干扰能力越强。

2.2 基于阻抗特性的动态稳定数学模型

机器人本身作为一种机械装置，在发生摆动或翻转时受到一定的阻抗作用[15-16]，且该特性对机器人的稳定性有一定影响，然而上述稳定性分析方法只考虑了机器人的重心位置，不能完全反映各种干扰因素对机器人稳定性的影响，因此根据上述问题，将六足机器人绕由足端构成的支撑边界的倾翻动作等效为图5所示的机械旋转系统。

图5 六足机器人绕边界等效的机械旋转系统示意图Fig.5 The equivalent diagram of the six-legged robot rotating around the boundary

图5中,KS、C、Ji分别为虚拟扭转刚度的弹性系数、阻尼器的黏性阻尼系数与相对旋转边界的转动惯量。MTi、ωi分别为重心点以支撑边界为转轴的合力矩与角速度,其表达式为

MTi=MTi·eiωi=wi·ei

式中,ei为单位向量，其方向沿支撑多边形的逆时针方向。

(1)根据牛顿第二定律可列出机器人的动力学微分方程：

(10)

(2)结合图4求解机器人绕边界旋转的实时重心处合力矩，即驱动力矩：

式中，MGi为实时重心处重力相对旋转边界产生的力矩；MI为实时重心处的等效惯性力矩；Mri为着地脚因支撑力产生的力矩；ri为各足端到旋转边界的距离。

(3)系数KS、C的测定，由式(10)整理得

(11)

式(11)两边进行拉氏变换，求得其传递函数为

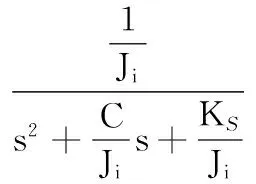
因此求得

(12)

(13)

式中，TC、TS分别为机器人受到一个脉冲力时，机械系统的振动周期与稳定时间；ωn为无阻尼自振角频率。

(4) 求解机器人考虑外力冲击干扰和阻抗的能量稳定裕度。结合式(8)求得机器人绕边界旋转到最高点的势能Ep变化为

设当前时刻重心点以支撑边界i为转轴时的角速度为ωi0，机器人发生翻转时重心点以支撑边界i为转轴旋转到最高点的角速度为ωi1。当ωi0为正时，机器人绕边界旋转到最高点的动能Ek变化为

当ωi0为负时

假设机器人绕边界旋转到最高点时ωi1=0，则机器人在当前位置因外界干扰而不发生完全侧翻所能抵抗的能量为

Ei=Epi-Ep0+Eki-Ek0

求得

(14)

定义能量稳定裕度ESm：

(15)

根据能量稳定裕度的概念可知，ESm越大，表示机器人抗外界干扰能力越强。当ESm>0时，机器人稳定。

3 机器人稳定性分析

为了分析干扰因素对机器人动态稳定性的影响，在ADAMS中建立图6a所示的六足机器人三维模型。初始化条件如下：按机器人实验平台设置各零件尺寸及材料属性，足端与地面之间的静摩擦因数为0.6，动摩擦因数为0.5，机身离地面高度为220 mm，并在关节上添加相应的固定约束与旋转驱动。文中采用典型的三角步态分析机器人的稳定性，三角步态是指将机器人的六条腿分成两组交替使用的步行模式。各关节驱动的初始方向与初始位置设置如图6b所示。图6中，Li(i=1,2,…,6)代表相应的步行腿，Δ135为L1、L3、L5作为支撑腿时，L1、L3、L5足端所形成的支撑面，Δ246为L2、L4、L6作为支撑腿时，L2、L4、L6所形成的支撑面，v为机器人行走方向，图6b中弧形黑色箭头表示旋转驱动的方向。

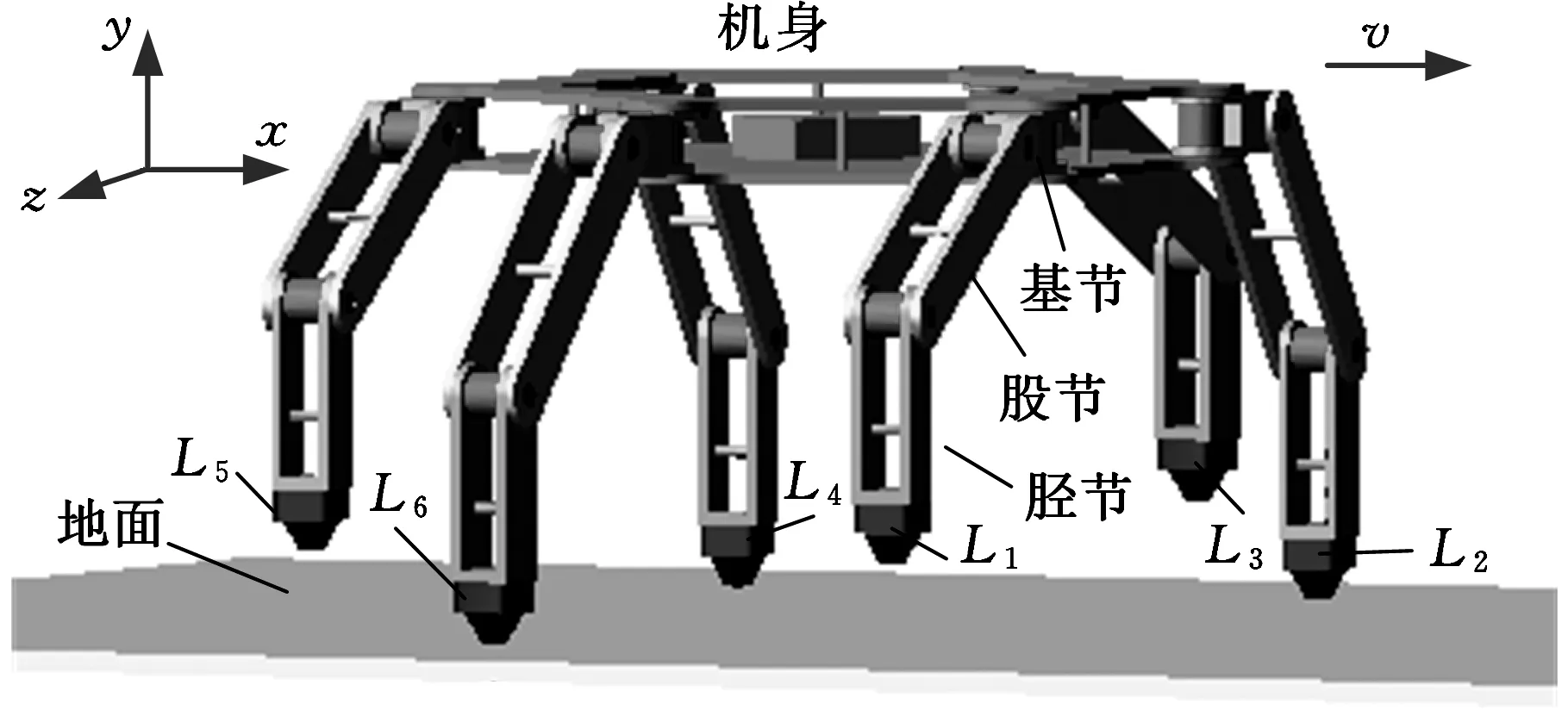
(a)机器人ADAMS三维模型

(b)机器人驱动初始方向与关节初始位置图6 机器人三角步态模型Fig.6 Tripod gait model of the robot

3.1 阻尼系数C、刚度KS的测定

图7所示为机器人模型分别保持三足支撑、四足支撑、五足支撑与六足支撑时支撑足端位置分布。图8为机器人保持上述不同支撑状态下，施加一个脉冲力时，机器人重心在X方向上的振动曲线，由此得到当机器人支撑足数不同时的振动周期TC和稳定时间TS结果如表1所示。

图7 支撑腿足端位置分布Fig.7 Arrangement of supporting legs

从表1中可知，当机器人支撑足数不同时，机器人的振动周期与稳定时间发生改变，即相应的阻尼系数与刚度系数发生变化，因此当机器人采用不同行走步态时需采用相应的阻抗系数进行稳定分析。

(a)三足支撑 (b)四足支撑

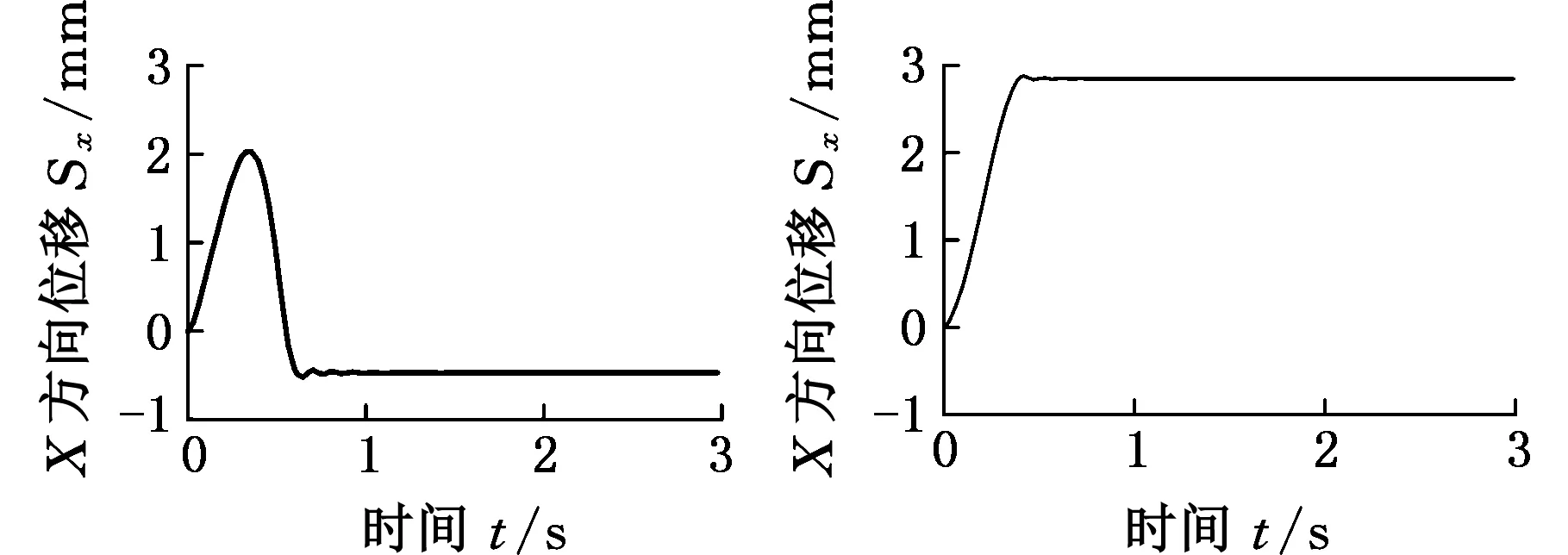
(c)五足支撑 (d)六足支撑图8 机器人在X方向的振荡曲线Fig.8 The curve of the oscillation of the robot in the X direction

三足支撑四足支撑五足支撑六足支撑振动周期TC0.260.240.210.17稳定时间TS1.561.241.050.71

以三足支撑为例，通过MATLAB求解机器人三角支撑面Δ135、Δ246的边界为转轴时所对应的转动惯量：J13=0.213 kg·m2，J15=0.532 kg·m2，J35=0.213 kg·m2；J24=0.532 kg·m2，J26=0.213 kg·m2，J46=0.213 kg·m2。因此据式(12)和式(13)求得：阻尼系数C13=C35=C26=C46=1.0923 N·s/rad，C15=C24=2.7282 N·s/rad，刚度系数KS13=KS35=KS26=KS46=3.1509 N/rad，KS15=KS24=7.8698 N·s/rad。其中Jik、Cik、KSik的下标代表第Li和第Lk支撑足。同理可求机器人处于其他多足支撑时，其支撑边界所对应的转动惯量、阻尼系数与刚度系数。

3.2 稳定性影响因素

以下六足机器人稳定性分析都采用同一三角步态，仿真时间设为13 s，步行时各关节角度的时序图见图9，机器人步态时序图见图10，黑色方框代表支撑时间。

(a)所有腿的偏航关节角度时序图

(b)腿L1、L3、L5的俯仰关节角度时序图

(c)腿L2、L4、L6的俯仰关节角度时序图图9 各关节随时间的角度变化Fig.9 The variation of each joint angle over time

图10 步态时序图Fig.10 The sequence chart of gait

3.2.1足端边界对稳定性的影响

机器人在水平面采用上述步态运动时，支撑面作为支撑相驱动机器人向前运动的过程中，支撑边界相对支撑面不移动，而重心在支撑面的投影随机器人一起前移，即式(8)中对应的δi角发生变化。根据式(8)，机器人各支撑边界的静态稳定程度曲线如图11所示，图中，ESNEik表示由支撑足Li和支撑足Lk组成的支撑边界所对应的静态稳定程度。由图可见，ESNE15和ESNE24远大于ESNE13、ESNE35、ESNE26和ESNE46，即机器人在水平面抵抗同侧边界偏倒的稳定程度远大于对角边界偏倒的稳定程度。其中，机器人足端组成的同侧边界稳定程度平均值比对角边界稳定程度平均值大503.02%。

图11 水平面各足端边界的静态稳定程度(坡度0°)Fig.11 The static stable quantity of boundary of each foot end in the horizontal plane with the gradient of 0°

3.2.2阻抗特性与运动特性对稳定性的影响

当机器人在水平面上行走时，只考虑阻尼和刚度，而忽略实时重心处角速度、力矩及机器人相对支撑边界的转动惯量，则

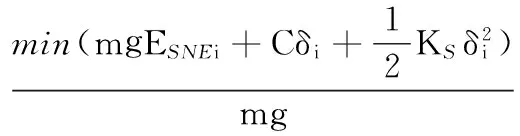
(16)

忽略阻尼和刚度，而考虑实时重心处角速度、力矩及机器人相对支撑边界的转动惯量,则

(17)

根据式(9)、式(16)与式(17)，分别得出机器人不同时刻的静态能量稳定裕度曲线ESNE(点划线)、动态能量稳定裕度曲线ESm1(虚线)和动态能量稳定裕度曲线ESm2(实线)，如图12所示。从图12中可以看出，当机器人整体稳定性只考虑受到刚度和阻尼的影响时，机器人能量稳定裕度值ESm1比静态能量稳定裕度值ESNE大很多，ESm1最小值相比ESNE增大116%，证明机器人的阻抗特性有益于提高机器人的稳定性。

从图12中也可以看出，当不考虑阻尼和刚度时，曲线ESm2在0.2 s、0.8 s、1.2 s、2.3 s等时刻点附近发生明显跳跃， 由于此时刚好为偏航关节旋转驱动的启动或制动时间点，同时腾空足向上运动，导致机器人惯性力矩突然变化，致使机器人稳定性急剧变化。并且ESm2最小值相对静态能量稳定裕度最小值降低了49.57%。

图12 水平面考虑不同因素时的能量稳定裕度(坡度0°)Fig.12 The energy stability margin considering different factors in the horizontal plane with the gradient of 0°

3.2.3斜面坡度对稳定性的影响

根据式(9)和式(15)，分别得出机器人在倾斜角为0°、5°、10°、15°和20°的斜坡上步行时的能量稳定裕度变化曲线如图13所示。

(a)坡度为0°的能量稳定裕度

(b)坡度为5°的能量稳定裕度

(c)坡度为10°的能量稳定裕度

(d)坡度为15°的能量稳定裕度

(e)坡度为20°的能量稳定裕度图13 机器人在不同坡度时的能量稳定裕度Fig.13 Energy stability margin with the different angle of gradient

从图13中可以看出，机器人在步行过程中，机器人能量稳定裕度在一个支撑相周期内波形随坡度改变。取支撑面Δ246为分析对象，令边界26与边界46对应的δi角分别为δ26(t)和δ46(t)，设δ26(t0)和δ46(t0)为支撑相周期起始位置的δi角。由于机器人机身始终与斜面保持平行，因此δ46(t0)随着斜面倾角增大而减小；δ26(t0) 随着斜面倾角增大而增大，如图14所示。

从图13中可以看出，ESm最小值相对ESNE最小值在倾斜角为0°、5°、10°和15°的斜坡上步行时分别增大了90.60%、89.21%、83.27%和41.64%。并且随着坡度的变化，机器人步行时能量稳定裕度发生明显变化；坡度越大时，机器人能量稳定裕度越小。坡度为5°与坡度为0°的ESm最小值相比减小了39.81%；坡度为10°与坡度为0°的ESm最小值相比减小了74.89%；坡度为15°与坡度为0°的ESm最小值相比减小了94.77%。

从图13e中也可以看出，当机器人处于倾斜角为20°的斜坡上步行时，由静态稳定裕度计算得出，ESNE最小值接近于0，表明机器人处于ESNE临界稳定状态；而由动态稳定裕度计算得出，在一些时间段内ESm小于0，表明机器人处于失稳状态，易发生倾覆。而机器人在ADAMS中仿真的结果表明，机器人在20°斜坡上步行时，已经发生了倾覆，如图15所示。因此，证明机器人动态稳定裕度(ESm)计算方法作为机器人稳定性判据的准确性优于常规静态稳定裕度(ESNE)计算方法。

图15 当ESm<0时，机器人发生倾覆动作Fig.15 The tilting action of the robot happened when ESm<0

4 试验与仿真对比

图16为仿真得出的机器人在倾斜角为18.5°的斜坡上步行时的动态能量稳定裕度ESm曲线，可以看出机器人在一些时间段内ESm接近0，说明此时机器人处于临界稳定状态。

图16 坡度为18.5°时的临界稳定状态Fig.16 The critical stable state at the gradient of 18.5°

为了进一步验证机器人动态稳定性评定方法的准确性，对六足机器人进行试验验证。试验中将机器人放在倾斜角度可调的平板上，测试不同坡度对六足机器人运行稳定性的影响。

试验中机器人的初始状态和驱动参数与仿真实验相同，通过试验观察可知，当机器人在18°斜坡上步行时，在0～1 s时间段内，机器人运行稳定，如图17a、图17b、图17c所示，而运行到1.5 s时，L1、L3、L5作为支撑腿，但此时L1发生腾空，机器人发生倾覆现象，如图17d所示。由此可知，试验结果与仿真结果非常接近，证明了动态稳定裕度(ESm)作为机器人稳定性判据的有效性。

5 结论

(1)以六足机器人平台作为研究对象，建立了基于阻抗特性的机器人动态稳定性数学模型，全面地考虑了阻抗、重心位置、外力、惯性力等因素对稳定性的影响。

(a)t=0 (b)t=0.5 s

(c)t=1 s (d)t=1.5 s图17 坡度为18°时的步行试验Fig.17 The walking experiment at the gradient of 18°

(2)机器人在水平面行走过程中，通过对比分析机器人不同支撑边界的稳定程度，得出由足端组成的同侧边界稳定程度远大于对角边界稳定程度。其中，机器人足端组成的同侧边界稳定程度平均值比对角边界稳定程度平均值大503.02%。

(3)建立了基于阻抗特性的能量稳定裕度方程，对机器人进行步行稳定性分析得知，机器人在水平面上考虑基于阻抗特性的能量稳定裕度(ESm)最小值与静态能量稳定裕度(ESNE)最小值相比增大了116%，即机器人自身阻抗有益于改善机器人的稳定性。

(4)对比分析了不同斜面上机器人的动态能量稳定裕度(ESm)，当斜面坡度为5°、10°、15°时，ESm相对水平面时的ESm分别减小了39.81%、74.89%、94.77%，说明坡度越大，机器人运动稳定性越差，机器人稳定性降低得越快。最后通过试验与仿真对比分析，证明了动态稳定裕度(ESm)作为机器人稳定性判据的有效性。

在本文中，对机器人的稳定性进行分析时，未分析非平坦地形、非结构化地形、地面摩擦等因素对稳定性的影响，在后续研究中将分析这些因素对稳定性的影响，优化机器人的行走稳定性。

[1] 谭民, 王硕. 机器人技术研究进展[J]. 自动化学报, 2013, 39(7): 963-972.

TAN Min, WANG Shuo. Research Progress on Robo-tics[J]. Acta Automatica Sinica, 2013, 39(7): 963-972.

[2] 艾青林, 祖顺江, 胥芳. 并联机构运动学与奇异性研究进展[J]. 浙江大学学报(工学版), 2012，46(8): 1345-1359.

AI Qinglin, ZU Shunjiang, XU Fang. Review of Kinematics and Singularity of Parallel Manipulator[J]. Journal of Zhejiang University, 2012，46(8): 1345-1359.

[3] 杨喜飞.混联机器人的类型及其分析[J].科技创新与应用, 2015(21):33-33.

YANG Xifei. Type and Analysis of Hybrid Robot[J].Technology Innovation and Application, 2015(21):33-33.

[4] 陈刚，金波, 陈鹰. 基于速度逆运动学的六足步行机器人位姿闭环控制[J]. 农业机械学报, 2014，45(5):265-270.

CHEN Gang, JIN Bo, CHEN Ying. Position-posture Closed-loop Control of Six-legged Walking Robot Based on Inverse Velocity Kinematics[J]. Transactions of The Chinese Society of Agricultural Machinery, 2014，45(5):265-270.

[5] 夏旭峰, 葛文杰.仿生机器人运动稳定性的研究进展[J]. 机床与液压, 2007, 35(2):229-234.

XIA Xufeng, GE Wenjie.Research Development on Motion Stability of Bionic Robotics[J]. Machine Tool & Hydraulics, 2007, 35(2):229-234.

[6] 柳天虹, 姜树海. 仿生六足机器人稳定性分析与仿真[J].计算机仿真, 2013,30(12): 360-364.

LIU Tianhong, JIANG Shuhai.Stability Analysis and Simulation of Bionic Hexapod Robot[J]. Computer Simulation, 2013,30(12): 360-364.

[7] 王新杰, 李培根, 陈学东,等. 四足步行机器人关节位姿和稳定性研究[J]. 中国机械工程, 2005, 16(17):1561-1566.

WANG Xinjie, Li Peigen, CHEN Xuedong,et al. Research Joint Positions and Robot Stability of an Omnidirectional Crawling Quadruped Robot[J]. China Mechanical Engineering, 2005, 16(17):1561-1566.

[8] AGHELI M, NESTINGER S S. Study of the Foot Force Stability Margin for Multi-legged/Wheeled Robots under Dynamic Situations[C]//IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications. NewYork: IEEE, 2012:99-104.

[9] AGHELI M, NESTINGER S S. Foot Force Criterion For Robot Stability[C]//International Conference on Climbing and Walking Robots and the Support Technologies for Mobile Machines. Clawar, 2012: 417-424.

[10] 刘少智. 旋转足式六足机器人步态及其稳定性研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

LIU Shaozhi. Study on Walking Gait and Stability of the Rotational-legged Hexapod Robot[D]. Harbin: Harbin Engineering University,2012.

[11] GARCIA E, de SANTOS P G. An Improved Energy Stability Margin for Walking Machines Subject to Dynamic Effects[J]. Robotica, 2004, 23(1):13-20.

[12] GARCIA E, GONZALEZ D S P. On the Improvement of Walking Performance in Natural Environments by a Compliant Adaptive Gait[J]. IEEE Transactions on Robotics, 2006, 22(6):1240-1253.

[13] SANDOVAL-CASTRO X Y, CASTILLO-CASTANEDA E,LOZANO-GUZMAN A A. Hexapod Walking Robot CG Analytical Evaluation[J]. International Conference on Intelligent Robotics and Applications, 2014,8917：309-319.

[14] HIROSE S, TSUKAGOSHI H. YONEDA K. Normalized Energy Stability Margin and Its Contour of Walking Vehicles on Rough Terrain[J]. 2001, 1:181-186.

[15] KIM J Y. Dynamic Balance Control Algorithm of a Six-legged Walking Robot, Little Crabster[J]. Journal of Intelligent & Robotic Systems, 2015, 78(1)：47-64.

[16] ZHANG H， LIU Y， ZHAO J, et al. Development of a Bionic Hexapod Robot for Walking on Unstructured Terrain[J]. Journal of Bionic Engineering, 2014, 11(2): 176-187.

HexapodRobotDynamicStabilityBasedonImpedanceCharacteristics

AI Qinglin XU Dong ZHANG Libin

Key Laboratory of E&M,Ministry of Education & Zhejiang Province,Zhejiang University of Technology,Hangzhou,310014

The hexapod robot might be instability when acted by an external force walking on the rough roads. To overcome this problem, a dynamic stability analysis method considering the external forces, the positions of the center of gravity, the dip angles of the bearing surfaces and the impedance characteristics of the robot were introduced. The theoretical model of the forward kinematics and the gravity of the robot were made to calculate the timely gravity centers of the robot and the positions of the footend. In order to simplify the calculation processes, the tip-over motion around the supported line was equivalent to mechanical rotation system. On the basis of the normalized energy stability margin, based on the impedance characteristics the dynamic stability model of the robots was presented to analyze the effect law of the different elements on the dynamic stability of the robots. The results show that the impedance characteristics of the robots improve the dynamic stability of the robots tremendously.

hexapod robot; dynamic stability; impedance characteristic; energy stability margin

2016-12-30

NSFC-浙江两化融合联合基金资助项目(U1509212)；国家自然科学基金资助项目(51275470)；浙江省高等学校中青年学科带头人学术攀登项目(pd2013019)

TP242

10.3969/j.issn.1004-132X.2017.24.014

(编辑王艳丽)

艾青林，男，1976年生。浙江工业大学机械工程学院教授、博士研究生导师。主要研究方向为多足机器人控制技术、钢带并联机器人技术、建筑钢结构探伤机器人技术等。发表论文50余篇。授权专利30余项。E-mail：aqlaql@163.com。徐冬，男，1990年生。浙江工业大学机械工程学院硕士研究生。张立彬，男，1955年生。浙江工业大学机械工程学院教授、博士研究生导师。