障碍物形状对含硫天然气管道泄漏扩散影响的数值模拟

陈 宇， 马贵阳

(辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺 113001)

障碍物形状对含硫天然气管道泄漏扩散影响的数值模拟

陈 宇， 马贵阳

(辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺 113001)

对含硫天然气管道泄漏扩散进行模拟研究，在不同风速下对比分析了计算区域内障碍物形状、障碍物坡度对泄漏气体扩散过程的影响规律，并模拟了不同条件下H2S组分的安全区域。结果表明，障碍物的存在使泄漏气体在风力作用下堆积在障碍物的迎风面，障碍物的形状改变泄漏气体的运动路径。当障碍物为无坡度障碍物(建筑物)时，泄漏气体的扩散高度增大，且在水平方向的传输被阻碍；当障碍物为有坡度障碍物(山体)时，泄漏气体在水平方向的扩散距离增大，且在外界风力达到一定速度之后，泄漏气体绕过障碍物在背风区扩散时开始向下沉降，导致地面附近的安全区域范围减小。减小障碍物坡度，风速较小时对泄漏气体的扩散无影响，风速较大时泄漏气体将障碍物包围并在近地面处扩散；增大障碍物坡度，泄漏气体的扩散规律与无坡度障碍物(建筑物)存在时相似。模拟结果可为含硫天然气泄漏事故的处理提供参考。

含硫天然气； 泄漏扩散； 风速； 障碍物形状； 数值模拟

天然气是一种清洁优质的能源，在优化我国能源结构、改善人民生活环境方面起到重要作用。天然气管道运输具有高效、安全、经济等特点，已成为目前最主要的能源运输方式[1-2]。据统计，我国H2S质量分数大于1%的天然气储量占全国天然气总储量的1/4，已探明的含硫天然气气藏也在逐年增加[3]。在含硫天然气中的强腐蚀性气体H2S对管道内壁的腐蚀作用下，以及管道外壁的老化腐蚀、材料缺陷、第三方破坏、施工缺陷等不可避免的自然和人为因素的影响下，管道泄漏或断裂事故时有发生。泄漏的天然气不仅会造成能源的流失，还会对周围环境和人民生命财产安全造成巨大威胁[4-5]。因此，对天然气管道泄漏扩散进行模拟研究具有重要意义。

国内外的很多学者对天然气管道泄漏扩散进行了模拟研究，得出了一些半经验半理论计算公式[6-8]；李胜利[9]对天然气泄漏扩散进行了三维数值模拟研究，得出了管道架设方式、风速、地形等因素对天然气泄漏扩散的影响规律；朱红钧等[10]利用FLUENT软件对平坦地区含H2S集输管道的泄漏进行了数值模拟，得出了H2S、CH4在平坦地区受风速影响时的扩散规律；于洪喜等[11]对高含硫天然气的泄漏扩散进行了数值模拟，结果表明，高含硫天然气泄漏扩散时近地面的横向污染范围比一般天然气更大，烟云高度有所降低；刘延雷等[12]针对泄漏扩散区的障碍物对天然气泄漏扩散的影响进行了数值模拟，得出了障碍物对天然气泄漏扩散的影响规律。

在实际情况下，天然气管道发生泄漏时泄漏口的位置不确定，如果管道泄漏发生在城镇地区，则周围建筑物对泄漏气体的扩散产生一定影响；如果管道泄漏发生在偏远山区，则山体对泄漏气体的扩散产生一定影响。但是，目前在研究障碍物对天然气管道泄漏扩散的影响时，考虑障碍物形状即障碍物是否存在坡度进行的模拟研究较少。因此，本文模拟高含硫天然气在不同形状障碍物影响下的泄漏扩散过程，分析障碍物形状及风速对H2S、CH4浓度分布及扩散的影响，以期得到不同条件下的安全范围，为管道的安全管理、事故调查及处理提供参考。

1 模型的建立

1.1 数学模型

假定本文所研究的含硫天然气泄漏为连续泄漏，泄漏的H2S、CH4与空气形成混合物，且各组分之间不发生化学反应，混合气体呈湍流流动状态。该研究中所涉及的方程有连续性方程、动量守恒方程、组分方程[13]、标准k-ε方程[14]。

(1)连续性方程：

式中，ρ为密度，kg/m3；uj为j方向的速度，m/s；t为泄漏时间，s。

(2)动量守恒方程：

式中，ui为i方向的速度，m/s；p为作用于流体上的压力，Pa；g为重力加速度，m/s2；Fi为其他体积力，N/m3；μ为动力黏度，Pa·s。

(3)组分方程：

式中，Yi为第i种物质的质量分数；u为传输速度矢量，m/s；Ji为湍流中第i种物质的速率， m/s；Si为由用户自定义而产生的第i种物质的速率，m/s。

(4)标准k-ε方程：

湍流动能方程：

Gk+Gb-ρε-γM+Sk

式中，k为湍流动能，J；xj为j方向传输距离，m；μt为流体的湍流黏度，Pa·s；σk为传输耗散常数，本文取1；ε为湍流耗散率；Gk为平均速度梯度引起的湍动能产生项；Gb为浮力引起的湍动能产生项；γM为可压缩湍流脉动膨胀对总耗散率的影响；Sk为用户自定义条件。

湍流动能耗散方程：

式中，C1、C2、σε为传输耗散常数，本文分别取1.44、1.92、1.3；C12、C3ε为经验常数，本文分别取0.09、0.084 5；Uε=1；Sε为用户自定义条件。

1.2 物理模型及边界条件

本文以某天然气管道为例。天然气输送管道平均压力为3.5 MPa，H2S质量浓度较大，为20 mg/L，外界环境平均温度为18 ℃，天然气的年平均温度为28 ℃；计算区域长为100 m，宽为100 m，该空间足够大且包含泄漏区和扩散区域。假设泄漏口位于该区域底部中间位置，采用二维孔口模型，孔口直径为0.1 m，障碍物位于距泄漏口15 m处，左边为风速入口。

高速气流经由泄漏口喷出，在泄漏口上方一定高度内的速度梯度较大，所以泄漏口附近及上方区域需要网格细划。本文采用非耦合隐式解法，启用组分运输模型而不启用化学反应模型[15]，选取CH4空气混合模型，其中CH4质量分数为95%，H2S质量分数为5%，选取重力和全浮力影响选项。运用湍流强度和水力直径公式计算泄漏口、风速入口、出口处的湍流强度和水力直径，管壁及障碍物壁面设置为固壁，选用Simple算法进行解算。

2 模拟结果及分析

2.1 障碍物无坡度时泄漏气体的扩散规律

假设障碍物宽度为25 m，高度为40 m，距离泄漏口15 m。在计算区域内存在无坡度障碍物时，不同风速下泄漏气体中H2S质量分数分布云图如图1所示。

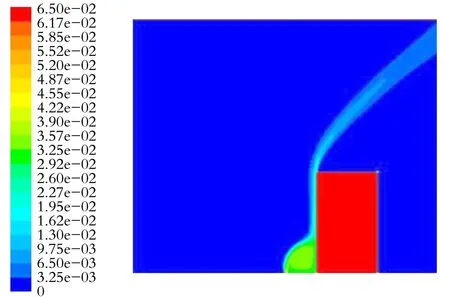
(a) 10 m/s(b) 15 m/s

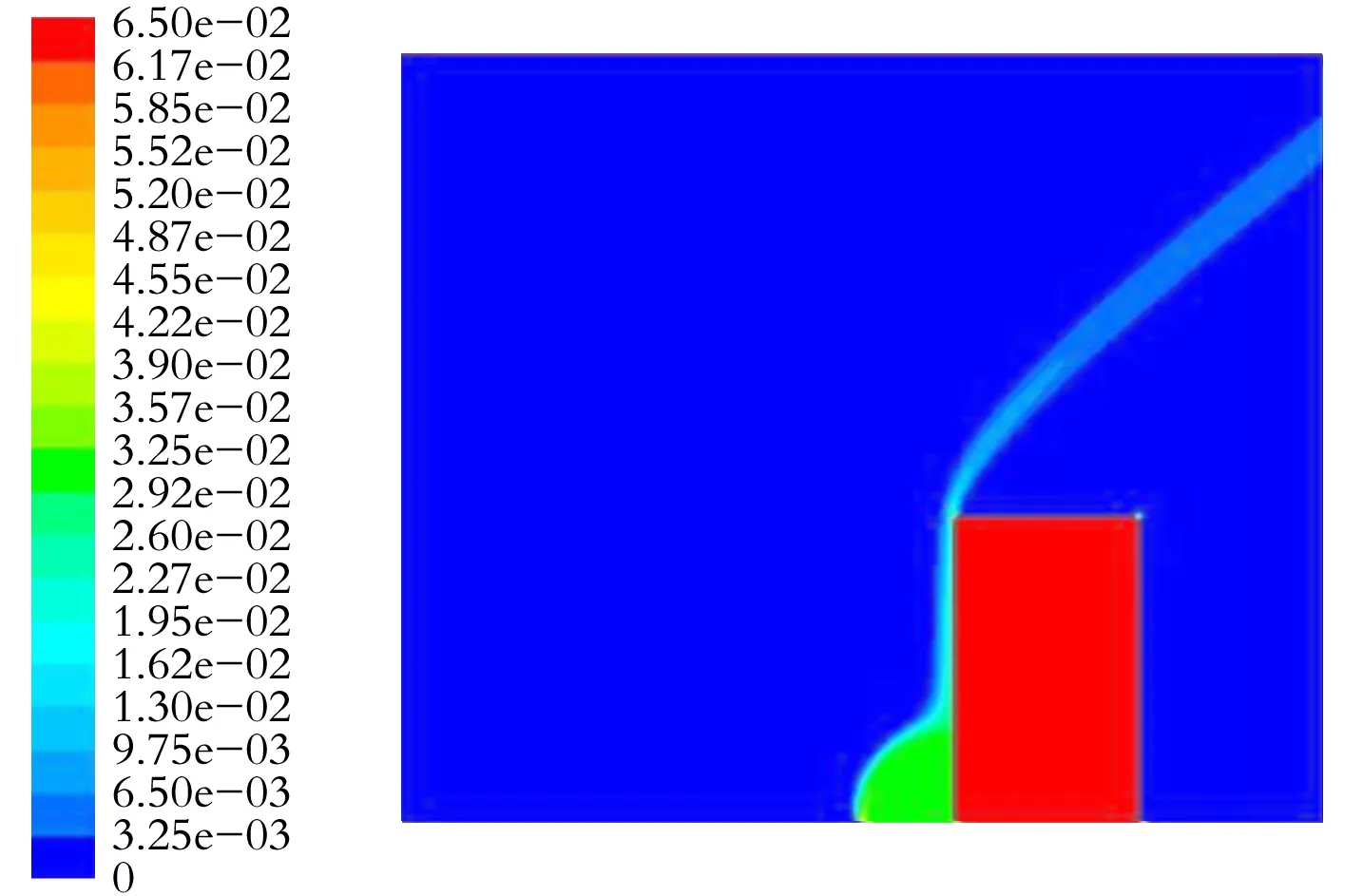
(c) 20 m/s图1 存在无坡度障碍物时不同风速下H2S质量分数分布云图

由图1可以看出，无坡度障碍物的存在增大泄漏气体在竖直方向扩散的高度，阻碍其在水平方向的扩散传输。这是因为：在泄漏初期，泄漏的气体受风力和气体自身重力沉降作用的影响，在靠近地面处扩散，而障碍物的存在阻碍射流气体向下风向倾斜，从而改变泄漏气体的扩散方向和扩散区域。

在水平方向，无坡度建筑物的存在阻碍泄漏气体的横向扩散。泄漏气体在风力作用下有向下风向倾斜的趋势，而当遇到障碍物时，泄漏气体由于无法继续向下风向扩散而堆积在建筑物前，而泄漏口处喷射的气体速度快、浓度大，从而在障碍物前近地面处形成一个高浓度区域，增大该区域的危险性。

在竖直方向，当泄漏气体在扩散过程中遇到无坡度障碍物时，由于障碍物改变大气的流动，使泄漏气体在风力和自身浮力作用的共同影响下沿着障碍物迎风表面垂直向上爬升扩散，从而在障碍物迎风面形成局部较高浓度区，同时也增大气体的扩散高度。随着时间的推移和气体的不断扩散，又由于环境风力加速大气流动，导致泄漏气体被稀释的速度逐渐加快，上升趋势逐渐减弱，随着高度的增加，泄漏气体的浓度逐渐减小。

对比图1(a)、(b)、(c)可以看出，随着风速的增大，泄漏气体在障碍物前的积聚量增大，该区域气体浓度升高。这是由于外界风速越大，泄漏气体向下风向的偏转越明显，使大部分的泄漏气体在近地面处开始扩散，而障碍物阻碍其向水平方向的扩散趋势，从而导致障碍物迎风面泄漏气体浓度更高，该区域的危险性更大。风速越大，越能促进空气的流动，促进泄漏气体的稀释，所以泄漏气体的扩散高度随风速的增大而减小。

2.2 障碍物有坡度时泄漏气体的扩散规律

保持障碍物宽度及泄漏口与障碍物之间的距离不变，将无坡度障碍物改为有坡度障碍物，障碍物高度不变，模拟计算区域内存在有坡度障碍物时不同风速下泄漏气体中H2S的质量分数分布，结果如图2所示。对比图1与图2可以看出，在风力影响下，天然气在有坡度障碍物附近的泄漏扩散与在无坡度障碍物附近的泄漏扩散趋势明显不同。

由图2可知，当障碍物存在坡度时，在泄漏初期，泄漏气体同样会由于风力的作用而积聚在障碍物前表面，使该区域气体浓度升高。但是，由于有坡度障碍物迎风面的倾斜方向与风力的来流方向一致，使泄漏气体扩散方向也沿着障碍物迎风面随障碍物坡度逐渐向下风向偏移，并逐渐向上爬升，导致障碍物迎风面气体浓度较高。当气体运动到障碍物顶端时，速度方向继续随障碍物的坡度而发生改变并逐渐趋于水平，使泄漏气体在外界风力影响下绕过障碍物顶部继续向水平方向扩散，增大在水平方向扩散的距离。

由图2可以看出，当风速小于12 m/s时，H2S气体在空间内的扩散趋势及质量分数分布基本一致；当风速为12 m/s时，绕过有坡度障碍物顶端继续扩散的气体开始有向下沉降的趋势；由图2(d)可以看出，当风速达到15 m/s时，泄漏气体在绕过有坡度障碍物顶端继续扩散一段距离后，向下沉降趋势较为明显；由图2(e)可以看出，当风速继续增大至20 m/s时，泄漏气体在绕过有坡度障碍物顶端后立即开始向地面沉降扩散，且在障碍物背风区浓度分布范围扩大。这是由于有坡度障碍物的存在使其背风面形成一个低压区，风速的不断增大使有坡度障碍物迎风区与背风区的压差不断增大，泄漏气体绕过有坡度障碍物后一部分气体因压差作用而改变速度方向向下运动，导致扩散高度有所降低，在有坡度障碍物背风区的影响范围有所增大。然而，随着泄漏时间的推移，下风向气体的质量分数也逐渐减小，这是由于大气的湍流作用和风力的影响越来越明显，从而加快空气对泄漏气体的稀释。

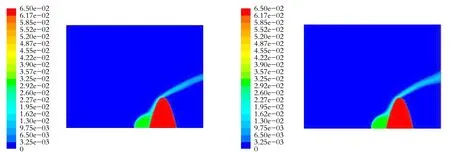
(a) 7 m/s (b) 10 m/s

(c) 12 m/s (d) 15 m/s (e) 20 m/s

图2存在有坡度障碍物时不同风速下H2S质量分数分布云图

2.3 障碍物坡度对泄漏气体扩散的影响

保持障碍物宽度、泄漏口与障碍物之间的距离不变，改变障碍物坡度，模拟了计算区域内存在不同坡度障碍物时不同风速下泄漏气体中H2S质量分数分布，结果如图3所示。

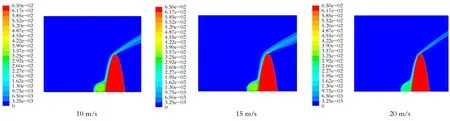
(a) 降低障碍物坡度(障碍物宽度为25 m，高度为20 m)(b) 提高障碍物坡度(障碍物宽度为25 m，高度为50 m)图3 障碍物坡度不同时不同风速下H2S质量分数分布云图

由图3(a)可以看出，当风速较小时，H2S气体在风力和自身重力的共同作用下向下风向偏移并有逐渐向地面扩散的趋势，此时有坡度障碍物对泄漏气体的扩散几乎没有影响，泄漏气体也不会在障碍物前堆积；当风速增至15 m/s时，障碍物对泄漏气体扩散的影响较为明显，泄漏气体会堆积在障碍物迎风面且绕过障碍物后继续沿近地面扩散，气体将整个障碍物包围，增大障碍物附近的危险区域范围，这是由于障碍物坡度较为平缓，高度较低，对气体向下风向自由扩散的阻碍较小。随着风速的继续增大，有坡度障碍物周围的大气流动加快，泄漏气体被稀释的速度也加快，从而使气体在障碍物前的积聚减少，更多气体会绕过障碍物继续扩散，障碍物背风面堆积少部分气体，使障碍物背风面危险区域范围增大。

由图1和图3(b)的对比可得，当有坡度障碍物的坡度较大时，泄漏气体的扩散现象与无坡度障碍物存在时的扩散现象相似。这是由于随着障碍物坡度即陡峭程度的增大，有坡度障碍物的迎风面就越垂直于地面，形状就越接近于无坡度障碍物，因此泄漏气体在其表面扩散时所呈现的现象及规律与图1基本一致。

2.4 含硫天然气泄漏后的安全区域分析

考虑到H2S和CH4的质量分数超过一定范围会对人体和周围环境造成伤害，因此分析含硫天然气泄漏扩散后周围环境的安全区域有重要意义。空气中CH4在标准状态下的爆炸上下限分别为15%、5%(体积分数)，即分别为0.107 55、0.035 85 mg/m3，H2S的质量浓度小于0.000 02 mg/m3才算安全[16]。

无/有坡度障碍物存在时泄漏气体在不同风速下扩散后H2S的安全区域分布云图如图4所示。

(a) 无坡度障碍物

(b) 有坡度障碍物

从图4(a)可以看出，当计算区域内存在无坡度障碍物时，障碍物前表面的气体集聚区域即危险区域几乎不随风速的增大而变化，而沿着障碍物竖直向上的安全区域随风速的增大明显减小。这是因为：风速的增大会加速泄漏气体的扩散，同时空气流动速度的加快也会加速稀释泄漏气体，使空间内的安全区域扩大。由于CH4的安全区域大于H2S的安全区域，因此若要检测在无障碍物影响下含硫天然气泄漏扩散的安全区域，只要检测出H2S的安全区域即可。

由图4(b)可以看出，当计算区域内存在有坡度障碍物时，障碍物前表面的气体集聚区即危险区域几乎不随风速的增大而变化，而当泄漏气体绕过障碍物继续向下风向扩散时，所影响到的范围则有向下增大的趋势，直至近地面处。这是因为：环境风力使有坡度障碍物的背风面形成一个低压区，气流因压差的作用而改变运动方向，导致扩散高度有下降趋势，从而使障碍物背风方向的区域内受泄漏气体影响的区域有所增大且向地面靠近，安全区域范围有所减小。

3 结 论

(1)在外界风力的影响下，障碍物的存在阻碍泄漏气体的扩散，使障碍物迎风面聚集大量泄漏气体，增加该区域危险性；障碍物的形状对含硫天然气管道泄漏扩散有很大影响，无坡度障碍物位于泄漏口下风向时，泄漏气体在竖直方向的扩散高度增大，有坡度障碍物位于泄漏口下风向时，泄漏气体在水平方向的扩散距离增大。

(2)当有坡度障碍物存在时，在风速小于12 m/s情况下，H2S气体在空间内的扩散趋势及质量分数分布基本一致。当风速达到12 m/s时，绕过有坡度障碍物顶端继续扩散的气体开始有向下沉降的趋势；当风速达到15 m/s时，泄漏气体在绕过有坡度障碍物顶端继续扩散一段距离后，向下沉降趋势较为明显；当风速继续增大至20 m/s时，泄漏气体在绕过有坡度障碍物顶端后就开始向地面沉降扩散且在建筑物背风区质量分数分布范围扩大。障碍物的坡度大小对H2S气体的扩散趋势及质量分数分布有很大影响。在降低障碍物坡度的情况下，如果风速较小，则障碍物对气体扩散几乎没有影响；如果风速大于15 m/s，则泄漏气体将障碍物包围，在障碍物迎风区和背风区都会形成高浓度区；在增大障碍物坡度的情况下， H2S气体的扩散趋势及质量分数分布与无坡度障碍物存在时基本一致。

(3)随着风速的增大，泄漏气体在无坡度障碍物附近的水平方向安全范围较大；在有坡度障碍物附近的垂直方向上的安全区域较大，且在障碍物背风区的危险区域随风速的增大而逐渐向近地面处靠近。当有坡度障碍物的坡度降低时，障碍物背风区的危险范围增大；当泄漏口与障碍物之间的距离在一定范围时，泄漏口与障碍物之间的区域均为危险区域且危险较大。分析气体泄漏后受影响区域的安全和危险范围，对应急事故的处理具有一定的指导意义。

[1] 李柯.天然气长输管道泄漏工况数值模拟[J].油气储运，2014，33(1)：20-27.

[2] 雷达.天然气输气管道泄漏事故风险分析[D].北京：北京化工大学，2012.

[3] 潘旭海，蒋军成.化学危险性气体泄漏扩散模拟及其影响因素[J].南京化工大学学报(自然科学版)，2001，23(1)：19-22.

[4] 张琼雅.城镇天然气管道泄漏扩散的CFD模拟及后果分析[D].重庆：重庆大学，2013.

[5] 刘珂，吴明，邵大伟，等.埋地天然气管道泄漏数值模拟[J].石油化工高等学校学报，2012，25(6)：59-62.

[6] 钱新明，冯长根.易燃易爆危险物质泄漏扩散仿真及其应用的研究[J].中国安全科学学报，1997，7(3)：33-36.

[7] Sagrado A P G，Van Beeck J，Rambaud P，et al.Numerical and experimental modelling of pollutant dispersion in a street canyon[J].Journal of Wind Engineering and Industrial Aerodynamics，2002，90(4-5)：321-339.

[8] Berkowicz R.Modelling street canyon pollution：Model requirements and expectations[J].International Journal of Environment and Pollution，1997，8(3-4)：609-619.

[9] 李胜利.复杂地表形态下天然气泄漏扩散的三维数值模拟研究[D].青岛：中国石油大学(华东)，2010.

[10] 朱红钧，林元华，马成学.平坦地区含硫化氢集输管道的泄漏扩散模拟[J].西南石油大学学报(自然科学版)，2009，31(6)：156-160.

[11] 于洪喜，李振林，张建，等.高含硫天然气集输管道泄漏扩散数值模拟[J].中国石油大学学报(自然科学版)，2008(2)：119-122.

[12] 刘延雷，郑津洋，赵永志，等.障碍物对管道天然气泄漏扩散影响的数值模拟[J].石油化工高等学校学报，2007，20(4)：81-84.

[13] 黄雪驰，马贵阳，张一楠，等.风力因素对天然气管道泄漏扩散影响的数值模拟[J].辽宁石油化工大学学报，2015，35(4)：30-35.

[14] 李朝阳，马贵阳，徐柳.架空及埋地天然气管道泄漏扩散数值研究[J].中国安全生产科学技术，2011，7(7)：66-69.

[15] 王亚超，罗振敏，肖旸，等.基于FLUENT的含硫天然气泄漏数值模拟研究[J].西安科技大学学报，2016，36(4)：484-489.

[16] 李刘建.液化石油气管线泄漏事故分析及预防[J].科技资讯，2008，2(4)：58.

Numerical Simulation of Obstacles Shape Influence on Leakage and Diffusion of Sulfurous Gas

Chen Yu， Ma Guiyang

(CollegeofPetroleumEngineering，LiaoningShihuaUniversity，FushunLiaoning113001，China)

The numerical simulation study was performed on the sulfurous gas leakage diffusion. The effects of obstacles shape, slope size of obstacles and the distance between leakage hole and obstacles in the calculation region and different wind speeds on leakage diffusion process were analyzed. The hydrogen sulfide component and methane component safety area were simulated in the different conditions. The results showed that under the action of wind, the presence of obstacles changed the motion path of the gas leakage and led the leakage gas to store in front of its surface. The height of leakage gas diffusion was increased and its transmission in horizontal direction was prevented if the obstacle was no slope obstructions(buildings). The horizontal distance of leakage gas diffusion was increased if the obstacle was gradient obstacles(mountain), and the leakage gas started setting down in the protected area after it bypass obstacles when the wind speed was more than a certain speed, causing the safety area reduced.Reducing obstacles slope, light wind could not influence the diffusion of gas, the leakage of gas was surrounded by obstacles and diffused near the ground when the heavy wind came. Increasing obstacles slope, leakage gas diffusion regularity of slope was similar with no obstructions. The suggestion for emergency rescue and safety management of sulfurous gas leakage accident was provided.

Sulfurous gas； Leakage diffusion； Wind speed； Shape of obstacles； Numerical simulation

1672-6952(2017)06-0019-06

投稿网址：http://journal.lnpu.edu.cn

2106-12-08

2017-03-30

国家自然科学基金项目(41502100)。

陈宇(1993-)，女，硕士研究生，从事天然气管道泄漏方面的研究；E-mail：245268772@qq.com。

马贵阳(1965-)，男，博士，教授，从事计算流体力学及多孔介质传热传质的研究；E-mail：guiyangma1@163.com。

TE88

A

10.3969/j.issn.1672-6952.2017.06.004

(编辑 宋锦玉)